DOCSLIB.ORG

Modeling Destination Choice in Hurricane Evacuation with An

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modeling Destination Choice in Hurricane Evacuation with An Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2005 Modeling destination choice in hurricane evacuation with an intervening opportunity model Bin Chen Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_theses Part of the Civil and Environmental Engineering Commons Recommended Citation Chen, Bin, "Modeling destination choice in hurricane evacuation with an intervening opportunity model" (2005). LSU Master's Theses. 2595. https://digitalcommons.lsu.edu/gradschool_theses/2595 This Thesis is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Master's Theses by an authorized graduate school editor of LSU Digital Commons. For more information, please contact [email protected]. MODELING DESTINATION CHOICE IN HURRICANE EVACUATION WITH AN INTERVENING OPPORTUNITY MODEL A Thesis Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Master of Science in Civil Engineering in The Department of Civil and Environmental Engineering by Bin Chen B.S., Tsinghua University, 2001 May 2005 ACKNOWLEDGEMENTS This paper would not be possible without the help of many people. First and foremost I would like to thank my advisor Dr. Wilmot for his insight and support that contributed immensely to this work. I would also like to thank him for his guidance and encouragement during the difficult time. A special thank goes to Dr. Ishak for his understanding and help. And I also want to thank Dr. Wolshon for his instruction and valuable suggestion. Special gratitude is extended to Professor Earl J. Baker of Florida State University for providing the data on which this research was conducted. My many friends in LSU, including the friends in transportation lab, have made my life here a pleasant journey. In writing this paper, Naveen has given me unselfish help on several occasions. Finally I am thankful for my loving family, my parents and my brother for their endless love and support. ii TABLE OF CONTENTS ACKNOWLEDGEMENTS ........................................................................................ ii LIST OF TABLES........................................................................................................ vi LIST OF FIGURES..................................................................................................... vii ABSTRACT ................................................................................................................... ix CHAPTER 1. INTRODUCTION .............................................................................. 1 1.1 Background .............................................................................................................. 1 1.2 Purpose of Study ...................................................................................................... 2 CHAPTER 2. LITERATURE REVIEW ................................................................. 3 2.1 Hurricanes ................................................................................................................ 3 2.2 Hurricane Floyd ....................................................................................................... 5 2.3 Trip Distribution ...................................................................................................... 6 2.3.1 Destination Choice in Hurricane Evacuation ................................................... 7 2.3.2 Evacuation Modeling Development and State-of–the-art................................ 8 2.4 Intervening Opportunity Model ............................................................................... 9 2.4.1 Formulation .................................................................................................... 10 2.4.2 Application and Evaluation of the Intervening Opportunity Model, Past Experience...................................................................................................... 14 2.4.3 The Similarity of the Gravity Model and Opportunity Model....................... 16 2.4.4 Calibration Method and Model Performance................................................. 17 2.4.5 Goodness-of-fit Measure for Comparison of Geographic Interaction Models ........................................................................................................................ 23 2.4.6 Conclusion...................................................................................................... 24 CHAPTER 3. DATA .................................................................................................. 26 3.1 Survey Data............................................................................................................ 26 3.2 Data Cleaning......................................................................................................... 26 3.3 Separation of the Data............................................................................................ 28 3.4 Geocoding of the Origins and Destinations ........................................................... 28 3.5 Highway Network .................................................................................................. 30 CHAPTER 4. MODELING IN TRANSCAD ENVIRONMENT: BUILDING AN INTERVENING OPPORTUNITY MODEL........................ 31 4.1 Building the Intervening Opportunity Model ........................................................ 31 iii 4.2 Calibrating the IOM ............................................................................................... 31 4.2.1 Building an O-D Matrix from the Data.......................................................... 31 4.2.2 Building an Opportunity Matrix..................................................................... 32 4.2.3 Calibration of IOM in TransCAD .................................................................. 34 4.2.4 IOM Calibration Using Linear Regression .................................................... 35 4.3 Applying the IOM.................................................................................................. 38 4.3.1 Adding Production and Attraction Information ............................................. 38 4.3.2 Apply the distribution model.......................................................................... 39 4.4 IOM Model Performance ....................................................................................... 39 4.4.1 Introduction .................................................................................................... 39 4.4.2 R2 Statistics and Data Comparison................................................................. 39 4.4.3 Trip Length Distribution ................................................................................ 41 CHAPTER 5. THEORETICAL EXTENSION OF THE INTERVENING OPPORTUNITY MODEL ........................................................................................ 45 5.1. Background ........................................................................................................... 45 5.2 A New Extended Opportunity Model .................................................................... 46 5.3 Applying the Extended Opportunity Model in TransCAD.................................... 50 5.3.1 Introduction .................................................................................................... 50 5.3.2 Assumptions of the Coordinate System ......................................................... 50 5.3.3 Linear Transformation on the Coordinates .................................................... 53 5.3.4 Selection of the Shape of the Contour Lines.................................................. 53 5.3.5 Equal Destination Attractiveness Contour ..................................................... 55 5.3.6 Extended IOM Realization in TransCAD ...................................................... 58 CHAPTER 6. COMPARISON OF THREE DIFFERENT MODELS........... 60 6.1 Building a Gravity Model for Comparison............................................................ 60 6.2 Comparison of the Result of the Three Models ..................................................... 60 6.2.1 Average Trip Length ...................................................................................... 60 6.2.2 Coincidence Ratio .......................................................................................... 61 6.2.3 RMSE............................................................................................................. 62 6.2.4 SRMSE........................................................................................................... 62 6.2.5 Information Gain............................................................................................ 63 6.3 Conclusion and Model Comparison....................................................................... 64 CHAPTER 7. SUMMARY AND FUTURE WORK ........................................ 66 7.1 Summary of Model Development.......................................................................... 66 7.2 Summary of Results and Discussion...................................................................... 66 7.3 Opportunities for Future Research......................................................................... 67 REFERENCES ............................................................................................................
Load more

Recommended publications
  • Hurricane & Tropical Storm
    5.8 HURRICANE & TROPICAL STORM SECTION 5.8 HURRICANE AND TROPICAL STORM 5.8.1 HAZARD DESCRIPTION A tropical cyclone is a rotating, organized system of clouds and thunderstorms that originates over tropical or sub-tropical waters and has a closed low-level circulation. Tropical depressions, tropical storms, and hurricanes are all considered tropical cyclones. These storms rotate counterclockwise in the northern hemisphere around the center and are accompanied by heavy rain and strong winds (NOAA, 2013). Almost all tropical storms and hurricanes in the Atlantic basin (which includes the Gulf of Mexico and Caribbean Sea) form between June 1 and November 30 (hurricane season). August and September are peak months for hurricane development. The average wind speeds for tropical storms and hurricanes are listed below: . A tropical depression has a maximum sustained wind speeds of 38 miles per hour (mph) or less . A tropical storm has maximum sustained wind speeds of 39 to 73 mph . A hurricane has maximum sustained wind speeds of 74 mph or higher. In the western North Pacific, hurricanes are called typhoons; similar storms in the Indian Ocean and South Pacific Ocean are called cyclones. A major hurricane has maximum sustained wind speeds of 111 mph or higher (NOAA, 2013). Over a two-year period, the United States coastline is struck by an average of three hurricanes, one of which is classified as a major hurricane. Hurricanes, tropical storms, and tropical depressions may pose a threat to life and property. These storms bring heavy rain, storm surge and flooding (NOAA, 2013). The cooler waters off the coast of New Jersey can serve to diminish the energy of storms that have traveled up the eastern seaboard.
    [Show full text]
  • Verification of a Storm Surge Modeling System for the New York City – Long Island Region
    Verification of a Storm Surge Modeling System for the New York City – Long Island Region A Thesis Presented By Thomas Di Liberto to The Graduate School in Partial Fulfillment of the Requirements for the Degree of Master of Science in Marine and Atmospheric Science Stony Brook University August 2009 Stony Brook University The Graduate School Thomas Di Liberto We, the thesis committee for the above candidate for the Master of Science degree, hereby recommend acceptance of this thesis. Dr. Brian A. Colle, Thesis Advisor Associate Professor School of Marine and Atmospheric Sciences Dr. Malcolm J. Bowman, Thesis Reader Professor School of Marine and Atmospheric Sciences Dr. Edmund K.M. Chang, Thesis Reader Associate Professor School of Marine and Atmospheric Sciences This thesis is accepted by the Graduate School Lawrence Martin Dean of the Graduate School ii Abstract of the Thesis Verification of a Storm Surge Modeling System for the New York City – Long Island Region by Thomas Di Liberto Master of Science in Marine and Atmospheric Science Stony Brook University 2009 Storm surge from tropical cyclones events nor‟ easters can cause significant flooding problems for the New York City (NYC) – Long Island region. However, there have been few studies evaluating the simulated water levels and storm surge during a landfalling hurricane event over NYC-Long Island as well as verifying real-time storm surge forecasting systems for NYC-Long Island over a cool season. Hurricane Gloria was simulated using the Weather Research and Forecasting (WRF) V2.1 model, in which different planetary boundary layer (PBL) and microphysics schemes were used to create an ensemble of hurricane landfalls over Long Island.
    [Show full text]
  • Rev. Rul. 99-13
    Part I. Rulings and Decisions Under the Internal Revenue Code of 1986 Section 42.—Low-Income the United States to warrant assistance by taxable year in which the disaster actually Housing Credit the Federal Government under the Disas- occurred. ter Relief and Emergency Assistance Act, The provisions of § 165(i) apply only The adjusted applicable federal short-term, mid- 42 U.S.C. §§ 5121–5204c (1988 & Supp. to losses that are otherwise deductible term, and long-term rates are set forth for the month V1993) (the Act), the taxpayer may elect under § 165(a). An individual taxpayer of March 1999. See Rev. Rul. 99–11, page 18. to claim a deduction for that loss on the may deduct losses if they are incurred in a taxpayer’s federal income tax return for trade or business, if they are incurred in a transaction entered into for profit, or if Section 165.—Losses the taxable year immediately preceding the taxable year in which the disaster they are casualty losses under § 165(c)(3). 26 CFR 1.165–11: Election in respect of losses occurred. The President has determined that dur- attributable to a disaster. Section 1.165–11(e) of the Income Tax ing 1998 the areas listed below have been Regulations provides that the election to adversely affected by disasters of suffi- Insurance companies; interest rate deduct a disaster loss for the preceding cient severity and magnitude to warrant tables.Prevailing state assumed interest year must be made by filing a return, an assistance by the Federal Government rates are provided for the determination of amended return, or a claim for refund on under the Act.
    [Show full text]
  • Disaster Relief History
    2020 2020 2020 544 Jonesboro, AR. Tornado 20-Mar 543 Tishomingo, MS. Tornado 20-Mar 542 Williamsburg, KY., Jackson, MS, Ridgeland,MS. & Walla Walla, WA. Flooding 20-Feb 542 Nashville, Mt. Juliet, & Cookeville, TN. Tornado 20-Mar 2019 2019 2019 541 Decatur County, TN. Severe Storm 19-Oct 540 Beaumont, Baytown, Orange, & Port Arthur, TX. Flooding 19-Sep 539 New Iberia & Sulphur, LA. Hurricane Barry 19-Jul 538 Dayton, OH. Tornado 19-May 537 Jay, OK. Tornado 19-May 536 Alteimer, Dardanelle, Pine Bluff & Wright, AR; Fort Gbson, Gore & Sand Springs, OK. Flooding 19-May 535 Longview, TX. Tornado 19-May 534 Rusk, TX. Tornado 19-Apr 533 Hamilton, MS. Tornado 19-Apr 532 Bellevue, Fremont, & Nebraska City, NE; Mound City, & St. Joseph, MO. Flooding 19-Mar 531 Savannah, TN Flooding 19-Mar 530 Opelika, & Phenix City, AL; Cataula, & Talbotton, GA Tornado 19-Mar 529 Columbus, MS Tornado 19-Feb 2018 2018 2018 528 Taylorville, IL Tornado 18-Dec 527 Chico, & Paradise (Butte County), CA Wildfire 18-Nov 526 Kingsland, & Marble Falls, TX Flooding 18-Oct 525 Carabelle, Eastpoint, Marianna & Panama City, FL; Blakely, Camilla, Hurricane Michael 18-Oct Dawson, & Donalsonville, GA 524 Sonora, TX Flooding 18-Sep 523 Elizabethtown, Fayetteville, Goldsboro, Grantsboro, Havelock, Jacksonville, Hurricane Florence 18-Sep Laurinburg, Lumberton, Morehead City, New Bern, Riverbend & Wilmington, NC; Dillon, Loris & Marion, SC 522 Shasta County, & Trinity County, CA Wildfires 18-Jul 521 Blanca, Alamosa, & Walsenburg, CO Wildfires 18-Jul 520 Des Moines, & Marshalltown,IA
    [Show full text]
  • Neuse River Basin Regional Hazard Mitigation Plan Table of Contents
    Town of NeuseSunset River Basin Beach RegionalUnifiedDRAFT HazardDevelopment Mitigation Ordinance Plan Greene, Jones, Lenoir, Pitt and Wayne Counties Draft: January 9, 2015 NEUSE RIVER BASIN REGIONAL HAZARD MITIGATION PLAN TABLE OF CONTENTS PAGE SECTION 1. INTRODUCTION & PLANNING PROCESS I. INTRODUCTION.. 1-1 II. NEUSE RIVER BASIN REGION. 1-1 III. HAZARD MITIGATION LEGISLATION.. 1-2 IV. WHAT IS HAZARD MITIGATION AND WHY IS IT IMPORTANT TO THE NEUSE RIVER BASIN REGION?. 1-3 A. What is Hazard Mitigation?. 1-3 B. Why is Hazard Mitigation Important to the Neuse River Basin Region?. 1-3 V. PLAN FORMAT . 1-4 VI. INCORPORATION OF EXISTING PLANS, STUDIES, AND REPORTS. 1-6 VII. PLANNING PROCESS .. 1-6 VIII. AUTHORITY FOR HMP ADOPTION AND RELEVANT LEGISLATION. 1-11 SECTION 2. COMMUNITY PROFILES I. INTRODUCTION.. 2-1 A. Location. 2-1 B. Topography/Geology . 2-2 C. Climate .. 2-2 II. GREENE COUNTY. 2-3 A. History.. 2-3 B. Demographic Summary .. 2-3 1. Population .. 2-3 2.DRAFT Housing . 2-4 3. Economy . 2-6 III. JONES COUNTY. 2-9 A. History.. 2-9 B. Demographic Summary .. 2-9 1. Population .. 2-9 2. Housing . 2-10 3. Economy . 2-12 IV. LENOIR COUNTY. 2-15 A. History.. 2-15 B. Demographic Summary .. 2-15 1. Population .. 2-15 2. Housing . 2-16 3. Economy . 2-18 V. PITT COUNTY. 2-21 A. History.. 2-21 B. Demographic Summary .. 2-21 1. Population .. 2-21 2. Housing . 2-22 DRAFT: FEBRUARY 13, 2015 PAGE i NEUSE RIVER BASIN REGIONAL HAZARD MITIGATION PLAN TABLE OF CONTENTS 3.
    [Show full text]
  • SD Front Cvr Color
    OCTOBER 1998 VOLUME 40 NUMBER 10 STORMSTORM DATADATA AND UNUSUAL WEATHER PHENOMENA WITH LATE REPORTS AND CORRECTIONS NATIONAL OCEANIC AND NATIONAL ENVIRONMENTAL SATELLITE NATIONAL CLIMATIC DATA CENTER noaa ATMOSPHERIC ADMINISTRATION DATA, AND INFORMATION SERVICE ASHEVILLE, N.C. Cover: The cement slab foundation is all that remains of this home in Seguin, near Lake Placid, TX. A flash flood near San Antonio, Texas killed 25 people and caused nearly $100 Million in property and crop damage. (Photograph courtesy of Larry Eblen, Warning Coordination Meteorologist, National Weather Service, San Antonio, Texas) TABLE OF CONTENTS Page Outstanding Storms of the Month ……………………………………………………………………………………….. 5 Storm Data and Unusual Weather Phenomena ………………………………………………………………………….. 7 Additions / Corrections ………………………………………………………………………………………………… 103 Reference Notes …………………………………………………………………………………………………………. 138 STORM DATA (ISSN 0039-1972) National Climatic Data Center Editor: Stephen Del Greco Assistant Editor: Stuart Hinson Editorial Staff: Noel Risnychok STORM DATA is prepared, funded, and distributed by the National Oceanic and Atmospheric Administration (NOAA). The Outstanding Storms of the Month section is prepared by the Data Operations Branch of the National Climatic Data Center. The Storm Data and Unusual Weather Phenomena narratives and Hurricane/Tropical Storm summaries are prepared by the National Weather Service. Monthly and annual statistics and summaries of tornado and lightning events resulting in deaths, injuries, and damage are compiled by cooperative efforts between the National Climatic Data Center and the Storm Prediction Center. STORM DATA contains all confirmed information on storms available to our staff at the time of publication. However, due to difficulties inherent in the collection of this type of data, it is not all-inclusive. Late reports and corrections are printed in each edition.
    [Show full text]
  • Virginia HURRICANES by Barbara Mcnaught Watson
    Virginia HURRICANES By Barbara McNaught Watson A hurricane is a large tropical complex of thunderstorms forming spiral bands around an intense low pressure center (the eye). Sustained winds must be at least 75 mph, but may reach over 200 mph in the strongest of these storms. The strong winds drive the ocean's surface, building waves 40 feet high on the open water. As the storm moves into shallower waters, the waves lessen, but water levels rise, bulging up on the storm's front right quadrant in what is called the "storm surge." This is the deadliest part of a hurricane. The storm surge and wind driven waves can devastate a coastline and bring ocean water miles inland. Inland, the hurricane's band of thunderstorms produce torrential rains and sometimes tornadoes. A foot or more of rain may fall in less than a day causing flash floods and mudslides. The rain eventually drains into the large rivers which may still be flooding for days after the storm has passed. The storm's driving winds can topple trees, utility poles, and damage buildings. Communication and electricity is lost for days and roads are impassable due to fallen trees and debris. A tropical storm has winds of 39 to 74 mph. It may or may not develop into a hurricane, or may be a hurricane in its dissipating stage. While a tropical storm does not produce a high storm surge, its thunderstorms can still pack a dangerous and deadly punch. Agnes was only a tropical storm when it dropped torrential rains that lead to devastating floods in Pennsylvania, Maryland, and Virginia.
    [Show full text]
  • FEMA Disaster Cost-Shares: Evolution and Analysis
    FEMA Disaster Cost-Shares: Evolution and Analysis Francis X. McCarthy Analyst in Emergency Management Policy March 9, 2010 Congressional Research Service 7-5700 www.crs.gov R41101 CRS Report for Congress Prepared for Members and Committees of Congress FEMA Disaster Cost-Shares: Evolution and Analysis Summary The Robert T. Stafford Disaster Relief and Emergency Assistance Act (The Stafford Act, P.L. 93- 288) contains discretion for the President to adjust cost-shares for the Public Assistance (PA) program, Sections 406 and 407 of the act, that provides assistance to states, local governments and non-profit organizations for debris removal and rebuilding of the public and non-profit infrastructure. The language of the Stafford Act defining cost-shares for the repair, restoration, and replacement of damaged facilities provides that the federal share “shall be not less than 75 percent.” These provisions have been in effect for over 20 years. While the authority to adjust the cost-share is long standing, the history of FEMA’s administrative adjustments and Congress’ legislative actions in this area, are of a more recent vintage. In all, there have been 222 cost-share adjustments of varying sizes and lengths of time. In 1998 FEMA promulgated, in regulation, a more consistent and open approach to cost-share adjustments. The overwhelming majority of these actions have been based on that regulatory authority and carried out by the executive branch through administrative actions. However, since 1997, and particularly in the wake of the difficult issues caused by the Gulf Coast storms of 2005, Congress has begun to exercise its authority to adjust cost-shares.
    [Show full text]
  • Characteristics of Tornadoes Associated with Land-Falling Gulf
    CHARACTERISTICS OF TORNADOES ASSOCIATED WITH LAND-FALLING GULF COAST TROPICAL CYCLONES by CORY L. RHODES DR. JASON SENKBEIL, COMMITTEE CHAIR DR. DAVID BROMMER DR. P. GRADY DIXON A THESIS Submitted in partial fulfillment of the requirements for the degree of Master of Science in the Department of Geography in the Graduate School of The University of Alabama TUSCALOOSA, ALABAMA 2012 Copyright Cory L. Rhodes 2012 ALL RIGHTS RESERVED ABSTRACT Tropical cyclone tornadoes are brief and often unpredictable events that can produce fatalities and create considerable economic loss. Given these uncertainties, it is important to understand the characteristics and factors that contribute to tornado formation within tropical cyclones. This thesis analyzes this hazardous phenomenon, examining the relationships among tropical cyclone intensity, size, and tornado output. Furthermore, the influences of synoptic and dynamic parameters on tornado output near the time of tornado formation were assessed among two phases of a tropical cyclone’s life cycle; those among hurricanes and tropical storms, termed tropical cyclone tornadoes (TCT), and those among tropical depressions and remnant lows, termed tropical low tornadoes (TLT). Results show that tornado output is affected by tropical cyclone intensity, and to a lesser extent size, with those classified as large in size and ‘major’ in intensity producing a greater amount of tornadoes. Increased values of storm relative helicity are dominant for the TCT environment while CAPE remains the driving force for TLT storms. ii ACKNOWLEDGMENTS I would like to thank my advisor and committee chair, Dr. Jason Senkbeil, and fellow committee members Dr. David Brommer and Dr. P. Grady Dixon for their encouragement, guidance and tremendous support throughout the entire thesis process.
    [Show full text]
  • Presentation
    7.A.1 TROPICAL CYCLONE TORNADOES – A RESEARCH AND FORECASTING OVERVIEW. PART 1: CLIMATOLOGIES, DISTRIBUTION AND FORECAST CONCEPTS Roger Edwards Storm Prediction Center, Norman, OK 1. INTRODUCTION those aspects of the remainder of the preliminary article Tropical cyclone (TC) tornadoes represent a relatively that was not included in this conference preprint, for small subset of total tornado reports, but garner space considerations. specialized attention in applied research and operational forecasting because of their distinctive origin within the envelope of either a landfalling or remnant TC. As with 2. CLIMATOLOGIES and DISTRIBUTION PATTERNS midlatitude weather systems, the predominant vehicle for tornadogenesis in TCs appears to be the supercell, a. Individual TCs and classifications particularly with regard to significant1 events. From a framework of ingredients-based forecasting of severe TC tornado climatologies are strongly influenced by the local storms (e.g., Doswell 1987, Johns and Doswell prolificacy of reports with several exceptional events 1992), supercells in TCs share with their midlatitude (Table 1). The general increase in TC tornado reports, relatives the fundamental environmental elements of noted as long ago as Hill et al. (1966), and in the sufficient moisture, instability, lift and vertical wind occurrence of “outbreaks” of 20 or more per TC (Curtis shear. Many of the same processes – including those 2004) probably is a TC-specific reflection of the recent involving baroclinicity at various scales – appear to major increase in overall tornado reports, particularly contribute to tornado production in both tropical and those of the weakest (F0/EF0) damage category in the midlatitude supercells. TCs do diverge somewhat from database.
    [Show full text]
  • U.S. Billion-Dollar Weather & Climate Disasters 1980-2021
    U.S. Billion-Dollar Weather & Climate Disasters 1980-2021 https://www.ncdc.noaa.gov/billions/ The U.S. has sustained 298 weather and climate disasters since 1980 in which overall damages/costs reached or exceeded $1 billion. Values in parentheses represent the 2021 Consumer Price Index cost adjusted value (if different than original value). The total cost of these 298 events exceeds $1.975 trillion. Drought Flooding Freeze Severe Storm Tropical Cyclone Wildfire Winter Storm 2021 Western Drought and Heatwave - June 2021: Western drought expands and intensifies across many western states. A historic heat wave developed for many days across the Pacific Northwest shattering numerous all-time high temperature records across the region. This prolonged heat dome was maximized over the states of Oregon and Washington and also extended well into Canada. These extreme temperatures impacted several major cities and millions of people. For example, Portland reached a high of 116 degrees F while Seattle reached 108 degrees F. The count for heat-related fatalities is still preliminary and will likely rise further. This combined drought and heat is rapidly drying out vegetation across the West, impacting agriculture and contributing to increased Western wildfire potential and severity. Total Estimated Costs: TBD; 138 Deaths Louisiana Flooding and Central Severe Weather - May 2021: Torrential rainfall from thunderstorms across coastal Texas and Louisiana caused widespread flooding and resulted in hundreds of water rescues. Baton Rouge and Lake Charles experienced flood damage to thousands of homes, vehicles and businesses, as more than 12 inches of rain fell. Lake Charles also continues to recover from the widespread damage caused by Hurricanes Laura and Delta less than 9 months before this flood event.
    [Show full text]
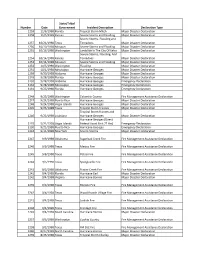
  • Identification of Disaster Code Declaration
    State/Tribal Number Date Government Incident Description Declaration Type 1259 11/6/1998 Florida Tropical Storm Mitch Major Disaster Declaration 1258 11/5/1998 Kansas Severe Storms and Flooding Major Disaster Declaration Severe Storms, Flooding and 1257 10/21/1998 Texas Tornadoes Major Disaster Declaration 1256 10/19/1998 Missouri Severe Storms and Flooding Major Disaster Declaration 1255 10/16/1998 Washington Landslide In The City Of Kelso Major Disaster Declaration Severe Storms, Flooding, And 1254 10/14/1998 Kansas Tornadoes Major Disaster Declaration 1253 10/14/1998 Missouri Severe Storms and Flooding Major Disaster Declaration 1252 10/5/1998 Washington Flooding Major Disaster Declaration 1251 10/1/1998 Mississippi Hurricane Georges Major Disaster Declaration 1250 9/30/1998 Alabama Hurricane Georges Major Disaster Declaration 1249 9/28/1998 Florida Hurricane Georges Major Disaster Declaration 3133 9/28/1998 Alabama Hurricane Georges Emergency Declaration 3132 9/28/1998 Mississippi Hurricane Georges Emergency Declaration 3131 9/25/1998 Florida Hurricane Georges Emergency Declaration 2248 9/25/1998 Washington Columbia County Fire Management Assistance Declaration 1247 9/24/1998 Puerto Rico Hurricane Georges Major Disaster Declaration 1248 9/24/1998 Virgin Islands Hurricane Georges Major Disaster Declaration 1245 9/23/1998 Texas Tropical Storm Frances Major Disaster Declaration Tropical Storm Frances and 1246 9/23/1998 Louisiana Hurricane Georges Major Disaster Declaration Hurricane Georges (Direct 3129 9/21/1998 Virgin Islands Federal
    [Show full text]