DOCSLIB.ORG

Physicochemical Properties of Drugs in Solution

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Physicochemical Properties of Drugs in Solution 09_1439PP_CH03 17/10/05 10:47 pm Page 55 3 Physicochemical properties of drugs in solution 3.1 Concentration units 56 3.5 Ionisation of drugs in solution 75 3.2 Thermodynamics – a brief 3.6 Diffusion of drugs in solution 89 introduction 57 Summary 90 3.3 Activity and chemical potential 62 References 91 3.4 Osmotic properties of drug solutions 69 In this chapter we examine some of the important physicochemical properties of drugs in aqueous solution which are of relevance to such liquid dosage forms as injections, solutions, and eye drops. Some basic thermodynamic concepts will be introduced, particularly that of thermo- dynamic activity, an important parameter in determining drug potency. It is important that parenteral solutions are formulated with osmotic pressure similar to that of blood serum; in this chapter we will see how to adjust the tonicity of the formulation to achieve this aim. Most drugs are at least partially ionised at physiological pH and many studies have suggested that the charged group is essential for biological activity. We look at the influence of pH on the ionisation of several types of drug in solution and consider equations that allow the calculation of the pH of solutions of these drugs. First, however, we recount the various ways to express the strength of a solution, since it is of fundamental importance that we are able to interpret the various units used to denote solution concentration and to understand their interrelationships, not least in practice situations. Physicochemical Principles of Pharmacy, 4th edition (ISBN: 0 85369 608 X) © Pharmaceutical Press 2006 09_1439PP_CH03 17/10/05 10:47 pm Page 56 3.1 Concentration units is an accepted SI unit. Molarity may be con- verted to SI units using the relationship 1 mol litre 01 # 1 mol dm 03 # 10 3 mol m 03. A wide range of units is commonly used to Interconversion between molarity and molal- express solution concentration, and confusion ity requires a knowledge of the density of the often arises in the interconversion of one solution. set of units to another. Wherever possible Of the two units, molality is preferable for a throughout this book we have used the SI precise expression of concentration because it system of units. Although this is the currently does not depend on the solution temperature recommended system of units in Great as does molarity; also, the molality of a com- Britain, other more traditional systems are still ponent in a solution remains unaltered by the widely used and these will be also described in addition of a second solute, whereas the this section. molarity of this component decreases because the total volume of solution increases follow- ing the addition of the second solute. 3.1.1 Weight concentration Concentration is often expressed as a weight of solute in a unit volume of solution; for 3.1.3 Milliequivalents example, g dm03, or % wv, which is the number of grams of solute in 100 cm3 of solu- The unit milliequivalent (mEq) is commonly tion. This is not an exact method when used clinically in expressing the concentration working at a range of temperatures, since of an ion in solution. The term ‘equivalent’, or the volume of the solution is temperature- gram equivalent weight, is analogous to the dependent and hence the weight concentra- mole or gram molecular weight. When tion also changes with temperature. monovalent ions are considered, these two Whenever a hydrated compound is used, terms are identical. A 1 molar solution of it is important to use the correct state of sodium bicarbonate, NaHCO3, contains 1 mol ! − or 1 Eq of Na and 1 mol or 1 Eq of HCO3 per hydration in the calculation of weight litre (dm03) of solution. With multivalent concentration. Thus 10% w v CaCl2 (anhy- drous) is approximately equivalent to 20% wv ions, attention must be paid to the valency of CaCl ·6H O and consequently the use of the each ion; for example, 10% w v CaCl2·2H2 O 2 2 2! vague statement ‘10% calcium chloride’ could contains 6.8 mmol or 13.6 mEq of Ca in 3 result in gross error. The SI unit of weight 10 cm . 1 concentration is kg m03 which is numerically The Pharmaceutical Codex gives a table of equal to g dm03. milliequivalents for various ions and also a simple formula for the calculation of milli- equivalents per litre (see Box 3.1). 3.1.2 Molarity and molality In analytical chemistry a solution which contains 1 Eq dm03 is referred to as a normal These two similar-sounding terms must not be solution. Unfortunately the term ‘normal’ is confused. The molarity of a solution is the also used to mean physiologically normal with number of moles (gram molecular weights) of reference to saline solution. In this usage, a solute in 1 litre (1 dm3) of solution. The molal- physiologically normal saline solution con- ity is the number of moles of solute in 1 kg of tains 0.9 g NaCl in 100 cm3 aqueous solution solvent. Molality has the unit, mol kg01, which and not 1 equivalent (58.44 g) per litre. Physicochemical Principles of Pharmacy, 4th edition (ISBN: 0 85369 608 X) © Pharmaceutical Press 2006 09_1439PP_CH03 17/10/05 10:47 pm Page 57 Thermodynamics – a brief introduction 57 (b) 9 g of sodium chloride are dissolved in Box 3.1 Calculation of milliequivalents 991 g of water (assuming density # 1gdm03). The number of milliequivalents in 1 g of substance is Therefore 1000 g of water contains 9.08 g of given by sodium chloride # 0.155 moles, i.e. molality # valency x 1000 x no. of specified 0.155 mol kg01. units in 1 atom/molecule/ion mEq = (c) Mole fraction of sodium chloride, x , is atomic, molecular or ionic weight 1 given by For example, CaCl2·2H2 O (mol. wt. # 147.0) n1 0.154 − 2 × 1000 × 1 x = = = × 3 2+ = 1 2.79 10 mEq Ca in 1 g CaCl2 · 2H2 O n + n 0.154 + 55.06 147.0 1 2 = 13.6 mEq (Note 991 g of water contains 99118 and moles, i.e. n2 # 55.06.) ! × × (d) Since Na is monovalent, the number of − 1 1000 2 ! mEq Cl in 1 g CaCl · 2H O = milliequivalents of Na # number of milli- 2 2 147.0 moles. = 13.6 mEq 03 that is, each gram of CaCl ·2H O represents 13.6 mEq Therefore the solution contains 154 mEq dm 2 2 ! of calcium and 13.6 mEq of chloride of Na . 3.1.4 Mole fraction 3.2 Thermodynamics – a brief introduction The mole fraction of a component of a solu- tion is the number of moles of that com- The importance of thermodynamics in the ponent divided by the total number of moles pharmaceutical sciences is apparent when it is present in solution. In a two-component realised that such processes as the partitioning (binary) solution, the mole fraction of solvent, of solutes between immiscible solvents, the # ! x1, is given by x1 n1 (n1 n2), where n1 and solubility of drugs, micellisation and drug– n2 are respectively the numbers of moles of receptor interaction can all be treated in solvent and of solute present in solution. thermodynamic terms. This brief section Similarly, the mole fraction of solute, x2, is merely introduces some of the concepts of # ! given by x2 n2 (n1 n2). The sum of the thermodynamics which are referred to through- mole fractions of all components is, of course, out the book. Readers requiring a greater ! # unity, i.e. for a binary solution, x1 x2 1. depth of treatment should consult standard texts on this subject.2, 3 EXAMPLE 3.1 Units of concentration Isotonic saline contains 0.9% wv of sodium 3.2.1 Energy chloride (mol. wt. # 58.5). Express the concen- tration of this solution as: (a) molarity; (b) Energy is a fundamental property of a system. molality; (c) mole fraction and (d) milliequiv- Some idea of its importance may be gained by alents of Na! per litre. Assume that the density considering its role in chemical reactions, of isotonic saline is 1 g cm03. where it determines what reactions may occur, how fast the reaction may proceed and in Answer which direction the reaction will occur. (a) 0.9% wv solution of sodium chloride Energy takes several forms: kinetic energy is contains 9 g dm03 # 0.154 mol dm03. that which a body possesses as a result of its Physicochemical Principles of Pharmacy, 4th edition (ISBN: 0 85369 608 X) © Pharmaceutical Press 2006 09_1439PP_CH03 17/10/05 10:47 pm Page 58 58 Chapter 3 • Physicochemical properties of drugs in solution motion; potential energy is the energy which changes in heat energy, which were not a body has due to its position, whether gravi- encompassed in the conservation law. tational potential energy or coulombic poten- It follows from equation (3.2) that a system tial energy which is associated with charged which is completely isolated from its sur- particles at a given distance apart. All forms of roundings, such that it cannot exchange heat energy are related, but in converting between or interact mechanically to do work, cannot the various types it is not possible to create or experience any change in its internal energy. destroy energy. This forms the basis of the law In other words the internal energy of an isolated of conservation of energy. system is constant – this is the first law of The internal energy U of a system is the sum thermodynamics. of all the kinetic and potential energy contri- butions to the energy of all the atoms, ions and molecules in that system.
Load more

Recommended publications
  • Drug-Induced Angle-Closure Glaucoma
    10.5005/jp-journals-10008-1100 ArujREVIEW K Khurana ARTICLE et al Drug-induced Angle-Closure Glaucoma Aruj K Khurana, Bhawna Khurana, Ashok K Khurana Regional Institute of Ophthalmology, Post Graduate Institute of Medical Sciences, Rohtak, Haryana, India Correspondence: Ashok K Khurana, Senior Professor, Regional Institute of Ophthalmology, Post Graduate Institute of Medical Sciences, Rohtak, Haryana, India ABSTRACT Drug-induced angle-closure glaucoma is an important entity for the ophthalmologist as well as the general physician as it represents a preventable cause of potential blindness. This brief review highlights the fact that a high index of suspicion, in a susceptible individual followed by confirmation on appropriate imaging modality (UBM, ultrasound or anterior segment OCT) can alleviate the threat to sight and also help to institute appropriate therapy. Keywords: Acute angle closure, Drug-induced glaucoma. INTRODUCTION factors exist for this syndrome.9 Other sulfa-based drugs known Drug-induced angle-closure glaucoma is an important entity to be associated with AACG: Acetazolamide, hydrochloro- 10 for the ophthalmologist as well as the general physician as it thiazide and cotrimoxazole. represents a preventable cause of potential blindness.1 Acute Anticholinergic drugs implicated in the causation of AACG angle-closure glaucoma can develop in a susceptible individual include atropine, homatropine, cyclopentolate and ipratropium by various classes of drugs.2 Practitioners using any of these bromide.10,11 Atropine is often used to treat bradycardia, drugs should be aware of their potential to cause acute angle especially related to general anesthesia. Postoperative AACG closure, such that a patient presenting with signs or symptoms has been reported in patients after general anesthesia for of acute angle closure should be immediately referred to an abdominal, orthopedic, facial and endoscopic surgery.12 3 ophthalmologist.
    [Show full text]
  • Appendix A: Potentially Inappropriate Prescriptions (Pips) for Older People (Modified from ‘STOPP/START 2’ O’Mahony Et Al 2014)
    Appendix A: Potentially Inappropriate Prescriptions (PIPs) for older people (modified from ‘STOPP/START 2’ O’Mahony et al 2014) Consider holding (or deprescribing - consult with patient): 1. Any drug prescribed without an evidence-based clinical indication 2. Any drug prescribed beyond the recommended duration, where well-defined 3. Any duplicate drug class (optimise monotherapy) Avoid hazardous combinations e.g.: 1. The Triple Whammy: NSAID + ACE/ARB + diuretic in all ≥ 65 year olds (NHS Scotland 2015) 2. Sick Day Rules drugs: Metformin or ACEi/ARB or a diuretic or NSAID in ≥ 65 year olds presenting with dehydration and/or acute kidney injury (AKI) (NHS Scotland 2015) 3. Anticholinergic Burden (ACB): Any additional medicine with anticholinergic properties when already on an Anticholinergic/antimuscarinic (listed overleaf) in > 65 year olds (risk of falls, increased anticholinergic toxicity: confusion, agitation, acute glaucoma, urinary retention, constipation). The following are known to contribute to the ACB: Amantadine Antidepressants, tricyclic: Amitriptyline, Clomipramine, Dosulepin, Doxepin, Imipramine, Nortriptyline, Trimipramine and SSRIs: Fluoxetine, Paroxetine Antihistamines, first generation (sedating): Clemastine, Chlorphenamine, Cyproheptadine, Diphenhydramine/-hydrinate, Hydroxyzine, Promethazine; also Cetirizine, Loratidine Antipsychotics: especially Clozapine, Fluphenazine, Haloperidol, Olanzepine, and phenothiazines e.g. Prochlorperazine, Trifluoperazine Baclofen Carbamazepine Disopyramide Loperamide Oxcarbazepine Pethidine
    [Show full text]
  • Chlorphenamine Maleate)
    Package leaflet: Information for the patient Chlorphenamine 10 mg/ml Solution for Injection (Chlorphenamine Maleate) Read all of this leaflet carefully before you start taking this medicine because it contains important information for you. − Keep this leaflet. You may need to read it again. − If you have any further questions, ask your doctor or nurse. − If you get any side effects, talk to your doctor or nurse. This includes any possible side effects not listed in this leaflet. See section 4. What is in this leaflet: 1. What Chlorphenamine is and what it is used for 2. What you need to know before Chlorphenamine is given 3. How Chlorphenamine is given 4. Possible side effects 5. How to store Chlorphenamine 6. Contents of the pack and other information 1. What Chlorphenamine is and what it is used for Chlorphenamine 10 mg/ml Solution for Injection contains the active ingredient chlorphenamine maleate which is an antihistamine. Chlorphenamine is indicated in adults and children (aged 1 month to 18 years) for the treatment of acute allergic reactions. These medicines inhibit the release of histamine into the body that occurs during an allergic reaction. This product relieves some of the main symptoms of a severe allergic reaction. 2. What you need to know before Chlorphenamine is given You MUST NOT be given Chlorphenamine: if you are allergic to chlorphenamine maleate or any of the other ingredients of this medicine (listed in section 6) if you have had monoamine oxidase inhibitor (MAOI) antidepressive treatment within the past 14 days. Warnings and precautions Talk to your doctor or nurse before you are given this medicine if you: are being treated for an overactive thyroid or enlarged prostate gland have epilepsy, raised blood pressure within the eye or glaucoma, very high blood pressure, heart, liver, asthma or other chest diseases.
    [Show full text]
  • Prescribing Trends of Antihistamines in the Outpatient Setting in Al-Kharj
    Prescribing Trends of Antihistamines in the Outpatient Setting in Al-Kharj Nehad J. Ahmed1*, Menshawy A. Menshawy2 1Department of Clinical Pharmacy, College of Pharmacy, Prince Sattam Bin Abdulaziz University, Al-Kharj, Saudi Arabia, 2Department of Medicinal chemistry, College of Pharmacy, Prince Sattam Bin Abdulaziz University, Al-Kharj, Saudi Arabia Abstract Aim: This study aims to illustrate the prescribing trends of antihistamines in the outpatient setting in Al-Kharj. Materials and Methods: This is a retrospective study that included the evaluation of antihistamines in the outpatient setting in a public hospital in Al-Kharj. The data were collected from the pharmacy-based computer system. Results: The total number of prescriptions that included antihistamines was 799. Most of the prescribed ORIGINAL ARTICLE ARTICLE ORIGINAL antihistamines were first-generation sedating antihistamines (chlorphenamine and diphenhydramine) (66.33%). About 63.20% of the prescribed antihistamines included chlorpheniramine followed by cetirizine (19.27%) and loratadine (14.39%). Conclusion: Antihistamines were prescribed commonly in the outpatient setting mainly first-generation sedating antihistamines. It is recommended to increase the awareness of health- care providers about the efficacy and the side effects of antihistamines and to encourage them to use these agents wisely. Key words: Antihistamines, outpatient, prescribing, trends INTRODUCTION In addition, antihistamines have been classified as sedating antihistamines (first-generation antihistamines) and non- ntihistamines are used in the sedating antihistamines (second-generation antihistamines).[4] management of allergic conditions. Sedating antihistamines include chlorphenamine, clemastine, They are useful for treating the itching hydroxyzine, alimemazine, cyproheptadine, promethazine, A [1] and ketotifen.[4] Non-sedating antihistamines include that results from the release of histamine.
    [Show full text]
  • Non-Steroidal Drug-Induced Glaucoma MR Razeghinejad Et Al 972
    Eye (2011) 25, 971–980 & 2011 Macmillan Publishers Limited All rights reserved 0950-222X/11 www.nature.com/eye 1,2 1 1 Non-steroidal drug- MR Razeghinejad , MJ Pro and LJ Katz REVIEW induced glaucoma Abstract vision. The majority of drugs listed as contraindicated in glaucoma are concerned with Numerous systemically used drugs are CAG. These medications may incite an attack in involved in drug-induced glaucoma. Most those individuals with narrow iridocorneal reported cases of non-steroidal drug-induced angle.3 At least one-third of acute closed-angle glaucoma are closed-angle glaucoma (CAG). glaucoma (ACAG) cases are related to an Indeed, many routinely used drugs that have over-the-counter or prescription drug.1 Prevalence sympathomimetic or parasympatholytic of narrow angles in whites from the Framingham properties can cause pupillary block CAG in study was 3.8%. Narrow angles are more individuals with narrow iridocorneal angle. The resulting acute glaucoma occurs much common in the Asian population. A study of a more commonly unilaterally and only rarely Vietnamese population estimated a prevalence 4 bilaterally. CAG secondary to sulfa drugs is a of occludable angles at 8.5%. The reported bilateral non-pupillary block type and is due prevalence of elevated IOP months to years to forward movement of iris–lens diaphragm, after controlling ACAG with laser iridotomy 5,6 which occurs in individuals with narrow or ranges from 24 to 72%. Additionally, a open iridocorneal angle. A few agents, significant decrease in retinal nerve fiber layer including antineoplastics, may induce thickness and an increase in the cup/disc ratio open-angle glaucoma.
    [Show full text]
  • Studies in Laboratory Animals to Assess the Safety of Anti-Inflammatory Agents in Acute Porphyria
    Ann Rheum Dis: first published as 10.1136/ard.46.7.540 on 1 July 1987. Downloaded from Annals of the Rheumatic Diseases, 1987; 46, 540-542 Studies in laboratory animals to assess the safety of anti-inflammatory agents in acute porphyria KENNETH E L McCOLL, GEORGE G THOMPSON, AND MICHAEL R MOORE From the University Department of Medicine, Western Infirmary, Glasgow SUMMARY The safety of various anti-inflammatory drugs in acute porphyria was assessed by examining their effect on rat hepatic haem synthesis. Azapropazone, chloroquine, and gold increased 6-aminolaevulinic acid (ALA) synthase activity, indicating that they are liable to precipitate porphyric crises. Aspirin, ibuprofen, indomethacin, ketoprofen, flurbiprofen, phenylbutazone, naproxen, prednisolone, and penicillamine did not increase ALA synthase activity and should be safe in porphyria. Though these animal studies can be used as a guide to prescribing in patients with acute porphyria, some caution is still required as species may vary in their response to inducing agents. Key words: chloroquine, azapropazone, gold, b-aminolaevulinic acid synthase. copyright. The acute hepatic porphyrias which comprise acute controlling enzyme of haem biosynthesis 6- intermittent porphyria, hereditary coproporphyria, aminolaevulinic acid (ALA) synthase in rat hepatic and variegate porphyria are examples of pharma- tissue. To confirm the reliability of the animal cogenetic disease. They are the result of deficien- model, phenobarbitone was also tested. For each cies of individual enzymes in the pathway of haem drug examined six male Sprague-Dawley rats re- biosynthesis and are inherited in an autosomal ceived the test drug and six control rats received the dominant fashion.2 Subjects with the genetic trait appropriate placebo solution.
    [Show full text]
  • Drug-Induced Peptic Ulcer Disease
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by OAR@UM risk populations only.7 The prevalence of endoscopically confirmed gastrointestinal ulcers in NSAID users is quoted to be between 15% and 30%. Between 12% to 30% of NSAID-induced ulcers are gastric ulcers, whereas 2% to 19% are duodenal ulcers. NSAID-induced ulcers are symptomatic only in 1% of patients after three to six months and in 2 to 4% of patients after one year. Inappropriately they do not correlate well with pain because the analgesic action of NSAIDs may mask the ulcer pain.2 Drug-induced peptic Understanding the method by which NSAIDs cause gastric damage has helped in the development of prophylactic agents that ulcer disease 1 red uce their toxicity. The mechanism by which NSAIDs are thought to damage the Valerie Vella B Pharm(Hons), PgDip Clin Pharm (Aberdeen) gastrointestinal tract is four-fold. Clinical Pharmacist, St Luke’s Hospital, Guardamangia, Malta a) Topical injury Email: [email protected] Originally it was thought that NSAIDs damaged the gastric epithelium by Key words: Peptic ulcer, medicines, prostaglandins, gastrointestinal protection, intracellular accumulation of these drugs in gastrointestinal toxicity an ionised state.1 However the fact that enteric-coated formulations, pro-drugs, For more than a century, peptic ulcer disease has been a rectal and parenteral administration of 1 major cause of morbidity and mortality. Peptic ulcer disease NSAIDs still resulted in gastrointestinal is a heterogeneous group of disorders involving the damage despite the apparent absence of gastrointestinal tract and results from an imbalance between direct mucosal contact implies a minor role the aggressive forces of gastric acid and pepsin and the for topical injury1,2.
    [Show full text]
  • Your Child's Emergency Allergy Pack with Antihistamine
    Your Child’s Emergency Allergy Pack with Antihistamine Patient information Paediatric Department Watford General Hospital Hemel Hempstead Hospital If you need this leaflet in another language, large print, Braille or audio version, please call 01923 217 187 or email [email protected] Author Dr Ashley Reece Department Paediatrics Ratified Date / Review Date Feb 2021 / Feb 2024 Version Number / ID Number 40-1104-V1 Why does my child I need an Allergy Action Pack? An allergy action pan is a kit contianing evrything you need in case of an allergic reaction. Is my/ my child’s allergy severe? There is no such thing as a mild or severe allergy as reactions are always unpredicatble. However we do classify reactions as mild, moderate or severe. While it follows that a severe reaction makes the anxiety about the severity of the next reaction high, we cannot predict the severity of subsequent reactions. However there are some foods and some allergies which are assessed as having very low risk of a significant reaction. The way to manage your child with their allergy is to ensure you have the best possible safety net in case of an unforeseen reaction. Your doctor will give you a specific allergy plan (like the one to the right) which you should also give to your child’s school. Generally allergy is mananged by: You MUST avoid any foods which you know your child is allergic to. Avoidance Take care with labels and risk assess any new foods and when eating out in a restaurant or from a take-away.
    [Show full text]
  • Title 16. Crimes and Offenses Chapter 13. Controlled Substances Article 1
    TITLE 16. CRIMES AND OFFENSES CHAPTER 13. CONTROLLED SUBSTANCES ARTICLE 1. GENERAL PROVISIONS § 16-13-1. Drug related objects (a) As used in this Code section, the term: (1) "Controlled substance" shall have the same meaning as defined in Article 2 of this chapter, relating to controlled substances. For the purposes of this Code section, the term "controlled substance" shall include marijuana as defined by paragraph (16) of Code Section 16-13-21. (2) "Dangerous drug" shall have the same meaning as defined in Article 3 of this chapter, relating to dangerous drugs. (3) "Drug related object" means any machine, instrument, tool, equipment, contrivance, or device which an average person would reasonably conclude is intended to be used for one or more of the following purposes: (A) To introduce into the human body any dangerous drug or controlled substance under circumstances in violation of the laws of this state; (B) To enhance the effect on the human body of any dangerous drug or controlled substance under circumstances in violation of the laws of this state; (C) To conceal any quantity of any dangerous drug or controlled substance under circumstances in violation of the laws of this state; or (D) To test the strength, effectiveness, or purity of any dangerous drug or controlled substance under circumstances in violation of the laws of this state. (4) "Knowingly" means having general knowledge that a machine, instrument, tool, item of equipment, contrivance, or device is a drug related object or having reasonable grounds to believe that any such object is or may, to an average person, appear to be a drug related object.
    [Show full text]
  • Anticholinergic Drugs and Dementia
    DEMENTIA Q&A 24 Anticholinergic drugs and dementia Anticholinergics are a class of drug used to treat a wide variety of medical conditions. As with any medication, anticholinergics can have many beneficial effects, but these need to be balanced against a number of potential risks. This sheet provides information about how these drugs work as well as the impact that they may have in respect to dementia risk and cognitive functioning. What are anticholinergics? in time.4 It has been estimated that in Australia, 33% of people over the age of 65 years take enough Anticholinergics are generally used to inhibit the medications with anticholinergic effects to potentially involuntary movements of muscles or balance the increase their risk of harm.5 The use of anticholinergics production of various chemicals within the body. They is more common in older people because these drugs have been used in treating a wide variety of medical are prescribed for the symptomatic management of conditions including symptoms of psychosis (which medical conditions that often occur in later life. can be caused by bipolar disorder and schizophrenia), depression, urinary incontinence (e.g. overactive How do anticholinergic drugs work? bladder), gastrointestinal spasms, allergies, respiratory Anticholinergics are a class of drug that block the conditions (such as asthma and chronic obstructive action of acetylcholine in the nervous system, a pulmonary disease), Parkinson’s disease, conditions chemical (neurotransmitter) that is used to control concerning muscles in the eye and pupil dilation, messages travelling from one cell to another. They do nausea, sleep disorders and cardiovascular complaints this by blocking the binding of acetylcholine to its (slow heart rhythms) (Table 1).1,2 Some cold and flu receptor in the nerve cells.
    [Show full text]
  • Pharmacology of Ophthalmic Agents
    Ophthalmic Pharmacology Richard Alan Lewis M.D., M.S., PHARMACOLOGY FOPS PHARMACOKINETICS OF Professor, Departments of Ophthalmology, • The study of the absorption, OPHTHALMIC Medicine, Pediatrics, and Molecular distribution, metabolism, AGENTS and Human Genetics and excretion of a drug or and the National School of Tropical agent Introduction and Review Medicine Houston, Texas PHARMACOKINETICS Factors Affecting Drug Penetration Factors Affecting Drug Penetration into Ocular Tissues • A drug can be delivered to ocular tissue: into Ocular Tissues – Locally: • Drug concentration and solubility: The higher the concentration the better the penetration, • Surfactants: The preservatives in ocular • Eye drop but limited by reflex tearing. preparations alter cell membrane in the cornea • Ointment and increase drug permeability, e.g., • Viscosity: Addition of methylcellulose and benzalkonium and thiomersal • Periocular injection polyvinyl alcohol increases drug penetration by • pH: The normal tear pH is 7.4; if the drug pH is • Intraocular injection increasing the contact time with the cornea and altering corneal epithelium. much different, it will cause reflex tearing. – Systemically: • Lipid solubility: Because of the lipid rich • Drug tonicity: When an alkaloid drug is put in • Orally environment of the epithelial cell membranes, relatively alkaloid medium, the proportion of the uncharged form will increase, thus more • IM the higher lipid solubility, the more the penetration. • IV penetration. FLUORESCEIN FLUORESCEIN Chemistry Dosage ● C20H1205, brown crystal ● Adults: 500-750 mg IV ● M.W. 322.3 e.g., 3 cc 25% solution ● Peak absorption 485-500 nm. 5 cc 10% solution ● Peak emission 520-530 nm. ● Children: 1.5-2.5 mg/kg IV Richard Alan Lewis, M.D., M.S.
    [Show full text]
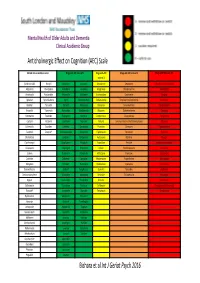
  • AEC Traffic Light System
    Mental Health of Older Adults and Dementia Clinical Academic Group Anticholinergic Effect on Cognition (AEC) Scale Limited data so unable to score Drugs with AEC score of 0 Drugs with AEC Drugs with AEC score of 2 Drugs with AEC score of 3 score of 1 Alendronic Acid Ramipril Alprazolam Lovastatin Amiodarone Amantadine Alimemazine (trimeprazine) Allopurinol Rivaroxaban Amlodipine Lurasidone Aripiprazole Chlorphenamine Amitriptyline Anastrozole Rosuvastatin Amoxycillin Meloxicam Bromocriptine Desipramine Atropine Apixaban Spironolactone Aspirin Metoclopramide Carbamazepine Dicycloverine (dicyclomine) Benztropine Baclofen Tamoxifen Atenolol Metoprolol Citalopram Dimenhydrinate Chlorpromazine Bisoprolol Topiramate Atorvastatin Moclobemide Diazepam Diphenhydramine Clemastine Bumetanide Tizanidine Buproprion Morphine Domperidone Disopyramide Clomipramine Captopril Verapamil Cepahlexin Naproxen Fentanyl Levomepromazine (methotrimeprazine) Clozapine Carbimazole Zopiclone Cetirizine Omeprazole Fluoxetine Olanzapine Cyproheptadine Carvedilol Zotepine* Chlordiazepoxide Paracetamol Fluphenazine Paroxetine Dothiepin Chlortalidone Cimetidine Pantoprazole Hydroxyzine Pethidine Doxepin Clarithromycin Ciprofloxacin Pravastatin Iloperidone Pimozide Hyoscine hydrobromide Clonazepam Clopidogrel Propranolol Lithium Prochlorperazine Imipramine Codeine Darifenacin Rabeprazole Mirtazapine Promazine Lofepramine Colchicine Diclofenac Ranitidine Perphenazine Propantheline Nortriptyline Dabigatran Diltiazem Risperidone Prednisolone Quetiapine Orphenadrine Dexamethasone
    [Show full text]