DOCSLIB.ORG

99 UPWELLING in the GULF of GUINEA Results of a Mathematical

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
99 UPWELLING in the GULF of GUINEA Results of a Mathematical 99 UPWELLING IN THE GULF OF GUINEA Results of a mathematical model 2 2 6 5 0 A. BAH Mécanique des Fluides géophysiques, Université de Liège, Liège (Belgium) ABSTRACT A numerical simulation of the oceanic response of an x-y-t two-layer model on the 3-plane to an increase of the wind stress is discussed in the case of the tro­ pical Atlantic Ocean. It is shown first that the method of mass transport is more suitable for the present study than the method of mean velocity, especially in the case of non-linearity. The results indicate that upwelling in the oceanic equatorial region is due to the eastward propagating equatorially trapped Kelvin wave, and that in the coastal region upwelling is due to the westward propagating reflected Rossby waves and to the poleward propagating Kelvin wave. The amplification due to non- linearity can be about 25 % in a month. The role of the non-rectilinear coast is clearly shown by the coastal upwelling which is more intense east than west of the three main capes of the Gulf of Guinea; furthermore, by day 90 after the wind's onset, the maximum of upwelling is located east of Cape Three Points, in good agree­ ment with observations. INTRODUCTION When they cross over the Gulf of Guinea, monsoonal winds take up humidity and subsequently discharge it over the African Continent in the form of precipitation (Fig. 1). The upwelling observed during the northern hemisphere summer along the coast of the Gulf of Guinea can reduce oceanic evaporation, and thereby affect the rainfall pattern in the SAHEL region. Years of intense upwelling could be very dry and years of reduced upwelling should result in periods of relatively high rainfall. Clearly, a better understanding of the upwelling regime might contribute significantly to improved land-use. Many investigators have attempted to explain the generation and evolution of up­ welling in the Gulf of Guinea. It was soon apparent that localJwinds could not provide an adequate forcing mechanism (Houghton, 1976). Philander (197$) concluded that the 100 Fig. 1. Sketch of the monsoon wind pattern over the Gulf of Guinea (after Dhonneur, 1974). upwelling is not due to local oceanic circulation, but rather is part of the large scale oceanic circulation system. This explanation seems reasonable since Adamec and O'Brien (1978) have already shown that variation of the trade winds regime in the western tropical Atlantic Ocean could excite an equatorially trapped Kelvin wave which would induce upwelling on its way eastwards (see also Moore, 1968; Moore and Philander, 1977; Moore et al., 1978). But their study does not explain the irregular intensification of upwelling locally along the northern coast of the Gulf of Guinea. Some previous workers have tried to demonstrate the effects of zonal and meridio­ nal coasts on equatorial waves (Philander, 1979; Weisberg et al., 1979). Recently, the study of Clarke (1979) dealt with local longshore variations in the wind stress and the resulting long trapped waves travelling along the northern coast of the Gulf of Guinea. Yoshida (1967) and Arthur (1965) have described enhanced upwelling near a cape. Their results suggest that the role played by the irregular geometry of the northern coast of the Gulf of Guinea should be examined. This is the object of the present paper. r 101 1. THE NUMERICAL MODEL 1.1. Model geometry In contrast with the model developed by Adamec and O'Brien (1978), our model deals with a non-rectilinear coastline. The numerical simulation concerns the oceanic res­ ponse of an x-y-t two-layer model on the 3-plane to an increase in the wind stress X and y increase eastwards and northwards, respectively. The bottom of the Ocean is assumed flat, and the depth of the upper layer is constant. Fig. 2 shows the geometry of the basin, where horizontal dimensions Lx and L are respectively 3000 and 5000 km . 1000 km Fig. 2. The model geometry with the irregular coastline. 1.2. Model formulation The quasi-hydrostatic and Boussinesq approximations are made. The layer densities Pi and p2 are constant. The effects of atmospheric pressure, tides and thermohaline mixing are neglected. If there is no pressure gradient in the second layer (i.e. Vp2 = 0), the linea­ rized equations for a two-layer viscous flow reduce to : 5u (1) at PH0 gyu - g ^ (2) at 102 &♦«<&* g" ° The equations governing the mass transport are, on the other hand, = ßyV - g'H + — + A V2U (4) 3t 3x p f - (5) f * s * § - » where A and A h are the horizontal eddy viscosities (assumed constant), Ho the undisturbed depth of the upper layer, h the perturbation of the upper layer thick­ ness, H the total (disturbed) depth and P 2 “ Pi g ' _ g ---------------- P 2 the reduced gravity. Definitions of the other terms are obvious. This model repre­ sents the simplest formulation of the first baroclinie response. In non-dimensional form, the system of equations (1-3) can be rewritten (Bah, 1979; Bah et al., 1979) : 9u 9h T 92u 92u — = yv - a! — + a2 — + a 3 — - + ai+ - . (7) 9t 9x p 3X2 9y 9v 9h t 92v 92v ^ = - yu - ^ + a2 - + a3 + a, ^ (8) |h + ai |¡L + |v = 0 {9) at 9x 9y where ai = ; a2 = ß-^g'-374 hÔ 7/4 ; a , = A 4 B1 g'■ H.' 3/4 ; a, = Aß* (g ' H0 )' 3/4 X Ly /g'Ho ßLx Lx and L y are the zonal and the meridional length scales respectively. Working with the system of equations (4-6) one gets from the equation of conti­ nuity 9h 9u , 9v 9u 9h , 9v 9h . im — + a] — + — + aih — + a lU — + h -5- + v — = 0 (10) 9t 9x 9y 9x 9x 9y 9y 103 Thus, working with equations (1-3) relative to the mean velocity results in ne­ glecting the last four terms of equation (10), which is equivalent to neglecting contributions at least of the same order of magnitude as the respective second terms of the right side of eqs (7) and (8). The values for , a 2 , a 3 and a^ for the case of a 50 m depth are respec­ tively 2.24 , 4.47 X 1CT 2.24 X 10 3 and 4.47 x 10"* (Bah, 1979). 1.3. Numerical scheme The numerical model uses the numerical scheme developed by Ronday (1976) u and V are computed according to the following spatial grid. I I I I I I I I 2 1+2 9-- -©- 0 - for I i i for I i i for I i I i 2 I i ' “ t □ - - - AY I i 2 1 - 2 0 ----- — © - i ! I 2 J 2 J 2 J + 2 ■ AX Fig. 3. Spatial grid used for the computations. We have for the temporal grid, in the unidimensional case for example u n + 1 = a u n +, b, h, n n +1 n +1 n h = c u + d h u , V and h are computed at the same moment, but in the computation of h , esti­ mated values of u and v are used. All the boundaries are walls, and the normal velocity is assumed equal to zero at the coast. All calculations are done with a constant grid resolution of 50 km in both x and y directions. The stability condition At At < 1 Ax Ay requires At to be < 18 248 s (about 5 h) . The chosen temporal step was At = 3 h 104 (1/8 day). Other constants are : H 0 = 50 m ; A = IO2 m2s -1 ; g' = 2 x IO-2 m s -1 ; 3 = 2 x io'11 nf 1s“ 1 . Since we are interested in studying the probable effect of the irregular coastline geometry on the upwelling generation, evolution and intensification, we have chosen to study two major aspects : - the first one with prominent coastline features such as Cape Palmas, Cape Three Points, Cape Formoso and Cape Lopez; - the second, for comparison, with a linear coastline for the west african coast. For both cases, two situations are investigated : 1.3.1. a standard linear situation with an increase of respectively 0.025 Nm and 0.0125 N m 2 in the westward wind stress over the western 1 500 km of the basin (fig. 4) and without any meridional wind; 0 1 2 3 4 5 Distance km x 10 3 0 - 1 5 - 20 - Fig. 4. Spatial variation of the zonal wind stress. 1.3.2. a second situation, non linear, similar to the first but including advec- tive effects, local depth in the stress term, non-linearities in the continuity equa­ tion and an increase of 0.0125 N m -2 of the westward wind stress. In each situation, integrations are performed at least over 90 days, starting from rest (u = v = 0 at t = 0), with a sudden increase of wind stress (fig. 5) remaining constant throughout the following period of integration. To allow an easy comparison of the results, we have used the same denomination fo boundaries as did Adamec and O'Brien (1978) : the eastern boundary extending 500 km north of the Equator and 1500 km south is the south-eastern (S-eastern) boundary; the eastern boundary extending 500 km north of the Equator to 1500 km is the north­ eastern (N-eastern) boundary; the northern boundary is then the northern boundary of the Gulf of Guinea, extending approximately from Cape Palmas to Cape Formoso, i.e. r 105 ■i f 0 0 10 20 30 40 50 60 70 80 90 Days Fig. 5. Temporal variation of the wind stress. from 3 000 to 5 000 km east of the western boundary; the north-northern (N-northern) boundary is the northern boundary of the basin extending 3 000 km from the western boundary (fig.
Load more

Recommended publications
  • Addressing the Atlantic's Emerging Security Challenges
    34 Addressing the Atlantic’s Emerging Security Challenges Bruno Lété The German Marshall Fund of the United States ABSTRACT As the Atlantic space is expected to continue to play a global role, it is not surprising that nations around the Atlantic have become increasingly concerned about securing the region’s commons at land, at sea, and in the air. In much contrast to the territorial disputes and military tensions defining the Pacific Rim, the Atlantic remains a relatively stable geo-political sphere, largely due to the lack of great power conflict. But the prominence of the region in security and military considerations is rising, especially with the aim to combat illegal activities. This paper identifies three emerging security challenges that may jeopardize the future peace and prosperity of all the countries surrounding the Atlantic Ocean if they are left unresolved. The first draft of this Scientific Paper was presented at the ATLANTIC FUTURE Seminar, Lisbon, 24 April 2015 ATLANTIC FUTURE SCIENTIFIC PAPER 34 Table of contents 1. Introduction ..................................................................................................... 3 2. The Atlantic remains a key region in a rapidly changing global system ...................................................................................................... 3 3. Three emerging challenges affect security in the Atlantic ....... 4 4. A pan-Atlantic approach is lacking ...................................................... 9 5. Conclusion ..................................................................................................
    [Show full text]
  • Fronts in the World Ocean's Large Marine Ecosystems. ICES CM 2007
    - 1 - This paper can be freely cited without prior reference to the authors International Council ICES CM 2007/D:21 for the Exploration Theme Session D: Comparative Marine Ecosystem of the Sea (ICES) Structure and Function: Descriptors and Characteristics Fronts in the World Ocean’s Large Marine Ecosystems Igor M. Belkin and Peter C. Cornillon Abstract. Oceanic fronts shape marine ecosystems; therefore front mapping and characterization is one of the most important aspects of physical oceanography. Here we report on the first effort to map and describe all major fronts in the World Ocean’s Large Marine Ecosystems (LMEs). Apart from a geographical review, these fronts are classified according to their origin and physical mechanisms that maintain them. This first-ever zero-order pattern of the LME fronts is based on a unique global frontal data base assembled at the University of Rhode Island. Thermal fronts were automatically derived from 12 years (1985-1996) of twice-daily satellite 9-km resolution global AVHRR SST fields with the Cayula-Cornillon front detection algorithm. These frontal maps serve as guidance in using hydrographic data to explore subsurface thermohaline fronts, whose surface thermal signatures have been mapped from space. Our most recent study of chlorophyll fronts in the Northwest Atlantic from high-resolution 1-km data (Belkin and O’Reilly, 2007) revealed a close spatial association between chlorophyll fronts and SST fronts, suggesting causative links between these two types of fronts. Keywords: Fronts; Large Marine Ecosystems; World Ocean; sea surface temperature. Igor M. Belkin: Graduate School of Oceanography, University of Rhode Island, 215 South Ferry Road, Narragansett, Rhode Island 02882, USA [tel.: +1 401 874 6533, fax: +1 874 6728, email: [email protected]].
    [Show full text]
  • Coastal Processes and Longshore Sediment Transport Along Krui Coast, Pesisir Barat of Lampung
    ICOSITER 2018 Proceeding Journal of Science and Applicative Technology Coastal Processes and Longshore Sediment Transport along Krui Coast, Pesisir Barat of Lampung Trika Agnestasia Tarigan 1, Nanda Nurisman 1 1 Ocean Engineering Department, Institut Teknologi Sumatera, Lampung Selatan, Lampung Abstract. Longshore sediment transport is one of the main factors influencing coastal geomorphology along the Krui Coast, Pesisir Barat of Lampung. Longshore sediment transport is closely related to the longshore current that is generated when waves break obliquely to the coast. The growth of waves depends upon wind velocity, the duration of the wind, and the distance over which the wind blow called fetch. The daily data of wind speed and direction are forecast from European Centre for Medium-Range Weather Forecasts (ECMWF). This study examines for predicting longshore sediment transport rate using empirical method. The wave height and period were calculated using Shore Protection Manual (SPM) 1984 method and the longshore sediment transport estimation based on the CERC formula, which also includes the wave period, beach slope, sediment grain size, and breaking waves type. Based on the use CERC formula it is known that from the Southeast direction (Qlst(1) ) the sediment transport discharge is 2.394 m3/s, in 1 (one) year the amount of sediment transport reaches 75,495,718 m3/s. 3 Whereas from the northwest direction of (Qlst(2)) the sediment transport debit is 2.472 m /s, in 1 (one) year the amount of sediment transport reaches 77,951,925 m3/s. 1. Introduction The geographical condition of Krui Coast which is directly adjacent to the Indian Ocean makes this area get a direct influence from the physical parameters of the sea, which is the wave.
    [Show full text]
  • Wintertime Coastal Upwelling in Lake Geneva: an Efficient Transport
    RESEARCH ARTICLE Wintertime Coastal Upwelling in Lake Geneva: An 10.1029/2020JC016095 Efficient Transport Process for Deepwater Key Points: • Coastal upwelling during winter in a Renewal in a Large, Deep Lake large deep lake was investigated by Rafael S. Reiss1 , U. Lemmin1, A. A. Cimatoribus1 , and D. A. Barry1 field observations, 3‐D numerical modeling, and particle tracking 1Ecological Engineering Laboratory (ECOL), Faculty of Architecture, Civil and Environmental Engineering (ENAC), • Upwelled water masses originating from the deep hypolimnion spend Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland up to 5 days near the surface before descending back into that layer • Wintertime coastal upwelling is an Abstract Combining field measurements, 3‐D numerical modeling, and Lagrangian particle tracking, fi ef cient yet overlooked process for we investigated wind‐driven, Ekman‐type coastal upwelling during the weakly stratified winter period deepwater renewal in large deep lakes with favorable wind conditions 2017/2018 in Lake Geneva, Western Europe's largest lake (max. depth 309 m). Strong alongshore wind stress, persistent for more than 7 days, led to tilting and surfacing of the thermocline (initial depth Supporting Information: 75–100 m). Observed nearshore temperatures dropped by 1°C and remained low for 10 days, with the lowest • Supporting Information S1 temperatures corresponding to those of hypolimnetic waters originating from 200 m depth. Nearshore • Movie S1 current measurements at 30 m depth revealed dominant alongshore currents in the entire water column − (maximum current speed 25 cm s 1) with episodic upslope transport of cold hypolimnetic waters in the fi ‐ Correspondence to: lowest 10 m mainly during the rst 3 days.
    [Show full text]
  • Coastal Dynamics 2017 Paper No. 156 513 How Tides and Waves
    Coastal Dynamics 2017 Paper No. 156 How Tides and Waves Enhance Aeolian Sediment Transport at The Sand Motor Mega-nourishment , 1,2 1 1 Bas Hoonhout1 2, Arjen Luijendijk , Rufus Velhorst , Sierd de Vries and Dano Roelvink3 Abstract Expanding knowledge concerning the close entanglement between subtidal and subaerial processes in coastal environments initiated the development of the open-source Windsurf modeling framework that enables us to simulate multi-fraction sediment transport due to subtidal and subaerial processes simultaneously. The Windsurf framework couples separate model cores for subtidal morphodynamics related to waves and currents and storms and aeolian sediment transport. The Windsurf framework bridges three gaps in our ability to model long-term coastal morphodynamics: differences in time scales, land/water boundary and differences in meshes. The Windsurf framework is applied to the Sand Motor mega-nourishment. The Sand Motor is virtually permanently exposed to tides, waves and wind and is consequently highly dynamic. In order to understand the complex morphological behavior of the Sand Motor, it is vital to take both subtidal and subaerial processes into account. The ultimate aim of this study is to identify governing processes in aeolian sediment transport estimates in coastal environments and improve the accuracy of long-term coastal morphodynamic modeling. At the Sand Motor beach armoring occurs on the dry beach. In contrast to the dry beach, no armor layer can be established in the intertidal zone due to periodic flooding. Consequently, during low tide non-armored intertidal beaches are susceptible for wind erosion and, although moist, may provide a larger aeolian sediment supply than the vast dry beach areas.
    [Show full text]
  • Evolution of Spectra for Mechanical and Wind Waves in a Large Tank
    V. Polnikov, F. Qiao, H. Ma, and S. Jiang EVOLUTION OF SPECTRA FOR MECHANICAL AND WIND WAVES IN A LARGE TANK Vladislav Polnikov1†1, Fangli Qiao2, 3, Hongyu Ma2, and Shumin Jiang2 1A.M. Obukhov Institute of Atmospheric Physics of RAS, Moscow, Russia 2First Institute of Oceanography of MNR, Qingdao, China 3Laboratory for Regional Oceanography and Numerical Modeling, Qingdao National Laboratory for Marine Science and Technology, Qingdao, China (Received xx; revised xx; accepted xx) Empirical spectra for mechanical and wind waves measured in a large tank of the First Institute of Oceanography of China are presented. Analysis for the first and the second type of waves is done separately. It is shown that, in the case of mechanical waves with a steepness more than 0.2, the frequency spectra of waves evolve to ones with the tail decay S() f f 4.2 0.1 , whilst the shape of spectra at large fetches is self-similar. Numerical solutions of the four-wave kinetic equation, written in the fetch-limited version, result in the same spectra. This allows treating the empirical observations for mechanical waves as the natural evolution of free nonlinear surface waves. In the case of wind waves, the wave spectra evolve to ones with the tail decay S() f f 4.0 0.05 at fetches X greater than 8 meters, under any applied winds. The well-known 3/2 Toba’s “three-second relation”, HT p , between the mean wave height, H, and the peak period, Tp, is well fulfilled. Though, the intensities of spectra tails do not follow the Toba’s ratio, 4 24p S()() f gu* f , rather they better correspond to the ratio S()(/)() f u** Xg gu f with p = 1/3.
    [Show full text]
  • Waves and Structures
    WAVES AND STRUCTURES By Dr M C Deo Professor of Civil Engineering Indian Institute of Technology Bombay Powai, Mumbai 400 076 Contact: [email protected]; (+91) 22 2572 2377 (Please refer as follows, if you use any part of this book: Deo M C (2013): Waves and Structures, http://www.civil.iitb.ac.in/~mcdeo/waves.html) (Suggestions to improve/modify contents are welcome) 1 Content Chapter 1: Introduction 4 Chapter 2: Wave Theories 18 Chapter 3: Random Waves 47 Chapter 4: Wave Propagation 80 Chapter 5: Numerical Modeling of Waves 110 Chapter 6: Design Water Depth 115 Chapter 7: Wave Forces on Shore-Based Structures 132 Chapter 8: Wave Force On Small Diameter Members 150 Chapter 9: Maximum Wave Force on the Entire Structure 173 Chapter 10: Wave Forces on Large Diameter Members 187 Chapter 11: Spectral and Statistical Analysis of Wave Forces 209 Chapter 12: Wave Run Up 221 Chapter 13: Pipeline Hydrodynamics 234 Chapter 14: Statics of Floating Bodies 241 Chapter 15: Vibrations 268 Chapter 16: Motions of Freely Floating Bodies 283 Chapter 17: Motion Response of Compliant Structures 315 2 Notations 338 References 342 3 CHAPTER 1 INTRODUCTION 1.1 Introduction The knowledge of magnitude and behavior of ocean waves at site is an essential prerequisite for almost all activities in the ocean including planning, design, construction and operation related to harbor, coastal and structures. The waves of major concern to a harbor engineer are generated by the action of wind. The wind creates a disturbance in the sea which is restored to its calm equilibrium position by the action of gravity and hence resulting waves are called wind generated gravity waves.
    [Show full text]
  • Coastal Risk Assessment for Ebeye
    Coastal Risk Assesment for Ebeye Technical report | Coastal Risk Assessment for Ebeye Technical report Alessio Giardino Kees Nederhoff Matthijs Gawehn Ellen Quataert Alex Capel 1230829-001 © Deltares, 2017, B De tores Title Coastal Risk Assessment for Ebeye Client Project Reference Pages The World Bank 1230829-001 1230829-00 1-ZKS-OOO1 142 Keywords Coastal hazards, coastal risks, extreme waves, storm surges, coastal erosion, typhoons, tsunami's, engineering solutions, small islands, low-elevation islands, coral reefs Summary The Republic of the Marshall Islands consists of an atoll archipelago located in the central Pacific, stretching approximately 1,130 km north to south and 1,300 km east to west. The archipelago consists of 29 atolls and 5 reef platforms arranged in a double chain of islands. The atolls and reef platforms are host to approximately 1,225 reef islands, which are characterised as low-lying with a mean elevation of 2 m above mean sea leveL Many of the islands are inhabited, though over 74% of the 53,000 population (2011 census) is concentrated on the atolls of Majuro and Kwajalein The limited land size of these islands and the low-lying topographic elevation makes these islands prone to natural hazards and climate change. As generally observed, small islands have low adaptive capacity, and the adaptation costs are high relative to the gross domestic product (GDP). The focus of this study is on the two islands of Ebeye and Majuro, respectively located on the Ralik Island Chain and the Ratak Island Chain, which host the two largest population centres of the archipelago.
    [Show full text]
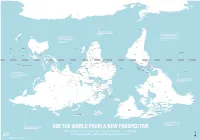
  • Is Map Is Just As Accurate As the One We're All Used To
    ROSS SEA WEDDELL SEA AMUNDSEN SEA ANTARCTICA BELLINGSHAUSEN SEA AMERY ICE SHELF SOUTHERN OCEAN SOUTHERN OCEAN SOUTHERN OCEAN SCOTIA SEA DRAKE PASSAGE FALKLAND ISLANDS Stanley (U.K.) THE RATIO OF LAND TO WATER IN THE SOUTHERN HEMISPHERE BY THE TIME EUROPEANS ADOPTED IS 1 TO 5 THE NORTH-POINTING COMPASS, PTOLEMY WAS A HELLENIC Wellington THEY WERE ALREADY EXPERIENCED NEW TASMAN SEA ZEALAND CARTOGRAPHER WHOSE WORK CHILE IN NAVIGATING WITH REFERENCE TO IN THE SECOND CENTURY A.D. ARGENTINA THE NORTH STAR Canberra Buenos Santiago GREAT AUSTRALIAN BIGHT POPULARIZED NORTH-UP Montevideo Aires SOUTH PACIFIC OCEAN SOUTH ATLANTIC OCEAN URUGUAY ORIENTATION SOUTH AFRICA Maseru LESOTHO SWAZILAND Mbabane Maputo Asunción AUSTRALIA Pretoria Gaborone NEW Windhoek PARAGUAY TONGA Nouméa CALEDONIA BOTSWANA Saint Denis NAMIBIA Nuku’Alofa (FRANCE) MAURITIUS Port Louis Antananarivo MOZAMBIQUE CHANNEL ZIMBABWE Suva Port Vila MADAGASCAR VANUATU MOZAMBIQUE Harare La Paz INDIAN OCEAN Brasília LAKE SOUTH PACIFIC OCEAN FIJI Lusaka TITICACA CORAL SEA GREAT GULF OF BARRIER CARPENTARIA Lilongwe ZAMBIA BOLIVIA FRENCH POLYNESIA Apia REEF LAKE (FRANCE) SAMOA TIMOR SEA COMOROS NYASA ANGOLA Lima Moroni MALAWI Honiara ARAFURA SEA BRAZIL TIMOR LESTE PERU Funafuti SOLOMON Port Dili Luanda ISLANDS Moresby LAKE Dodoma TANGANYIKA TUVALU PAPUA Jakarta SEYCHELLES TANZANIA NEW GUINEA Kinshasa Victoria BURUNDI Bujumbura DEMOCRATIC KIRIBATI Brazzaville Kigali REPUBLIC LAKE OF THE CONGO SÃO TOMÉ Nairobi RWANDA GABON ECUADOR EQUATOR INDONESIA VICTORIA REP. OF AND PRINCIPE KIRIBATI EQUATOR
    [Show full text]
  • 195 the Gulf of Guinea
    THE GULF OF GUINEA: THE NEW DANGER ZONE Africa Report N°195 – 12 December 2012 Translation from French TABLE OF CONTENTS EXECUTIVE SUMMARY AND RECOMMENDATIONS ................................................. i I. INTRODUCTION ............................................................................................................. 1 II. A STRATEGIC REGION IN THE GRIP OF INSECURITY ...................................... 2 A. RENEWED STRATEGIC INTEREST IN NATURAL RESOURCES .......................................................... 2 B. A CONTEXT FAVOURABLE TO MARITIME CRIME ......................................................................... 3 C. WEAK MARITIME POLICIES .......................................................................................................... 4 III. NIGERIA: EPICENTRE OF VIOLENCE AT SEA ...................................................... 6 A. POOR GOVERNANCE AND MARITIME CRIME ................................................................................ 6 1. A leaky oil sector ......................................................................................................................... 6 2. The rise in economic crime .......................................................................................................... 7 3. State capacity hampered by corruption ........................................................................................ 8 4. The Niger Delta ...........................................................................................................................
    [Show full text]
  • 4 European Policy and Energy Interests – Challenges from the Gulf of Guinea ␣
    CHAPTER I OIL POLICY IN THE GULF OF GUINEA 4 European Policy and Energy Interests – Challenges from the Gulf of Guinea ␣ By Lutz Neumann 1. Introduction ␣ The Gulf of Guinea has great oil and gas potential. While predictions on Africa should be made with some care, analysts and representatives of the oil industry appear to agree that the region belongs to those areas where production will rapidly increase in the coming years and decades. Output figures of the chief oil- producing countries, Nigeria and Angola, are expected to double or triple within the next decade and thus will cause certain dynamics on the shaping of trade movements (see table 1). Table 1: Projected Oil Production of Gulf of Guinea 2005-2030 (in b/d) 2005 2010 2015 2030 Nigeria 2,719,000 3,042,000 3,729,000 4,422,000 Angola 1,098,000 2,026,000 2,549,000 3,288,000 Equatorial-Guinea 313,000 466,000 653,000 724,000 Congo (Brazzaville) 285,000 300,000 314,000 327,000 Gabon 303,000 291,000 279,000 269,000 Côte d’Ivoire 43,000 71,000 83,000 94,000 Cameroun 84,000 72,000 66,000 61,000 Congo (Kinshasa) 30,000 33,000 30,000 25,000 Ghana 11,000 16,000 20,000 23,000 Total Africa 9,936,000 12,059,000 13,975,000 16,242,000 Source: EIA, U.S. Department of Energy.␣ FRIEDRICH-EBERT-STIFTUNG 59 OIL POLICY IN THE GULF OF GUINEA CHAPTER I The African countries along the Atlantic coast represent a growing supplier region.
    [Show full text]
  • Influence of the Gulf of Guinea Coastal and Equatorial Upwellings on the Precipitations Along Its Northern Coasts During the Boreal Summer Period
    Asian Journal of Applied Sciences 4 (3): 271-285, 2011 ISSN 1996-3343 I DOI: 10.3923/ajaps.2011.271.285 © 2011 Knowledgia Review, Malaysia Influence of the Gulf of Guinea Coastal and Equatorial Upwellings on the Precipitations along its Northern Coasts during the Boreal Summer Period 'K.E. Ali, 'K.Y. Kouadio, 'E.-P. Zahiri, 'A. Aman, 'A.P. Assamoi and 2B. Bourles 'LAPAMF, Universite de Cocody-Abidjan BP 231 Abidjan, Cote d'Ivoire 2IRD/LEGOS-CRHOB, Representation !RD, 08 BP 841 Cotonou, Republique du Benin Corresponding Author: Angora Aman, Universite de Cocody-Abidjan 22 BP 582 Abidjan 22, LAPA-MF, UFR-SSMT, Cote d'Ivoire Tel: (225) 07 82 77 52 Fax: (225) 22 44 14 07 ABSTRACT The Gulf of Guinea (GG) is an area where a seasonal upwelling takes place, along the equator and its northern coasts between Benin and Cote d'Ivoire. The coastal upwelling has a real impact on the local yet documented biological resources. However, climatic impact studies of this seasonal upwelling are paradoxically very rare and disseminated and this impact is still little known, especially on the potential part played by the upwelling onset on the regional precipitation in early boreal summer. This study shows that coastal precipitations of the July-September period are correlated by both the coastal and equatorial sea-surface temperatures (SSTS). This correlation results in a decrease or a rise of rainfall when the SSTs are abnormally cold or warm respectively. The coastal areas that are more subject to coastal and equatorial SSTs influence are located around the Cape Three Points, where the coastal upwelling exhibits the maximum of amplitude.
    [Show full text]