Computer Simulation of Polymer Chain Statistics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![[Bus] Meguro-Dori T Okyu Meguro Line JR Y Amanote Line Y Amate-Dori Meguro Station Access](https://docslib.b-cdn.net/cover/7153/bus-meguro-dori-t-okyu-meguro-line-jr-y-amanote-line-y-amate-dori-meguro-station-access-287153.webp)
[Bus] Meguro-Dori T Okyu Meguro Line JR Y Amanote Line Y Amate-Dori Meguro Station Access
To Shibuya To Meguroshinbashi Ootorijinjamae Mos Burger Meguro-dori West exit Meguro Maruetsu Police Station Ootori shrine box My Basket drug store RECODS Liquor Seven-eleven West exit shop Gyoninzaka The 4th parking lot (Toll parking, Rakan reservation is needed.) ⑨ Meguro Gajoen Front entrance *Refer to attached map Temple Meguro Arco Tower Station Atre Naboku Line Sunkus Mita Line Rakan Tokyu Meguro Line Kaikan Megurofudo The 3rd parking lot Meguro Line Tokyu Line JR Yamanote The 2nd parking lot (Toll parking, Kinokuniya reservation is needed.) HQ Daikokuya Megurofudosonmae dori Kamurozakashita Super Ozeki Yamate-dori Matsuya Florist's Shinagawa To Fudomae Station Access [Bus] A short walk from “Fudoson Sando” bus stop of Route Shibuya 41 [Train] bound for Ooimachi Station of Tokyu Bus. 10 minute walk from JR/Tokyo Metro Meguro Station (Please take Tokyu Bus from the south exit of Shibuya Station 7 minute walk from Tokyu Line Fudomae Station. or from Tokyu Toyoko Line Nakameguro Station.) [IMAGE STUDIO 109, INC 2-24-12, Shimomeguro, Meguro-ku, Tokyo, 153-0064 (MEGURO CUE building) Studio department Post production department □CCTV department General affairs department TEL.03-5436-9109 FAX.03-3494-8871 Parking lot guide To Nakameguro Ootorijinjamae Meguro-dori Meguroshinbashi Maruetsu Ootori shrine Yamate-dori drug store RECODS Yanagi-dori Meguro River Rakan Temple Sunkus The 3rd parking lot (Reservation is needed.) The 3rd parking lot *Refer to attached map (Reservation is needed.) Multistory car park Megurofudo Daikokuya Kinokuniya HQ The 2nd parking lot To Gotanda [About parking lots] If all the parking lots shown above are full, please use other parking facilities nearby. -

Meguro Walking Map
Meguro Walking Map Meguro Walking Map Primary print number No. 31-30 Published February 2, 2020 December 6, 2019 Published by Meguro City Edited by Health Promotion Section, Health Promotion Department; Sports Promotion Section, Culture and Sports Department, Meguro City 2-19-15 Kamimeguro, Meguro City, Tokyo Phone 03-3715-1111 Cooperation provided by Meguro Walking Association Produced by Chuo Geomatics Co., Ltd. Meguro City Total Area Course Map Contents Walking Course 7 Meguro Walking Courses Meguro Walking Course Higashi-Kitazawa Sta. Total Area Course Map C2 Walking 7 Meguro Walking Courses P2 Course 1: Meguro-dori Ave. Ikenoue Sta. Ke Walk dazzling Meguro-dori Ave. P3 io Inok Map ashira Line Komaba-todaimae Sta. Course 2: Komaba/Aobadai area Shinsen Sta. Walk the ties between Meguro and Fuji P7 0 100 500 1,000m Awas hima-dori St. 3 Course 3: Kakinokizaka/Higashigaoka area Kyuyamate-dori Ave. Walk the 1964 Tokyo Olympics P11 2 Komaba/Aobadai area Walk the ties between Meguro and Fuji Shibuya City Tamagawa-dori Ave. Course 4: Himon-ya/Meguro-honcho area Ikejiri-ohashi Sta. Meguro/Shimomeguro area Walk among the history and greenery of Himon-ya P15 5 Walk among Edo period townscape Daikan-yama Sta. Course 5: Meguro/Shimomeguro area Tokyu Den-en-toshi Line Walk among Edo period townscape P19 Ebisu Sta. kyo Me e To tro Hibiya Lin Course 6: Yakumo/Midorigaoka area Naka-meguro Sta. J R Walk a green road born from a culvert P23 Y Yutenji/Chuo-cho area a m 7 Yamate-dori Ave. a Walk Yutenji and the vestiges of the old horse track n o Course 7: Yutenji/Chuo-cho area t e L Meguro City Office i Walk Yutenji and the vestiges of the old horse track n P27 e / S 2 a i k Minato e y Kakinokizaka/Higashigaoka area o in City Small efforts, L Yutenji Sta. -

Huge City Model Communicates the Appeal of Tokyo -To Be Used by City in Presentation Given to IOC Evaluation Commission
Press Release 2009-04-17 Mori Building Co., Ltd. Mori Building provides support for Olympic and Paralympic bid Huge city model communicates the appeal of Tokyo -To be used by city in presentation given to IOC Evaluation Commission- At 17.0 m × 15.3 m, Japan's largest model With Tokyo making a bid to host the 2016 Olympic and Paralympic Games, Mori Building is cooperating with the city by providing a huge model of central Tokyo for use in the upcoming tour of the IOC Evaluation Commission. This model was created with original technology developed by Mori Building; it is on display at Tokyo Big Sight. Created at 1/1000 scale, the model incorporates Olympic-related facilities that would be constructed in the city, and it presents a very appealing and sophisticated representation of near-future Tokyo. The model's 17.0 m × 15.3 m size makes it the largest in Japan, and its fine detail and high impact communicate a very real and attractive picture of Tokyo. On public view until April 30 In support of the Tokyo Olympic and Paralympic bid, Mori Building is providing this city model as a tool that visually communicates the city's appeal in an easy-to-understand manner. From April 17 afternoon to 30, the model will be on display to the public in the Tokyo Big Sight entrance hall. We hope that many members of the general public will see it, and that it will further increase their interest in Tokyo. Mori Building independently created city model/CG pictures as a tool to facilitate an objective and panoramic comprehension of the city/landscape. -
Introducing Tokyo Page 10 Panorama Views
Introducing Tokyo page 10 Panorama views: Tokyo from above 10 A Wonderful Catastrophe Ulf Meyer 34 The Informational World City Botond Bognar 42 Bunkyo-ku page 50 001 Saint Mary's Cathedral Kenzo Tange 002 Memorial Park for the Tokyo War Dead Takefumi Aida 003 Century Tower Norman Foster 004 Tokyo Dome Nikken Sekkei/Takenaka Corporation 005 Headquarters Building of the University of Tokyo Kenzo Tange 006 Technica House Takenaka Corporation 007 Tokyo Dome Hotel Kenzo Tange Chiyoda-ku page 56 008 DN Tower 21 Kevin Roche/John Dinkebo 009 Grand Prince Hotel Akasaka Kenzo Tange 010 Metro Tour/Edoken Office Building Atsushi Kitagawara 011 Athénée Français Takamasa Yoshizaka 012 National Theatre Hiroyuki Iwamoto 013 Imperial Theatre Yoshiro Taniguchi/Mitsubishi Architectural Office 014 National Showa Memorial Museum/Showa-kan Kiyonori Kikutake 015 Tokyo Marine and Fire Insurance Company Building Kunio Maekawa 016 Wacoal Building Kisho Kurokawa 017 Pacific Century Place Nikken Sekkei 018 National Museum for Modern Art Yoshiro Taniguchi 019 National Diet Library and Annex Kunio Maekawa 020 Mizuho Corporate Bank Building Togo Murano 021 AKS Building Takenaka Corporation 022 Nippon Budokan Mamoru Yamada 023 Nikken Sekkei Tokyo Building Nikken Sekkei 024 Koizumi Building Peter Eisenman/Kojiro Kitayama 025 Supreme Court Shinichi Okada 026 Iidabashi Subway Station Makoto Sei Watanabe 027 Mizuho Bank Head Office Building Yoshinobu Ashihara 028 Tokyo Sankei Building Takenaka Corporation 029 Palace Side Building Nikken Sekkei 030 Nissei Theatre and Administration Building for the Nihon Seimei-Insurance Co. Murano & Mori 031 55 Building, Hosei University Hiroshi Oe 032 Kasumigaseki Building Yamashita Sekkei 033 Mitsui Marine and Fire Insurance Building Nikken Sekkei 034 Tajima Building Michael Graves Bibliografische Informationen digitalisiert durch http://d-nb.info/1010431374 Chuo-ku page 74 035 Louis Vuitton Ginza Namiki Store Jun Aoki 036 Gucci Ginza James Carpenter 037 Daigaku Megane Building Atsushi Kitagawara 038 Yaesu Bookshop Kajima Design 039 The Japan P.E.N. -

Construction of the “Meguro-Ku Aobadai Project” (Tentative Name) Begins
January 21, 2021 Press Team: Developing Income-generating Real Estate by Leveraging the Mitsubishi Corporation Group’s Overseas Network Construction of the “Meguro-ku Aobadai Project” (Tentative Name) Begins Mitsubishi Corporation Urban Development, Inc. (MCUD1) is pleased to announce that on January 21, 2021, construction began in Aobadai, Meguro-ku, Tokyo, on the “Meguro-ku Aobadai Project” (tentative name), a rental housing development project. This project will be developed as part of its PRE support2 for foreign clients. MCUD will continue to engage in the development business, in order to provide the market with quality income-generating real estate that 2 meets the needs of investors, by making full use of its CRE/PRE support , in addition to its development know-how regarding income-generating real estate, as well as the domestic and overseas networks and information capabilities of the Mitsubishi Corporation Group. 1: Headquarters: Chiyoda-ku, Tokyo; Representative: Hiroki Itokawa 2: PRE support: Support for the effective use of “Public Real Estate” CRE support: Support for the effective use of “Corporate Real Estate” ■ Overview of Development (1) Location The property is conveniently located within walking distance of Daikanyama Station on the Tokyu Toyoko Line, as well as Nakameguro Station on the Tokyu Toyoko Line and Tokyo Metro Hibiya Line. It is situated in one of Japan’s leading residential areas with a sophisticated streetscape unique to the Daikanyama area, and in a rare location that provides a concentration of facilities typifying the surrounding area. (2) Facility Plans The rental housing complex is for high-income earners with a total of 19 units, two stories above ground and four below, making the most of the characteristic slope on the southern side of the building, with the main approach retaining the rich natural scenery of the old Yamate Street. -

Railway Lines in Tokyo and Its Suburbs
Minami-Sakurai Hasuta Shin-Shiraoka Fujino-Ushijima Shimizu-Koen Railway Lines in Tokyo and its Suburbs Higashi-Omiya Shiraoka Kuki Kasukabe Kawama Nanakodai Yagisaki Obukuro Koshigaya Atago Noda-Shi Umesato Unga Edogawadai Hatsuisi Toyoshiki Fukiage Kita-Konosu JR Takasaki Line Okegawa Ageo Ichinowari Nanasato Iwatsuki Higashi-Iwatsuki Toyoharu Takesato Sengendai Kita-Koshigaya Minami-Koshigaya Owada Tobu-Noda Line Kita-Kogane Kashiwa Abiko Kumagaya Gyoda Konosu Kitamoto Kitaageo Tobu Nota Line Toro Omiya-Koen Tennodai Miyahara Higashi-Urawa Higashi-Kawaguchi JR Musashino Line Misato Minami-Nagareyama Urawa Shin-Koshigaya Minami- Kita- Saitama- JR Tohoku HonsenKita-Omiya Warabi Nishi-Kawaguchi Kawaguchi Kashiwa Kashiwa Hon-Kawagoe Matsudo Shin- Gamo Takenozuka Yoshikawa Shin-Misato Shintoshin Nishi-Arai Umejima Mabashi Minoridai Gotanno Yono Kita-Urawa Minami-Urawa Kita-Akabane Akabane Shinden Yatsuka Shin- Musashiranzan Higashi-Jujo Kita-Matsudo Shinrin-koenHigashi-MatsuyamaTakasaka Omiya Kashiwa Toride Yono Minami- Honmachi Yono- Matsubara-Danchi Shin-Itabashi Minami-FuruyaJR Kawagoe Line Musashishi-Urawa Kita-Toda Toda Toda-Koen Ukima-Funato Kosuge JR Saikyo Line Shimo Matsudo Kita-Sakado Kita- Shimura- Akabane-Iwabuchi Soka Masuo Ogawamachi Naka-Urawa Takashimadaira Shiden Matsudo- Yono Nishi-Takashimadaira Hasune Sanchome Itabashi-Honcho Oji Kita-senju Kami- Myogaku Sashiogi Nisshin Nishi-Urawa Daishimae Tobu Isesaki Line Kita-Ayase Kanamachi Hongo Shimura- Jujo Oji-Kamiya Oku Sakasai Yabashira Kawagoe Shingashi Fujimino Tsuruse -

Moderation of Summertime Heat-Island Phenomena Via
ICUC9 - 9th International Conference on Urban Climate jointly with 12th Symposium on the Urban Environment Moderation of summertime heat-island phenomena via modification of the urban form in the Tokyo metropolitan area Sachiho A. Adachi1, Fujio Kimura2, Hiroyuki Kusaka2, Michael G. Duda3, Yoshiki Yamagata4, Hajime Seya4,5, Kumiko Nakamichi4,6, and Toshinori Aoyagi7 1 Advanced Institute for Computational Science, RIKEN, 7-1-26 Minatojima-minamimachi Cyuoku, Kobe, Japan, [email protected] 2 Center for Computational Sciences, University of Tsukuba,1-1-1 Tennoudai, Tsukuba, Japan 3 National Center for Atmospheric Research, 3090 Center Green Drive, Boulder, Colorado, USA 4 National Institute for Environmental Studies, 16-2 Onogawa, Tsukuba, Japan 5 Hiroshima University, 1-3-2 Kagamiyama, Higashi-Hiroshima, Japan 6 Tokyo Institute of Technology, 2-12-1 Ookayama Meguro-ku, Tokyo, Japan 7 Meteorological Research Institute, 1-1 Nagamine, Tsukuba, Japan dated : 15 Jun 2015 1. Introduction Moderation of the urban heat island is expected to become part of an adaptation strategy to global climate change because urban heat-island mitigation should be mostly implemented by local governments (e.g. Adachi et al. 2012). Many methods have been proposed to mitigate urban heat-island effects, such as changes in the urban form, greening of parking lots and building walls, increasing roof albedo, and changes in pavement materials. This study focused on changes in urban form and investigated the moderation of nighttime surface air temperatures in the Tokyo metropolitan area (TMA) through simulations of dispersed- and compact-city scenarios at the current population level. This study has been published in Journal of Applied Meteorology and Climatology. -
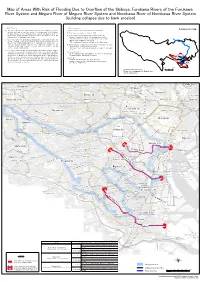
Map of Areas with Risk of Flooding Due to Overflow of the Shibuya
Map of Areas With Risk of Flooding Due to Overflow of the Shibuya, Furukawa Rivers of the Furukawa River System and Meguro River of Meguro River System and Nomikawa River of Nomikawa River System (building collapse due to bank erosion) 1. About this map 2. Basic information Location map (1) This map shows the areas where there may be flooding powerful enough to (1) Map created by the Tokyo Metropolitan Government collapse buildings for sections subject to flood warnings of the Shibuya, (2) Risk areas designated on June 27, 2019 Furukawa Rivers of the Furukawa River System and Meguro River of Meguro River System and those subject to water-level notification of the (3) River subject to flood warnings covered by this map Nomikawa River of Nomikawa River System. Shibuya, Furukawa Rivers of the Furukawa River System (The flood warning section is shown in the table below.) (2) This river flood risk map shows estimated width of bank erosion along the Meguro River of Meguro River System Shibuya, Furukawa rivers of the Furukawa River System and Meguro River of (The flood warning section is shown in the table below.) Meguro River System and Nomikawa River of Nomikawa River System resulting from the maximum assumed rainfall. The simulation is based on the (4) Rivers subject to water-level notification covered by this map Sumida River situation of the river channels and flood control facilities as of the Nomikawa River of Nomikawa River System time of the map's publication. (The water-level notification section is shown in the table below.) (3) This river flood risk map (building collapse due to bank erosion) roughly indicates the areas where buildings could collapse or be washed away when (5) Assumed rainfall the banks of the Shibuya, Furukawa Rivers of the Furukawa River System and Up to 153mm per hour and 690mm in 24 hours in the Shibuya, Meguro River of Meguro River System and Nomikawa River of Nomikawa River Furukawa, Meguro, Nomikawa Rivers basin Shibuya River,Furukawa River System are eroded. -

Bonus 2: International Schools the One & Only Guide You Need Tokyo Expat Job Search Guide
Bonus 2: International Schools The One & Only Guide You Need Tokyo Expat Job Search Guide Bonus 2: International Schools RAINER MORITA BONUS 2 INTERNATIONAL SCHOOLS Below you find a list of international schools for your children: American School in Japan 1-1-1 Nomizu, Chofu City, 1-1-2 Tokyo 1-1-3 Tel: (0422) 34-5300 www.asij.ac.jp Map 2 BONUS 2: INTERNATIONAL SCHOOLS Aoba-Japan International School Hikarigaoka Campus 7-5-1 Hikarigaoka, Nerima-ku, Tokyo Tel: (03) 6904-3127 www.aobajapan.jp Map 3 TOKYO EXPAT JOB SEARCH GUIDE Aoba-Japan International School Shoto Campus 2-2-1 Shoto, Shibuya-ku, Tokyo Tel: (03) 5738-6556 www.aobajapan.jp Map 4 BONUS 2: INTERNATIONAL SCHOOLS British School in Tokyo 1-21-18 Shibuya, Shibuya-ku, Tokyo Tel: (03) 5467-4321 www.bst.ac.jp Map 5 TOKYO EXPAT JOB SEARCH GUIDE Canadian International School 5-8-20 Kita Shinagawa, Shinagawa-ku, Tokyo Tel: (03) 5793-3839 www.cisjapan.net Map 6 BONUS 2: INTERNATIONAL SCHOOLS Christian Academy in Japan 1-2-14 Shinkawacho, Higashi Kurume City, Tokyo Tel: (0424) 71-0022 www.caj.or.jp Map 7 TOKYO EXPAT JOB SEARCH GUIDE Columbia International School 153 Matsugo, Tokorozawa City, Saitama Tel: (04) 2946-1911 www.columbia-ca.co.jp Map 8 BONUS 2: INTERNATIONAL SCHOOLS Deutsche School Tokyo Yokohama 2-4-1 Chigasaki Minami, Tsuzuki-ku, Yokohama Tel: (045) 941-4841 www.dsty.jp Map 9 TOKYO EXPAT JOB SEARCH GUIDE Eton House International Pre-School Tokyo 9-2-16 Akasaka, Minato-ku, Tokyo Tel: (03) 6804-3322 www.etonhouse.co.jp Map 10 BONUS 2: INTERNATIONAL SCHOOLS Global Kids Academy -

University of Tokyo Yasuyuki Matsuda, Assoc
Introduction to the University of Tokyo Yasuyuki Matsuda, Assoc. Prof. (Deputy Director, International Admission Office, UTokyo) What is your dream university? University is where… you gain professional knowledge and skills you explore the academic world with leading researchers you make life-long friends you immerse in new social/cultural environment with safe and comfortable living environment affordable living expenses UTokyo can offer all of them! Introduction to the University of Tokyo (18th November 2014) UTokyo can be your dream university Why Japan? Why Tokyo? Why UTokyo? What PEAK can offer to you? Introduction to the University of Tokyo (18th November 2014) Introduction of the city of Tokyo Introduction to the University of Tokyo (18th November 2014) Tokyo is… one of the largest cities in the world, with diverse cultural activities. Name of the city Population (million) Tokyo* 37.83 Delhi 24.95 Shanghai 22.99 Mexico City 20.84 Sao Paulo 20.83 Mumbai 20.74 Osaka 20.12 Beijing 19.52 New York 18.59 Sources: the U.S. Census Bureau and Times Atlas of the World Introduction to the University of Tokyo (18th November 2014) Tokyo is… one of the global financial hubs as well. Name of the stock Market Capitalization exchange (USD bn) New York Stock Exchange 18,779 NASDAQ 6,683 Tokyo Stock Exchange 4,485 Euronext 3,504 London Stock Exchange 3,396 Hong Kong Stock Exchange 3,146 Shanghai Stock Exchange 2,869 Toronto Stock Exchange 2,204 Sources: the world federation of exchanges monthly report Sep. 2014 Introduction to the University -
Non-Existing Governmental Bodies)
存在しない日本政府機関 (Non-Existing Governmental Bodies) 電話番号又はファックス番号 商号、名称又は氏名等 所在地又は住所 ウェブサイトURL 掲載時期 (Phone Number and/or Fax (Name) (Location) (Website) (Publication) Number) Japanese Bureau of Mergers 31 floor, Midtown Tower, 9-7-1 2019年9月 Tel: +81 3 4572 0701 https://japbma.org/ and Acquisitions Akasaka, Minato, Tokyo, Japan (September 2019) Metropolitan Financial 8F Humax Ebisu Building, 2019年6月 Services & Futures Ebisu Minami 1-1-1, Shibuya-ku, Tel: +81 3 4579 5647 www.mfinsfa.com (June 2019) Authority Tokyo, ZIP 150-0022 STEP Roppongi Bldg. West 1F, Japanese Securities and 2019年6月 6-8-10 Roppongi, Minato-ku, Tel: +81 3 4510 7897 http://jaseca-gov.org Compliance Authority (June 2019) Tokyo, ZIP 106-0032 World Udagawa Bldg. 6F, 36-6, Foreign Securities 2019年6月 Udagawa-cho, Shibuya-ku, Tokyo, and Bond commission (June 2019) ZIP 150-0042 Foreign Securities 3-7-1 Kasumigaseki,Chiyodaku 2019年6月 Tel: +81 3 4520 8922 https://www.fssa-gov.org/ Supervisory Authority Tokyo, ZIP 100-0013 (June 2019) Axes 7th Building 6F, 3-17-4, 2019年6月 Equity Regulatory Authority Shibuya-ku, Tokyo, ZIP 150- Tel: +81 3 4520 8934 https://era-gov.org/ (June 2019) 0002 Mita Belljyu Building, Floor Tel: +81 3 4579 0731 24, 2018年11月 Tatler Cox Fax: +81 3 6800 2769 [email protected] 5-36-7 Shiba, Minato-ku, Tokyo (November 2018) Shiodome City Center 1-5-2, Foreign Securities Exchange Higashi - Shinbashi, Minato-ku, 2018年11月 Tel: +81 3 4510 7815 http://fsec-gov.org/ Commission Tokyo, (November 2018) ZIP 105-7140 29th floor, C tower, 3-7-1 Mergers and Consolidations Nishi -

Comforia Residential REIT, Inc 21-1 Dogenzaka 1-Chome, Shibuya-Ku,Tokyo Takehiro Izawa Executive Director (Code: 3282)
March 12, 2021 For Immediate Release Real Estate Investment Trust Securities Issuer: Comforia Residential REIT, Inc 21-1 Dogenzaka 1-chome, Shibuya-ku,Tokyo Takehiro Izawa Executive Director (Code: 3282) Asset Management Company: TLC REIT Management Inc. Hiroyuki Tohmata President & CEO Inquiries: Kentaro Yoshikawa General Manager of Strategy Department Comforia Management Division (TEL: +81-3-6455-3388) Notice Concerning Acquisition and Sale of Investment Assets Comforia Residential REIT, Inc (“CRR”) announces that TLC REIT Management Inc. (“TRM”), to which CRR entrusts management of its assets decided today for CRR to acquire the investment asset as shown below 1 (1), and sell the investment asset as shown below 1 (2). (hereafter referred to as the “Acquisition” and the “Sale” respectively and the “Transactions” collectively). 1. Summary of the Transactions (1) Summary of the Acquisition Acquisition Price No. Type of Asset Property Name (thousand yen) (Note1) Beneficial Interest in 1 COMFORIA OMIYA(Note2) 4,420,300 Real Estate Trust Total 4,420,300 (Note1) “Acquisition Price” denotes the amount exclusive of the various expenses required in the acquisition of the concerned asset, etc. (brokerage commission, taxes and public dues, etc.) (the amount of real estate or beneficial interest in real estate trust specified in the Agreement on Purchase and Sale). (Note2) Although the current property name is “SAION OMIYA”, CRR plans to change the name to “COMFORIA OMIYA” about one month after the acquisition. The current property name will be