DOCSLIB.ORG

Downloaded from the Online Library of the International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Downloaded from the Online Library of the International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE) INTERNATIONAL SOCIETY FOR SOIL MECHANICS AND GEOTECHNICAL ENGINEERING This paper was downloaded from the Online Library of the International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE). The library is available here: https://www.issmge.org/publications/online-library This is an open-access database that archives thousands of papers published under the Auspices of the ISSMGE and maintained by the Innovation and Development Committee of ISSMGE. 11/1 Stability of Natural Slopes in Quick Clays Stabilite des Pentes dans I'Argile Sensible G. AAS Civil Engineer, Norwegian G eotechnical Institute, O slo, Norway SYNOPSIS This paper attempts to explain the frequently occur ring flake- type quick clay landslides, characterize d by the ’arge volumes involved and by a sudden and very rapid fai lure along a nearly horizontal sliding surface. A conventiontional effective stress analysis based on a potential sliding surface and pore pressures p rior to failure is unable to express the risk of sliding. It seems pos sible, however, to determine a limit value of the s hear stress acting along such a sliding surface. This critical shear s tress implies that the clay will start yielding when subjected to any undrained load increment. Such critical shear stres s values have been determined by direct simple shea r tests, and are compared to the average shear stress along the slid ing surface calculated for a number of previous qui ck clay slides. INTRODUCTION vertical effective stress <Jn and a horizontal effective stress Ko*cr,j both principal stresses Statistically, at intervals of about four years, la rge quick clay slides involving clay masses of the orde r of millions of m^ occur in Norway. A nearly horizontal sli­ ding surface and a very gently inclined average slope are characteristic features of this type of earthslide. Ex­ Al ja\ perience (Aas, 1979) shows that the extent of the s lide area in the direction of sliding is of the order of 7- 15 t o times the corresponding difference in terrain level . t h t Quick clay slides frequently start without any warning and develop very rapidly embracing an area of sever al hundred thousands of m^ within a few minutes or les s. It seems to be a fact, however, that animals, like for inst­ ance horses, in some cases got nervous a few hours before the slide occurred. A possible explanation for this might be minor ground vibrations caused by stress redistr ibu­ tions in the quick clay. Quick clay slides seem to be, almost as a rule, initiated by a small increase in aver­ age shear stress caused by for instance intensive s tream Fig. 1. Stress conditions in clay element at potent i­ erosion, increased unit weight of top soil layer af ter al sliding surface before (A) and after (B) heavy rainfall, or earthworks for agricultural purp oses. applying a horizontal shear stress, The typical quick clay slide is frequently describe d in The applied horizontal force causes a shear stress Th the literature as a combination of a minor initial slide along the horizontal and vertical planes. When added to and a progressive failure process developing very r apidly the existing stresses, the applied stresses result in and spreading in all directions from the gate opened by both a change in magnitude and a rotation through an the first slide. As will be seen from examples pres ented angle v of the principal stresses. Denoting by tan ipm ob in this paper, another common failure mechanism imp lies a the maximum value of shear stress to effective normal clay volume sliding out as a huge flake. stress acting along the plane inclined ( 45*i/2ip'mob- v ) to the horizontal plane, and supposing that the str ess The paper attempts to explain these flake- type slid es change leads to an increase in pore pressure, Auw, one taking into account the quite peculiar strength proper­ may derive the following general expression for xH (Fig.l): ties of quick clays and the unique stress situation ex­ isting in the failure zone. x = cr ( D H o If one now assumes that t H is gradually increased under FAILURE MECHANISM IN QUICK CLAY fully drained conditions, yielding will take place along the critical plane when 'P'mob equals vp’ . The cor respon­ Fig. 1 shows a very idealized flake- type slide. A r igid ding stress conditions for the clay element are shown by block is displaced along a potential horizontal sli ding the circle of stress C in Fig. 2 a, and the value o f surface. Prior to being affected by the horizontal' force, xH,i»a 'S given by Eqn. 1 when inserting sinip'mob = a clay eTement on the failure surface was subjected to a sin tp' and Auw = 0. 333 11/1 of low sensitivity, lies in the different ways the two types of clay react to a sudden change in applied s tress. This is clearly demonstrated in Fig. 3 which gives data from undrained, active (compression) triaxial tests on specimens from 3 quick clay deposits and 2 clays of low sensitivity. All specimens were recondolidated to i n- situ stresses and then loaded to failure by increasing t he vertical stress. The lower diagram in Fig. 3 indicates that for all clays there exist a nearly unique relationship between changes in (a, - 03 )/( 0 | *Oj ) and subsequent changes in pore pressures uw as long as the shear stress/effective normal stress ratio does not exceed a certain value. If one assumes no cohesion intercept for these normally co nsoli­ dated clays, ( 0.-03 )/(aj'*Oj) equals sir"Pjnob and one Fig. 2. a) Stress conditions in clay element at gets from the diagram &uw/Oo'Asinvp1 - o.75 first yielding (C) and at drained failure along horizontal plane (D) At a certain value of sin*p' ob = sin, which varies b) Corresponding stress conditions if quick between 0.42 and 0.46 for tne three quick clays con sider clay ed, the rati0 Auw/cJ- Asinip1 suddenly increases drastically to values of 2.5 - 6 . The plastic clay of low sensitivi­ Due to the fact that sliding along the critical pla ne ty does not show any tendency for changing its rate of in the clay element, is not kinematically possible under pore pressure increase, while there is a very moder ate the rigid block (Fig. 1), yielding along this plane will increase in Auw/oj,- Asinip' for the lean clay of l ow sen­ not lead to a sliding failure. Thus, a further incr ease sitivity at about same value of 'P^ob as for t(le q uick in is possible because a simultaneously induced in­ clays. crease in horizontal stress provide for the stabili ty of the clay element. If one again assumes drained cond itions, The upper diagram in Fig. 3 shows how the maximum s hear the circle of stress moves outwards in Fig. 2 a, at all stress in the specimens, normalized with respect to tTg , times touching the failure envelope until the horizontal 1/2 (0 ,- o3 ) _/ Oo varies with sin'Pjncib . As a consequence plane becomes the critical sliding one. Then xH = CTo t an ' > of the regular increases in pore pressures, all cla ys be­ which may correspond to twice the value of xHat sta rt of have the same way for vP(|1ob<>Pcr corresponding to yielding. This value represents the maximum possibl e A [^- (o, - o3) ] / Og. Asinvp'~ 0.75 • For the quick clays,in shear resistance that can be mobilized along a hori zon­ contrast to the other ones, the dramatic increases in tal plane for a long term condition in normally con soli­ pore pressures thereafter, lead to a rapid decrease in dated clay. shear resistance in spite of the fact that mobilize d friction angle is continually increasing towards it s This paper attempts to illustrate that the correspo nding ultimate value corresponding to ( O,1 /a j ) max shear strength along a horizontal plane that governs the long term stability in quick clay, is considerably lower The most important information to be drawn from Fig . 3 than the theoretical value given above. This is par tly is that the values of Auw/Oq- Asinip1 at mobilizati on of due to the fact that yielding in quick clay starts at a Vtr in the quick clays, exceed by far the critical mobilized friction angle ip' lower than ip' . The main value figured out previously. Consequently, in- situ reason is, however, that ip'cr represents a critica l shear elements of these clays, carrying shear stresses co rre­ stress/effective normal stress ratio (Bjerrum and Kenney, sponding to vr>'ob = >p’Cr along any plane, will yi eld at 1968) at which a further sudden increase in shear s tress once if subjected to a sudden shear stress incremen t, is impossible as the increased value of 'P'mob''S more although 'Pjnot) is substantially less than ip' . than compensated for by the simultaneous decrease i n effective stresses due to rise in pore pressures. This is The stress- strain conditions in elements along a pl ane, visualized in Fig. 2 b, which shows that the circle of horizontal or gently inclined slip surface in- situ are stress moves towards the origin without Th being changed, best simulated in the laboratory by direct simple s hear until failure occurs along the horizontal plane when tests (Bjerrum and Landva, 1966). A specimen mounted in a confining membrane, is reconsolidated to in- situ (°o -A u w ) = TH f/fan«Pj stresses and then subjected to a gradually increasi ng The critical value of the ratio between increase in pore horizontal shear stress.
Load more

Recommended publications
  • Geotechnical and Geologic Constraints on Tsunamigenic Submarine Landslides
    GEOTECHNICAL AND GEOLOGIC CONSTRAINTS ON TSUNAMIGENIC SUBMARINE LANDSLIDES H.J. LEE U.S. Geological Survey, 345 Middlefield Road, Menlo Park, CA 94025 USA Abstract Modeling submarine-landslide-induced tsunamis requires many simplifications of the landslide process, although the real world is much more complicated. Clearly tsunami modelers cannot consider all facets, but there is value in being aware of the complications. This paper describes the many environments in which submarine landslides can occur and the triggers that typically initiate them. Earthquakes acting on continental or canyon slopes comprise probably the most common scenario but many other combinations of environments and triggers are possible. Surprisingly, many sediment-covered slopes in highly seismically active areas have not failed. A possible explanation for this phenomenon is a process called “seismic strengthening.” The existence of such a process reduces somewhat the risk of landslide tsunamis along active margins while maintaining the risk along passive margins. Once a trigger has initiated a landslide in one of the vulnerable environments, failed masses begin to move downslope. Depending upon initial density state, the masses may convert into fluid-like sediment flows or even more dilute turbidity currents. A model for quantifying the tendency to flow is provided. Finally, a case study of the landslides and landslide tsunamis that occurred in Port Valdez, Alaska, during the 1964 Great Alaska Earthquake is provided. The excellent data base, including before and after bathymetry, shows that both large rigid block motion and mobilized sediment flows can occur near each other during the same event. The intact blocks are more efficient in producing tsunamis but the sediment flow can move farther and can erode and entrain considerable bottom sediment as they progress across the seafloor.
    [Show full text]
  • Landslide Risks in the Göta River Valley in a Changing Climate
    Landslide risks in the Göta River valley in a changing climate Final report Part 2 - Mapping GÄU The Göta River investigation 2009 - 2011 Linköping 2012 The Göta River investigation Swedish Geotechnical Institute (SGI) Final report, Part 2 SE-581 93 Linköping, Sweden Order Information service, SGI Tel: +46 13 201804 Fax: +46 13 201914 E-mail: [email protected] Download the report on our website: www.swedgeo.se Photos on the cover © SGI Landslide risks in the Göta River valley in a changing climate Final report Part 2 - Mapping Linköping 2012 4 Landslide risks in the Göta älv valley in a changing climate 5 Preface In 2008, the Swedish Government commissioned the Swedish Geotechnical Institute (SGI) to con- duct a mapping of the risks for landslides along the entire river Göta älv (hereinafter called the Gö- ta River) - risks resulting from the increased flow in the river that would be brought about by cli- mate change (M2008/4694/A). The investigation has been conducted during the period 2009-2011. The date of the final report has, following a government decision (17/11/2011), been postponed until 30 March 2012. The assignment has involved a comprehensive risk analysis incorporating calculations of the prob- ability of landslides and evaluation of the consequences that could arise from such incidents. By identifying the various areas at risk, an assessment has been made of locations where geotechnical stabilising measures may be necessary. An overall cost assessment of the geotechnical aspects of the stabilising measures has been conducted in the areas with a high landslide risk.
    [Show full text]
  • Assessment of Liquefaction/Cyclic Failure Potential of Alluvial Deposits on the Eastern Coast of Cyprus
    Missouri University of Science and Technology Scholars' Mine International Conferences on Recent Advances 2010 - Fifth International Conference on Recent in Geotechnical Earthquake Engineering and Advances in Geotechnical Earthquake Soil Dynamics Engineering and Soil Dynamics 26 May 2010, 4:45 pm - 6:45 pm Assessment of Liquefaction/Cyclic Failure Potential of Alluvial Deposits on the Eastern Coast of Cyprus Huriye Bilsel Eastern Mediterranean University, Cyprus Goknur Erhan Eastern Mediterranean University, Cyprus Turan Durgunoglu Bogazici University, Turkey Follow this and additional works at: https://scholarsmine.mst.edu/icrageesd Part of the Geotechnical Engineering Commons Recommended Citation Bilsel, Huriye; Erhan, Goknur; and Durgunoglu, Turan, "Assessment of Liquefaction/Cyclic Failure Potential of Alluvial Deposits on the Eastern Coast of Cyprus" (2010). International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics. 3. https://scholarsmine.mst.edu/icrageesd/05icrageesd/session01/3 This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. This Article - Conference proceedings is brought to you for free and open access by Scholars' Mine. It has been accepted for inclusion in International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics by an authorized administrator of Scholars' Mine. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. ASSESSMENT OF LIQUEFACTION/CYCLIC FAILURE POTENTIAL OF ALLUVIAL DEPOSITS ON THE EASTERN COAST OF CYPRUS Huriye Bilsel Goknur Erhan Turan Durgunoglu Eastern Mediterranean University Eastern Mediterranean University P.E., Ph.D., F. ASCE Famagusta- N.
    [Show full text]
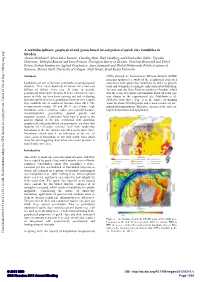
  • A Multidisciplinary Geophysical and Geotechnical Investigation of Quick
    A multidisciplinary geophysical and geotechnical investigation of quick clay landslides in Sweden Alireza Malehmir*, Silvia Salas Romero, Chunling Shan, Emil Lundberg and Christopher Juhlin, Uppsala University; Mehrdad Bastani and Lena Persson, Geological Survey of Sweden; Charlotte Krawczyk and Ulrich Polom, Leibniz Institute for Applied Geophysics; Anna Adamczyk and Michal Malinowski, Polish Academy of Sciences; Marcus Gurk, University of Cologne; Nazli Ismail, Syiah Kuala University Summary (SEG) through its Geoscientists Without Borders (GWB) program sponsored a study of the geophysical properties Landslides are one of the most commonly occurring natural associated with quick-clay landslides in order to provide disasters. They claim hundreds of human lives and cost tools and techniques to mitigate risks associated with them. billions of dollars every year. In order to provide An area near the Göta River in southwest Sweden, which geophysical tools and techniques to better characterize sites was the scene of a quick clay landslide about 40 years ago, prone to slide, we have been carrying out and evaluating was chosen as the experimental site (Malehmir et al., potential utility of several geophysical surveys over a quick 2013a,b). Göta River (Fig. 1) is the source of drinking clay landslide site in southwest Sweden since 2011. The water for about 700,000 people and is used extensively for measurements include 2D and 3D P- and S-wave high industrial transportation. Therefore, areas near the river are resolution surface seismics, radio- and controlled-source highly industrialized and populated. electromagnetics, geoelectrics, ground gravity and magnetic surveys. A particular focus here is given to the seismic studies in the site.
    [Show full text]
  • Appendix A. Basic Information About Landslides 60 the Landslide Handbook—A­ Guide to Understanding Landslides
    Appendix A. Basic Information about Landslides 60 The Landslide Handbook —A Guide to Understanding Landslides Part 1. Glossary of Landslide Terms Full references citations for glossary are at the end of the list. alluvial fan An outspread, gently sloping Digital Terrain Model (DTM) The term used Geographic Information System (GIS) A mass of alluvium deposited by a stream, by United States Department of Defense and computer program and associated data bases especially in an arid or semiarid region other organizations to describe digital eleva- that permit cartographic information (includ- where a stream issues from a narrow canyon tion data. (Reference 3) ing geologic information) to be queried onto a plain or valley floor. Viewed from drawdown Lowering of water levels in riv- by the geographic coordinates of features. above, it has the shape of an open fan, the ers, lakes, wells, or underground aquifers due Usually the data are organized in “layers” apex being at the valley mouth. (Reference 3) to withdrawal of water. Drawdown may leave representing different geographic entities such as hydrology, culture, topography, and bedding surface/plane In sedimentary or unsupported banks or poorly packed earth so forth. A geographic information system, stratified rocks, the division planes that sepa- that can cause landslides. (Reference 3) or GIS, permits information from different rate each successive layer or bed from the electronic distance meter (EDM) A device layers to be easily integrated and analyzed. one above or below. It is commonly marked that emits ultrasonic waves that bounce off (Reference 3) by a visible change in lithology or color.
    [Show full text]
  • 4.5.1 Mapping of Quick Clay Zones ...43
    No. 1 BI Norwegian Business School - campus Oslo GRA 19703 Master Thesis Thesis Master of Science Investigating key drivers of institutional change in natural hazards fields: An empirical study of quick clay management in Norway ID number: 1023050, 1023092 Start: 15.01.2020 09.00 Finish: 01.09.2020 12.00 No. 1 GRA 19703 1023050 1023092 ID number: 1023050 ID number: 1023092 Investigating key drivers of institutional change in natural hazards fields: An empirical study of quick clay management in Norway Hand-in date: 22.07.2020 Campus: BI Oslo Study program: MSc in Business - Major in Strategy Supervisor: Lena Elisabeth Bygballe No. 1 GRA 19703 1023050 1023092 Table of contents TABLE OF CONTENTS................................................................................................................. I LIST OF FIGURES AND TABLES ............................................................................................ III ACKNOWLEDGEMENT ............................................................................................................ IV ABSTRACT .................................................................................................................................... V 1 INTRODUCTION ................................................................................................................. 1 2 LITERATURE REVIEW ..................................................................................................... 3 2.1 INSTITUTIONAL CHANGE ........................................................................................................
    [Show full text]
  • The Turnagain Heights Landslide in Anchorage, Alaska
    SOIL MECHANICS AND BITUMINOUS MATERIALS RESEARCH LABORATORY THE TURNAGAIN HEIGHTS LANDSLIDE IN ANCHORAGE, ALASKA by H. BOLTON SEED and STANLEY D. WILSON DEPARTMENT OF CIVIL ENGINEERING INSTITUTE OF TRANSPORTATION AND TRAFFIC ENGINEERING University of California · Berkeley THE TURNAGAIN,HEIGHTS LANDSLIDE IN ANCHORAGE, ALASKA by 1 H. Bolton Seed and Stanley D. Wilson2 1. Professor of Civil Engineering, University of California, Berkeley. 2. Vice-President, Shannon & Wilson, Inc., Seattle, Washington. The Turnagain Heights Landslide in Anchorage, Alaska by H. Bolton Seed and Stanley D. Wilson Description of the Slide During the Alaskan earthquake of March 27, 1964 ~number of major 1 2 slides occurred in the City of Anchorage. • The largest of these slides I was.that along the coastline in the Turnagain Heights area. An aerial view of the slide is shown in Fig. la and a plan of the slide area in Fig. 3. The coast line in this area was marked by bluffs some 70 feet high, sloping at about 1-1/2:1 down to the bay. The slide extended about 8500 feet from west to east along the bluff-line and retrogressed inward from the coast a distance of about 1200 feet at the west end and about 600 feet at the east end. The total area within the slide zone was thus about 130 acres. Within the slide area the original ground surface was completely devastated by displacements which broke up the ground into a complex system of ridges and depressions, producing an extremely irregular and hummocky surface. A general view of the central part of the slide area is shown in Fig.
    [Show full text]
  • Downloaded from the Online Library of the International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE)
    INTERNATIONAL SOCIETY FOR SOIL MECHANICS AND GEOTECHNICAL ENGINEERING This paper was downloaded from the Online Library of the International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE). The library is available here: https://www.issmge.org/publications/online-library This is an open-access database that archives thousands of papers published under the Auspices of the ISSMGE and maintained by the Innovation and Development Committee of ISSMGE. A FIELD STUDY OF FACTORS RESPONSIBLE FOR QUICK CLAY SLIDES. ETUDE SUR PLACE DES FACTEURS RESPON SABLES DES GLISSEM ENTS EN ARGILES TRES SENSITIVES L. BJERRUM , T: LOKEN , S. HEIBERG, R. FOSTER. Norwegian Geotechnical Institute, Oslo, Norway. The City University, London, U. K. SYNOPSIS The paper describes the result of a field study of a 45 km^ large m arine clay area 40 km nort h­ east of Oslo. The scope of the study was to isolate , describe, and evaluate the relative im portance of the various factors and processes responsible for the o ccurrence of quick clay slides. The m ost important finding of the study is probably the establishm ent of a zone of aggression within which the risk of qu ick clay slides is greatest. It is concluded that the possib ility of preventing quick clay slides m ay exist by the con­ struction of thresholds in the stream s to reduce fu rther erosion. INTRODUCTION Within N orw ay's 40000 km^ of m arine clay area, HAUFRSFTFR KLÛFTA quick clay slides present a serious problem , each 220 century leading to loss of lives and property. In the study of this problem the Norwegian G eotechni­ cal Institute has hitherto concentrated its activit y * 180 6 on detailed investigations of individual slides.
    [Show full text]
  • Nicolet Landslide of November 1955, Quebec, Canada Crawford, C
    NRC Publications Archive Archives des publications du CNRC Nicolet landslide of November 1955, Quebec, Canada Crawford, C. B.; Eden, W. J. This publication could be one of several versions: author’s original, accepted manuscript or the publisher’s version. / La version de cette publication peut être l’une des suivantes : la version prépublication de l’auteur, la version acceptée du manuscrit ou la version de l’éditeur. For the publisher’s version, please access the DOI link below./ Pour consulter la version de l’éditeur, utilisez le lien DOI ci-dessous. Publisher’s version / Version de l'éditeur: https://doi.org/10.1130/Eng-Case-4.45 Engineering Geology Case Histories, 4, pp. 45-50, 1964-05-01 NRC Publications Record / Notice d'Archives des publications de CNRC: https://nrc-publications.canada.ca/eng/view/object/?id=cdd30548-d3a1-4452-98b8-49811be88d4f https://publications-cnrc.canada.ca/fra/voir/objet/?id=cdd30548-d3a1-4452-98b8-49811be88d4f Access and use of this website and the material on it are subject to the Terms and Conditions set forth at https://nrc-publications.canada.ca/eng/copyright READ THESE TERMS AND CONDITIONS CAREFULLY BEFORE USING THIS WEBSITE. L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site https://publications-cnrc.canada.ca/fra/droits LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB. Questions? Contact the NRC Publications Archive team at [email protected]. If you wish to email the authors directly, please see the first page of the publication for their contact information.
    [Show full text]
  • Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope
    geosciences Review Overview of Retrogressive Landslide Risk Analysis in Sensitive Clay Slope Blanche Richer * , Ali Saeidi , Maxime Boivin and Alain Rouleau Department of Applied Sciences, University of Quebec at Chicoutimi, Chicoutimi, QC G7H 2B1, Canada; [email protected] (A.S.); [email protected] (M.B.); [email protected] (A.R.) * Correspondence: [email protected] Received: 2 June 2020; Accepted: 18 July 2020; Published: 22 July 2020 Abstract: Sensitive clays are known for producing retrogressive landslides, also called spread or flowslides. The key characteristics associated with the occurrence of these landslides on a sensitive clay slope must be assessed, and the potential retrogressive distance must be evaluated. Common risk analysis methods include empirical methods for estimating the distance of potential retrogression, analytical limit equilibrium methods, numerical modelling methods using the strength reduction technique, and the integration of a progressive failure mechanism into numerical methods. Methods developed for zoning purposes in Norway and Quebec provide conservative results in most cases, even if they don’t cover the worst cases scenario. A flowslide can be partially analysed using analytical limit equilibrium methods and numerical methods having strength reduction factor tools. Numerical modelling of progressive failure mechanisms using numerical methods can define the critical parameters of spread-type landslides, such as critical unloading and the retrogression distance of the failure. Continuous improvements to the large-deformation numerical modeling approach allow its application to all types of sensitive clay landslides. Keywords: sensitive clay; quick clay; landslide; stability analysis; failure type; retrogressive distance 1. Introduction Clays are constituted of fine-grained soil material having a grain size of less than approximately 0.05 mm.
    [Show full text]
  • GIS-Based Modeling of Snowmelt-Induced Landslide Susceptibility of Sensitive Marine Clays Mohammad Al-Umar1, Mamadou Fall1* and Bahram Daneshfar2
    Al-Umar et al. Geoenvironmental Disasters (2020) 7:9 Geoenvironmental Disasters https://doi.org/10.1186/s40677-020-0142-8 RESEARCH Open Access GIS-based modeling of snowmelt-induced landslide susceptibility of sensitive marine clays Mohammad Al-Umar1, Mamadou Fall1* and Bahram Daneshfar2 Abstract In this study, a simulation tool, based on the combination of Geographic Information System (GIS) and Grid-Based Regional Slope-Stability Model (TRIGRS), is developed to assess and predict the snowmelt-induced landslides in areas of sensitive marine clays in the Ottawa region (Canada). Topographic, geologic, hydrologic, and geotechnical information of the study area, in addition to snowmelt intensity data for different periods, was required to conduct this modeling study. Snowmelt intensity records for periods of 6–48 h, 3–15 days, 25 days, and 30 days, as well as the information on historical landslides in the study area, were used to examine both the timing and location of shallow landslides due to snowmelt across the Ottawa region. The developed tool is validated by comparing the predicted landslide-susceptible areas with the historical landslide maps in the study area. A good agreement between the predicted and recorded historical landslides was obtained, which suggests that the developed GIS- TRIGRS based tool can predict relatively well the snowmelt-induced landslide susceptibility in the sensitive marine clays. The modeling results show that high slope areas of sensitive marine clays are more prone to snowmelt- induced landslides. As a result, this simulation tool could be used to assess and/or predict snowmelt-induced landslides in different areas of the Ottawa region, which is an important means for decision-making processes with respect to protecting the population and infrastructure against snow-melt induced marine clay landslides.
    [Show full text]
  • Description of the Landslide That Occurred at Lemieux on June 20
    1 National Research Conseil national Council Canada de recherches Canada ■ MC CARC Reprinted from Reimpression de la Canadian Revue Geotechnical canadienne Journal de geotechnique An earthflow in sensitive - Champlain Sea sediments at Lemieux, Ontario, June 20, 1993, and its impact on the South Nation River S.G. EVANS AND G.R. BROOKS Volume 31 • Number 3 • 1994 Pages 384— 394 CanadiS 384 An earthflow in sensitive Champlain Sea sediments at Lemieux, Ontario, s June 20, 1993, and its impact on the South Nation River S.G. EVANS AND G.R. BROOKS Geological Survey of Canada, 601 Booth Street, Ottawa, ON KIA 0E8, Canada Received September 16, 1993 Accepted January 27, 1994 A large (est. volume 2.8 X 10 6 m 3) landslide occurred in sensitive Leda clay on the east bank of the South Nation River at Lemieux, Ontario (45.4°N, 75.06°W), on June 20, 1993. The earthflow involved an area of about 17 ha and retrogressed a total of 680 m, 555 m into the flat plain above the river. No lives were lost but a motorist was injured when he drove into the landslide crater. The 1993 landslide occurred 4.5 km downstream of the well-known 1971 South Nation River landslide along a stretch of river that had experienced other historical landslides in 1895 and 1910. A band of earlier, undated, retrogressive sliding, between 100-130 m in width, was present at the base of the slope that failed in 1993, and the earthflow was probably triggered by a reactivation of these failures.
    [Show full text]