DOCSLIB.ORG

Binomial Random Walk

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Binomial Random Walk INTRODUCTION TO STOCHASTIC CALCULUS Borun D Chowdhury Stochastic Processes What is a stochastic process? Series of events where a variable takes random values X0, X1….. Xt … Causality requires Xt depends only on Xt’ where t’<t A Markovian process is a memory less stochastic process so that Xt depends only on Xt’ Often it is useful to look at the difference process Yt = Xt - Xt-1 Binomial Random Walk The workhorse of stochastic processes is the Binomial Random walk To understand that we first look at a Bernoulli process B(p), a random variable that is 1 with probability p and 0 with probability q E[B(p)] = p, V ar[B(p)] = p(1 p) − We then define a variable that takes values 1 with probability p and -1 with probability q X =2B(p) 1 i − and we have E[X ]=2p 1,Var[B(p)] = 4p(1 p) i − − This is a model for a step taken by a drunk Binomial Random Walk If the drunk takes n steps then we have a new random variable n Yn = Xi i Its expectation value is X E[Y ]= E[X ]=n(2p 1) n i − Its variance is X Var(Yn)= Var(Xi)+ Cov(Xi,Xj) i i=j X X6 If the different steps are not correlated (or better yet independent) Var(Y )=4np(1 p) n − Note Yn is also a stochastic process StochasticProcesses/RandomWalkAndWeinerProcess.ipynb at master · borundev/StochasticProcesses 02/06/16 14:19 self.p=p self.dt=dt self.nsteps=int(self.T/self.dt) Paths.__setup__(self) self.randoms=2*(np.random.binomial(1,self.p,self.npaths*(self.nsteps-1))-.5) self.randoms.shape=[self.npaths,self.nsteps-1] for i in range(self.nsteps-1): self.paths[:,i+1]=self.paths[:,i]+self.randoms[:,i] b_paths=BinaryPaths(11,1,6).get_paths() number_columns=2 number_rows=3 figsize(12, 9) for i,j in enumerate([(i/number_columns,i%number_columns) for i in range(number_columns*number_row s)]): plt.subplot2grid((number_rows,number_columns),j) plt.plot(b_paths[i],"--o") plt.xlabel("time") Binomial pltRandom.ylabel("position") Walk plt.ylim(-7,7) From Binomial Walk to Weiner Process but not back! Note that after n steps the scale of fluctuations around the mean The process described above is a Binomial process and happens in discrete times. However for analytical reasons we would like to take a continuum limit of the same. Although having done that, for computational reasons the latter is approximated by a discrete process again. The reason for the analytical expression in continuous time is actually tied to the central limit theorem which for our purposes states that the sum of many independent incrememts by random variables with well defined meanp and variance tends to a Gaussian process (the Gaussian is stable under such sums or, as they are known technically, convolutions).σn Thus if we cann pass to a domain where such convergence has happened we do not care about the microscopic model anymore. ⇠ If the above is not clear already, I hope the plots below will help. Here I generate random walks, same as before, for the time interval t = [0, 10) by deviding the interval in 10000 steps. Then we zoom into the central region (any region would do) by factors of 2. You will notice that for the first 5 zoom ins the path looks the same. However, after that the discrete nature of Bernoulli jumps start becoming visible. In [2]: T=10.0 num_steps_bernoulli=2**12 delta_t_bernoulli=T/num_steps_bernoulli https://github.com/borundev/StochasticProcesses/blob/master/RandomWalkAndWeinerProcess.ipynb Page 2 of 6 StochasticProcesses/RandomWalkAndWeinerProcess.ipynb at master · borundev/StochasticProcesses 02/06/16 14:19 self.p=p self.dt=dt self.nsteps=int(self.T/self.dt) Paths.__setup__(self) self.randoms=2*(np.random.binomial(1,self.p,self.npaths*(self.nsteps-1))-.5) self.randoms.shape=[self.npaths,self.nsteps-1] for i in range(self.nsteps-1): self.paths[:,i+1]=self.paths[:,i]+self.randoms[:,i] b_paths=BinaryPaths(11,1,6).get_paths() number_columns=2 number_rows=3 figsize(12, 9) for i,j in enumerate([(i/number_columns,i%number_columns) for i in range(number_columns*number_row s)]): plt.subplot2grid((number_rows,number_columns),j) plt.plot(b_paths[i],"--o") plt.xlabel("time") Binomial Random Walk plt.ylabel("position") plt.ylim(-7,7) Covariance of random walk Covariance of steps Cov(X ,X )=4p(1 p)δ n m − n,m From Binomial Walk to Weiner Process but not back! The process described above is a Binomial process and happens in discrete times. However for analytical reasons we would like to take a Covariance of paths continuum limit of the same. Although having done that, for computational reasons the latter is approximated by a discrete process again. The reason for the analytical expression in continuous time is actually tied to the central limit theorem which for our purposes states that the sum of many independent incrememts by random variables with well defined mean and variance tends to a Gaussian process (the Gaussian is stable under such sums or, as they are known technically, convolutions). Thus if we can pass to a domain where such convergence has happened we do not care about the microscopic model anymore. If the above is not clear already, I hope the plots below will help. Here I generate random walks, same as before, for the time interval t = [0, 10) Cov(Yn,Ym)=4min(n, m)p(1by deviding the interval pin 10000) steps. Then we zoom into the central region (any region would do) by factors of 2. You will notice that for the first 5 zoom ins the− path looks the same. However, after that the discrete nature of Bernoulli jumps start becoming visible. In [2]: T=10.0 num_steps_bernoulli=2**12 delta_t_bernoulli=T/num_steps_bernoulli https://github.com/borundev/StochasticProcesses/blob/master/RandomWalkAndWeinerProcess.ipynb Page 2 of 6 StochasticProcesses/RandomWalkAndWeinerProcess.ipynb at master · borundev/StochasticProcesses 02/06/16 14:19 b=BinaryPaths(10,delta_t_bernoulli,1) time_line=b.get_timeline() path=b[0] number_columns=2 number_rows=4 figsize(12, 9) StochasticProcesses/RandomWalkAndWeinerProcess.ipynb at master · borundev/StochasticProcesses# plot the entire path first and then regions zoomed02/06/16 in by 14factor:19 of 2s for i,j in enumerate([(i/number_columns,i%number_columns) for i in range(number_columns*number_row s)]): plt.subplot2grid((number_rows,number_columns),j) b=BinaryPaths(10,delta_t_bernoulli,1) time_line_for_plot=time_line[num_steps_bernoulli/2 -num_steps_bernoulli/(2**(i+1)):num_steps_b time_line=b.get_timeline() ernoulli/2 +num_steps_bernoulli/(2**(i+1))] path=b[0] path_for_plot=path[num_steps_bernoulli/2 -num_steps_bernoulli/(2**(i+1)):num_steps_bernoulli/2 +num_steps_bernoulli/(2**(i+1))] number_columns=2 number_rows=4 plt.plot(time_line_for_plot,path_for_plot) figsize(12, 9) plt.xlabel("time") A glimpse of the central limit theorem plt.ylabel("position") # plot the entire path first and then regions zoomed in by factor of 2s for i,j in enumerate([(i/number_columns,i%number_columns) for i in range(number_columns*number_row s)]): For a very plt.subplot2grid large number((number_rows of steps,number_columns),j) time_line_for_plot=time_line[num_steps_bernoulli/2 -num_steps_bernoulli/(2**(i+1)):num_steps_b ernoulli/2 +num_steps_bernoulli/(2**(i+1))] path_for_plot=path[num_steps_bernoulli/2 -num_steps_bernoulli/(2**(i+1)):num_steps_bernoulli/2 +num_steps_bernoulli/(2**(i+1))] plt.plot(time_line_for_plot,path_for_plot) plt.xlabel("time") plt.ylabel("position") Take the central half and zoom in The distribution looks the same (after rescaling) It is intructive to understand what is happening here clearly. The discussion below works for all values of p away from 0 and 1 for sufficiently large n. The change in position after n steps is given by Yn = 2Binomial(n, p) − n . For large enough n (depending on how important tail events are the cutoffs are different) this can be approximated by Yn ∼ 2(np, √‾n‾p‾(‾1‾‾−‾‾p‾)) − n = n(2p − 1) + 2√‾n‾p‾(‾1‾‾−‾‾p‾)(0, 1) = n(2p − 1) + √4‾‾n‾p‾(‾1‾‾−‾‾p‾)(0, 1) Specializing to p = .5, if we progressively look at an interval n we can approximate 2k It is intructive to understand what is happening here clearly. The discussion below works for all values of p away from and for sufficiently‾‾n‾ large 0 1Yn ∼ (0, 1) . k n √ 2 and the plot is qualitatively the same as long as k is not large enough to violate the Binomial to Gaussian approximation. In the plots above we The change in position after n steps is given by have the size of intervals Yn = 2Binomial(n, p) − n . For large enough n (depending on how important tail events are theIn cuto [7]:ffs areprint different) [num_steps_bernoulli this can be approximated/2** byk for k in range(9)] Yn ∼ 2(np, √‾n‾p‾[4096,(‾1‾‾−‾‾p‾) )2048,− n 1024, 512, 256, 128, 64, 32, 16] = n(2p − 1) + 2√‾n‾p‾(‾1‾‾−‾‾p‾)(0, 1) = n(2p − 1) + 4‾‾n‾p‾(‾1‾‾−‾‾p‾)(0, 1) https://github.com/borundev/StochasticProcesses/blob/master/RandomWalkAndWeinerProcess.ipynb√ Page 3 of 6 Specializing to p = .5, if we progressively look at an interval n we can approximate 2k ‾‾n‾ Yn ∼ (0, 1) √ 2k and the plot is qualitatively the same as long as k is not large enough to violate the Binomial to Gaussian approximation. In the plots above we have the size of intervals In [7]: print [num_steps_bernoulli/2**k for k in range(9)] [4096, 2048, 1024, 512, 256, 128, 64, 32, 16] https://github.com/borundev/StochasticProcesses/blob/master/RandomWalkAndWeinerProcess.ipynb Page 3 of 6 StochasticProcesses/RandomWalkAndWeinerProcess.ipynb at master · borundev/StochasticProcesses 02/06/16 14:19 b=BinaryPaths(10,delta_t_bernoulli,1) time_line=b.get_timeline() path=b[0] number_columns=2 number_rows=4 figsize(12, 9) # plot the entire path first and then regions zoomed in by factor of 2s for i,j in enumerate([(i/number_columns,i%number_columns) for i in range(number_columns*number_row s)]): plt.subplot2grid((number_rows,number_columns),j) time_line_for_plot=time_line[num_steps_bernoulli/2 -num_steps_bernoulli/(2**(i+1)):num_steps_b ernoulli/2 +num_steps_bernoulli/(2**(i+1))] path_for_plot=path[num_steps_bernoulli/2 -num_steps_bernoulli/(2**(i+1)):num_steps_bernoulli/2 +num_steps_bernoulli/(2**(i+1))] plt.plot(time_line_for_plot,path_for_plot) A glimpse pltof.xlabel the("time" central) limit theorem plt.ylabel("position") It is intructive to understand what is happening here clearly.
Load more

Recommended publications
  • Superprocesses and Mckean-Vlasov Equations with Creation of Mass
    Sup erpro cesses and McKean-Vlasov equations with creation of mass L. Overb eck Department of Statistics, University of California, Berkeley, 367, Evans Hall Berkeley, CA 94720, y U.S.A. Abstract Weak solutions of McKean-Vlasov equations with creation of mass are given in terms of sup erpro cesses. The solutions can b e approxi- mated by a sequence of non-interacting sup erpro cesses or by the mean- eld of multityp e sup erpro cesses with mean- eld interaction. The lat- ter approximation is asso ciated with a propagation of chaos statement for weakly interacting multityp e sup erpro cesses. Running title: Sup erpro cesses and McKean-Vlasov equations . 1 Intro duction Sup erpro cesses are useful in solving nonlinear partial di erential equation of 1+ the typ e f = f , 2 0; 1], cf. [Dy]. Wenowchange the p oint of view and showhowtheyprovide sto chastic solutions of nonlinear partial di erential Supp orted byanFellowship of the Deutsche Forschungsgemeinschaft. y On leave from the Universitat Bonn, Institut fur Angewandte Mathematik, Wegelerstr. 6, 53115 Bonn, Germany. 1 equation of McKean-Vlasovtyp e, i.e. wewant to nd weak solutions of d d 2 X X @ @ @ + d x; + bx; : 1.1 = a x; t i t t t t t ij t @t @x @x @x i j i i=1 i;j =1 d Aweak solution = 2 C [0;T];MIR satis es s Z 2 t X X @ @ a f = f + f + d f + b f ds: s ij s t 0 i s s @x @x @x 0 i j i Equation 1.1 generalizes McKean-Vlasov equations of twodi erenttyp es.
    [Show full text]
  • Partnership As Experimentation: Business Organization and Survival in Egypt, 1910–1949
    Yale University EliScholar – A Digital Platform for Scholarly Publishing at Yale Discussion Papers Economic Growth Center 5-1-2017 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç Timothy Guinnane Follow this and additional works at: https://elischolar.library.yale.edu/egcenter-discussion-paper-series Recommended Citation Artunç, Cihan and Guinnane, Timothy, "Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949" (2017). Discussion Papers. 1065. https://elischolar.library.yale.edu/egcenter-discussion-paper-series/1065 This Discussion Paper is brought to you for free and open access by the Economic Growth Center at EliScholar – A Digital Platform for Scholarly Publishing at Yale. It has been accepted for inclusion in Discussion Papers by an authorized administrator of EliScholar – A Digital Platform for Scholarly Publishing at Yale. For more information, please contact [email protected]. ECONOMIC GROWTH CENTER YALE UNIVERSITY P.O. Box 208269 New Haven, CT 06520-8269 http://www.econ.yale.edu/~egcenter Economic Growth Center Discussion Paper No. 1057 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç University of Arizona Timothy W. Guinnane Yale University Notes: Center discussion papers are preliminary materials circulated to stimulate discussion and critical comments. This paper can be downloaded without charge from the Social Science Research Network Electronic Paper Collection: https://ssrn.com/abstract=2973315 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç⇤ Timothy W. Guinnane† This Draft: May 2017 Abstract The relationship between legal forms of firm organization and economic develop- ment remains poorly understood. Recent research disputes the view that the joint-stock corporation played a crucial role in historical economic development, but retains the view that the costless firm dissolution implicit in non-corporate forms is detrimental to investment.
    [Show full text]
  • A Model of Gene Expression Based on Random Dynamical Systems Reveals Modularity Properties of Gene Regulatory Networks†
    A Model of Gene Expression Based on Random Dynamical Systems Reveals Modularity Properties of Gene Regulatory Networks† Fernando Antoneli1,4,*, Renata C. Ferreira3, Marcelo R. S. Briones2,4 1 Departmento de Informática em Saúde, Escola Paulista de Medicina (EPM), Universidade Federal de São Paulo (UNIFESP), SP, Brasil 2 Departmento de Microbiologia, Imunologia e Parasitologia, Escola Paulista de Medicina (EPM), Universidade Federal de São Paulo (UNIFESP), SP, Brasil 3 College of Medicine, Pennsylvania State University (Hershey), PA, USA 4 Laboratório de Genômica Evolutiva e Biocomplexidade, EPM, UNIFESP, Ed. Pesquisas II, Rua Pedro de Toledo 669, CEP 04039-032, São Paulo, Brasil Abstract. Here we propose a new approach to modeling gene expression based on the theory of random dynamical systems (RDS) that provides a general coupling prescription between the nodes of any given regulatory network given the dynamics of each node is modeled by a RDS. The main virtues of this approach are the following: (i) it provides a natural way to obtain arbitrarily large networks by coupling together simple basic pieces, thus revealing the modularity of regulatory networks; (ii) the assumptions about the stochastic processes used in the modeling are fairly general, in the sense that the only requirement is stationarity; (iii) there is a well developed mathematical theory, which is a blend of smooth dynamical systems theory, ergodic theory and stochastic analysis that allows one to extract relevant dynamical and statistical information without solving
    [Show full text]
  • POISSON PROCESSES 1.1. the Rutherford-Chadwick-Ellis
    POISSON PROCESSES 1. THE LAW OF SMALL NUMBERS 1.1. The Rutherford-Chadwick-Ellis Experiment. About 90 years ago Ernest Rutherford and his collaborators at the Cavendish Laboratory in Cambridge conducted a series of pathbreaking experiments on radioactive decay. In one of these, a radioactive substance was observed in N = 2608 time intervals of 7.5 seconds each, and the number of decay particles reaching a counter during each period was recorded. The table below shows the number Nk of these time periods in which exactly k decays were observed for k = 0,1,2,...,9. Also shown is N pk where k pk = (3.87) exp 3.87 =k! {− g The parameter value 3.87 was chosen because it is the mean number of decays/period for Rutherford’s data. k Nk N pk k Nk N pk 0 57 54.4 6 273 253.8 1 203 210.5 7 139 140.3 2 383 407.4 8 45 67.9 3 525 525.5 9 27 29.2 4 532 508.4 10 16 17.1 5 408 393.5 ≥ This is typical of what happens in many situations where counts of occurences of some sort are recorded: the Poisson distribution often provides an accurate – sometimes remarkably ac- curate – fit. Why? 1.2. Poisson Approximation to the Binomial Distribution. The ubiquity of the Poisson distri- bution in nature stems in large part from its connection to the Binomial and Hypergeometric distributions. The Binomial-(N ,p) distribution is the distribution of the number of successes in N independent Bernoulli trials, each with success probability p.
    [Show full text]
  • Lecture 19: Polymer Models: Persistence and Self-Avoidance
    Lecture 19: Polymer Models: Persistence and Self-Avoidance Scribe: Allison Ferguson (and Martin Z. Bazant) Martin Fisher School of Physics, Brandeis University April 14, 2005 Polymers are high molecular weight molecules formed by combining a large number of smaller molecules (monomers) in a regular pattern. Polymers in solution (i.e. uncrystallized) can be characterized as long flexible chains, and thus may be well described by random walk models of various complexity. 1 Simple Random Walk (IID Steps) Consider a Rayleigh random walk (i.e. a fixed step size a with a random angle θ). Recall (from Lecture 1) that the probability distribution function (PDF) of finding the walker at position R~ after N steps is given by −3R2 2 ~ e 2a N PN (R) ∼ d (1) (2πa2N/d) 2 Define RN = |R~| as the end-to-end distance of the polymer. Then from previous results we q √ 2 2 ¯ 2 know hRN i = Na and RN = hRN i = a N. We can define an additional quantity, the radius of gyration GN as the radius from the centre of mass (assuming the polymer has an approximately 1 2 spherical shape ). Hughes [1] gives an expression for this quantity in terms of hRN i as follows: 1 1 hG2 i = 1 − hR2 i (2) N 6 N 2 N As an example of the type of prediction which can be made using this type of simple model, consider the following experiment: Pull on both ends of a polymer and measure the force f required to stretch it out2. Note that the force will be given by f = −(∂F/∂R) where F = U − TS is the Helmholtz free energy (T is the temperature, U is the internal energy, and S is the entropy).
    [Show full text]
  • 8 Convergence of Loop-Erased Random Walk to SLE2 8.1 Comments on the Paper
    8 Convergence of loop-erased random walk to SLE2 8.1 Comments on the paper The proof that the loop-erased random walk converges to SLE2 is in the paper \Con- formal invariance of planar loop-erased random walks and uniform spanning trees" by Lawler, Schramm and Werner. (arxiv.org: math.PR/0112234). This section contains some comments to give you some hope of being able to actually make sense of this paper. In the first sections of the paper, δ is used to denote the lattice spacing. The main theorem is that as δ 0, the loop erased random walk converges to SLE2. HOWEVER, beginning in section !2.2 the lattice spacing is 1, and in section 3.2 the notation δ reappears but means something completely different. (δ also appears in the proof of lemma 2.1 in section 2.1, but its meaning here is restricted to this proof. The δ in this proof has nothing to do with any δ's outside the proof.) After the statement of the main theorem, there is no mention of the lattice spacing going to zero. This is hidden in conditions on the \inner radius." For a domain D containing 0 the inner radius is rad0(D) = inf z : z = D (364) fj j 2 g Now fix a domain D containing the origin. Let be the conformal map of D onto U. We want to show that the image under of a LERW on a lattice with spacing δ converges to SLE2 in the unit disc. In the paper they do this in a slightly different way.
    [Show full text]
  • Contents-Preface
    Stochastic Processes From Applications to Theory CHAPMAN & HA LL/CRC Texts in Statis tical Science Series Series Editors Francesca Dominici, Harvard School of Public Health, USA Julian J. Faraway, University of Bath, U K Martin Tanner, Northwestern University, USA Jim Zidek, University of Br itish Columbia, Canada Statistical !eory: A Concise Introduction Statistics for Technology: A Course in Applied F. Abramovich and Y. Ritov Statistics, !ird Edition Practical Multivariate Analysis, Fifth Edition C. Chat!eld A. A!!, S. May, and V.A. Clark Analysis of Variance, Design, and Regression : Practical Statistics for Medical Research Linear Modeling for Unbalanced Data, D.G. Altman Second Edition R. Christensen Interpreting Data: A First Course in Statistics Bayesian Ideas and Data Analysis: An A.J.B. Anderson Introduction for Scientists and Statisticians Introduction to Probability with R R. Christensen, W. Johnson, A. Branscum, K. Baclawski and T.E. Hanson Linear Algebra and Matrix Analysis for Modelling Binary Data, Second Edition Statistics D. Collett S. Banerjee and A. Roy Modelling Survival Data in Medical Research, Mathematical Statistics: Basic Ideas and !ird Edition Selected Topics, Volume I, D. Collett Second Edition Introduction to Statistical Methods for P. J. Bickel and K. A. Doksum Clinical Trials Mathematical Statistics: Basic Ideas and T.D. Cook and D.L. DeMets Selected Topics, Volume II Applied Statistics: Principles and Examples P. J. Bickel and K. A. Doksum D.R. Cox and E.J. Snell Analysis of Categorical Data with R Multivariate Survival Analysis and Competing C. R. Bilder and T. M. Loughin Risks Statistical Methods for SPC and TQM M.
    [Show full text]
  • Notes on Stochastic Processes
    Notes on stochastic processes Paul Keeler March 20, 2018 This work is licensed under a “CC BY-SA 3.0” license. Abstract A stochastic process is a type of mathematical object studied in mathemat- ics, particularly in probability theory, which can be used to represent some type of random evolution or change of a system. There are many types of stochastic processes with applications in various fields outside of mathematics, including the physical sciences, social sciences, finance and economics as well as engineer- ing and technology. This survey aims to give an accessible but detailed account of various stochastic processes by covering their history, various mathematical definitions, and key properties as well detailing various terminology and appli- cations of the process. An emphasis is placed on non-mathematical descriptions of key concepts, with recommendations for further reading. 1 Introduction In probability and related fields, a stochastic or random process, which is also called a random function, is a mathematical object usually defined as a collection of random variables. Historically, the random variables were indexed by some set of increasing numbers, usually viewed as time, giving the interpretation of a stochastic process representing numerical values of some random system evolv- ing over time, such as the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule [120, page 7][51, page 46 and 47][66, page 1]. Stochastic processes are widely used as math- ematical models of systems and phenomena that appear to vary in a random manner. They have applications in many disciplines including physical sciences such as biology [67, 34], chemistry [156], ecology [16][104], neuroscience [102], and physics [63] as well as technology and engineering fields such as image and signal processing [53], computer science [15], information theory [43, page 71], and telecommunications [97][11][12].
    [Show full text]
  • Random Walk in Random Scenery (RWRS)
    IMS Lecture Notes–Monograph Series Dynamics & Stochastics Vol. 48 (2006) 53–65 c Institute of Mathematical Statistics, 2006 DOI: 10.1214/074921706000000077 Random walk in random scenery: A survey of some recent results Frank den Hollander1,2,* and Jeffrey E. Steif 3,† Leiden University & EURANDOM and Chalmers University of Technology Abstract. In this paper we give a survey of some recent results for random walk in random scenery (RWRS). On Zd, d ≥ 1, we are given a random walk with i.i.d. increments and a random scenery with i.i.d. components. The walk and the scenery are assumed to be independent. RWRS is the random process where time is indexed by Z, and at each unit of time both the step taken by the walk and the scenery value at the site that is visited are registered. We collect various results that classify the ergodic behavior of RWRS in terms of the characteristics of the underlying random walk (and discuss extensions to stationary walk increments and stationary scenery components as well). We describe a number of results for scenery reconstruction and close by listing some open questions. 1. Introduction Random walk in random scenery is a family of stationary random processes ex- hibiting amazingly rich behavior. We will survey some of the results that have been obtained in recent years and list some open questions. Mike Keane has made funda- mental contributions to this topic. As close colleagues it has been a great pleasure to work with him. We begin by defining the object of our study. Fix an integer d ≥ 1.
    [Show full text]
  • Generalized Bernoulli Process with Long-Range Dependence And
    Depend. Model. 2021; 9:1–12 Research Article Open Access Jeonghwa Lee* Generalized Bernoulli process with long-range dependence and fractional binomial distribution https://doi.org/10.1515/demo-2021-0100 Received October 23, 2020; accepted January 22, 2021 Abstract: Bernoulli process is a nite or innite sequence of independent binary variables, Xi , i = 1, 2, ··· , whose outcome is either 1 or 0 with probability P(Xi = 1) = p, P(Xi = 0) = 1 − p, for a xed constant p 2 (0, 1). We will relax the independence condition of Bernoulli variables, and develop a generalized Bernoulli process that is stationary and has auto-covariance function that obeys power law with exponent 2H − 2, H 2 (0, 1). Generalized Bernoulli process encompasses various forms of binary sequence from an independent binary sequence to a binary sequence that has long-range dependence. Fractional binomial random variable is dened as the sum of n consecutive variables in a generalized Bernoulli process, of particular interest is when its variance is proportional to n2H , if H 2 (1/2, 1). Keywords: Bernoulli process, Long-range dependence, Hurst exponent, over-dispersed binomial model MSC: 60G10, 60G22 1 Introduction Fractional process has been of interest due to its usefulness in capturing long lasting dependency in a stochas- tic process called long-range dependence, and has been rapidly developed for the last few decades. It has been applied to internet trac, queueing networks, hydrology data, etc (see [3, 7, 10]). Among the most well known models are fractional Gaussian noise, fractional Brownian motion, and fractional Poisson process. Fractional Brownian motion(fBm) BH(t) developed by Mandelbrot, B.
    [Show full text]
  • Particle Filtering Within Adaptive Metropolis Hastings Sampling
    Particle filtering within adaptive Metropolis-Hastings sampling Ralph S. Silva Paolo Giordani School of Economics Research Department University of New South Wales Sveriges Riksbank [email protected] [email protected] Robert Kohn∗ Michael K. Pitt School of Economics Economics Department University of New South Wales University of Warwick [email protected] [email protected] October 29, 2018 Abstract We show that it is feasible to carry out exact Bayesian inference for non-Gaussian state space models using an adaptive Metropolis-Hastings sampling scheme with the likelihood approximated by the particle filter. Furthermore, an adaptive independent Metropolis Hastings sampler based on a mixture of normals proposal is computation- ally much more efficient than an adaptive random walk Metropolis proposal because the cost of constructing a good adaptive proposal is negligible compared to the cost of approximating the likelihood. Independent Metropolis-Hastings proposals are also arXiv:0911.0230v1 [stat.CO] 2 Nov 2009 attractive because they are easy to run in parallel on multiple processors. We also show that when the particle filter is used, the marginal likelihood of any model is obtained in an efficient and unbiased manner, making model comparison straightforward. Keywords: Auxiliary variables; Bayesian inference; Bridge sampling; Marginal likeli- hood. ∗Corresponding author. 1 Introduction We show that it is feasible to carry out exact Bayesian inference on the parameters of a general state space model by using the particle filter to approximate the likelihood and adaptive Metropolis-Hastings sampling to generate unknown parameters. The state space model can be quite general, but we assume that the observation equation can be evaluated analytically and that it is possible to generate from the state transition equation.
    [Show full text]
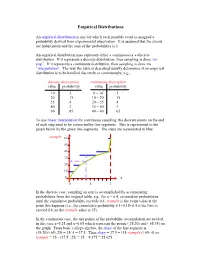
  • Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
    Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph.
    [Show full text]