A Tutorial on Bayesian Nonparametric Models
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Partnership As Experimentation: Business Organization and Survival in Egypt, 1910–1949
Yale University EliScholar – A Digital Platform for Scholarly Publishing at Yale Discussion Papers Economic Growth Center 5-1-2017 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç Timothy Guinnane Follow this and additional works at: https://elischolar.library.yale.edu/egcenter-discussion-paper-series Recommended Citation Artunç, Cihan and Guinnane, Timothy, "Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949" (2017). Discussion Papers. 1065. https://elischolar.library.yale.edu/egcenter-discussion-paper-series/1065 This Discussion Paper is brought to you for free and open access by the Economic Growth Center at EliScholar – A Digital Platform for Scholarly Publishing at Yale. It has been accepted for inclusion in Discussion Papers by an authorized administrator of EliScholar – A Digital Platform for Scholarly Publishing at Yale. For more information, please contact [email protected]. ECONOMIC GROWTH CENTER YALE UNIVERSITY P.O. Box 208269 New Haven, CT 06520-8269 http://www.econ.yale.edu/~egcenter Economic Growth Center Discussion Paper No. 1057 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç University of Arizona Timothy W. Guinnane Yale University Notes: Center discussion papers are preliminary materials circulated to stimulate discussion and critical comments. This paper can be downloaded without charge from the Social Science Research Network Electronic Paper Collection: https://ssrn.com/abstract=2973315 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç⇤ Timothy W. Guinnane† This Draft: May 2017 Abstract The relationship between legal forms of firm organization and economic develop- ment remains poorly understood. Recent research disputes the view that the joint-stock corporation played a crucial role in historical economic development, but retains the view that the costless firm dissolution implicit in non-corporate forms is detrimental to investment. -

A Model of Gene Expression Based on Random Dynamical Systems Reveals Modularity Properties of Gene Regulatory Networks†
A Model of Gene Expression Based on Random Dynamical Systems Reveals Modularity Properties of Gene Regulatory Networks† Fernando Antoneli1,4,*, Renata C. Ferreira3, Marcelo R. S. Briones2,4 1 Departmento de Informática em Saúde, Escola Paulista de Medicina (EPM), Universidade Federal de São Paulo (UNIFESP), SP, Brasil 2 Departmento de Microbiologia, Imunologia e Parasitologia, Escola Paulista de Medicina (EPM), Universidade Federal de São Paulo (UNIFESP), SP, Brasil 3 College of Medicine, Pennsylvania State University (Hershey), PA, USA 4 Laboratório de Genômica Evolutiva e Biocomplexidade, EPM, UNIFESP, Ed. Pesquisas II, Rua Pedro de Toledo 669, CEP 04039-032, São Paulo, Brasil Abstract. Here we propose a new approach to modeling gene expression based on the theory of random dynamical systems (RDS) that provides a general coupling prescription between the nodes of any given regulatory network given the dynamics of each node is modeled by a RDS. The main virtues of this approach are the following: (i) it provides a natural way to obtain arbitrarily large networks by coupling together simple basic pieces, thus revealing the modularity of regulatory networks; (ii) the assumptions about the stochastic processes used in the modeling are fairly general, in the sense that the only requirement is stationarity; (iii) there is a well developed mathematical theory, which is a blend of smooth dynamical systems theory, ergodic theory and stochastic analysis that allows one to extract relevant dynamical and statistical information without solving -

POISSON PROCESSES 1.1. the Rutherford-Chadwick-Ellis
POISSON PROCESSES 1. THE LAW OF SMALL NUMBERS 1.1. The Rutherford-Chadwick-Ellis Experiment. About 90 years ago Ernest Rutherford and his collaborators at the Cavendish Laboratory in Cambridge conducted a series of pathbreaking experiments on radioactive decay. In one of these, a radioactive substance was observed in N = 2608 time intervals of 7.5 seconds each, and the number of decay particles reaching a counter during each period was recorded. The table below shows the number Nk of these time periods in which exactly k decays were observed for k = 0,1,2,...,9. Also shown is N pk where k pk = (3.87) exp 3.87 =k! {− g The parameter value 3.87 was chosen because it is the mean number of decays/period for Rutherford’s data. k Nk N pk k Nk N pk 0 57 54.4 6 273 253.8 1 203 210.5 7 139 140.3 2 383 407.4 8 45 67.9 3 525 525.5 9 27 29.2 4 532 508.4 10 16 17.1 5 408 393.5 ≥ This is typical of what happens in many situations where counts of occurences of some sort are recorded: the Poisson distribution often provides an accurate – sometimes remarkably ac- curate – fit. Why? 1.2. Poisson Approximation to the Binomial Distribution. The ubiquity of the Poisson distri- bution in nature stems in large part from its connection to the Binomial and Hypergeometric distributions. The Binomial-(N ,p) distribution is the distribution of the number of successes in N independent Bernoulli trials, each with success probability p. -

Hierarchical Dirichlet Process Hidden Markov Model for Unsupervised Bioacoustic Analysis
Hierarchical Dirichlet Process Hidden Markov Model for Unsupervised Bioacoustic Analysis Marius Bartcus, Faicel Chamroukhi, Herve Glotin Abstract-Hidden Markov Models (HMMs) are one of the the standard HDP-HMM Gibbs sampling has the limitation most popular and successful models in statistics and machine of an inadequate modeling of the temporal persistence of learning for modeling sequential data. However, one main issue states [9]. This problem has been addressed in [9] by relying in HMMs is the one of choosing the number of hidden states. on a sticky extension which allows a more robust learning. The Hierarchical Dirichlet Process (HDP)-HMM is a Bayesian Other solutions for the inference of the hidden Markov non-parametric alternative for standard HMMs that offers a model in this infinite state space models are using the Beam principled way to tackle this challenging problem by relying sampling [lO] rather than Gibbs sampling. on a Hierarchical Dirichlet Process (HDP) prior. We investigate the HDP-HMM in a challenging problem of unsupervised We investigate the BNP formulation for the HMM, that is learning from bioacoustic data by using Markov-Chain Monte the HDP-HMM into a challenging problem of unsupervised Carlo (MCMC) sampling techniques, namely the Gibbs sampler. learning from bioacoustic data. The problem consists of We consider a real problem of fully unsupervised humpback extracting and classifying, in a fully unsupervised way, whale song decomposition. It consists in simultaneously finding the structure of hidden whale song units, and automatically unknown number of whale song units. We use the Gibbs inferring the unknown number of the hidden units from the Mel sampler to infer the HDP-HMM from the bioacoustic data. -

Contents-Preface
Stochastic Processes From Applications to Theory CHAPMAN & HA LL/CRC Texts in Statis tical Science Series Series Editors Francesca Dominici, Harvard School of Public Health, USA Julian J. Faraway, University of Bath, U K Martin Tanner, Northwestern University, USA Jim Zidek, University of Br itish Columbia, Canada Statistical !eory: A Concise Introduction Statistics for Technology: A Course in Applied F. Abramovich and Y. Ritov Statistics, !ird Edition Practical Multivariate Analysis, Fifth Edition C. Chat!eld A. A!!, S. May, and V.A. Clark Analysis of Variance, Design, and Regression : Practical Statistics for Medical Research Linear Modeling for Unbalanced Data, D.G. Altman Second Edition R. Christensen Interpreting Data: A First Course in Statistics Bayesian Ideas and Data Analysis: An A.J.B. Anderson Introduction for Scientists and Statisticians Introduction to Probability with R R. Christensen, W. Johnson, A. Branscum, K. Baclawski and T.E. Hanson Linear Algebra and Matrix Analysis for Modelling Binary Data, Second Edition Statistics D. Collett S. Banerjee and A. Roy Modelling Survival Data in Medical Research, Mathematical Statistics: Basic Ideas and !ird Edition Selected Topics, Volume I, D. Collett Second Edition Introduction to Statistical Methods for P. J. Bickel and K. A. Doksum Clinical Trials Mathematical Statistics: Basic Ideas and T.D. Cook and D.L. DeMets Selected Topics, Volume II Applied Statistics: Principles and Examples P. J. Bickel and K. A. Doksum D.R. Cox and E.J. Snell Analysis of Categorical Data with R Multivariate Survival Analysis and Competing C. R. Bilder and T. M. Loughin Risks Statistical Methods for SPC and TQM M. -

Notes on Stochastic Processes
Notes on stochastic processes Paul Keeler March 20, 2018 This work is licensed under a “CC BY-SA 3.0” license. Abstract A stochastic process is a type of mathematical object studied in mathemat- ics, particularly in probability theory, which can be used to represent some type of random evolution or change of a system. There are many types of stochastic processes with applications in various fields outside of mathematics, including the physical sciences, social sciences, finance and economics as well as engineer- ing and technology. This survey aims to give an accessible but detailed account of various stochastic processes by covering their history, various mathematical definitions, and key properties as well detailing various terminology and appli- cations of the process. An emphasis is placed on non-mathematical descriptions of key concepts, with recommendations for further reading. 1 Introduction In probability and related fields, a stochastic or random process, which is also called a random function, is a mathematical object usually defined as a collection of random variables. Historically, the random variables were indexed by some set of increasing numbers, usually viewed as time, giving the interpretation of a stochastic process representing numerical values of some random system evolv- ing over time, such as the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule [120, page 7][51, page 46 and 47][66, page 1]. Stochastic processes are widely used as math- ematical models of systems and phenomena that appear to vary in a random manner. They have applications in many disciplines including physical sciences such as biology [67, 34], chemistry [156], ecology [16][104], neuroscience [102], and physics [63] as well as technology and engineering fields such as image and signal processing [53], computer science [15], information theory [43, page 71], and telecommunications [97][11][12]. -

Random Walk in Random Scenery (RWRS)
IMS Lecture Notes–Monograph Series Dynamics & Stochastics Vol. 48 (2006) 53–65 c Institute of Mathematical Statistics, 2006 DOI: 10.1214/074921706000000077 Random walk in random scenery: A survey of some recent results Frank den Hollander1,2,* and Jeffrey E. Steif 3,† Leiden University & EURANDOM and Chalmers University of Technology Abstract. In this paper we give a survey of some recent results for random walk in random scenery (RWRS). On Zd, d ≥ 1, we are given a random walk with i.i.d. increments and a random scenery with i.i.d. components. The walk and the scenery are assumed to be independent. RWRS is the random process where time is indexed by Z, and at each unit of time both the step taken by the walk and the scenery value at the site that is visited are registered. We collect various results that classify the ergodic behavior of RWRS in terms of the characteristics of the underlying random walk (and discuss extensions to stationary walk increments and stationary scenery components as well). We describe a number of results for scenery reconstruction and close by listing some open questions. 1. Introduction Random walk in random scenery is a family of stationary random processes ex- hibiting amazingly rich behavior. We will survey some of the results that have been obtained in recent years and list some open questions. Mike Keane has made funda- mental contributions to this topic. As close colleagues it has been a great pleasure to work with him. We begin by defining the object of our study. Fix an integer d ≥ 1. -

Part 2: Basics of Dirichlet Processes 2.1 Motivation
CS547Q Statistical Modeling with Stochastic Processes Winter 2011 Part 2: Basics of Dirichlet processes Lecturer: Alexandre Bouchard-Cˆot´e Scribe(s): Liangliang Wang Disclaimer: These notes have not been subjected to the usual scrutiny reserved for formal publications. They may be distributed outside this class only with the permission of the Instructor. Last update: May 17, 2011 2.1 Motivation To motivate the Dirichlet process, let us consider a simple density estimation problem: modeling the height of UBC students. We are going to take a Bayesian approach to this problem, considering the parameters as random variables. In one of the most basic models, one would define a mean and variance random parameter θ = (µ, σ2), and a height random variable normally distributed conditionally on θ, with parameters θ.1 Using a single normal distribution is clearly a defective approach, since for example the male/female sub- populations create a skewness in the distribution, which cannot be capture by normal distributions: The solution suggested by this figure is to use a mixture of two normal distributions, with one set of parameters θc for each sub-population or cluster c ∈ {1, 2}. Pictorially, the model can be described as follows: 1- Generate a male/female relative frequence " " ~ Beta(male prior pseudo counts, female P.C) Mean height 2- Generate the sex of each student for each i for men Mult( ) !(1) x1 x2 x3 xi | " ~ " 3- Generate the mean height of each cluster c !(2) Mean height !(c) ~ N(prior height, how confident prior) for women y1 y2 y3 4- Generate student heights for each i yi | xi, !(1), !(2) ~ N(!(xi) ,variance) 1Yes, this has many problems (heights cannot be negative, normal assumption broken, etc). -

Lectures on Bayesian Nonparametrics: Modeling, Algorithms and Some Theory VIASM Summer School in Hanoi, August 7–14, 2015
Lectures on Bayesian nonparametrics: modeling, algorithms and some theory VIASM summer school in Hanoi, August 7–14, 2015 XuanLong Nguyen University of Michigan Abstract This is an elementary introduction to fundamental concepts of Bayesian nonparametrics, with an emphasis on the modeling and inference using Dirichlet process mixtures and their extensions. I draw partially from the materials of a graduate course jointly taught by Professor Jayaram Sethuraman and myself in Fall 2014 at the University of Michigan. Bayesian nonparametrics is a field which aims to create inference algorithms and statistical models, whose complexity may grow as data size increases. It is an area where probabilists, theoretical and applied statisticians, and machine learning researchers all make meaningful contacts and contributions. With the following choice of materials I hope to take the audience with modest statistical background to a vantage point from where one may begin to see a rich and sweeping panorama of a beautiful area of modern statistics. 1 Statistical inference The main goal of statistics and machine learning is to make inference about some unknown quantity based on observed data. For this purpose, one obtains data X with distribution depending on the unknown quantity, to be denoted by parameter θ. In classical statistics, this distribution is completely specified except for θ. Based on X, one makes statements about θ in some optimal way. This is the basic idea of statistical inference. Machine learning originally approached the inference problem through the lense of the computer science field of artificial intelligence. It was eventually realized that machine learning was built on the same theoretical foundation of mathematical statistics, in addition to carrying a strong emphasis on the development of algorithms. -

Generalized Bernoulli Process with Long-Range Dependence And
Depend. Model. 2021; 9:1–12 Research Article Open Access Jeonghwa Lee* Generalized Bernoulli process with long-range dependence and fractional binomial distribution https://doi.org/10.1515/demo-2021-0100 Received October 23, 2020; accepted January 22, 2021 Abstract: Bernoulli process is a nite or innite sequence of independent binary variables, Xi , i = 1, 2, ··· , whose outcome is either 1 or 0 with probability P(Xi = 1) = p, P(Xi = 0) = 1 − p, for a xed constant p 2 (0, 1). We will relax the independence condition of Bernoulli variables, and develop a generalized Bernoulli process that is stationary and has auto-covariance function that obeys power law with exponent 2H − 2, H 2 (0, 1). Generalized Bernoulli process encompasses various forms of binary sequence from an independent binary sequence to a binary sequence that has long-range dependence. Fractional binomial random variable is dened as the sum of n consecutive variables in a generalized Bernoulli process, of particular interest is when its variance is proportional to n2H , if H 2 (1/2, 1). Keywords: Bernoulli process, Long-range dependence, Hurst exponent, over-dispersed binomial model MSC: 60G10, 60G22 1 Introduction Fractional process has been of interest due to its usefulness in capturing long lasting dependency in a stochas- tic process called long-range dependence, and has been rapidly developed for the last few decades. It has been applied to internet trac, queueing networks, hydrology data, etc (see [3, 7, 10]). Among the most well known models are fractional Gaussian noise, fractional Brownian motion, and fractional Poisson process. Fractional Brownian motion(fBm) BH(t) developed by Mandelbrot, B. -
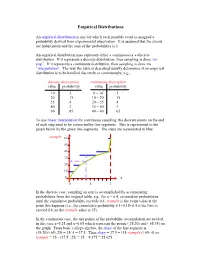
Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph. -

Diffusion Approximation for Bayesian Markov Chains
139 Diffusion Approximation for Bayesian Markov Chains Michael Duff [email protected] GatsbyComputational Neuroscience Unit, University College London, WCIN 3AR England Abstract state--~action--+state transitions of each kind with their associated expected immediate rewards. Ques- Given a Markovchain with uncertain transi- tion probabilities modelledin a Bayesian way, tions about value in this case reduce to questions about we investigate a technique for analytically ap- the distribution of transition frequency counts. These considerations lead to the focus of this paper--the esti- proximating the mean transition frequency mation of the meantransition-frequency counts associ- counts over a finite horizon. Conventional techniques for addressing this problemeither ated with a Markovchain (an MDPgoverned by a fixed require the enumeration of a set of general- policy), with unknowntransition probabilities (whose ized process "hyperstates" whosecardinality uncertainty distributions are updated in a Bayesian grows exponentially with the terminal hori- way), over a finite time-horizon. zon, or axe limited to the two-state case and This is a challenging problem in itself with a long expressed in terms of hypergeometric series. history, 1 and though in this paper we do not explic- Our approach makes use of a diffusion ap- itly pursue the moreambitious goal of developing full- proximation technique for modelling the evo- blown policy-iteration methods for computing optimal lution of information state componentsof the value functions and policies for uncertain MDP’s,one hyperstate process. Interest in this problem can envision using the approximation techniques de- stems from a consideration of the policy eval- scribed here as a basis for constructing effective static uation step of policy iteration algorithms ap- stochastic policies or receding-horizon approaches that plied to Markovdecision processes with un- repeatedly computesuch policies.