Diffusion Approximation for Bayesian Markov Chains
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Partnership As Experimentation: Business Organization and Survival in Egypt, 1910–1949
Yale University EliScholar – A Digital Platform for Scholarly Publishing at Yale Discussion Papers Economic Growth Center 5-1-2017 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç Timothy Guinnane Follow this and additional works at: https://elischolar.library.yale.edu/egcenter-discussion-paper-series Recommended Citation Artunç, Cihan and Guinnane, Timothy, "Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949" (2017). Discussion Papers. 1065. https://elischolar.library.yale.edu/egcenter-discussion-paper-series/1065 This Discussion Paper is brought to you for free and open access by the Economic Growth Center at EliScholar – A Digital Platform for Scholarly Publishing at Yale. It has been accepted for inclusion in Discussion Papers by an authorized administrator of EliScholar – A Digital Platform for Scholarly Publishing at Yale. For more information, please contact [email protected]. ECONOMIC GROWTH CENTER YALE UNIVERSITY P.O. Box 208269 New Haven, CT 06520-8269 http://www.econ.yale.edu/~egcenter Economic Growth Center Discussion Paper No. 1057 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç University of Arizona Timothy W. Guinnane Yale University Notes: Center discussion papers are preliminary materials circulated to stimulate discussion and critical comments. This paper can be downloaded without charge from the Social Science Research Network Electronic Paper Collection: https://ssrn.com/abstract=2973315 Partnership as Experimentation: Business Organization and Survival in Egypt, 1910–1949 Cihan Artunç⇤ Timothy W. Guinnane† This Draft: May 2017 Abstract The relationship between legal forms of firm organization and economic develop- ment remains poorly understood. Recent research disputes the view that the joint-stock corporation played a crucial role in historical economic development, but retains the view that the costless firm dissolution implicit in non-corporate forms is detrimental to investment. -

A Model of Gene Expression Based on Random Dynamical Systems Reveals Modularity Properties of Gene Regulatory Networks†
A Model of Gene Expression Based on Random Dynamical Systems Reveals Modularity Properties of Gene Regulatory Networks† Fernando Antoneli1,4,*, Renata C. Ferreira3, Marcelo R. S. Briones2,4 1 Departmento de Informática em Saúde, Escola Paulista de Medicina (EPM), Universidade Federal de São Paulo (UNIFESP), SP, Brasil 2 Departmento de Microbiologia, Imunologia e Parasitologia, Escola Paulista de Medicina (EPM), Universidade Federal de São Paulo (UNIFESP), SP, Brasil 3 College of Medicine, Pennsylvania State University (Hershey), PA, USA 4 Laboratório de Genômica Evolutiva e Biocomplexidade, EPM, UNIFESP, Ed. Pesquisas II, Rua Pedro de Toledo 669, CEP 04039-032, São Paulo, Brasil Abstract. Here we propose a new approach to modeling gene expression based on the theory of random dynamical systems (RDS) that provides a general coupling prescription between the nodes of any given regulatory network given the dynamics of each node is modeled by a RDS. The main virtues of this approach are the following: (i) it provides a natural way to obtain arbitrarily large networks by coupling together simple basic pieces, thus revealing the modularity of regulatory networks; (ii) the assumptions about the stochastic processes used in the modeling are fairly general, in the sense that the only requirement is stationarity; (iii) there is a well developed mathematical theory, which is a blend of smooth dynamical systems theory, ergodic theory and stochastic analysis that allows one to extract relevant dynamical and statistical information without solving -

POISSON PROCESSES 1.1. the Rutherford-Chadwick-Ellis
POISSON PROCESSES 1. THE LAW OF SMALL NUMBERS 1.1. The Rutherford-Chadwick-Ellis Experiment. About 90 years ago Ernest Rutherford and his collaborators at the Cavendish Laboratory in Cambridge conducted a series of pathbreaking experiments on radioactive decay. In one of these, a radioactive substance was observed in N = 2608 time intervals of 7.5 seconds each, and the number of decay particles reaching a counter during each period was recorded. The table below shows the number Nk of these time periods in which exactly k decays were observed for k = 0,1,2,...,9. Also shown is N pk where k pk = (3.87) exp 3.87 =k! {− g The parameter value 3.87 was chosen because it is the mean number of decays/period for Rutherford’s data. k Nk N pk k Nk N pk 0 57 54.4 6 273 253.8 1 203 210.5 7 139 140.3 2 383 407.4 8 45 67.9 3 525 525.5 9 27 29.2 4 532 508.4 10 16 17.1 5 408 393.5 ≥ This is typical of what happens in many situations where counts of occurences of some sort are recorded: the Poisson distribution often provides an accurate – sometimes remarkably ac- curate – fit. Why? 1.2. Poisson Approximation to the Binomial Distribution. The ubiquity of the Poisson distri- bution in nature stems in large part from its connection to the Binomial and Hypergeometric distributions. The Binomial-(N ,p) distribution is the distribution of the number of successes in N independent Bernoulli trials, each with success probability p. -

Contents-Preface
Stochastic Processes From Applications to Theory CHAPMAN & HA LL/CRC Texts in Statis tical Science Series Series Editors Francesca Dominici, Harvard School of Public Health, USA Julian J. Faraway, University of Bath, U K Martin Tanner, Northwestern University, USA Jim Zidek, University of Br itish Columbia, Canada Statistical !eory: A Concise Introduction Statistics for Technology: A Course in Applied F. Abramovich and Y. Ritov Statistics, !ird Edition Practical Multivariate Analysis, Fifth Edition C. Chat!eld A. A!!, S. May, and V.A. Clark Analysis of Variance, Design, and Regression : Practical Statistics for Medical Research Linear Modeling for Unbalanced Data, D.G. Altman Second Edition R. Christensen Interpreting Data: A First Course in Statistics Bayesian Ideas and Data Analysis: An A.J.B. Anderson Introduction for Scientists and Statisticians Introduction to Probability with R R. Christensen, W. Johnson, A. Branscum, K. Baclawski and T.E. Hanson Linear Algebra and Matrix Analysis for Modelling Binary Data, Second Edition Statistics D. Collett S. Banerjee and A. Roy Modelling Survival Data in Medical Research, Mathematical Statistics: Basic Ideas and !ird Edition Selected Topics, Volume I, D. Collett Second Edition Introduction to Statistical Methods for P. J. Bickel and K. A. Doksum Clinical Trials Mathematical Statistics: Basic Ideas and T.D. Cook and D.L. DeMets Selected Topics, Volume II Applied Statistics: Principles and Examples P. J. Bickel and K. A. Doksum D.R. Cox and E.J. Snell Analysis of Categorical Data with R Multivariate Survival Analysis and Competing C. R. Bilder and T. M. Loughin Risks Statistical Methods for SPC and TQM M. -

Notes on Stochastic Processes
Notes on stochastic processes Paul Keeler March 20, 2018 This work is licensed under a “CC BY-SA 3.0” license. Abstract A stochastic process is a type of mathematical object studied in mathemat- ics, particularly in probability theory, which can be used to represent some type of random evolution or change of a system. There are many types of stochastic processes with applications in various fields outside of mathematics, including the physical sciences, social sciences, finance and economics as well as engineer- ing and technology. This survey aims to give an accessible but detailed account of various stochastic processes by covering their history, various mathematical definitions, and key properties as well detailing various terminology and appli- cations of the process. An emphasis is placed on non-mathematical descriptions of key concepts, with recommendations for further reading. 1 Introduction In probability and related fields, a stochastic or random process, which is also called a random function, is a mathematical object usually defined as a collection of random variables. Historically, the random variables were indexed by some set of increasing numbers, usually viewed as time, giving the interpretation of a stochastic process representing numerical values of some random system evolv- ing over time, such as the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule [120, page 7][51, page 46 and 47][66, page 1]. Stochastic processes are widely used as math- ematical models of systems and phenomena that appear to vary in a random manner. They have applications in many disciplines including physical sciences such as biology [67, 34], chemistry [156], ecology [16][104], neuroscience [102], and physics [63] as well as technology and engineering fields such as image and signal processing [53], computer science [15], information theory [43, page 71], and telecommunications [97][11][12]. -

Random Walk in Random Scenery (RWRS)
IMS Lecture Notes–Monograph Series Dynamics & Stochastics Vol. 48 (2006) 53–65 c Institute of Mathematical Statistics, 2006 DOI: 10.1214/074921706000000077 Random walk in random scenery: A survey of some recent results Frank den Hollander1,2,* and Jeffrey E. Steif 3,† Leiden University & EURANDOM and Chalmers University of Technology Abstract. In this paper we give a survey of some recent results for random walk in random scenery (RWRS). On Zd, d ≥ 1, we are given a random walk with i.i.d. increments and a random scenery with i.i.d. components. The walk and the scenery are assumed to be independent. RWRS is the random process where time is indexed by Z, and at each unit of time both the step taken by the walk and the scenery value at the site that is visited are registered. We collect various results that classify the ergodic behavior of RWRS in terms of the characteristics of the underlying random walk (and discuss extensions to stationary walk increments and stationary scenery components as well). We describe a number of results for scenery reconstruction and close by listing some open questions. 1. Introduction Random walk in random scenery is a family of stationary random processes ex- hibiting amazingly rich behavior. We will survey some of the results that have been obtained in recent years and list some open questions. Mike Keane has made funda- mental contributions to this topic. As close colleagues it has been a great pleasure to work with him. We begin by defining the object of our study. Fix an integer d ≥ 1. -

Generalized Bernoulli Process with Long-Range Dependence And
Depend. Model. 2021; 9:1–12 Research Article Open Access Jeonghwa Lee* Generalized Bernoulli process with long-range dependence and fractional binomial distribution https://doi.org/10.1515/demo-2021-0100 Received October 23, 2020; accepted January 22, 2021 Abstract: Bernoulli process is a nite or innite sequence of independent binary variables, Xi , i = 1, 2, ··· , whose outcome is either 1 or 0 with probability P(Xi = 1) = p, P(Xi = 0) = 1 − p, for a xed constant p 2 (0, 1). We will relax the independence condition of Bernoulli variables, and develop a generalized Bernoulli process that is stationary and has auto-covariance function that obeys power law with exponent 2H − 2, H 2 (0, 1). Generalized Bernoulli process encompasses various forms of binary sequence from an independent binary sequence to a binary sequence that has long-range dependence. Fractional binomial random variable is dened as the sum of n consecutive variables in a generalized Bernoulli process, of particular interest is when its variance is proportional to n2H , if H 2 (1/2, 1). Keywords: Bernoulli process, Long-range dependence, Hurst exponent, over-dispersed binomial model MSC: 60G10, 60G22 1 Introduction Fractional process has been of interest due to its usefulness in capturing long lasting dependency in a stochas- tic process called long-range dependence, and has been rapidly developed for the last few decades. It has been applied to internet trac, queueing networks, hydrology data, etc (see [3, 7, 10]). Among the most well known models are fractional Gaussian noise, fractional Brownian motion, and fractional Poisson process. Fractional Brownian motion(fBm) BH(t) developed by Mandelbrot, B. -
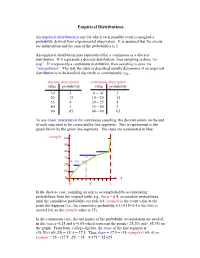
Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph. -

Last Passage Percolation and Traveling Fronts 2
LAST PASSAGE PERCOLATION AND TRAVELING FRONTS FRANCIS COMETS1,4, JEREMY QUASTEL2 AND ALEJANDRO F. RAM´IREZ3,4 Abstract. We consider a system of N particles with a stochastic dynamics introduced by Brunet and Derrida [7]. The particles can be interpreted as last passage times in directed percolation on 1,...,N of mean-field type. The particles remain grouped and move like a traveling front,{ subject to} discretization and driven by a random noise. As N increases, we obtain estimates for the speed of the front and its profile, for different laws of the driving noise. As shown in [7], the model with Gumbel distributed jumps has a simple structure. We establish that the scaling limit is a L´evy process in this case. We study other jump distributions. We prove a result showing that the limit for large N is stable under small perturbations of the Gumbel. In the opposite case of bounded jumps, a completely different behavior is found, where finite-size corrections are extremely small. 1. Definition of the model We consider the following stochastic process introduced by Brunet and Derrida [7]. It consists in a fixed number N 1 of particles on the real line, initially at the positions X (0),...,X (0). ≥ 1 N With ξi,j(s):1 i, j N,s 1 an i.i.d. family of real random variables, the positions evolve as { ≤ ≤ ≥ } Xi(t +1)= max Xj(t)+ ξi,j(t + 1) . (1.1) 1≤j≤N The components of the N-vector X(t)=(Xi(t), 1 i N) are not ordered. -

A Tutorial on Bayesian Nonparametric Models
A Tutorial on Bayesian Nonparametric Models Samuel J. Gershman1 and David M. Blei2 1Department of Psychology and Neuroscience Institute, Princeton University 2Department of Computer Science, Princeton University August 5, 2011 Abstract A key problem in statistical modeling is model selection, how to choose a model at an appropriate level of complexity. This problem appears in many settings, most prominently in choosing the number of clusters in mixture models or the number of factors in factor analysis. In this tutorial we describe Bayesian nonparametric methods, a class of methods that side-steps this issue by allowing the data to determine the complexity of the model. This tutorial is a high-level introduction to Bayesian nonparametric methods and contains several examples of their application. 1 Introduction How many classes should I use in my mixture model? How many factors should I use in factor analysis? These questions regularly exercise scientists as they explore their data. Most scientists address them by first fitting several models, with different numbers of clusters or factors, and then selecting one using model comparison metrics (Claeskens and Hjort, 2008). Model selection metrics usually include two terms. The first term measures how well the model fits the data. The second term, a complexity penalty, favors simpler models (i.e., ones with fewer components or factors). Bayesian nonparametric (BNP) models provide a different approach to this problem (Hjort et al., 2010). Rather than comparing models that vary in complexity, the BNP approach is to fit a single model that can adapt its complexity to the data. Furthermore, BNP models allow the complexity to grow as more data are observed, such as when using a model to perform prediction. -

Asymptotics for Dependent Bernoulli Random Variables
Statistics and Probability Letters 82 (2012) 455–463 Contents lists available at SciVerse ScienceDirect Statistics and Probability Letters journal homepage: www.elsevier.com/locate/stapro Asymptotics for dependent Bernoulli random variables Lan Wu a, Yongcheng Qi b, Jingping Yang a,∗ a LMAM, Department of Financial Mathematics, Center for Statistical Science, Peking University, Beijing 100871, China b Department of Mathematics and Statistics, University of Minnesota Duluth, 1117 University Drive, Duluth, MN 55812, USA article info a b s t r a c t Article history: This paper considers a sequence of Bernoulli random variables which are dependent in a Received 25 March 2011 way that the success probability of a trial conditional on the previous trials depends on Received in revised form 5 December 2011 the total number of successes achieved prior to the trial. The paper investigates almost Accepted 5 December 2011 sure behaviors for the sequence and proves the strong law of large numbers under weak Available online 14 December 2011 conditions. For linear probability functions, the paper also obtains the strong law of large numbers, the central limit theorems and the law of the iterated logarithm, extending the MSC: results by James et al.(2008). 60F15 ' 2011 Elsevier B.V. All rights reserved. Keywords: Dependent Bernoulli random variables Strong law of large numbers Central limit theorem Law of the iterated logarithm 1. Introduction Consider a sequence of Bernoulli random variables fXn; n ≥ 1g, which are dependent in a way that the success probability of a trial conditional on the previous trials depends on the total number of successes achieved to that point. -

Markovian Banditsgittins1979bandit
Markovian Bandits[1] Manyou Ma [email protected] Machine Learning Reading Group (MLRG 2019) Jul 31, 2019 Bandit Process Theorems Calculations of DAIs Applications Conclusions Outline Bandit Process Markov Decision Process (MDP) Bandit Process Theorems Forwards Induction Theorem and the DAI Theorem Stopping Sets Calculations of DAIs Two Simple Cases for Calculating DAI General Method for Calculating DAI Applications Scheduling Problem Multi-Armed Bandit Problem Conclusions 2 / 34 Bandit Process Theorems Calculations of DAIs Applications Conclusions Motivation I Consider the modifications below: I Bandit 1: f10; 2; 9; 7; 6; 0; 0; 0;:::g I Bandit 2: f5; 4; 3; 9; 1; 0; 0; 0;:::g hPT−1 t i I What is the policy that maximized lim E a rit (ιit ) T−!1 t=0 I a = 0.1: “Future is not so important” 0 1 2 3 4 5 6 I 10a + 5a + 4a + 3a + 9a + 2a + 8a + ::: I a = 0.9: “Future is (almost) as important as the present" 0 1 2 3 4 5 6 I 10a + 2a + 8a + 7a + 6a + 5a + 4a + ::: I a = 0.5: “Future is somewhat important" 0 1 2 3 4 5 6 I 10a + 5a + 2a + 8a + 7a + 6a + 4a + ::: 3 / 34 Bandit Process Theorems Calculations of DAIs Applications Conclusions Outline Bandit Process Markov Decision Process (MDP) Bandit Process Theorems Forwards Induction Theorem and the DAI Theorem Stopping Sets Calculations of DAIs Two Simple Cases for Calculating DAI General Method for Calculating DAI Applications Scheduling Problem Multi-Armed Bandit Problem Conclusions 4 / 34 Bandit Process Theorems Calculations of DAIs Applications Conclusions Markov Decision Process (MDP) I State: Defined on a state space Θ and σ-algebra X of subsets of Θ which includes every subset of consisting just one element of Θ I Action: When the process is in state x, the set of control may be applied: Ω(x).