DOCSLIB.ORG

On the Role of Protons in the Reactivation of Acetylcholinesterase: Quantum and Molecular Mechanics Studies

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
On the Role of Protons in the Reactivation of Acetylcholinesterase: Quantum and Molecular Mechanics Studies Université Pierre et Marie Curie Ecole doctoral de Chimie Moléculaire de Paris Centre Institut Parisien de Chimie Moléculaire/ Equipe MACO On the Role of Protons in the Reactivation of Acetylcholinesterase: Quantum and Molecular Mechanics Studies Présentée par : Thomas Driant Pour obtenir le grade de Docteur de l’université Pierre et Marie Curie Soutenance publique prévue le 22 septembre 2017 Devant un jury composé de : Madame Isabelle NAVIZET Professeur Rapporteur Monsieur Sam de VISSER Professeur Rapporteur Madame Shina Caroline Professeur Examinateur Lynn KAMERLIN Monsieur Florian NACHON Ingénieur d'études et Examinateur de fabrications HDR Monsieur Philippe KAROYAN Professeur Examinateur Monsieur Matthieu SOLLOGOUB Professeur Examinateur Monsieur Etienne DERAT Maître de Conférences HDR Directeur de thèse Acknowledgments My PhD Project was carried out at the Institut Parisien de Chimie Moléculaire, directed by Doctor Corinne Aubert. I worked as a member of the MACO team directed by Professor Louis Fensterbank. Firstly, I would like to address sincere thanks to Professor Isabelle Navizet, Professor Sam de Visser, Professor Shina Caroline Lynn Kamerlin, Professor Philippe Karoyan, Docteur Florian Nachon, and Professeur Matthieu Sollogoub for accepting to review my thesis and be part of my Jury. I am especially grateful to Doctor Etienne Derat for trusting me with this project. Looking back at my progress and maturation as a researcher I am proud of what I achieved and have you to thank for it. You have always been available for me to help me, guide me, teach me, and discuss the project. I am honoured by the confidence you put in me and I hope to have risen to the opportunity you have given me three years ago. I am also grateful to Professor Shina Caroline Lynn Kamerlin for hosting me in her team in Uppsala University for three months. I thank you for the substantial contribution you have made to my scientific growth throughout our collaboration. I also thank all the members of both the MACO team and the team of the Kamerlin lab, you are wonderful colleagues and I deeply enjoyed working with all of you. Finally, I would like to thank my friends, my family and Anne for their love and support during those three years. 3 Table of Contents ACKNOWLEDGMENTS ............................................................................................ 3 TABLE OF CONTENTS .............................................................................................. 4 GENERAL INTRODUCTION .................................................................................... 11 I. Biological significance of acetylcholinesterase ........................................................ 11 I.1. Role as a mediator of signal transmission .................................................................... 11 I.2. Target of nerve agents.................................................................................................. 13 II. Scope of this work .................................................................................................. 15 CHAPTER 1: INTRODUCTION ON ACETYLCHOLINESTERASE: STRUCTURE, FUNCTION, AND MECHANISM .............................................................................. 19 I. Structure of acetylcholinesterase ........................................................................... 19 I.1. Active site ..................................................................................................................... 23 I.2. Enzyme channel of AChE .............................................................................................. 29 II. Activity of acetylcholinesterase .............................................................................. 38 II.1. Regular catalytic activity ............................................................................................... 38 II.2. Inhibition by organophosphates .................................................................................. 40 II.3. Reactivation of acetylcholinesterase............................................................................ 46 III. Molecular simulations of AChE ............................................................................... 54 III.1. Regular catalytic activity ............................................................................................... 54 III.2. Inhibition by nerve agents ............................................................................................ 66 III.3. Reactivation by oximes ................................................................................................. 76 IV. Conclusions on acetylcholinesterase literature ....................................................... 84 CHAPTER 2: INTRODUCTION TO THE COMPUTATIONAL METHODS ..................... 87 I. Quantum mechanics .............................................................................................. 87 I.1. From molecular orbital method to Hartree-Fock theory ............................................. 88 I.2. Density functional theory ............................................................................................. 93 I.3. Valence bond theory .................................................................................................... 97 II. Molecular mechanics ............................................................................................. 99 II.1. Classical force fields ...................................................................................................... 99 II.2. Polarizable force fields ............................................................................................... 101 II.3. Molecular dynamics ................................................................................................... 103 II.4. Constant pH Molecular Dynamics .............................................................................. 104 4 II.5. Empirical Valence Bond .............................................................................................. 105 III. QM/MM ................................................................................................................ 87 III.1. Additive or Subtractive ............................................................................................... 109 III.2. Boundary scheme ....................................................................................................... 111 III.3. Interactions between QM and MM ............................................................................ 113 III.4. How to set up QM/MM simulations .......................................................................... 114 IV. Conclusion ............................................................................................................ 118 CHAPTER 3: TO DIVIDE AND CONQUER .............................................................. 121 I. Introduction .......................................................................................................... 121 II. Minimal model...................................................................................................... 124 III. The role of Glu334 ................................................................................................. 128 IV. The oxyanionic hole .............................................................................................. 131 V. The aromatic rings in the active site of AChE ......................................................... 136 V.1. Benzene ...................................................................................................................... 137 V.2. Phenol ......................................................................................................................... 144 V.3. Indole .......................................................................................................................... 150 VI. Discussion ............................................................................................................. 156 VII. Conclusions ........................................................................................................... 160 CHAPTER 4: QM/MM SIMULATIONS OF ACETYLCHOLINESTERASE REACTIVATION BY 2-PAM ............................................................................................................ 163 I. Computational details ........................................................................................... 163 II. Destabilization of the frontier orbitals of the systems ............................................ 169 III. Orientation of 2-PAM ............................................................................................ 173 IV. Study of the protonation state of Glu334 .............................................................. 173 V. VX-inhibited AChE reactivation by 2-PAM .............................................................. 175 V.1. Reactivation of AChE with an unprotonated Glu202 ................................................. 176 V.2. Reactivation of AChE with a protonated Glu202 ....................................................... 179 V.3. Reactivation with an unprotonated His447 and a protonated Glu202 ..................... 181 V.4. QM model confirmation ............................................................................................. 182 V.5. Alternate approach of 2-PAM towards the phosphorus ............................................ 184 VI. Deprotonation of 2-PAM in the active site of AChE ...............................................
Load more

Recommended publications
  • Protein Complex Formation by Acetylcholinesterase and the Neurotoxin Fasciculin-2 Appears to Involve an Induced-Fit Mechanism
    Protein complex formation by acetylcholinesterase and the neurotoxin fasciculin-2 appears to involve an induced-fit mechanism Jennifer M. Bui†‡ and J. Andrew McCammon†§ †Department of Chemistry and Biochemistry, Howard Hughes Medical Institute, and §Department of Pharmacology, University of California at San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0365 Edited by Jose N. Onuchic, University of California at San Diego, La Jolla, CA, and approved August 22, 2006 (received for review June 27, 2006) Specific, rapid association of protein complexes is essential for all forms of cellular existence. The initial association of two molecules in diffusion-controlled reactions is often influenced by the elec- trostatic potential. Yet, the detailed binding mechanisms of pro- teins highly depend on the particular system. A complete protein complex formation pathway has been delineated by using struc- tural information sampled over the course of the transformation reaction. The pathway begins at an encounter complex that is formed by one of the apo forms of neurotoxin fasciculin-2 (FAS2) and its high-affinity binding protein, acetylcholinesterase (AChE), followed by rapid conformational rearrangements into an inter- mediate complex that subsequently converts to the final complex as observed in crystal structures. Formation of the intermediate complex has also been independently captured in a separate 20-ns Fig. 1. Thermodynamic cycle for AB* complex formation reactions. A and B BIOPHYSICS molecular dynamics simulation of the encounter complex. Confor- molecules can be considered as any pair of interacting molecules. mational transitions between the apo and liganded states of FAS2 in the presence and absence of AChE are described in terms of their relative free energy profiles that link these two states.
    [Show full text]
  • Comparison of the Binding of Reversible Inhibitors to Human Butyrylcholinesterase and Acetylcholinesterase: a Crystallographic, Kinetic and Calorimetric Study
    Article Comparison of the Binding of Reversible Inhibitors to Human Butyrylcholinesterase and Acetylcholinesterase: A Crystallographic, Kinetic and Calorimetric Study Terrone L. Rosenberry 1, Xavier Brazzolotto 2, Ian R. Macdonald 3, Marielle Wandhammer 2, Marie Trovaslet-Leroy 2,†, Sultan Darvesh 4,5,6 and Florian Nachon 2,* 1 Departments of Neuroscience and Pharmacology, Mayo Clinic College of Medicine, Jacksonville, FL 32224, USA; [email protected] 2 Département de Toxicologie et Risques Chimiques, Institut de Recherche Biomédicale des Armées, 91220 Brétigny-sur-Orge, France; [email protected] (X.B.); [email protected] (M.W.); [email protected] (M.T.-L.) 3 Department of Diagnostic Radiology, Dalhousie University, Halifax, NS B3H 4R2, Canada; [email protected] 4 Department of Medical Neuroscience, Dalhousie University, Halifax, NS B3H 4R2, Canada; [email protected] 5 Department of Chemistry, Mount Saint Vincent University, Halifax, NS B3M 2J6, Canada 6 Department of Medicine (Neurology and Geriatric Medicine), Dalhousie University, Halifax, NS B3H 4R2, Canada * Correspondence: [email protected]; Tel.: +33-178-65-1877 † Deceased October 2016. Received: 26 October 2017; Accepted: 27 November 2017; Published: 29 November 2017 Abstract: Acetylcholinesterase (AChE) and butyrylcholinesterase (BChE) hydrolyze the neurotransmitter acetylcholine and, thereby, function as coregulators of cholinergic neurotransmission. Although closely related, these enzymes display very different substrate specificities that only partially overlap. This disparity is largely due to differences in the number of aromatic residues lining the active site gorge, which leads to large differences in the shape of the gorge and potentially to distinct interactions with an individual ligand. Considerable structural information is available for the binding of a wide diversity of ligands to AChE.
    [Show full text]
  • Anti-Cholinergic Alkaloids As Potential Therapeutic Agents for Alzheimer's Disease
    Indian Journal of Biochemistry & Biophysics Vol. 50, April 2013, pp. 120-125 Anti-cholinergic alkaloids as potential therapeutic agents for Alzheimer’s disease: An in silico approach Huma Naaz, Swati Singh, Veda P Pandey, Priyanka Singh and Upendra N Dwivedi* Bioinformatics Infrastructure Facility, Center of Excellence in Bioinformatics, Department of Biochemistry, University of Lucknow, Lucknow 226 007, India Received 10 September 2012; revised 25 January 2013 Alzheimer’s disease (AD), a progressive neurodegenerative disorder with many cognitive and neuropsychiatric symptoms is biochemically characterized by a significant decrease in the brain neurotransmitter acetylcholine (ACh). Plant-derived metabolites, including alkaloids have been reported to possess neuroprotective properties and are considered to be safe, thus have potential for developing effective therapeutic molecules for neurological disorders, such as AD. Therefore, in the present study, thirteen plant-derived alkaloids, namely pleiocarpine, kopsinine, pleiocarpamine (from Pleiocarpa mutica, family: Annonaceae), oliveroline, noroliveroline, liridonine, isooncodine, polyfothine, darienine (from Polyalthia longifolia, family: Apocynaceae) and eburnamine, eburnamonine, eburnamenine and geissoschizol (from Hunteria zeylanica, family: Apocynaceae) were analyzed for their anti-cholinergic action through docking with acetylcholinesterase (AChE) as target. Among the alkaloids, pleiocarpine showed promising anti-cholinergic potential, while its amino derivative showed about six-fold
    [Show full text]
  • Oximes: Inhibitors of Human Recombinant Acetylcholinesterase
    Int. J. Mol. Sci. 2013, 14, 16882-16900; doi:10.3390/ijms140816882 OPEN ACCESS International Journal of Molecular Sciences ISSN 1422-0067 www.mdpi.com/journal/ijms Article Oximes: Inhibitors of Human Recombinant Acetylcholinesterase. A Structure-Activity Relationship (SAR) Study Vendula Sepsova 1,†, Jana Zdarova Karasova 2,3, Jan Korabecny 1,3,†, Rafael Dolezal 3,†, Filip Zemek 1, Brian J. Bennion 4,† and Kamil Kuca 3,5,* 1 Department of Toxicology, Faculty of Military Health Sciences, University of Defence, Trebesska 1575, 500 01 Hradec Kralove, Czech Republic; E-Mails: [email protected] (V.S.); [email protected] (J.K.); [email protected] (F.Z.) 2 Department of Public Health, Faculty of Military Health Sciences, University of Defence, Trebesska 1575, 500 01 Hradec Kralove, Czech Republic; E-Mail: [email protected] 3 University Hospital, Biomedicinal Research Centre, Sokolska 581, 50005 Hradec Kralove, Czech Republic; E-Mail: [email protected] 4 Biosciences and Biotechnology Division, Lawrence Livermore National Laboratory, 7000 East Ave, Livermore, CA 94550, USA; E-Mail: [email protected] 5 Center of Advances Studies, Faculty of Military Health Sciences, University of Defence, Trebesska 1575, 500 01 Hradec Kralove, Czech Republic † These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +420-495-832-923; Fax: +420-495-518-094. Received: 8 May 2013; in revised form: 1 August 2013 / Accepted: 2 August 2013 / Published: 16 August 2013 Abstract: Acetylcholinesterase (AChE) reactivators were developed for the treatment of organophosphate intoxication. Standard care involves the use of anticonvulsants (e.g., diazepam), parasympatolytics (e.g., atropine) and oximes that restore AChE activity.
    [Show full text]
  • Viewed Journals
    Quinone Methide Precursors as Realkylators of Acetylcholinesterase for Post-aging Treatment of Organophosphorus Poisoning DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Qinggeng Zhuang Graduate Program in Chemistry The Ohio State University 2017 Dissertation Committee: Professor Christopher M. Hadad, Advisor Professor Thomas J. Magliery Professor Kotaro Nakanishi Copyrighted by Qinggeng Zhuang 2017 Abstract Acetylcholinesterase (AChE) is a serine hydrolase found in brain synapses, neuromuscular junctions (NMJs) and erythrocytes. Its role is to silence nerve impulses by selectively hydrolyzing acetylcholine, a neurotransmitter. Inhibition of AChE can lead to accumulation of acetylcholine at synapses and NMJs; if left untreated, the symptoms can lead to death. Organophosphorus (OP) chemical nerve agents are a type of suicide inhibitors for AChE, leading to phosphylation of the catalytic serine; such phosphylation blocks the critical nucleophilic serine residue in the active site. OPs have been used as pesticides and chemical warfare agents, and exposure to these compounds results in the death of thousands of people every year. Clinically, OP poisoning can be treated by a combination of anti-cholinergic drugs and oximes. However, a dealkylation process referred to as aging can follow inhibition. To date, the aged form of AChE has been recalcitrant to reactivation by any oxime. A straightforward post-aging treatment is to reverse aging by realkylation of the oxyanion on the phosphylated adduct. Quinone methides (QMs) and quinone methide precursor (QMP) have been reported as alkylators of proteins and phosphates. These previous reports imply the possibility to realkylate aged AChE using a QM or QMP.
    [Show full text]
  • Report from the 26Th Meeting on Toxinology,“Bioengineering Of
    toxins Meeting Report Report from the 26th Meeting on Toxinology, “Bioengineering of Toxins”, Organized by the French Society of Toxinology (SFET) and Held in Paris, France, 4–5 December 2019 Pascale Marchot 1,* , Sylvie Diochot 2, Michel R. Popoff 3 and Evelyne Benoit 4 1 Laboratoire ‘Architecture et Fonction des Macromolécules Biologiques’, CNRS/Aix-Marseille Université, Faculté des Sciences-Campus Luminy, 13288 Marseille CEDEX 09, France 2 Institut de Pharmacologie Moléculaire et Cellulaire, Université Côte d’Azur, CNRS, Sophia Antipolis, 06550 Valbonne, France; [email protected] 3 Bacterial Toxins, Institut Pasteur, 75015 Paris, France; michel-robert.popoff@pasteur.fr 4 Service d’Ingénierie Moléculaire des Protéines (SIMOPRO), CEA de Saclay, Université Paris-Saclay, 91191 Gif-sur-Yvette, France; [email protected] * Correspondence: [email protected]; Tel.: +33-4-9182-5579 Received: 18 December 2019; Accepted: 27 December 2019; Published: 3 January 2020 1. Preface This 26th edition of the annual Meeting on Toxinology (RT26) of the SFET (http://sfet.asso.fr/ international) was held at the Institut Pasteur of Paris on 4–5 December 2019. The central theme selected for this meeting, “Bioengineering of Toxins”, gave rise to two thematic sessions: one on animal and plant toxins (one of our “core” themes), and a second one on bacterial toxins in honour of Dr. Michel R. Popoff (Institut Pasteur, Paris, France), both sessions being aimed at emphasizing the latest findings on their respective topics. Nine speakers from eight countries (Belgium, Denmark, France, Germany, Russia, Singapore, the United Kingdom, and the United States of America) were invited as international experts to present their work, and other researchers and students presented theirs through 23 shorter lectures and 27 posters.
    [Show full text]
  • Structural Dynamics of Acetylcholinesterase and Its Implications in Reactivators Design Gianluca Santoni
    Structural dynamics of acetylcholinesterase and its implications in reactivators design Gianluca Santoni To cite this version: Gianluca Santoni. Structural dynamics of acetylcholinesterase and its implications in reactivators design. Biomolecules [q-bio.BM]. Université Grenoble Alpes, 2015. English. NNT : 2015GREAY019. tel-01212481 HAL Id: tel-01212481 https://tel.archives-ouvertes.fr/tel-01212481 Submitted on 6 Oct 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈSE Pour obtenir le grade de DOCTEUR DE L’UNIVERSITÉ DE GRENOBLE Spécialité : Physique pour les sciences du vivant Arrêté ministériel : 7 Aout 2006 Présentée par Gianluca SANTONI Thèse dirigée par Martin WEIK et codirigée par Florian NACHON préparée au sein de l’Institut de Biologie Structurale de Grenoble et de l’école doctorale de physique Structural dynamics of acetyl- cholinesterase and its implications in reactivator design Thèse soutenue publiquement le 30/01/2015, devant le jury composé de : Dr. Yves Bourne Directeur de recherche CNRS, AFMB Marseille, Rapporteur Dr. Etienne Derat Maitre de conference, Université Pierre et Marie Curie, Paris, Rapporteur Prof. Pierre-Yves Renard Professeur, Université de Normandie, Rouen, Examinateur Prof. Israel Silman Professeur, Weizmann Institute of Science,Rehovot, Examinateur Dr.
    [Show full text]
  • Acetylcholinesterase — New Roles for Gate a Relatively Long Distance to Reach the Active Site, Ache Is One of the Fastest an Old Actor Enzymes14
    PERSPECTIVES be answered regarding AChE catalysis; for OPINION example, the mechanism behind the extremely fast turnover rate of the enzyme. Despite the fact that the substrate has to navi- Acetylcholinesterase — new roles for gate a relatively long distance to reach the active site, AChE is one of the fastest an old actor enzymes14. One theory to explain this phe- nomenon has to do with the unusually strong electric field of AChE. It has been argued that Hermona Soreq and Shlomo Seidman this field assists catalysis by attracting the cationic substrate and expelling the anionic The discovery of the first neurotransmitter — understanding of AChE functions beyond the acetate product15. Site-directed mutagenesis, acetylcholine — was soon followed by the classical view and suggest the molecular basis however, has indicated that reducing the elec- discovery of its hydrolysing enzyme, for its functional heterogeneity. tric field has no effect on catalysis16.However, acetylcholinesterase. The role of the same approach has indicated an effect on acetylcholinesterase in terminating From early to recent discoveries the rate of association of fasciculin, a peptide acetylcholine-mediated neurotransmission The unique biochemical properties and phys- that can inhibit AChE17. made it the focus of intense research for iological significance of AChE make it an much of the past century. But the complexity interesting target for detailed structure–func- of acetylcholinesterase gene regulation and tion analysis. AChE-coding sequences have recent evidence for some of the long- been cloned so far from a range of evolution- a Peripheral Choline binding site suspected ‘non-classical’ actions of this arily diverse vertebrate and invertebrate binding enzyme have more recently driven a species that include insects, nematodes, fish, site profound revolution in acetylcholinesterase reptiles, birds and several mammals, among Active site research.
    [Show full text]
  • Pre-Synaptic Cholinergic and Cannabinergic Signaling in the Expression of Organophosphate Toxicity
    PRE-SYNAPTIC CHOLINERGIC AND CANNABINERGIC SIGNALING IN THE EXPRESSION OF ORGANOPHOSPHATE TOXICITY By PRAVEENA REDDY BAIREDDY Bachelor of Veterinary Science & Animal Husbandry Acharya N.G.Ranga Agricultural University Hyderabad, India. 2004 Submitted to the Faculty of the Graduate College of the Oklahoma State University in partial fulfillment of the requirements for the Degree of DOCTOR OF PHILOSOPHY December, 2009 PRE-SYNAPTIC CHOLINERGIC AND CANNABINERGIC SIGNALING IN THE EXPRESSION OF ORGANOPHOSPHATE TOXICITY Dissertation Approved: Dr. Carey N Pope Dr.Guangping Chen Dr. Diane McFarlane Dr. David R Wallance Dr. A. Gordon Emslie Dean of the Graduate College ii ACKNOWLEDGEMENTS I take this opportunity to sincerely express deep sense of gratitude to my major advisor Dr. Carey Pope. His constant support during the course of study is highly appreciated. I thank him for the constant encouragement, and critical suggestions. His expertise in field of toxicology, his approach towards research had helped me a lot during difficult times of my study. His confidence in me made me to work hard and become competitive. I convey my deep sense of gratitude and indebtedness for providing technical help in times of need. His advice helped me not only in research but also helped me to build a strong personality for myself. I would like to convey my gratitude to Drs. David Wallace, Guanping Chen and Diane McFarlane for serving as members of my committee. Their suggestions have definitely improved the quality of my research. Their critique during the course of my research is greatly appreciated. I owe my deep sense of gratitude to Dr. Jing Pope for training me in valuable techniques which were important for successful completion of my project.
    [Show full text]
  • The Guinea Pig Model for Organophosphate Toxicology and Therapeutic Development
    THE GUINEA PIG MODEL FOR ORGANOPHOSPHATE TOXICOLOGY AND THERAPEUTIC DEVELOPMENT A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy By Christopher Ruark B.S., Miami University, 2007 M.S., Wright State University, 2010 ______________________________________ 2015 Wright State University WRIGHT STATE UNIVERSITY GRADUATE SCHOOL May 2, 2015 I HEREBY RECOMMEND THAT THE DISSERTATION PREPARED UNDER MY SUPERVISION BY Christopher Ruark ENTITLED The Guinea Pig Model for Organophosphate Toxicology and Therapeutic Development BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Doctor of Philosophy. __________________________ Jeffery M. Gearhart, Ph.D. Dissertation Director ___________________________ Mill W. Miller Ph.D. Director, Biomedical Sciences Ph.D. Program ___________________________ Robert E. W. Fyffe, Ph.D. Committee on Vice President for Research and Final Examination Dean of the Graduate School ___________________________ Jeffery M. Gearhart, Ph.D. ___________________________ Adrian M. Corbett, Ph.D. ___________________________ James B. Lucot, Ph.D. ___________________________ Mateen M. Rizki, Ph.D. ___________________________ Gerald M. Alter, Ph.D. ABSTRACT Ruark, Christopher Ph.D., Biomedical Sciences Ph.D. program, Wright State University, 2015. The Guinea Pig Model for Organophosphate Toxicology and Therapeutic Development. Organophosphates (OPs) are highly toxic insecticides and nerve agents that have been designed to inhibit the hydrolysis of acetylcholine by binding to the serine active site of acetylcholinesterase (AChE). They are one of the most common causes of human poisoning worldwide and are frequently intentionally used in suicides in agricultural areas. For this reason, there is a need for therapeutics to rescue those from intoxication. Obvious ethical concerns prevent humans from being subjected to OP exposure for therapeutic efficacy and safety testing.
    [Show full text]
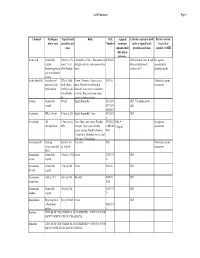
  • Coshh Database Page 1
    CoSHH database Page 1 Chemical Techniques Typical bench Risks Risk Assigned Controls required to work Further controls: where used quantities and Numbers maximum safely at typical bench Local rules / concs exposure limit quantities and concs separate CoSHH (8hr, unless otherwise Acetic acid General lab 500ml @ 10% Flammable@ 100%. This material is R10 R35 GLP for bench concs & vols. See separate reagent. stock. 5% in strongly corrosive and causes serious Always handle stock assessment for Destaining protein 500ml destain burns. volumes in FC decanting stocks gels in methanolic solution Acetic anhydride Acteylation of 25% in 100ul Poison. Corrosive. Causes severe R10-34 Undertake separate proteins. In situ final volume. burns. Harmful if swallowed or assessment hybridization O.25% in situ inhaled. Causes severe respiratory hybridization irritation. Eye contact may cause fix. serious irritation or burns Acetone General lab 500ml Highly flammable R11 R36 GLP. Use nitrile gloves reagent R37 R38 only R66 R67 Acetonitrile HPLC solvent 5 litres @ 20% Highly flammable. Toxic R23/24/2 GLP 5 Acrylamide Gel 1 litre stock @ Toxic. May cause cancer. Possible R23/24/2 MEL = See separate electrophoresis 40% teratogen. May cause heritable 5 R45/46 0.3mg/m3 assessment genetic damage. Readily absorbed R48 through skin. Inhalation may be fatal. May cause CNS damage. Actinomycin D Staining Stock of 1ml Very toxic R28 Undertake separate (intercalates with @ 1mg/ml assessment DNA) Ammonium General lab 100ml @ 9.5M Irritant R36/37/3 GLP acetate reagent 8 Ammonium
    [Show full text]
  • Design and Synthesis of N-Substituted-2
    *Manuscript Click here to view linked References 1 2 3 Design and synthesis of N-substituted-2-hydroxyiminoacetamides and 4 5 interactions with cholinesterases 6 7 8 a b b a a,* 9 Nikola Maraković , Anamarija Knežević , Vladimir Vinković , Zrinka Kovarik , Goran Šinko 10 11 a Institute for Medical Research and Occupational Health, Ksaverska cesta 2, HR-10 000 Zagreb, 12 Croatia 13 b Ruđer Bošković Institute, Bijenička cesta 54, HR-10 000 Zagreb, Croatia 14 15 16 17 Abstract 18 19 20 Within this study, we designed and synthesized four new oxime compounds of the N-substituted 2- 21 hydroxyiminoacetamide structure and evaluated their interactions with acetylcholinesterase (AChE) 22 23 and butyrylcholinesterase (BChE). Our aim was to explore the possibility of extending the dual-binding 24 25 mode of interaction between the enzyme and the inhibitor to a so-called triple-binding mode of 26 27 interaction through the introduction of an additional binding moiety. N-substituted 2- 28 29 hydroxyiminoacetamide 1 was prepared via BOP catalyzed amidation of hydroxyiminoacetic acid with 30 31 3-azido-1-phenylpropylamine. An azide group enabled us to prepare more elaborate structures 2 – 4 by 32 the copper-catalyzed azide-alkyne cycloaddition. The new compounds 1 – 4 differed in their presumed 33 34 AChE peripheral site binding moiety, which ranged from an azide group to functionalized heterocycles. 35 36 Molecular docking studies revealed that all three binding moieties are involved in the non-covalent 37 38 interactions with ChEs for all of the four compounds, albeit not always in the complete accordance 39 40 with the proposed hypothesis.
    [Show full text]