Deep-Seated Thrust Ring Faults Bound Elevated Mantle Plug Beneath Several Lunar Basins
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Geologic Structure of Shallow Maria
NASA CR. Photo Data Analysis S-221 NASA Contract NAS 9-13196 GEOLOGIC STRUCTURE OF SHALLOW MARIA Rene' A. De Hon, Principal Investigator John A. Waskom, Co-Investigator (NASA-CR-lq7qoo GEOLOGIC STahJCTUnF OF N76-17001 ISBALOW M1BIA-'(Arkansas Uni.v., mHiticelio.) 96 p BC $5.00' CSCL O3B Unclas G3/91, 09970- University of Arkansas at Monticello Monticello, Arkansas December 1975 Photo Data Analysis S-221 NASA Contract NAS 9-13196 GEOLOGIC STRUCTURE OF SHALLOW MARIA Rene' A. De Hon, Principal Investigator I John A. Waskom, Co-Investigator Un-iversity-of Arkansas-:at-.Monticl o Monticello, Arkansas December 1975 ABSTRACT Isopach maps and structural contour maps of the 0 0 eastern mare basins (30 N to 30 OS; 00 to 100 E) are constructed from measurements of partially buried craters. The data, which are sufficiently scattered to yield gross thickness variations, are restricted to shallow maria with less than 1500-2000 m of mare basalts. The average thickness of b-asalt in the irregular maria is between 200 and 400 m. Multiringed mascon basins are filled to various levels. The Serenitatis and Crisium basins have deeply flooded interiors and extensively flooded shelves. Mare basalts in the Nectaris basin fill only the innermost basin, and mare basalts in the Smythii basin occupy a small portion of the basin floor. Sinus Amoris, Mare Spumans, and Mare Undarum are partially filled troughs concentric to large circular basins. The Tranquillitatis and Fecunditatis are composite depressions containing basalts which flood degraded circular basins and adjacent terrain modified by the formation of nearby cir cular basins. -

TRANSIENT LUNAR PHENOMENA: REGULARITY and REALITY Arlin P
The Astrophysical Journal, 697:1–15, 2009 May 20 doi:10.1088/0004-637X/697/1/1 C 2009. The American Astronomical Society. All rights reserved. Printed in the U.S.A. TRANSIENT LUNAR PHENOMENA: REGULARITY AND REALITY Arlin P. S. Crotts Department of Astronomy, Columbia University, Columbia Astrophysics Laboratory, 550 West 120th Street, New York, NY 10027, USA Received 2007 June 27; accepted 2009 February 20; published 2009 April 30 ABSTRACT Transient lunar phenomena (TLPs) have been reported for centuries, but their nature is largely unsettled, and even their existence as a coherent phenomenon is controversial. Nonetheless, TLP data show regularities in the observations; a key question is whether this structure is imposed by processes tied to the lunar surface, or by terrestrial atmospheric or human observer effects. I interrogate an extensive catalog of TLPs to gauge how human factors determine the distribution of TLP reports. The sample is grouped according to variables which should produce differing results if determining factors involve humans, and not reflecting phenomena tied to the lunar surface. Features dependent on human factors can then be excluded. Regardless of how the sample is split, the results are similar: ∼50% of reports originate from near Aristarchus, ∼16% from Plato, ∼6% from recent, major impacts (Copernicus, Kepler, Tycho, and Aristarchus), plus several at Grimaldi. Mare Crisium produces a robust signal in some cases (however, Crisium is too large for a “feature” as defined). TLP count consistency for these features indicates that ∼80% of these may be real. Some commonly reported sites disappear from the robust averages, including Alphonsus, Ross D, and Gassendi. -

Radar Remote Sensing of Pyroclastic Deposits in the Southern Mare Serenitatis and Mare Vaporum Regions of the Moon Lynn M
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 114, E11004, doi:10.1029/2009JE003406, 2009 Click Here for Full Article Radar remote sensing of pyroclastic deposits in the southern Mare Serenitatis and Mare Vaporum regions of the Moon Lynn M. Carter,1 Bruce A. Campbell,1 B. Ray Hawke,2 Donald B. Campbell,3 and Michael C. Nolan4 Received 21 April 2009; revised 12 July 2009; accepted 3 August 2009; published 5 November 2009. [1] We use polarimetric radar observations to study the distribution, depth, and embedded rock abundance of nearside lunar pyroclastic deposits. Radar images were obtained for Mare Vaporum and the southern half of Mare Serenitatis; the imaged areas contain the large Rima Bode, Mare Vaporum, Sulpicius Gallus, and Taurus-Littrow pyroclastic deposits. Potential pyroclastic deposits at Rima Hyginus crater, the Tacquet Formation, and a dome in Mare Vaporum are also included. Data were acquired at S band (12.6 cm wavelength) using Arecibo Observatory and the Green Bank Telescope in a bistatic configuration. The S band images have resolutions between 20 and 100 m/pixel. The pyroclastic deposits appear dark to the radar and have low circular polarization ratios at S band wavelengths because they are smooth, easily penetrable by radar waves, and generally contain few embedded blocks. Changes in circular polarization ratio (CPR) across some of the pyroclastic deposits show areas with increased rock abundance as well as deposits that are shallower. Radar backscatter and CPR maps are used to identify fine-grained mantling deposits in cases where optical and near-infrared data are ambiguous about the presence of pyroclastics. -
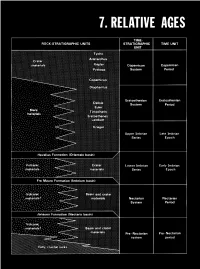
Relative Ages
CONTENTS Page Introduction ...................................................... 123 Stratigraphic nomenclature ........................................ 123 Superpositions ................................................... 125 Mare-crater relations .......................................... 125 Crater-crater relations .......................................... 127 Basin-crater relations .......................................... 127 Mapping conventions .......................................... 127 Crater dating .................................................... 129 General principles ............................................. 129 Size-frequency relations ........................................ 129 Morphology of large craters .................................... 129 Morphology of small craters, by Newell J. Fask .................. 131 D, method .................................................... 133 Summary ........................................................ 133 table 7.1). The first three of these sequences, which are older than INTRODUCTION the visible mare materials, are also dominated internally by the The goals of both terrestrial and lunar stratigraphy are to inte- deposits of basins. The fourth (youngest) sequence consists of mare grate geologic units into a stratigraphic column applicable over the and crater materials. This chapter explains the general methods of whole planet and to calibrate this column with absolute ages. The stratigraphic analysis that are employed in the next six chapters first step in reconstructing -

SMART-1 Lunar Highlights Bernard H
SMART-1 lunar highlights Bernard H. Foing & SMART-1 Project & Operations team, SMART-1 Science Technology Working Team, SMART-1 Impact Campaign Team http://sci.esa.int/smart-1/, www.esa.int BHF 2007 Europe to the Moon: spacecraft, launch, operations (ESA+ industry) Instruments PIs + TIs from 5 countries Co-Is from 13 ESA + 6 non European countries BHF 2007 Solar Electric Primary Propulsion: 7 g thrust, 60 liters Xenon to the Moon BHF 2007 SMART-1: With Sun power to the Moon on 60 liters of fuel BHF 2007 Solar Electric Propulsion to the Moon – Launched 27 Sept 2003 as Auxiliary passenger on Ariane 5 into Geostationary Transfer Orbit – Spiral out cruise (13.5 month): – lunar capture 15 November 2004, spiral down – arrival 15 March 05 science(450 -2900 km): commissioned spacecraft/instruments at Moon, nominal science mission March-July 05 – reboosting 2 aug-15 Sept 05 to increase orbit lifetime for extension phase until Aug 2006 BHF 2007 AMIE /SMART-1 End August 2006 Earth set & rise from the Moon X AMIE /SMART-1 May 21st, 2004 Earth view from ~70’000 km BHF 2007 First European Far Side Image of The Moon by AMIE/SMART-1 North Pole 12 Nov. 2004 BHF 2007 Moon Phase & Mission Extension MISSION EXTENSION Apolune Perilune Moon Radius BHF 2007 Sun SMART-1 light Reflecte d Sun Triple junction solar cells Multicolor microcamera light KA-band antenna Laser Link Communication X-Ray Spectrometer On-board computer Lithium ion batteries Infrared Spectrometer OBAN Platform Autonomy Technologies Miniaturisation BHF 2007 SMART-1 Science and Exploration Themes -

Geological Evolution of the Largest Shield Volcano Bearing Mare of The
52nd Lunar and Planetary Science Conference 2021 (LPI Contrib. No. 2548) 1827.pdf GEOLOGICAL EVOLUTION OF THE LARGEST SHIELD VOLCANO BEARING MARE OF THE MOON, MARE TRANQUILLITATIS: BASED ON DETAILED MORPHOLOGICAL, MINERALOGICAL, TOPOGRAPHIC STUDIES USING MULTIPLE DATA SETS. Henal Bhatt1, P. Chauhan2, Paras Solanki1, 1M. G. Science Institute, Ahmedabad 380009, India, 2Indian Institute of Remote Sensing, (ISRO), Dehradun, Uttarakhand, India. ([email protected] ) Introduction: In this work, we have analysed the Results and Discussions: Mare Tranquillitatis is irregular shaped Mare Tranquillitatis based on its delineated in to 22 spectral units based on IBD parameter morphology, mineralogy and topography to understand its analysis (Fig. 1). The band parameters analysis was geological evolution in the Lunar formation history. This conducted as per [8], [9], [10] suggest the abundance of area is very unique as it resides the largest shield volcano mafic silicate mixture, particular, mixture of olivine and of the Moon, compared to all the other circular mare basins medium to high calcium pyroxene bearing basaltic material at the near side of the Moon. It is located towards eastern in the area (Fig. 1). Details of this analysis is reported in the near side at 7°N, 30°E and is a Pre-Nectarian age basin [1]. [11]. Graphical trends suggests that basalts of eastern shield It is well known for Apollo 11 landing site and it shows mare would have been comparatively more pyroxene characteristic two basin ring structure [2], with diameter of bearing compared to the basalts from western deepest part, 800 km from east to west. which would have been more olivine bearing compared to the eastern shield mare basalt (Fig. -

Water on the Moon, III. Volatiles & Activity
Water on The Moon, III. Volatiles & Activity Arlin Crotts (Columbia University) For centuries some scientists have argued that there is activity on the Moon (or water, as recounted in Parts I & II), while others have thought the Moon is simply a dead, inactive world. [1] The question comes in several forms: is there a detectable atmosphere? Does the surface of the Moon change? What causes interior seismic activity? From a more modern viewpoint, we now know that as much carbon monoxide as water was excavated during the LCROSS impact, as detailed in Part I, and a comparable amount of other volatiles were found. At one time the Moon outgassed prodigious amounts of water and hydrogen in volcanic fire fountains, but released similar amounts of volatile sulfur (or SO2), and presumably large amounts of carbon dioxide or monoxide, if theory is to be believed. So water on the Moon is associated with other gases. Astronomers have agreed for centuries that there is no firm evidence for “weather” on the Moon visible from Earth, and little evidence of thick atmosphere. [2] How would one detect the Moon’s atmosphere from Earth? An obvious means is atmospheric refraction. As you watch the Sun set, its image is displaced by Earth’s atmospheric refraction at the horizon from the position it would have if there were no atmosphere, by roughly 0.6 degree (a bit more than the Sun’s angular diameter). On the Moon, any atmosphere would cause an analogous effect for a star passing behind the Moon during an occultation (multiplied by two since the light travels both into and out of the lunar atmosphere). -

Moon Viewing Guide
MMoooonn MMaapp What lunar features can you find? Use this Moon Map & Viewing Guide to explore different areas of the Moon - no binoculars needed! MMoooonn VViieewwiinngg GGuuiiddee A quick look at the Moon in the night sky – even without binoculars - shows light areas and dark areas that reveal lunar history. Can you find these features? Use the Moon Map (above) to help. Sea of Tranquility (Mare Tanquilitatus) – Formed when a giant t! nd I asteroid hit the Moon almost 4 billion years ago, this 500-mile wide Fou dark, smooth, circular basin is the site of the Apollo 11 landing in 1969. Sea of Rains (Mare Imbrium) – Imbrium Basin is the largest t! nd I basin on the Moon that was formed by a giant asteroid almost 4 Fou billion years ago. Sea of Serenity (Mare Serenitatis) – Apollo 17 astronauts t! sampled some of the oldest rocks on the Moon from edges of nd I Fou the Sea of Serenity. These ancient rocks formed in the Moon’s magma ocean. Lunar Highlands – The lighter areas on the Moon are the lunar t! highlands. These are the oldest regions on the Moon; they formed nd I Fou from the magma ocean. Because they are so old, they have been hit by impact craters many times, making the highlands very rough. Want an extra challenge? If you have a telescope or pair of binoculars, try finding these features: Appenine Mountains (Montes Apenninus) – Did you know there are mountain ranges on the Moon? The rims of the craters and t! nd I basins rise high above the Moon’s surface. -

ASTR110G Astronomy Laboratory Exercises C the GEAS Project 2020
ASTR110G Astronomy Laboratory Exercises c The GEAS Project 2020 ASTR110G Laboratory Exercises Lab 1: Fundamentals of Measurement and Error Analysis ...... ....................... 1 Lab 2: Observing the Sky ............................... ............................. 35 Lab 3: Cratering and the Lunar Surface ................... ........................... 73 Lab 4: Cratering and the Martian Surface ................. ........................... 97 Lab 5: Parallax Measurements and Determining Distances ... ....................... 129 Lab 6: The Hertzsprung-Russell Diagram and Stellar Evolution ..................... 157 Lab 7: Hubble’s Law and the Cosmic Distance Scale ........... ..................... 185 Lab 8: Properties of Galaxies .......................... ............................. 213 Appendix I: Definitions for Keywords ..................... .......................... 249 Appendix II: Supplies ................................. .............................. 263 Lab 1 Fundamentals of Measurement and Error Analysis 1.1 Introduction This laboratory exercise will serve as an introduction to all of the laboratory exercises for this course. We will explore proper techniques for obtaining and analyzing data, and practice plotting and analyzing data. We will discuss a scientific methodology for conducting exper- iments in which we formulate a question, predict the behavior of the system based on likely solutions, acquire relevant data, and then compare our predictions with the observations. You will have a chance to plan a short experiment, -

Apollo Over the Moon: a View from Orbit (Nasa Sp-362)
chl APOLLO OVER THE MOON: A VIEW FROM ORBIT (NASA SP-362) Chapter 1 - Introduction Harold Masursky, Farouk El-Baz, Frederick J. Doyle, and Leon J. Kosofsky [For a high resolution picture- click here] Objectives [1] Photography of the lunar surface was considered an important goal of the Apollo program by the National Aeronautics and Space Administration. The important objectives of Apollo photography were (1) to gather data pertaining to the topography and specific landmarks along the approach paths to the early Apollo landing sites; (2) to obtain high-resolution photographs of the landing sites and surrounding areas to plan lunar surface exploration, and to provide a basis for extrapolating the concentrated observations at the landing sites to nearby areas; and (3) to obtain photographs suitable for regional studies of the lunar geologic environment and the processes that act upon it. Through study of the photographs and all other arrays of information gathered by the Apollo and earlier lunar programs, we may develop an understanding of the evolution of the lunar crust. In this introductory chapter we describe how the Apollo photographic systems were selected and used; how the photographic mission plans were formulated and conducted; how part of the great mass of data is being analyzed and published; and, finally, we describe some of the scientific results. Historically most lunar atlases have used photointerpretive techniques to discuss the possible origins of the Moon's crust and its surface features. The ideas presented in this volume also rely on photointerpretation. However, many ideas are substantiated or expanded by information obtained from the huge arrays of supporting data gathered by Earth-based and orbital sensors, from experiments deployed on the lunar surface, and from studies made of the returned samples. -

Glossary of Lunar Terminology
Glossary of Lunar Terminology albedo A measure of the reflectivity of the Moon's gabbro A coarse crystalline rock, often found in the visible surface. The Moon's albedo averages 0.07, which lunar highlands, containing plagioclase and pyroxene. means that its surface reflects, on average, 7% of the Anorthositic gabbros contain 65-78% calcium feldspar. light falling on it. gardening The process by which the Moon's surface is anorthosite A coarse-grained rock, largely composed of mixed with deeper layers, mainly as a result of meteor calcium feldspar, common on the Moon. itic bombardment. basalt A type of fine-grained volcanic rock containing ghost crater (ruined crater) The faint outline that remains the minerals pyroxene and plagioclase (calcium of a lunar crater that has been largely erased by some feldspar). Mare basalts are rich in iron and titanium, later action, usually lava flooding. while highland basalts are high in aluminum. glacis A gently sloping bank; an old term for the outer breccia A rock composed of a matrix oflarger, angular slope of a crater's walls. stony fragments and a finer, binding component. graben A sunken area between faults. caldera A type of volcanic crater formed primarily by a highlands The Moon's lighter-colored regions, which sinking of its floor rather than by the ejection of lava. are higher than their surroundings and thus not central peak A mountainous landform at or near the covered by dark lavas. Most highland features are the center of certain lunar craters, possibly formed by an rims or central peaks of impact sites. -

Lunar Sourcebook : a User's Guide to the Moon
4 LUNAR SURFACE PROCESSES Friedrich Hörz, Richard Grieve, Grant Heiken, Paul Spudis, and Alan Binder The Moon’s surface is not affected by atmosphere, encounters with each other and with larger planets water, or life, the three major agents for altering throughout the lifetime of the solar system. These terrestrial surfaces. In addition, the lunar surface has orbital alterations are generally minor, but they not been shaped by recent geological activity, because ensure that, over geological periods, collisions with the lunar crust and mantle have been relatively cold other bodies will occur. and rigid throughout most of geological time. When such a collision happens, two outcomes are Convective internal mass transport, which dominates possible. If “target” and “projectile” are of comparable the dynamic Earth, is therefore largely absent on the size, collisional fragmentation and annihilation Moon, and so are the geological effects of such occurs, producing a large number of much smaller internal motions—volcanism, uplift, faulting, and fragments. If the target object is very large compared subduction—that both create and destroy surfaces on to the projectile, it behaves as an “infinite halfspace,” Earth. The great contrast between the ancient, stable and the result is an impact crater in the target body. Moon and the active, dynamic Earth is most clearly For collisions in the asteroid belt, many of the shown by the ages of their surfaces. Nearly 80% of the resulting collisional fragments or crater ejecta escape entire solid surface of Earth is <200 m.y. old. In the gravitational field of the impacted object; many of contrast, >99% of the lunar surface formed more than these fragments are then further perturbed into 3 b.y.