DOCSLIB.ORG

Part II: Symmetry Operations and Point Groups

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Part II: Symmetry Operations and Point Groups Part II: Symmetry Operations and Point Groups C734b C734b Symmetry Operations and 1 Point groups Definitions 1.- symmetry operations: leave a set of objects in indistinguishable configurations said to be equivalent -The identity operator, E is the “do nothing” operator. Therefore, its final configuration is not distinguishable from the initial one, but identical with it. 2.- symmetry element: a geometrical entity (line, plane or point) with respect to which one or more symmetry operations may be carried out. Four kinds of symmetry elements for molecular symmetry 1.) Plane operation = reflection in the plane 2.) Centre of symmetry or inversion centre: operation = inversion of all atoms through the centre 3.) Proper axis operation = one or more rotations about the axis 4.) Improper axis operation = one or more of the sequence rotation about the axis followed by reflection in a plane perpendicular (┴) to the rotation axis. C734b Symmetry Operations and 2 Point groups 1 1. Symmetry Plane and Reflection A plane must pass through a body, not be outside. Symbol = σ. The same symbol is used for the operation of reflecting through a plane σm as an operation means “carry out the reflection in a plane normal to m”. Take a point {e , e , e } along (xˆ, yˆ,zˆ) ∴ 1 2 3 ⎧ − ⎫ σ {e , e , e } = {-e , e , e } ≡ ⎨e1 , e 2 , e 3 ⎬ x 1 2 3 1 2 3 ⎩ ⎭ Often the plane itself is specified rather than the normal. σ = σ means “reflect in a plane containing the y- and z-, usually ⇒ x yz called the yz olane C734b Symmetry Operations and 3 Point groups -atoms lying in a plane is a special case since reflection through a plane doesn’t move the atoms. Consequently all planar molecules have at least one plane of symmetry ≡ molecular plane Note: σ produces an equivalent configuration. σ2 = σσ produces an identical configuration with the original. ∴ σ2 = E ∴ σn = E for n even; n = 2, 4, 6,… σn = σ for n odd; n = 3, 5, 7,… C734b Symmetry Operations and 4 Point groups 2 Some molecules have no σ-planes: S O F Cl Linear molecules have an infinite number of planes containing the bond axis. X Y Many molecules have a number of planes which lie somewhere between these two extremes: Example: H O 2 planes; 1 molecular plane + 2 O the other bisecting the H-O-H group H H C734b Symmetry Operations and 5 Point groups Example: NH3 N 3 planes containing on N-H bond and H H bisecting opposite HNH group H 4 planes; I molecular plane + Example: BCl3 Cl Cl 3 containing a B-Cl bond and B bisecting the opposite Cl-B-Cl group Cl - 5 planes; 1 molecular plane + Example: [AuCl ]- 4 Cl Cl 4 planes; 2 containing Cl-Au-Cl square planar Au + 2 bisecting the Cl-Au-Cl groups. Cl Cl C734b Symmetry Operations and 6 Point groups 3 Tetrahedral molecules like CH4 have 6 planes. H C H H H Octahedral molecules like SF6 have 9 planes in total F F F S F F F C734b Symmetry Operations and 7 Point groups 2.) Inversion Centre -Symbol = i - operation on a point {e1, e2, e3} i{e1, e2, e3} = {-e1, -e2, -e3} z z i e -e 3 1 -e 2 e y 2 y e -e 1 3 x x C734b Symmetry Operations and 8 Point groups 4 -If an atom exists at the inversion centre it is the only atom which will not move upon inversion. -All other atoms occur in pairs which are “twins”. This means no inversion centre for molecules containing an odd number of more than one species of atoms. i2 = ii = E ⇒ in = E n even in = i n odd C734b Symmetry Operations and 9 Point groups Example: 2 1 4 - 3 - Cl Cl Cl Cl Au i Au Cl Cl Cl Cl 3 4 1 2 - but H H or H H C H H H H H have no inversion centre even though in the methane case the number of Hs is even C734b Symmetry Operations and 10 Point groups 5 3. Proper Axes and Proper Rotations - A proper rotation or simply rotation is effected by an operator R(Φ,n) which means “carry out a rotation with respect to a fixed axis through an angle Φ described by some unit vector n”. ’ For example: R(π/4, x){e1, e2, e3} = {e1’, e2 , e3’} z z R(π/4, x) 45o e ' e 2 3 e ' 45o 3 e y 2 y e 1 e ' 1 x x C734b Symmetry Operations and 11 Point groups Take the following as the convention: a rotation is positive if looking down axis of rotation the rotation appears to be counterclockwise. More common symbol for rotation operator is Cn where n is the order of the axis. C means “carry out a rotation through an angle of Φ = 2π/n” ⇒ n R(π/4) ≡ C R(π/2) = C R(π) = C etc. ∴ 8 4 2 C2 is also called a binary rotation. C734b Symmetry Operations and 12 Point groups 6 Product of symmetry operators means: “carry out the operation successively beginning with the one on the right”. C C = C 2 = C = R(π, n) ∴ 4 4 4 2 k k (Cn) = Cn = R(Φ, n); Φ = 2πk/n C -k = R(-Φ, n); Φ = -2πk/n ∴ n k -k k+(-k) 0 Cn Cn = Cn = Cn ≡ E C -k is the inverse of C k ⇒ n n C734b Symmetry Operations and 13 Point groups Example: 3 2 1 C3 ≡ C3 = rotation by 2π/3 2 1 1 3 I = 120o II C3 axis is perpendicular to the plane of the equilateral triangle. 2 1 2 C3C3 = C3 = rotation by 4π/3 3 2 1 3 = 240o I III C734b Symmetry Operations and 14 Point groups 7 But 1 2 -1 C3 = rotation by -2π/3 3 2 1 3 III I = -120o C 2 = C -1 ∴ 3 3 2 2 3 C3 = rotation by 2π 3 1 3 1 I I = 360o C 3 = E ∴ 3 C734b Symmetry Operations and 15 Point groups 4 What about C3 ? 3 2 4 C3 = C3C3C3C3 2 1 1 II I 3 C 4 = C ∴ 3 3 only C , C 2, E are separate and distinct operations ⇒ 3 3 Similar arguments can be applied to any proper axis of order n C734b Symmetry Operations and 16 Point groups 8 Example: C6: C6; 2 C6 ≡ C3 3 C6 ≡ C2 4 -2 -1 C6 ≡ C6 ≡ C3 5 -1 C6 ≡ C6 6 C6 ≡ E Note: for Cn n odd the existence of one C2 axis perpendicular to or σ containing Cn implies n-1 more separate (that is, distinct) C2 axes or σ planes 1 C5 axis coming out of the page - 2 H 5 H H H H 3 4 C734b Symmetry Operations and 17 Point groups * When > one symmetry axis exist, the one with the largest value of n ≡ PRINCIPLE AXIS Things are a bit more subtle for Cn, n even Take for example C4 axis: C2(1) 2 1 C2(2) 3 4 C734b Symmetry Operations and 18 Point groups 9 C2(2) 1 4 C4 C2(1) 2 3 i.e.; C2(1) → C2(2); C2(2) → C2(1) C2(1) 4 3 C4 C2(2) 2 Total = C4 = C2 i.e.; C2(1) → C2(1); C2(2) → C2(2) 1 2 C734b Symmetry Operations and 19 Point groups C2(1) 2 1 C4 C2(2) 3 -1 Total C4 = C4 3 4 i.e.; C2(1) → C2(2); C2(2) → C2(1) Conclusion: C2(1) and C2(2) are not distinct Conclusion: a Cn axis, n even, may be accompanied by n/2 sets of 2 C2 axes C734b Symmetry Operations and 20 Point groups 10 b 2 a2 b1 a1 4 C2 axes: (a1, a2) and (b1, b2). Cn rotational groups are Abelian C734b Symmetry Operations and 21 Point groups 4. Improper Axes and Improper Rotations Accurate definitions: Improper rotation is a proper rotation R(Φ, n) followed by inversion ≡ iR(Φ, n) Rotoreflection is a proper reflection R(Φ, n) followed by reflection in a plane normal to the axis of rotation, σh Called Sn = σhR(Φ, n) Φ = 2π/n Cotton and many other books for chemists call Sn an improper rotation, and we will too. C734b Symmetry Operations and 22 Point groups 11 Example: staggered ethane (C3 axis but no C6 axis) 1 4 1 2 3 2 σh 6 5 C 6 3 4 6 4 1 2 6 5 5 3 C734b Symmetry Operations and 23 Point groups Note: 1 4 6 4 3 2 C6 6 5 σ 6 h 5 6 1 4 1 2 3 2 5 3 S = σ C or C σ ⇒ n h n n h The order is irrelevant. C734b Symmetry Operations and 24 Point groups 12 Clear if Cn exists and σh exists Sn must exist. HOWEVER: Sn can exist if Cn and σh do not. The example above for staggered ethane is such a case. 2 3 The element Sn generates operations Sn, Sn , Sn , … However the set of operations generated are different depending if n is even or odd. n even {S , S 2, S 3, …, S n} 2 2 3 3 n n n n n n ≡ {σhCn, σh Cn , σh Cn , …, σh Cn } n But σ n = E and C n = E Sn = E h n ⇒ n+1 n+2 2 m m and therefore: Sn = Sn, Sn = Sn , etc, and Sn = Cn if m is even.
Load more

Recommended publications
  • Angle Chasing
    Angle Chasing Ray Li June 12, 2017 1 Facts you should know 1. Let ABC be a triangle and extend BC past C to D: Show that \ACD = \BAC + \ABC: 2. Let ABC be a triangle with \C = 90: Show that the circumcenter is the midpoint of AB: 3. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove that H is the incenter of 4DEF . 4. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove (i) that A; E; F; H lie on a circle diameter AH and (ii) that B; E; F; C lie on a circle with diameter BC. 5. Let ABC be a triangle with circumcenter O and orthocenter H: Show that \BAH = \CAO: 6. Let ABC be a triangle with circumcenter O and orthocenter H and let AH and AO meet the circumcircle at D and E, respectively. Show (i) that H and D are symmetric with respect to BC; and (ii) that H and E are symmetric with respect to the midpoint BC: 7. Let ABC be a triangle with altitudes AD; BE; and CF: Let M be the midpoint of side BC. Show that ME and MF are tangent to the circumcircle of AEF: 8. Let ABC be a triangle with incenter I, A-excenter Ia, and D the midpoint of arc BC not containing A on the circumcircle. Show that DI = DIa = DB = DC: 9. Let ABC be a triangle with incenter I and D the midpoint of arc BC not containing A on the circumcircle.
    [Show full text]
  • Proofs with Perpendicular Lines
    3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units.
    [Show full text]
  • Symmetry and Tensors Rotations and Tensors
    Symmetry and tensors Rotations and tensors A rotation of a 3-vector is accomplished by an orthogonal transformation. Represented as a matrix, A, we replace each vector, v, by a rotated vector, v0, given by multiplying by A, 0 v = Av In index notation, 0 X vm = Amnvn n Since a rotation must preserve lengths of vectors, we require 02 X 0 0 X 2 v = vmvm = vmvm = v m m Therefore, X X 0 0 vmvm = vmvm m m ! ! X X X = Amnvn Amkvk m n k ! X X = AmnAmk vnvk k;n m Since xn is arbitrary, this is true if and only if X AmnAmk = δnk m t which we can rewrite using the transpose, Amn = Anm, as X t AnmAmk = δnk m In matrix notation, this is t A A = I where I is the identity matrix. This is equivalent to At = A−1. Multi-index objects such as matrices, Mmn, or the Levi-Civita tensor, "ijk, have definite transformation properties under rotations. We call an object a (rotational) tensor if each index transforms in the same way as a vector. An object with no indices, that is, a function, does not transform at all and is called a scalar. 0 A matrix Mmn is a (second rank) tensor if and only if, when we rotate vectors v to v , its new components are given by 0 X Mmn = AmjAnkMjk jk This is what we expect if we imagine Mmn to be built out of vectors as Mmn = umvn, for example. In the same way, we see that the Levi-Civita tensor transforms as 0 X "ijk = AilAjmAkn"lmn lmn 1 Recall that "ijk, because it is totally antisymmetric, is completely determined by only one of its components, say, "123.
    [Show full text]
  • Properties of the Single and Double D4d Groups and Their Isomorphisms with D8 and C8v Groups A
    Properties of the single and double D4d groups and their isomorphisms with D8 and C8v groups A. Le Paillier-Malécot, L. Couture To cite this version: A. Le Paillier-Malécot, L. Couture. Properties of the single and double D4d groups and their isomorphisms with D8 and C8v groups. Journal de Physique, 1981, 42 (11), pp.1545-1552. 10.1051/jphys:0198100420110154500. jpa-00209347 HAL Id: jpa-00209347 https://hal.archives-ouvertes.fr/jpa-00209347 Submitted on 1 Jan 1981 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. J. Physique 42 (1981) 1545-1552 NOVEMBRE 1981, 1545 Classification Physics Abstracts 75.10D Properties of the single and double D4d groups and their isomorphisms with D8 and C8v groups A. Le Paillier-Malécot Laboratoire de Magnétisme et d’Optique des Solides, 1, place A.-Briand, 92190 Meudon Bellevue, France and Université de Paris-Sud XI, Centre d’Orsay, 91405 Orsay Cedex, France and L. Couture Laboratoire Aimé-Cotton (*), C.N.R.S., Campus d’Orsay, 91405 Orsay Cedex, France and Laboratoire d’Optique et de Spectroscopie Cristalline, Université Pierre-et-Marie-Curie, Paris VI, 75230 Paris Cedex 05, France (Reçu le 15 mai 1981, accepté le 9 juillet 1981) Résumé.
    [Show full text]
  • Molecular Symmetry
    Molecular Symmetry Symmetry helps us understand molecular structure, some chemical properties, and characteristics of physical properties (spectroscopy) – used with group theory to predict vibrational spectra for the identification of molecular shape, and as a tool for understanding electronic structure and bonding. Symmetrical : implies the species possesses a number of indistinguishable configurations. 1 Group Theory : mathematical treatment of symmetry. symmetry operation – an operation performed on an object which leaves it in a configuration that is indistinguishable from, and superimposable on, the original configuration. symmetry elements – the points, lines, or planes to which a symmetry operation is carried out. Element Operation Symbol Identity Identity E Symmetry plane Reflection in the plane σ Inversion center Inversion of a point x,y,z to -x,-y,-z i Proper axis Rotation by (360/n)° Cn 1. Rotation by (360/n)° Improper axis S 2. Reflection in plane perpendicular to rotation axis n Proper axes of rotation (C n) Rotation with respect to a line (axis of rotation). •Cn is a rotation of (360/n)°. •C2 = 180° rotation, C 3 = 120° rotation, C 4 = 90° rotation, C 5 = 72° rotation, C 6 = 60° rotation… •Each rotation brings you to an indistinguishable state from the original. However, rotation by 90° about the same axis does not give back the identical molecule. XeF 4 is square planar. Therefore H 2O does NOT possess It has four different C 2 axes. a C 4 symmetry axis. A C 4 axis out of the page is called the principle axis because it has the largest n . By convention, the principle axis is in the z-direction 2 3 Reflection through a planes of symmetry (mirror plane) If reflection of all parts of a molecule through a plane produced an indistinguishable configuration, the symmetry element is called a mirror plane or plane of symmetry .
    [Show full text]
  • Chapter 1 – Symmetry of Molecules – P. 1
    Chapter 1 – Symmetry of Molecules – p. 1 - 1. Symmetry of Molecules 1.1 Symmetry Elements · Symmetry operation: Operation that transforms a molecule to an equivalent position and orientation, i.e. after the operation every point of the molecule is coincident with an equivalent point. · Symmetry element: Geometrical entity (line, plane or point) which respect to which one or more symmetry operations can be carried out. In molecules there are only four types of symmetry elements or operations: · Mirror planes: reflection with respect to plane; notation: s · Center of inversion: inversion of all atom positions with respect to inversion center, notation i · Proper axis: Rotation by 2p/n with respect to the axis, notation Cn · Improper axis: Rotation by 2p/n with respect to the axis, followed by reflection with respect to plane, perpendicular to axis, notation Sn Formally, this classification can be further simplified by expressing the inversion i as an improper rotation S2 and the reflection s as an improper rotation S1. Thus, the only symmetry elements in molecules are Cn and Sn. Important: Successive execution of two symmetry operation corresponds to another symmetry operation of the molecule. In order to make this statement a general rule, we require one more symmetry operation, the identity E. (1.1: Symmetry elements in CH4, successive execution of symmetry operations) 1.2. Systematic classification by symmetry groups According to their inherent symmetry elements, molecules can be classified systematically in so called symmetry groups. We use the so-called Schönfliess notation to name the groups, Chapter 1 – Symmetry of Molecules – p. 2 - which is the usual notation for molecules.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
  • Symmetry of Graphs. Circles
    Symmetry of graphs. Circles Symmetry of graphs. Circles 1 / 10 Today we will be interested in reflection across the x-axis, reflection across the y-axis and reflection across the origin. Reflection across y reflection across x reflection across (0; 0) Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object. It is called symmetric if some geometric move preserves it Symmetry of graphs. Circles 2 / 10 Reflection across y reflection across x reflection across (0; 0) Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object. It is called symmetric if some geometric move preserves it Today we will be interested in reflection across the x-axis, reflection across the y-axis and reflection across the origin. Symmetry of graphs. Circles 2 / 10 Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object. It is called symmetric if some geometric move preserves it Today we will be interested in reflection across the x-axis, reflection across the y-axis and reflection across the origin. Reflection across y reflection across x reflection across (0; 0) Symmetry of graphs. Circles 2 / 10 Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object.
    [Show full text]
  • Symmetry in Chemistry
    SYMMETRY IN CHEMISTRY Professor MANOJ K. MISHRA CHEMISTRY DEPARTMENT IIT BOMBAY ACKNOWLEGDEMENT: Professor David A. Micha Professor F. A. Cotton 1 An introduction to symmetry analysis WHY SYMMETRY ? Hψ = Eψ For H – atom: Each member of the CSCO labels, For molecules: Symmetry operation R CSCO H is INVARIANT under R ( by definition too) 2 An introduction to symmetry analysis Hψ = Eψ gives NH3 normal modes = NH3 rotation or translation MUST be A1, A2 or E ! NO ESCAPING SYMMETRY! 3 Molecular Symmetry An introduction to symmetry analysis (Ref.: Inorganic chemistry by Shirver, Atkins & Longford, ELBS) One aspect of the shape of a molecule is its symmetry (we define technical meaning of this term in a moment) and the systematic treatment and symmetry uses group theory. This is a rich and powerful subject, by will confine our use of it at this stage to classifying molecules and draw some general conclusions about their properties. An introduction to symmetry analysis Our initial aim is to define the symmetry of molecules much more precisely than we have done so far, and to provide a notational scheme that confirms their symmetry. In subsequent chapters we extend the material present here to applications in bonding and spectroscopy, and it will become that symmetry analysis is one of the most pervasive techniques in inorganic chemistry. Symmetry operations and elements A fundamental concept of group theory is the symmetry operation. It is an action, such as a rotation through a certain angle, that leave molecules apparently unchanged. An example is the rotation of H2O molecule by 180 ° (but not any smaller angle) around the bisector of HOH angle.
    [Show full text]
  • Rotation Matrix - Wikipedia, the Free Encyclopedia Page 1 of 22
    Rotation matrix - Wikipedia, the free encyclopedia Page 1 of 22 Rotation matrix From Wikipedia, the free encyclopedia In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix rotates points in the xy -Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv (see below for details). In two and three dimensions, rotation matrices are among the simplest algebraic descriptions of rotations, and are used extensively for computations in geometry, physics, and computer graphics. Though most applications involve rotations in two or three dimensions, rotation matrices can be defined for n-dimensional space. Rotation matrices are always square, with real entries. Algebraically, a rotation matrix in n-dimensions is a n × n special orthogonal matrix, i.e. an orthogonal matrix whose determinant is 1: . The set of all rotation matrices forms a group, known as the rotation group or the special orthogonal group. It is a subset of the orthogonal group, which includes reflections and consists of all orthogonal matrices with determinant 1 or -1, and of the special linear group, which includes all volume-preserving transformations and consists of matrices with determinant 1. Contents 1 Rotations in two dimensions 1.1 Non-standard orientation
    [Show full text]
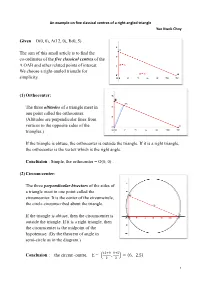
  • An Example on Five Classical Centres of a Right Angled Triangle
    An example on five classical centres of a right angled triangle Yue Kwok Choy Given O(0, 0), A(12, 0), B(0, 5) . The aim of this small article is to find the co-ordinates of the five classical centres of the ∆ OAB and other related points of interest. We choose a right-angled triangle for simplicity. (1) Orthocenter: The three altitudes of a triangle meet in one point called the orthocenter. (Altitudes are perpendicular lines from vertices to the opposite sides of the triangles.) If the triangle is obtuse, the orthocenter is outside the triangle. If it is a right triangle, the orthocenter is the vertex which is the right angle. Conclusion : Simple, the orthocenter = O(0, 0) . (2) Circum-center: The three perpendicular bisectors of the sides of a triangle meet in one point called the circumcenter. It is the center of the circumcircle, the circle circumscribed about the triangle. If the triangle is obtuse, then the circumcenter is outside the triangle. If it is a right triangle, then the circumcenter is the midpoint of the hypotenuse. (By the theorem of angle in semi-circle as in the diagram.) Conclusion : the circum -centre, E = ͥͦͮͤ ͤͮͩ ʠ ͦ , ͦ ʡ Ɣ ʚ6, 2.5ʛ 1 Exercise 1: (a) Check that the circum -circle above is given by: ͦ ͦ ͦ. ʚx Ǝ 6ʛ ƍ ʚy Ǝ 2.5ʛ Ɣ 6.5 (b) Show that t he area of the triangle with sides a, b, c and angles A, B, C is ΏΐΑ ͦ , where R is the radius of the circum -circle .
    [Show full text]