CS 173: Discrete Structures, Spring 2013 Homework 3 Solutions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Master Class with Andrea Martin: Selected Filmography 1 the Higher
Master Class with Andrea Martin: Selected Filmography The Higher Learning staff curate digital resource packages to complement and offer further context to the topics and themes discussed during the various Higher Learning events held at TIFF Bell Lightbox. These filmographies, bibliographies, and additional resources include works directly related to guest speakers’ work and careers, and provide additional inspirations and topics to consider; these materials are meant to serve as a jumping-off point for further research. Please refer to the event video to see how topics and themes relate to the Higher Learning event. Films and Television Series mentioned or discussed during the Master Class 8½. Dir. Federico Fellini, 1963, Italy and France. 138 mins. Production Co.: Cineriz / Francinex. American Dad! (2005-2012). 7 seasons, 133 episodes. Creators: Seth MacFarlane, Mike Barker, and Matt Weitzman. U.S.A. Originally aired on Fox. 20th Century Fox Television / Atlantic Creative / Fuzzy Door Productions / Underdog Productions. Auntie Mame. Dir. Morton DaCosta, 1958, U.S.A. 143 mins. Production Co.: Warner Bros. Pictures. Breaking Upwards. Dir. Daryl Wein, 2009, U.S.A. 88mins. Production Co.: Daryl Wein Films. Bridesmaids. Dir. Paul Feig, 2011, U.S.A. 125 mins. Production Co.: Universal Pictures / Relativity Media / Apatow Productions. Cannibal Girls. Dir. Ivan Reitman, 1973, Canada. 84 mins. Production Co.: Scary Pictures Productions. The Cleveland Show (2009-2012). 3 seasons, 65 episodes. Creators: Richard Appel, Seth MacFarlane, and Mike Henry. U.S.A. Originally aired on Fox. Production Co.: Persons Unknown Productions / Happy Jack Productions / Fuzzy Door Productions / 20th Century Fox Television. Club Paradise. Dir. Harold Ramis, 1986, U.S.A. -

Family Guy: TV’S Most Shocking Show Chapter Three 39 Macfarlane Steps in Front of the Camera
CONTENTS Introduction 6 Humor on the Edge Chapter One 10 Born to Cartoon Chapter Two 24 Family Guy: TV’s Most Shocking Show Chapter Three 39 MacFarlane Steps in Front of the Camera Chapter Four 52 Expanding His Fan Base Source Notes 66 Important Events in the Life of Seth MacFarlane 71 For Further Research 73 Index 75 Picture Credits 79 About the Author 80 MacFarlane_FamilyGuy_CCC_v4.indd 5 4/1/15 8:12 AM CHAPTER TWO Family Guy: TV’s Most Shocking Show eth MacFarlane spent months drawing images for the pilot at his Skitchen table, fi nally producing an eight-minute version of Fam- ily Guy for network broadcast. After seeing the brief pilot, Fox ex- ecutives green-lighted the series. Says Sandy Grushow, president of 20th Century Fox Television, “Th at the network ordered a series off of eight minutes of fi lm is just testimony to how powerful those eight minutes were. Th ere are very few people in their early 20’s who have ever created a television series.”20 Family Guy made its debut on network television on January 31, 1999—right after Fox’s telecast of the Super Bowl. Th e show import- ed the Life of Larry and Larry & Steve dynamic of a bumbling dog owner and his pet (renamed Peter Griffi n and Brian, respectively) and expanded the supporting family to include wife, Lois; older sis- ter, Meg; middle child, Chris; and baby, Stewie. Th e audience for the Family Guy debut was recorded at 22 million. Given the size of the audience, Fox believed MacFarlane had produced a hit and off ered him $1 million a year to continue production. -

2010 Annual Report
2010 ANNUAL REPORT Table of Contents Letter from the President & CEO ......................................................................................................................5 About The Paley Center for Media ................................................................................................................... 7 Board Lists Board of Trustees ........................................................................................................................................8 Los Angeles Board of Governors ................................................................................................................ 10 Media Council Board of Governors ..............................................................................................................12 Public Programs Media As Community Events ......................................................................................................................14 INSIDEMEDIA Events .................................................................................................................................14 PALEYDOCFEST ......................................................................................................................................20 PALEYFEST: Fall TV Preview Parties ...........................................................................................................21 PALEYFEST: William S. Paley Television Festival ......................................................................................... 22 Robert M. -

The Casting Director Guide from Now Casting, Inc
The Casting Director Guide From Now Casting, Inc. This printable Casting Director Guide includes CD listings exported from the CD Connection in NowCasting.com’s Contacts NOW area. The Guide is an easy way to get familiar with all the CD’s. Or, you might want to print a copy that lives in your car. Keep in mind that the printable CD Guide is created approximately once a month while the CD Connection is updated constantly. There will be info in the printable “Guide” that is out of date almost immediately… that’s the nature of casting. If you need a more comprehensive, timely and searchable research and marketing tool then you should consider using Contacts NOW in NowCasting.com. In Contacts NOW, you can search the CD database directly, make personal notes, create mailing lists, search Agents, make your own Custom Contacts and print labels. You can even export lists into Postcards NOW – a service that lets you create and mail postcards all from your desktop! You will find Contacts NOW in your main NowCasting menu under Get it NOW or Guides and Labels. Questions? Contact the NowCasting Staff @ 818-841-7165 Now Casting.com We’re Back! Many post hiatus updates! October ‘09 $13.00 Casting Director Guide Run BY Actors FOR Actors More UP- TO-THE-MINUTE information than ANY OTHER GUIDE Compare to the others with over 100 pages of information Got Casting Notices? We do! www.nowcasting.com WHY BUY THIS BOOK? Okay, there are other books on the market, so why should you buy this one? Simple. -
A&E 04 Mon 08-04-2014.Indd
4 Page 4 – Monday, August 4, 2014 SENTINEL-TRIBUNE AR T S & ENTERTAINMENT MONDAY EVENING AUGUST 4, 2014 Chan. 7:00 7:30 8:00 8:30 9:00 9:30 10:00 10:30 11:00 11:30 BROADCAST CHANNELS NBC Judge Judy Criminal Judge Judy A phone Running Wild With Bear Grylls “Ben Stiller” American Ninja Warrior “Denver Finals” The Denver finals course. (N) ‘PG’ (DVS) NBC 24 News (N) Å (11:34) The Tonight charges against a child. with text evidence goes Ben Stiller in Northern Scotland. (N) (In Stereo) Show Starring Jimmy 24 (In Stereo) Å missing. Å ‘PG’ Å Fallon (N) ‘14’ Å CBS Wheel of Fortune Jeopardy! “Teachers 2 Broke Girls Max de- Mom “Pilot” Christy’s Mike & Molly A trip to Two and a Half Men Under the Dome “In the Dark” Barbie and Sam WTOL 11 News at (11:35) Late Show With “Southern Hospitality” Tournament Week 2” (In cides to end things with estranged mother re- a riverboat casino. (In Walden helps Jenny investigate a tunnel. (N) (In Stereo) ‘14’ Å Eleven (N) (In Ste- David Letterman (N) 11 (In Stereo) ‘G’ Å Stereo) ‘G’ Å Deke. ‘14’ Å turns. ‘14’ Å Stereo) ‘14’ Å pursue acting. Å reo) Å (In Stereo) Å ABC Entertainment Tonight The Insider (N) (In Bachelor in Paradise (Series Premiere) Show veterans take another shot at love. (N) (In Stereo) (10:01) Mistresses “Coming Clean” Dom re- 13abc Action News at (11:35) Jimmy Kimmel (N) (In Stereo) Å Stereo) Å ‘14’ ceives news from Toni. -

Read Ebook {PDF EPUB} Double-Take Tales by Donna Brown Double-Take Tales by Donna Brown
Read Ebook {PDF EPUB} Double-take Tales by Donna Brown Double-take Tales by Donna Brown. Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. What can I do to prevent this in the future? If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. Cloudflare Ray ID: 661432ae1c85145a • Your IP : 116.202.236.252 • Performance & security by Cloudflare. ‘Not Aging At All!’: Tabitha Brown’s Throwback Picture Has Fans Demanding to Know Her Anti-Aging Secrets. Tabitha Brown and her husband Chance have been going strong for 17 years and are proof that when you’re happy in your marriage, time seems to almost come to a standstill. The 41-year-old vegan social media influencer and her entrepreneur hubby took a break from their weekly “Fridays with Tab & Chance” IGTV series to share a fly throwback image with their followers. In the five-year-old photo, the lovebirds are hugged up and all smiles. Tab’s printed leggings, fringe boots and tank were upstaged by her drastically different ‘do. The actress’ now-signature curly ‘fro, which she lovingly refers to as Donna, is straightened and dyed in the pic — a stark contrast to her dark brown color that fans are used to seeing. -

Seth Macfarlane Announced As Roast Master for the 'COMEDY CENTRAL Roast of Donald Trump'
Seth MacFarlane Announced as Roast Master for the 'COMEDY CENTRAL Roast Of Donald Trump' MacFarlane Becomes The First Roast Master In The Network's History To Host Consecutive "COMEDY CENTRAL Roasts" The "COMEDY CENTRAL Roast of Donald Trump" Tapes In New York City On Wednesday, March 9 And Premieres In Late March NEW YORK, Feb. 16, 2011 /PRNewswire via COMTEX/ -- COMEDY CENTRAL is raising the stakes and taking bets that the "COMEDY CENTRAL Roast of Donald Trump" will be the network's most extravagant, most elite and most explosive Roast yet. The network announced today that Emmy Award®-winning "Family Guy" creator, writer, voice-over actor and director Seth MacFarlane will regain his throne as COMEDY CENTRAL Roast Master as he takes on hosting duties for the "COMEDY CENTRAL Roast of Donald Trump." MacFarlane will become the first member of the crème-de-la-crème circle of COMEDY CENTRAL Roast Masters to emcee back-to-back network Roasts. His previous reign as Roast Master for the "COMEDY CENTRAL Roast Of David Hassellhoff" scored big with viewers - the special was the number one show in all of television with men 18-34. The "COMEDY CENTRAL Roast of Donald Trump" tapes at the Hammerstein Ballroom in New York City on Wednesday, March 9 and airs in late March on COMEDY CENTRAL. Roasters and attending talent will be announced shortly. The Emmy-Award®-nominated "COMEDY CENTRAL Roast" franchise returns to New York City for the first time since 2005. The previous Roasts taped in NYC were the "COMEDY CENTRAL Roast Of Denis Leary" and the top-rated Roast of all time, the "COMEDY CENTRAL Roast Of Jeff Foxworthy." The "COMEDY CENTRAL Roast Of Donald Trump" will be executive produced by Joel Gallen from Tenth Planet Productions, who was also executive producer and director of the following "COMEDY CENTRAL Roasts:" David Hasselhoff, Joan Rivers, Larry The Cable Guy, Bob Saget, Flavor-Flav, William Shatner (Emmy Award®-nominated) and Pamela Anderson. -

Family Guy. Which Isn’T a Criticism, Per Se
cover story By Josh Dean Photographs by Jill Greenberg Family Family Guy creator Seth MacFarlaneValues nabbed a record $100 million deal with Fox and is teaching Google new ways to exploit the Web. Could this crude frat-boy cartoonist really be a model for business in the modern age? November 2008 Fast company 99 toIt’s find not someone hard who delights in attacking the show Family Guy. Which isn’t a criticism, per se. Much of the and closing themes, and those, too, are when he writes a song, it’s going to be lush animated sitcom’s purpose seems to be to frequently updated, just because. Now, it and jazzy and, at least musically, exactly stoke the opposition, to offend the easily is not unprecedented to use a live orches- as you might hear it in something by offended. But that’s not the only reason it tra in today’s TV world. But it is highly Irving Berlin. It’s all part of a manic atten- annoys people. There is a school of thought unusual. “All the shows used to do it,” tion to detail that not only gives the show that says the show is hackish—crudely laments Walter Murphy, one of Family its layered humor but also has made Mac- drawn and derivative of its cartoon fore- Guy’s two composers. “It’s mostly elec- Farlane a massive, multiplatform success. bears. Members of this school would tronic now—to save money.” The Simpsons, But MacFarlane is more than just an include, most prominently, Ren & Stimpy he says, still uses an orchestra, as does eclectic entertainer. -

King of the Hill's Souphanousiphones, the New Model Minority, and the Subversive Model Minority
University of Mississippi eGrove Electronic Theses and Dissertations Graduate School 2012 King of the Hill's Souphanousiphones, the New Model Minority, and the Subversive Model Minority Robert Reece Follow this and additional works at: https://egrove.olemiss.edu/etd Part of the Sociology Commons Recommended Citation Reece, Robert, "King of the Hill's Souphanousiphones, the New Model Minority, and the Subversive Model Minority" (2012). Electronic Theses and Dissertations. 241. https://egrove.olemiss.edu/etd/241 This Dissertation is brought to you for free and open access by the Graduate School at eGrove. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of eGrove. For more information, please contact [email protected]. KING OF THE HILL’S SOUPHANOUSIPHONES, THE NEW MODEL MINORITY, AND THE SUBVERSIVE MODEL MINORITY A Thesis presented in partial fulfillment of requirements for the degree of Master of Arts in the Department of Sociology and Anthropology The University of Mississippi by ROBERT REECE May 2012 Copyright Robert Reece 2012 ALL RIGHTS RESERVED ABSTRACT Though the term “model minority” was only coined in the 1960s to apply to Asian- Americans, in the white imagination, a “model” way to be a minority has always existed. This model has gone through various iterations from the “happy” blacks of the antebellum years to supposedly over-achieving Asian-Americans of the 1960s. I argue that we are witnessing the emergence of a new model minority that includes not only Asian-Americans but other high- achieving minorities as well. This model minority is characterized by economic success, formal education, American values, and conservative racial politics or a complete silence about race. -
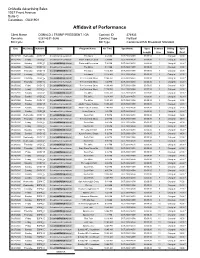
Affidavit of Performance
OnMedia Advertising Sales 1037 Front Avenue Suite C Columbus , GA31901 Affidavit of Performance Client Name DONALD J TRUMP PRESIDENT / GA Contract ID 274935 Remarks 62814631-3646 Contract Type Political Bill Cycle 9/20 Bill Type Condensed EAI Broadcast Standard Date Weekday Network Zone Program Name Air Time Spot Name Spot Contract Billing Spot Length Line Status Cost 09/23/2020 Wednesday CMDY_E Columbus-Valley-Auburn Futurama 8:43 AM DJT 20091405H 00:00:30 1 Charged 13.00 * 09/25/2020 Friday CMDY_E Columbus-Valley-AuburnWOW GA Parks and Recreation 7:39 AM DJT 20091405H 00:00:30 1 Charged 13.00 * 09/26/2020 Saturday CMDY_E Columbus-Valley-AuburnWOW GA Parks and Recreation 7:39 AM DJT 20091405H 00:00:30 1 Charged 13.00 * 09/26/2020 Saturday CMDY_E Columbus-Valley-AuburnWOW GA The Office 8:44 AM DJT 20091405H 00:00:30 1 Charged 13.00 * 09/24/2020 Thursday CMDY_E Columbus-Valley-AuburnWOW GA Futurama 11:12 AM DJT 20091405H 00:00:30 3 Charged 13.00 * 09/24/2020 Thursday CMDY_E Columbus-Valley-AuburnWOW GA Futurama 11:25 AM DJT 20091405H 00:00:30 3 Charged 13.00 * 09/24/2020 Thursday CMDY_E Columbus-Valley-AuburnWOW GA The Cleveland Show 11:46 AM DJT 20091405H 00:00:30 3 Charged 13.00 * 09/24/2020 Thursday CMDY_E Columbus-Valley-AuburnWOW GA The Cleveland Show 1:40 PM DJT 20091405H 00:00:30 3 Charged 13.00 * 09/25/2020 Friday CMDY_E Columbus-Valley-AuburnWOW GA The Cleveland Show 11:39 AM DJT 20091405H 00:00:30 3 Charged 13.00 * 09/25/2020 Friday CMDY_E Columbus-Valley-AuburnWOW GA The Cleveland Show 12:39 PM DJT 20091405H 00:00:30 3 Charged -

A Comparative Analysis of Promos During the Super Bowl for Fox and NBC Nathan R
Southern Illinois University Carbondale OpenSIUC Research Papers Graduate School 7-2012 A Comparative Analysis of Promos During the Super Bowl for Fox and NBC Nathan R. Mitchell [email protected] Follow this and additional works at: http://opensiuc.lib.siu.edu/gs_rp Recommended Citation Mitchell, Nathan R., "A Comparative Analysis of Promos During the Super Bowl for Fox and NBC" (2012). Research Papers. Paper 279. http://opensiuc.lib.siu.edu/gs_rp/279 This Article is brought to you for free and open access by the Graduate School at OpenSIUC. It has been accepted for inclusion in Research Papers by an authorized administrator of OpenSIUC. For more information, please contact [email protected]. A COMPARATIVE ANALYSIS OF PROMOS DURING THE SUPER BOWL FOR FOX AND NBC by Nathan R. Mitchell B.A., Southern Illinois University Carbondale, 2008 A Research Paper Submitted in Partial Fulfillment of the Requirements for the Master of Science Department of Mass Communications and Media Arts in the Graduate School Southern Illinois University Carbondale August 2012 RESERCH PAPER APPROVAL A COMPARATIVE ANALYSIS OF PROMOS DURING THE SUPER BOWL FOR FOX AND NBC by Nathan R. Mitchell A Research Paper Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in Mass Communications and Media Arts in the field of Professional Media & Media Management Approved by: Dr. Narayanan Iyer, Chair Graduate School Southern Illinois University Carbondale July 2012 AN ABSTRACT OF THE RESEARCH PAPER OF NATHAN R. MITCHELL, for the Master of Science degree in Professional Media and Media Management, presented on June 29, 2012, at Southern Illinois University Carbondale. -

The Association of Animated Sitcom Viewing with Humor Styles and Humor Types
HUMOR 2021; 34(3): 393–409 Ágnes Zsila*, Róbert Urbán, Gábor Orosz and Zsolt Demetrovics The association of animated sitcom viewing with humor styles and humor types https://doi.org/10.1515/humor-2020-0055 Received November 25, 2019; accepted August 27, 2020; published online February 9, 2021 Abstract: Recently, animated sitcoms such as Family Guy and American Dad have generated considerable interest internationally. This genre is known for its portrayal of controversial political and social issues combined with strategies of malicious humor, exaggeration, and stereotyping. This study addresses the ques- tion of whether humor styles and humor types predict viewer interest in animated sitcoms. A total of 1,052 Hungarian adults (41.6% male, Mage = 24.7 years, SD = 7.2) participated in an online survey focusing on animated sitcom viewing habits and the use of humor. It was found that males and younger individuals were more likely to watch animated sitcoms regularly than females and older individuals. As a result of multiple regressions, it was also found that individuals with high levels of self- enhancing and aggressive humor, and low levels of self-defeating humor were more likely to view animated sitcoms. Regarding humor types, individuals with low levels of all humor styles were less likely to watch animated sitcoms regularly. These findings can possibly contribute to a more nuanced understanding of media selection preferences in the level of individual differences. Keywords: animated sitcom; humor styles; humor types; media preferences;