Optimal Play of the Dice Game Pig Todd W
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Quizinfo Level
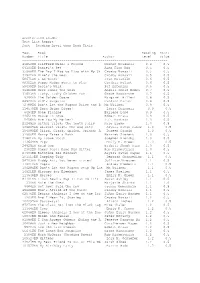
Accelerated Reader Test List Report Sort – Reading Level then Book Title Test Book Reading Point Number Title Author Level Value -------------------------------------------------------------------------- 41850EN Clifford Makes a Friend Norman Bridwell 0.4 0.5 64100EN Daniel's Pet Alma Flor Ada 0.5 0.5 35988EN The Day I Had to Play with My Si Crosby Bonsall 0.5 0.5 31542EN Mine's the Best Crosby Bonsall 0.5 0.5 58671EN I Am Water Jean Marzollo 0.6 0.5 88312EN Puppy Mudge Wants to Play Cynthia Rylant 0.6 0.5 59439EN Rosie's Walk Pat Hutchins 0.6 0.5 31610EN Here Comes the Snow Angela Shelf Medea 0.7 0.5 31613EN Itchy, Itchy Chicken Pox Grace Maccarone 0.7 0.5 9366EN The Golden Goose Margaret Hillert 0.8 0.5 84920EN Sid's Surprise Candace Carter 0.8 0.5 72788EN Don't Let the Pigeon Drive the B Mo Willems 0.9 0.5 114579EN Dora Helps Diego! Laura Driscoll 0.9 0.5 6494EN Gone Fishing Earlene Long 0.9 0.5 44651EN Mouse in Love Robert Kraus 0.9 0.5 5456EN Are You My Mother? P.D. Eastman 1.0 0.5 21245EN Arthur Tricks the Tooth Fairy Marc Brown 1.0 0.5 106265EN Biscuit Visits the Big City Alyssa Satin Capuc 1.0 0.5 104090EN Click, Clack, Splish, Splash: A Doreen Cronin 1.0 0.5 31600EN Harry Takes a Bath Harriet Ziefert 1.0 0.5 31601EN My Loose Tooth Stephen Krensky 1.0 0.5 113649EN Pigs Emily K. -

The Day Center
May 2017 The Day Center Mon Tue Wed Thu Fri 1 2 3 4 5 8:45 Trivia, Talk & Fun 9:30 Today’s Hx & News (LF)/Bell Choir w/ 9:30 Today’s Hx & News (LF)/Dominoes 9:30 Today’s Hx & News (LF)/IN2L: Chick- 8:45 Trivia, Talk & Fun 9:30 Today’s Hx & News (CL)/Bocce Ball Amy (MR)/Bowling (SR)/Pampering (AR) (MR)/Ladder Ball (SR)/Kitchen Craft w/ tionary (CL)/Faith & Devotions (AR)/Bean 9:30 Today’s Hx & News (LF)/5 de Mayo (SR)/Noticias en Espanol (LF)/Farkle (AR) 10:15 Art w/Sandie (AR)/IN2L: Hangman Courtney (K) Bag Toss (SR) Word Puzzles (MR)/Bell Choir w/Amy 10:15 “The Golden Girls” w/Jenny (LF)/Flip (CL)/Stretch Exercise (SR)/FPT: Havana (LF) 10:15 Music w/Carol F (AR)/Grump Out Day 10:15 Stretch & Strength (SR)/Theater Thurs.: (AR)/Corn Hole (SR) 10 (DR)/Knitting Gp. (AR)/Stretch & 11:00 Lawn Darts (SR)/Postcard Collections (MR)/How It’s Made w/ Kendra (LF)/Exercise Audrey Hepburn (CL)/Who/What Am I? 10:15 Word Challenge w/Julie (AR)/Battle Strength (SR)/Battle of the Sexes (MR) (MR)/Art w/Sandie (AR)/Name 10 (LS) (SR) (AR)/Apples to Apples (MR) of Puebla Disc. & Trivia (CL)/Exercise 11:00 Velcro Ball Target (SR)/Scrabble 11:45 Lunch: Sweet & Sour Meatballs 11:00 Family Talk (LS)/Frog Pond (MR)/Music 11:00 Theater Thurs.: Audrey Hepburn (CL)/ (SR)/Toss Up Dice (MR) (AR)/Sp: Daily Inspirations (MR)/IN2L: 12:45 Travelin’ Tunes (CL)/Classic Board w/Carol F (AR)/PRUNE Categories (SR) Orange Juice Disc. -

Activity Calendar Mukwonago Memory Care Home
January 2020 Activity Calendar Mukwonago Memory Care Home S U N M O N T U E W E D T H U F R I S A T All activities, program dates, Morning - Looking Good, Morning - Looking Good, Morning - Looking Good, 9AM - Hair and Nails 1 Chief Review, Morning 2 Daily Chronicles, Morning Daily Chronicles, Morning and times are subject to Stretch Stretch 3 Stretch 4 10AM - Movie Madness change due to spontaneity 2:15PM - BINGO w/ Esther 2:15PM - De-Deck the 2:15PM - De-Deck the 11AM - Daily Chronicles Sunroom Living Rooms and unpredictability. 2:15PM - Yahtzee 3:30PM - Social/Juice Break 3:30PM - Social/Juice 3:30PM - Social/Juice 3PM - Social/Juice Break Break Break 3:30PM - Sensory 6PM - Sing-a-Long 6PM - Jeopardy 6:30PM - Friday Night Flick 7PM - Lawrence Walk 9AM - Makeovers Morning - Looking Good, Morning - Looking Good, Morning - Looking Good, Morning - Looking Good, Morning - Looking Good, 9AM - Hair and Nails 5 9:15AM - Catholic 6 Daily Chronicles, Morning 7 Brain Teasers, Morning 8 Chief Review, Morning 9 Daily Chronicles, 10 Daily Chronicles, Morning 11 Services Stretch Stretch Stretch Morning Stretch Stretch 10AM - Movie Madness 2:15PM - Farkle: Dice 2:15PM - National Bird 2:15PM - BINGO w/ Esther 2PM - Sing-a-Long CT1 2:15PM - Would you 11AM - Daily Chronicles 2:15PM - Table Games Rather... Day: Bird Seed Ornaments 2:15PM - Scenic Drive 2:15PM - Yahtzee 3PM - Social/Juice Break 3:30PM - Social/Juice CT2 3PM - Social/Juice Break 3PM - Social 3:30PM - Volleyball 3:30PM - Social/Juice Break Break 3:30PM - Karaoke 3PM - Sensory 3:30PM - Reminisce -

New Yahtzee Game Cheats Magnoliasouth
new yahtzee game cheats MagnoliaSouth. Before I get to it, let me just say that despite what I say and complain about here, I still love the game, the author and the website. The games aren't something we have to download. They're not something we have to have an account for. They're not something that requires us to watch ads for. They are just the old fashioned games and that's that. For this reason alone, they're all worth playing. I give the author, Einar Egilsson, kudos for giving us these great games for free. I've played others, but this one is about the Yahtzee game. There are similarities in the other games, but those are for another post on another day. I just want to talk about this one today. Normally I'm an option girl. I want options. I want to be able to choose single player vs. other players. I want to customize my cards and backgrounds and so on. These are plain and options are limited. I'm okay with that. They're clean, free and ad free. For this reason plain is good here. There is just one problem, probability. The author insists that it is not written to favor the computer and maybe it isn't. Only thing is, it does favor the computer and I kind of have the proof. Let me show you. Update #2: Take a look at this one, the same game a few rolls later. As soon as I got the bonus, look who got ANOTHER Yahtzee. -

February 2017 the Day Center
February 2017 The Day Center Mon Tue Wed Thu Fri 1 2 3 9:30 Today’s Hx & News (LF)/Cow Patty 9:30 Today’s Hx & News (LF)/Prayer Circle 8:45 Trivia, Talk & Fun Chucking (SR)/Bell Choir w/Joan (MR)/Pass (AR)/Weights Exercise (SR)/Spring or Snow? 9:30 Today’s News & Hx (LF)/LUMPS the Pigs (AR) (MR) Dice (MR)/Bell Choir w/Amy (AR)/Corn 10:15 Art w/Sandie (AR)/February IQ (MR)/ 10:15 Pine Cone Toss (SR)/Groundhog Day Hole (SR) Noodle Exercise (SR)/FPT: Portland, OR (LF) Disc. (AR)/February BINGO (LD)/IN2L: 10:15 Word Challenge w/Julie (AR)/ 11:00 20 Questions (LS)/How It’s Made w/ Geography Games (CL) National Doodle Day (MR)/Exercise (SR)/ Kendra S (CL)/Art w/Sandie (AR)/Golf Putting 11:00 Book Club w/Amy (LS)/Outburst (AR)/ IN2L: Cat Fun (CL) (SR) Darts (SR)/I Hear Memories (MR) 11:00 HEART Categories (AR)/I Hear 11:45 Lunch: Stuffed Chicken & Rice Pilaf 11:45 Lunch: Hamburger & Baked Beans Memories (MR)/Historias en Espanol w/Elsa 12:45 Book Club w/Ann (MR)/Concentration 12:45 Mystery Birthday (AR)/Movie: Ground- (LS)/Dutch Shuffleboard (SR) (LD)/Ring Toss (SR)/IN2L: Farming Videos hog Day (LF)/Bowling (SR)/Music w/Carol F 11:45 Lunch: Citrus Salmon & Rice (CL) (MR) 12:45 Ribbon Exercise (MR)/Country Gos- 1:30 The Science of Finger Prints (MR)/Tenzies 1:30 Stretch & Strength (SR)/Movie: Ground- pel w/Bruce S (SR)/Book Club w/Ila (LS) (LD)/Spiritual Discussion w/Joan (AR)/Exercise hog Day (LF)/Music w/Carol F (MR)/ 1:30 Lawn Darts (MR)/Country Gospel w/ (SR) FEBRUARY Categories (AR) Bruce S (SR)/Prayer Circle (LD) 2:15 Hat Bingo (LD)/Balloon -

Rules of Play - Game Design Fundamentals
Table of Contents Table of Contents Table of Contents Rules of Play - Game Design Fundamentals.....................................................................................................1 Foreword..............................................................................................................................................................1 Preface..................................................................................................................................................................1 Chapter 1: What Is This Book About?............................................................................................................1 Overview.................................................................................................................................................1 Establishing a Critical Discourse............................................................................................................2 Ways of Looking.....................................................................................................................................3 Game Design Schemas...........................................................................................................................4 Game Design Fundamentals...................................................................................................................5 Further Readings.....................................................................................................................................6 -

A Couverture AFTER
UNIVERISTE D’ANTANANARIVO DEPARTEMENT DE FORMATION INITIAL LITERAIRE CENTRE D’ETUDE ET DE RECHERCHE EN LANGUE ET LETTRES ANGLAISES Using Snakes And Ladders Board Games With Dice to Teach Wishes and Regrets to Malagasy Students C.A.P.E.N. Dissertation Presented by TOMARIELSON Christian Espérant Advisor: RANDRIAMAMPIONONA Christiane ACADEMIC YEAR: 2014-2015 12 January 2016 Acknowledgments We would like to express our deepest gratitude to God for His guidance and everything He has done to me. First of all, we are extremely grateful to Mrs RANDRIAMAMPIONONA Christiane, our Dissertation Advisor for her invaluable kindness, patience, directives, encouragement, and keen editorial eye before the printing of the work. Our warmest thanks must equally go to Mr MANORO Regis and Mrs RAMINOARIVONY Mirany whose helpful comments and suggestions have helped us in the completion and the official presentation of our work. We would like to express our sincere acknowledgments to all teachers at the CER Langue et Lettres Anglaises, and we equally thank all those who contributed, in one way or another, to the elaboration of the present work. Last but by no means least, we wish to express our sincere gratitude to my wife, my children, and our friends who have supported us through their prayers, care, and encouragements. I TABLE OF CONTENTS GENERAL INTRODUCTION 0.1. Rationale and objective of the study 0.2.Scope and limitations 0.3. Structure of the work Part 1: THEORETICAL CONSIDERATIONS 1.1. On conditionals 1.1.1. Definitions of conditional construction……………………………………….........1 1.1.2. Likely conditionals……………………………………………………………........2 1.1.3. Unlikely conditionals…………………………………………………………........2 1.1.4. -

About Cards, Boards & Dice
Cards, Boards & Dice Hundreds of different Card Games, Board Games and Dice Games to play in solitude, against computer opponents and even against human players across the internet… Say goodbye to your spare time, and not so spare time ;) Disc 1 Disc 2 ♜ 3D Crazy Eights ♜ 3D Bridge Deluxe ♜ Mike's Marbles ♜ 3D Euchre Deluxe ♜ 3D Hearts Deluxe ♜ Mnemoni X ♜ 3D Spades Deluxe ♜ 5 Realms ♜ Monopoly Here & Now ♜ Absolute Farkle ♜ A Farewell to Kings ♜ NingPo Mahjong ♜ Aki Mahjong Solitaire ♜ Ancient Tripeaks 2 ♜ Pairs ♜ Ancient Hearts Spades ♜ Big Bang Board Games ♜ Patience X ♜ Bejeweled 2 ♜ Burning Monkey Mahjong ♜ Poker Dice ♜ Big Bang Brain Games ♜ Classic Sol ♜ Professor Code ♜ Boka Battleships ♜ CrossCards ♜ Sigma Chess ♜ Burning Monkey Solitaire ♜ Dominoes ♜ SkalMac Yatzy ♜ Cintos ♜ Free Solitaire 3D ♜ Snood Solitaire ♜ David's Backgammon ♜ Freecell ♜ Snoodoku ♜ Hardwood Solitaire III ♜ GameHouse Solitaire ♜ Solitaire Epic ♜ Jeopardy Deluxe Challenge ♜ Solitaire Plus ♜ Mah Jong Quest ♜ iDice ♜ Solitaire Till Dawn X ♜ Monopoly Classic ♜ iHearts ♜ Wiz Solitaire ♜ Neuronyx ♜ Kitty Spangles Solitaire ♜ ♜ Klondike The applications supplied on this CD are One Card s u p p l i e d a s i s a n d w e m a k e n o ♜ Rainbow Mystery ♜ Lux representations regarding the applications nor any information related thereto. Any ♜ Rainbow Web ♜ MacPips Jigsaw questions, complaints or claims regarding the ♜ applications must be directed to the ♜ Scrabble MacSudoku appropriate software vendor. ♜ ♜ Simple Yahtzee X MahJong Medley Various different license -

Authorized Catalogs - United States
Authorized Catalogs - United States Miché-Whiting, Danielle Emma "C" Vic Music @Canvas Music +2DB 1 Of 4 Prod. 10 Free Trees Music 10 Free Trees Music (Admin. by Word Music Group, 1000 lbs of People Publishing 1000 Pushups, LLC Inc obo WB Music Corp) 10000 Fathers 10000 Fathers 10000 Fathers SESAC Designee 10000 MINUTES 1012 Rosedale Music 10KF Publishing 11! Music 12 Gate Recordings LLC 121 Music 121 Music 12Stone Worship 1600 Publishing 17th Avenue Music 19 Entertainment 19 Tunes 1978 Music 1978 Music 1DA Music 2 Acre Lot 2 Dada Music 2 Hour Songs 2 Letit Music 2 Right Feet 2035 Music 21 Cent Hymns 21 DAYS 21 Songs 216 Music 220 Digital Music 2218 Music 24 Fret 243 Music 247 Worship Music 24DLB Publishing 27:4 Worship Publishing 288 Music 29:11 Church Productions 29:Eleven Music 2GZ Publishing 2Klean Music 2nd Law Music 2nd Law Music 2PM Music 2Surrender 2Surrender 2Ten 3 Leaves 3 Little Bugs 360 Music Works 365 Worship Resources 3JCord Music 3RD WAVE MUSIC 4 Heartstrings Music 40 Psalms Music 442 Music 4468 Productions 45 Degrees Music 4552 Entertainment Street 48 Flex 4th Son Music 4th teepee on the right music 5 Acre Publishing 50 Miles 50 States Music 586Beats 59 Cadillac Music 603 Publishing 66 Ford Songs 68 Guns 68 Guns 6th Generation Music 716 Music Publishing 7189 Music Publishing 7Core Publishing 7FT Songs 814 Stops Today 814 Stops Today 814 Today Publishing 815 Stops Today 816 Stops Today 817 Stops Today 818 Stops Today 819 Stops Today 833 Songs 84Media 88 Key Flow Music 9t One Songs A & C Black (Publishers) Ltd A Beautiful Liturgy Music A Few Good Tunes A J Not Y Publishing A Little Good News Music A Little More Good News Music A Mighty Poythress A New Song For A New Day Music A New Test Catalog A Pirates Life For Me Music A Popular Muse A Sofa And A Chair Music A Thousand Hills Music, LLC A&A Production Studios A. -

Finding Aid to the Sid Sackson Collection, 1867-2003
Brian Sutton-Smith Library and Archives of Play Sid Sackson Collection Finding Aid to the Sid Sackson Collection, 1867-2003 Summary Information Title: Sid Sackson collection Creator: Sid Sackson (primary) ID: 2016.sackson Date: 1867-2003 (inclusive); 1960-1995 (bulk) Extent: 36 linear feet Language: The materials in this collection are primarily in English. There are some instances of additional languages, including German, French, Dutch, Italian, and Spanish; these are denoted in the Contents List section of this finding aid. Abstract: The Sid Sackson collection is a compilation of diaries, correspondence, notes, game descriptions, and publications created or used by Sid Sackson during his lengthy career in the toy and game industry. The bulk of the materials are from between 1960 and 1995. Repository: Brian Sutton-Smith Library and Archives of Play at The Strong One Manhattan Square Rochester, New York 14607 585.263.2700 [email protected] Administrative Information Conditions Governing Use: This collection is open to research use by staff of The Strong and by users of its library and archives. Intellectual property rights to the donated materials are held by the Sackson heirs or assignees. Anyone who would like to develop and publish a game using the ideas found in the papers should contact Ms. Dale Friedman (624 Birch Avenue, River Vale, New Jersey, 07675) for permission. Custodial History: The Strong received the Sid Sackson collection in three separate donations: the first (Object ID 106.604) from Dale Friedman, Sid Sackson’s daughter, in May 2006; the second (Object ID 106.1637) from the Association of Game and Puzzle Collectors (AGPC) in August 2006; and the third (Object ID 115.2647) from Phil and Dale Friedman in October 2015. -

Dice Games Dice Games for Kids and for Kids and Families Families
FARKLE aside and throw the remaining dice. If they earn points you can combine the points with the points Number of Players: 2 or more from the first roll, but if you make a Farkle you lose all your points. Also the one from the first roll. You Age Range: 6 years and older are not allowed to combine the dice from the different rolls. Materials: 6 dice and pen and paper to keep score o The final round starts when one of the players has How to Play: more than 10,000 points. o The goal of this game is to be the first to reach 10,000 points or more Scoring o The first player starts rolling all six dice at the same For every 1 : 100 points time. For every 5 : 50 points o Points are earned when you roll a 1, 5, three of a kind, Three of a kind (all 1): 1000 points three pairs, a six dice straight (1,2,3,4,5,6), or two Three of a kind (all 2): 200 points triplets. See the score sheet below. Three of a kind (all 3): 300 points Three of a kind (all 4): 400 points o If none of the dice earned points you have made a Three of a kind (all 5): 500 points Farkle. The turn ends and the next player throws all Three of a kind (all 6): 600 points six dice. Straight six (1,2,3,4,5,6): 1500 points Three pair: 500 points o If you rolled one or more dice who earned points you Two triplets: 2500 points can chose to bank your points and give the dice to the Three Farkles in a row: LOSE 1000 points next player or continue with the other dice. -

Primary & Secondary Sources
Primary & Secondary Sources Brands & Products Agencies & Clients Media & Content Influencers & Licensees Organizations & Associations Government & Education Research & Data Multicultural Media Forecast 2019: Primary & Secondary Sources COPYRIGHT U.S. Multicultural Media Forecast 2019 Exclusive market research & strategic intelligence from PQ Media – Intelligent data for smarter business decisions In partnership with the Alliance for Inclusive and Multicultural Marketing at the Association of National Advertisers Co-authored at PQM by: Patrick Quinn – President & CEO Leo Kivijarv, PhD – EVP & Research Director Editorial Support at AIMM by: Bill Duggan – Group Executive Vice President, ANA Claudine Waite – Director, Content Marketing, Committees & Conferences, ANA Carlos Santiago – President & Chief Strategist, Santiago Solutions Group Except by express prior written permission from PQ Media LLC or the Association of National Advertisers, no part of this work may be copied or publicly distributed, displayed or disseminated by any means of publication or communication now known or developed hereafter, including in or by any: (i) directory or compilation or other printed publication; (ii) information storage or retrieval system; (iii) electronic device, including any analog or digital visual or audiovisual device or product. PQ Media and the Alliance for Inclusive and Multicultural Marketing at the Association of National Advertisers will protect and defend their copyright and all their other rights in this publication, including under the laws of copyright, misappropriation, trade secrets and unfair competition. All information and data contained in this report is obtained by PQ Media from sources that PQ Media believes to be accurate and reliable. However, errors and omissions in this report may result from human error and malfunctions in electronic conversion and transmission of textual and numeric data.