DOCSLIB.ORG

CPY Document

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CPY Document Linear and Multilinear Algebra, 1990, Vol. 28, pp. 3-33 Reprints available directly from the publisher Photocopying permitted by license only C9 199 Gordon and Breach Science Publishers S.A, Printed in the United States of America The Largest Eigenvalue of a Graph: A Survey i\ ~ D. CVETKOVIC Department of Mathematics, Faculty of Electrical Engineering, University of Belgrade, PO Box 816, 11001 Beograd, Yugoslavia P. ROWLINSON Department of Mathematics, University of Stirling, Stirling FK9 4LA, Scotland (Received March 1, 1990) Ths article is a survey of results concerning the largest eigenvalue (or index) of a graph, categorized as follows: (i) inequalities for the index, (2) graphs with bounded index, (3) ordering graphs by their indices, (4) graph operations and modifications, (5) random graphs, (6) applications, INTRODUCTION Almost all results related to the theory of graph spectra and published before 1984 are summarized in the monographs (27) and (28). In view of the rapid growth of the subject in subsequent years it is no longer reasonable to expect a single book to provide a comprehensive survey of the latest results. Instead it seems more ap- propriate that expository articles should be devoted to specific topics. For example the paper (68) reflects the recent realization that many results from analytic proba- bility theory have implications for the spectra of infinite graphs. Here we survey what is known about the largest eigenvalue of a finite graph. This topic embraces early results which go back to the very beginnings of the theory of graph spectra, together with recent developments concerning ordering and pertur- bations of graphs. Proofs which appear in (27) and (28) are not repeated here. We discuss only finite undirected graphs without loops or multiple edges, and we start with some basic definitions. Let G be a graph with n vertices, and let A be a (0,1)- adjacency matrix of G, regarded as a matrix with real entries. Since A is symmetric, its eigenvalues Ài, Ài,. .., Àn are real, and we assume that Ài ~ Ài ~ .. ~ Àn. These eigenvalues are independent of the ordering of the vertices of G, and accordingly we write Ài(G) = Ài(A) = Ài (i = i,...,n) and refer to Ài,....,ÀIi as the spectrum of G. The largest eigenvalue Ài is called the index of G (orl spectral radius of A). We call det(xI - A) the characteristic polynomial of G, denoted by ltG(x). The distinct eigenvalues of G wil be denoted by lli,..., llm, ordered as required. Since A is a non-negative matrix, some general information on the spectrum of G is provided by the Perron-Frobenius theory of matrices (45, 49, 57, 65, 67). In particular, if G is connected then A is irreducible and so there exists a unique positive unit eigen- vector corresponding to the index Ài. This vector we call the principal eigenvector of G: note that entries corresponding to vertices in the same orbit of Aut( G) are 3 LARGEST EIGENVALUE OF A GRAPH 5 4 D. CVETKOVlC AND P. ROWLINSON Let A denote the adjacency matrix of an n-vertex graph G. For any non-zero equal. We shall also use implicitly the fact that if G' is obtained from G by adding vector vE W the Rayleigh quotient vTAv/vTv is a lower bound for À1(G), as can an edge then À1(G') ~ À1(G), with strict inequality when G is connected: this is an be seen by diagonalizing A. If we take v to be the all-1 vector j then we obtain the immediate consequence of the fact that the spectral radius of a non-negative matrix inequality d ~ À1 of Theorem 1.1. Similarly, IAvl/lvl is a lower bound for À1, and increases with each entry. Further fundamental results in matrix theory which serve the next two results may be obtained by setting v = j, v = ei respectively, where the as a background to problems concerning the largest eigenvalue may be found in , i-th vertex of G has maxmal degree and ei = (6ii,...,6inl. (19, 35). We note in passing that although the eigenvalues of a directed multigraph need not be real, such a digraph has a positive eigenvalue À1 such that IÀI ~ À1 for THEOREM 1.2 (Hofmeister (54)) If the vertices of G have degrees d1,d2,.. .,dn then all eigenvalues À. Some results on the spectral radius of digraphs may be found in À1(G) ~ l(lln) ,,7=1 dr. (6, 83, 93, 98). For differing approaches to the spectra of infinite graphs, with some results on the largest eigenvalue, the reader is referred to Chapter VI of the mono- THEOREM 1. (Nosal (70); Lovász & Pelikán (62)) If dmax is the maxmal degree of graph (27), the expository article (68) and the paper (17). For the index in particular, a vertex in G then À1(G) ~ ldmax. see (8). The paper (96) extends to infinite graphs a result on finite graphs whose in- dex does not exceed V2 + v' (Theorem 2.4). Some discussion of the index of a Hofmeister went on to show that for any graph G, there exists a real number p, graph may be found in the expository papers (84, 91, 101). unique if G is non-regular, such that À1 (G) = \! (11 n) ,,7=1 dl. Finally we point out that several of the authors' results mentioned in this article Theorems 1.1 and 1.3 show that the index of a graph is controlled by the maxmal were conjectured on the basis of numerical evidence furnished by the expert system degree in the sense that À1 is bounded above and below by a function of dmax. Hoff- "Graph" (22, 23, 31, 90). In some instances, proofs were completed by using the man (51) observes that Ramsey-type arguments may be used to prove that À1(G) is system to check outstanding cases. controlled by the least number t such that neither Kt nor the star K1,t is an induced subgraph of G. We state one more result which demonstrates the interplay between index and 1. BOUNDS FOR THE INDEX OF A GRAPH vertex degrees. In a regular graph G of degree r on n vertices the number Nk Here we give upper and lower bounds for the index of a graph which are ex- of walks of length k is given by Nk = nrk; thus N Nk I n = r and this suggests that pressed in terms of various graph invariants. These bounds are interpreted and used N Nk I n in the general case might be regarded as a certain kind of mean value from different viewpoints in other sections of this article: in Section 2 for example of vertex degrees. Accordingly d = limk~+oo NNkln is defined to be the dynamic we survey classes of graphs defined by some bounds on the index. The discussion mean of the vertex degrees of an arbitrary graph G. of graph ordering in Section 3 and of graph perturbations in Section 4 is often con- the vertex cerned with bounds on the index. In §6.1 we return to the question of bounding THEOREM 1.4 (D. Cvetkovic (20)) For any graph G, the dynamic m~an of other graph invariants in terms of the index. degrees is equal to the index of G. In the fundamental paper (18) on the theory of graph spectra, Collatz and Sino- We give next some inequalities for the index of a graph involving the number n gowitz observed that the index À1 of a connected graph on n vertices satisfies the of vertices and the number e of edges. A part of Theorem 1.1 may be stated in inequality the form À1 ~ 2e I n, since 2e I n is the mean degree. An upper bound in terms of e 11 2cos-n+1 .: À1'':- - n - 1. and n may be obtained by maxmizing À1 subject only to the constraints ,,7=1 Ài = o and ,,7=1 ÀT = 2e (that is, tr(A) = 0 and tr(A2) = ,,7=1 di). Then we obtain the the The lower bound is attained by the path Pn while the upper bound is attained by following result of Wilf. complete graph Kn. If we omit the assumption of connectedness, then for a graph without edges we have À1 = 0 and otherwise À1 ~ 1. THEOREM 1.5 (100) For any graph G, À1(G) ~ V2e(1-1In). A reformulation of inequalities from the theory of non-negative matrices (67, The inequality in the next result was announced by Schwenk in (82), and a proof Chapter 2) yields the following theorem. by Yuan appeared some thirteen years later. THEOREM 1.1 Let dmim d, dmax respectively be the minimal, mean and maxmal val- THEOREM 1.6 (103) For any connected graph G, À1(G) ~ v2e - n + 1. Equality ues of the vertex degrees in a connected graph G. If À1 is the index of G then holds if and only if G is the star K1,n-1 or the complete graph Kn. dmin ~ d ~ À1 ~ dma. Proof Suppose that G has vertices 1,2,..., n and adjacency matrix A. Let di de- note the degree of vertex i and let Ci be the i-th column of A. Let x be the principal Equality in one place implies equality throughout; and this occurs if and only if G is eigenvector of A, say x = (xi,...,Xn)T, and let Vi be the vector whose j-th entry is reguar. LARGEST EIGENVALUE OF A GRAPH 7 6 D. CVETKOviC AND P.
Load more

Recommended publications
  • Two-Graphs and Skew Two-Graphs in Finite Geometries
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Two-Graphs and Skew Two-Graphs in Finite Geometries G. Eric Moorhouse Department of Mathematics University of Wyoming Laramie Wyoming Dedicated to Professor J. J. Seidel Submitted by Aart Blokhuis ABSTRACT We describe the use of two-graphs and skew (oriented) two-graphs as isomor- phism invariants for translation planes and m-systems (including avoids and spreads) of polar spaces in odd characteristic. 1. INTRODUCTION Two-graphs were first introduced by G. Higman, as natural objects for the action of certain sporadic simple groups. They have since been studied extensively by Seidel, Taylor, and others, in relation to equiangular lines, strongly regular graphs, and other notions; see [26]-[28]. The analogous oriented two-graphs (which we call skew two-graphs) were introduced by Cameron [7], and there is some literature on the equivalent notion of switching classes of tournaments. Our exposition focuses on the use of two-graphs and skew two-graphs as isomorphism invariants of translation planes, and caps, avoids, and spreads of polar spaces in odd characteristic. The earliest precedent for using two-graphs to study ovoids and caps is apparently owing to Shult [29]. The degree sequences of these two-graphs and skew two-graphs yield the invariants known as fingerprints, introduced by J. H. Conway (see Chames [9, lo]). Two LZNEAR ALGEBRA AND ITS APPLZCATZONS 226-228:529-551 (1995) 0 Elsevier Science Inc., 1995 0024-3795/95/$9.50 655 Avenue of the Americas, New York, NY 10010 SSDI 0024-3795(95)00242-J 530 G.
    [Show full text]
  • Hadamard and Conference Matrices
    Hadamard and conference matrices Peter J. Cameron December 2011 with input from Dennis Lin, Will Orrick and Gordon Royle Now det(H) is equal to the volume of the n-dimensional parallelepiped spanned by the rows of H. By assumption, each row has Euclidean length at most n1/2, so that det(H) ≤ nn/2; equality holds if and only if I every entry of H is ±1; > I the rows of H are orthogonal, that is, HH = nI. A matrix attaining the bound is a Hadamard matrix. Hadamard's theorem Let H be an n × n matrix, all of whose entries are at most 1 in modulus. How large can det(H) be? A matrix attaining the bound is a Hadamard matrix. Hadamard's theorem Let H be an n × n matrix, all of whose entries are at most 1 in modulus. How large can det(H) be? Now det(H) is equal to the volume of the n-dimensional parallelepiped spanned by the rows of H. By assumption, each row has Euclidean length at most n1/2, so that det(H) ≤ nn/2; equality holds if and only if I every entry of H is ±1; > I the rows of H are orthogonal, that is, HH = nI. Hadamard's theorem Let H be an n × n matrix, all of whose entries are at most 1 in modulus. How large can det(H) be? Now det(H) is equal to the volume of the n-dimensional parallelepiped spanned by the rows of H. By assumption, each row has Euclidean length at most n1/2, so that det(H) ≤ nn/2; equality holds if and only if I every entry of H is ±1; > I the rows of H are orthogonal, that is, HH = nI.
    [Show full text]
  • On Sign-Symmetric Signed Graphs∗
    ISSN 1855-3966 (printed edn.), ISSN 1855-3974 (electronic edn.) ARS MATHEMATICA CONTEMPORANEA 19 (2020) 83–93 https://doi.org/10.26493/1855-3974.2161.f55 (Also available at http://amc-journal.eu) On sign-symmetric signed graphs∗ Ebrahim Ghorbani Department of Mathematics, K. N. Toosi University of Technology, P.O. Box 16765-3381, Tehran, Iran Willem H. Haemers Department of Econometrics and Operations Research, Tilburg University, Tilburg, The Netherlands Hamid Reza Maimani , Leila Parsaei Majd y Mathematics Section, Department of Basic Sciences, Shahid Rajaee Teacher Training University, P.O. Box 16785-163, Tehran, Iran Received 24 October 2019, accepted 27 March 2020, published online 10 November 2020 Abstract A signed graph is said to be sign-symmetric if it is switching isomorphic to its negation. Bipartite signed graphs are trivially sign-symmetric. We give new constructions of non- bipartite sign-symmetric signed graphs. Sign-symmetric signed graphs have a symmetric spectrum but not the other way around. We present constructions of signed graphs with symmetric spectra which are not sign-symmetric. This, in particular answers a problem posed by Belardo, Cioaba,˘ Koolen, and Wang in 2018. Keywords: Signed graph, spectrum. Math. Subj. Class. (2020): 05C22, 05C50 1 Introduction Let G be a graph with vertex set V and edge set E. All graphs considered in this paper are undirected, finite, and simple (without loops or multiple edges). A signed graph is a graph in which every edge has been declared positive or negative. In fact, a signed graph Γ is a pair (G; σ), where G = (V; E) is a graph, called the underlying ∗The authors would like to thank the anonymous referees for their helpful comments and suggestions.
    [Show full text]
  • Pretty Good State Transfer in Discrete-Time Quantum Walks
    Pretty good state transfer in discrete-time quantum walks Ada Chan and Hanmeng Zhan Department of Mathematics and Statistics, York University, Toronto, ON, Canada fssachan, [email protected] Abstract We establish the theory for pretty good state transfer in discrete- time quantum walks. For a class of walks, we show that pretty good state transfer is characterized by the spectrum of certain Hermitian adjacency matrix of the graph; more specifically, the vertices involved in pretty good state transfer must be m-strongly cospectral relative to this matrix, and the arccosines of its eigenvalues must satisfy some number theoretic conditions. Using normalized adjacency matrices, cyclic covers, and the theory on linear relations between geodetic an- gles, we construct several infinite families of walks that exhibits this phenomenon. 1 Introduction arXiv:2105.03762v1 [math.CO] 8 May 2021 A quantum walk with nice transport properties is desirable in quantum com- putation. For example, Grover's search algorithm [12] is a quantum walk on the looped complete graph, which sends the all-ones vector to a vector that almost \concentrate on" a vertex. In this paper, we study a slightly stronger notion of state transfer, where the target state can be approximated with arbitrary precision. This is called pretty good state transfer. Pretty good state transfer has been extensively studied in continuous-time quantum walks, especially on the paths [9, 22, 1, 5, 21]. However, not much 1 is known for the discrete-time analogues. The biggest difference between these two models is that in a continuous-time quantum walk, the evolution is completely determined by the adjacency or Laplacian matrix of the graph, while in a discrete-time quantum walk, the transition matrix depends on more than just the graph - usually, it is a product of two unitary matrices: U = SC; where S permutes the arcs of the graph, and C, called the coin matrix, send each arc to a linear combination of the outgoing arcs of the same vertex.
    [Show full text]
  • Hadamard Matrices Include
    Hadamard and conference matrices Peter J. Cameron University of St Andrews & Queen Mary University of London Mathematics Study Group with input from Rosemary Bailey, Katarzyna Filipiak, Joachim Kunert, Dennis Lin, Augustyn Markiewicz, Will Orrick, Gordon Royle and many happy returns . Happy Birthday, MSG!! Happy Birthday, MSG!! and many happy returns . Now det(H) is equal to the volume of the n-dimensional parallelepiped spanned by the rows of H. By assumption, each row has Euclidean length at most n1/2, so that det(H) ≤ nn/2; equality holds if and only if I every entry of H is ±1; > I the rows of H are orthogonal, that is, HH = nI. A matrix attaining the bound is a Hadamard matrix. This is a nice example of a continuous problem whose solution brings us into discrete mathematics. Hadamard's theorem Let H be an n × n matrix, all of whose entries are at most 1 in modulus. How large can det(H) be? A matrix attaining the bound is a Hadamard matrix. This is a nice example of a continuous problem whose solution brings us into discrete mathematics. Hadamard's theorem Let H be an n × n matrix, all of whose entries are at most 1 in modulus. How large can det(H) be? Now det(H) is equal to the volume of the n-dimensional parallelepiped spanned by the rows of H. By assumption, each row has Euclidean length at most n1/2, so that det(H) ≤ nn/2; equality holds if and only if I every entry of H is ±1; > I the rows of H are orthogonal, that is, HH = nI.
    [Show full text]
  • On D. G. Higman's Note on Regular 3-Graphs
    Also available at http://amc.imfm.si ISSN 1855-3966 (printed edn.), ISSN 1855-3974 (electronic edn.) ARS MATHEMATICA CONTEMPORANEA 6 (2013) 99–115 On D. G. Higman’s note on regular 3-graphs Daniel Kalmanovich Department of Mathematics Ben-Gurion University of the Negev 84105 Beer Sheva, Israel Received 17 October 2011, accepted 25 April 2012, published online 4 June 2012 Abstract We introduce the notion of a t-graph and prove that regular 3-graphs are equivalent to cyclic antipodal 3-fold covers of a complete graph. This generalizes the equivalence of regular two-graphs and Taylor graphs. As a consequence, an equivalence between cyclic antipodal distance regular graphs of diameter 3 and certain rank 6 commutative association schemes is proved. New examples of regular 3-graphs are presented. Keywords: Antipodal graph, association scheme, distance regular graph of diameter 3, Godsil- Hensel matrix, group ring, Taylor graph, two-graph. Math. Subj. Class.: 05E30, 05B20, 05E18 1 Introduction This paper is mainly a clarification of [6] — a short draft written by Donald Higman in 1994, entitled “A note on regular 3-graphs”. The considered generalization of two-graphs was introduced by D. G. Higman in [5]. As in the famous correspondence between two-graphs and switching classes of simple graphs, t-graphs are interpreted as equivalence classes of an appropriate switching relation defined on weights, which play the role of simple graphs. In his note Higman uses certain association schemes to characterize regular 3-graphs and to obtain feasibility conditions for their parameters. Specifically, he provides a graph theoretic interpretation of a weight and from the resulted graph he constructs a rank 4 symmetric association scheme and a rank 6 fission of it.
    [Show full text]
  • 2020 Ural Workshop on Group Theory and Combinatorics
    Institute of Natural Sciences and Mathematics of the Ural Federal University named after the first President of Russia B.N.Yeltsin N.N. Krasovskii Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences The Ural Mathematical Center 2020 Ural Workshop on Group Theory and Combinatorics Yekaterinburg – Online, Russia, August 24-30, 2020 Abstracts Yekaterinburg 2020 2020 Ural Workshop on Group Theory and Combinatorics: Abstracts of 2020 Ural Workshop on Group Theory and Combinatorics. Yekaterinburg: N.N. Krasovskii Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences, 2020. DOI Editor in Chief Natalia Maslova Editors Vladislav Kabanov Anatoly Kondrat’ev Managing Editors Nikolai Minigulov Kristina Ilenko Booklet Cover Desiner Natalia Maslova c Institute of Natural Sciences and Mathematics of Ural Federal University named after the first President of Russia B.N.Yeltsin N.N. Krasovskii Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences The Ural Mathematical Center, 2020 2020 Ural Workshop on Group Theory and Combinatorics Conents Contents Conference program 5 Plenary Talks 8 Bailey R. A., Latin cubes . 9 Cameron P. J., From de Bruijn graphs to automorphisms of the shift . 10 Gorshkov I. B., On Thompson’s conjecture for finite simple groups . 11 Ito T., The Weisfeiler–Leman stabilization revisited from the viewpoint of Terwilliger algebras . 12 Ivanov A. A., Densely embedded subgraphs in locally projective graphs . 13 Kabanov V. V., On strongly Deza graphs . 14 Khachay M. Yu., Efficient approximation of vehicle routing problems in metrics of a fixed doubling dimension .
    [Show full text]
  • The Road to Deterministic Matrices with the Restricted Isometry Property
    Air Force Institute of Technology AFIT Scholar Faculty Publications 2013 The Road to Deterministic Matrices with the Restricted Isometry Property Afonso S. Bandeira Matthew C. Fickus Air Force Institute of Technology Dustin G. Mixon Percy Wong Follow this and additional works at: https://scholar.afit.edu/facpub Part of the Mathematics Commons Recommended Citation Bandeira, A. S., Fickus, M., Mixon, D. G., & Wong, P. (2013). The Road to Deterministic Matrices with the Restricted Isometry Property. Journal of Fourier Analysis and Applications, 19(6), 1123–1149. https://doi.org/10.1007/s00041-013-9293-2 This Article is brought to you for free and open access by AFIT Scholar. It has been accepted for inclusion in Faculty Publications by an authorized administrator of AFIT Scholar. For more information, please contact [email protected]. THE ROAD TO DETERMINISTIC MATRICES WITH THE RESTRICTED ISOMETRY PROPERTY AFONSO S. BANDEIRA, MATTHEW FICKUS, DUSTIN G. MIXON, AND PERCY WONG Abstract. The restricted isometry property (RIP) is a well-known matrix condition that provides state-of-the-art reconstruction guarantees for compressed sensing. While random matrices are known to satisfy this property with high probability, deterministic constructions have found less success. In this paper, we consider various techniques for demonstrating RIP deterministically, some popular and some novel, and we evaluate their performance. In evaluating some techniques, we apply random matrix theory and inadvertently find a simple alternative proof that certain random matrices are RIP. Later, we propose a particular class of matrices as candidates for being RIP, namely, equiangular tight frames (ETFs). Using the known correspondence between real ETFs and strongly regular graphs, we investigate certain combinatorial implications of a real ETF being RIP.
    [Show full text]
  • Spectra of Graphs
    Spectra of graphs Andries E. Brouwer Willem H. Haemers 2 Contents 1 Graph spectrum 11 1.1 Matricesassociatedtoagraph . 11 1.2 Thespectrumofagraph ...................... 12 1.2.1 Characteristicpolynomial . 13 1.3 Thespectrumofanundirectedgraph . 13 1.3.1 Regulargraphs ........................ 13 1.3.2 Complements ......................... 14 1.3.3 Walks ............................. 14 1.3.4 Diameter ........................... 14 1.3.5 Spanningtrees ........................ 15 1.3.6 Bipartitegraphs ....................... 16 1.3.7 Connectedness ........................ 16 1.4 Spectrumofsomegraphs . 17 1.4.1 Thecompletegraph . 17 1.4.2 Thecompletebipartitegraph . 17 1.4.3 Thecycle ........................... 18 1.4.4 Thepath ........................... 18 1.4.5 Linegraphs .......................... 18 1.4.6 Cartesianproducts . 19 1.4.7 Kronecker products and bipartite double. 19 1.4.8 Strongproducts ....................... 19 1.4.9 Cayleygraphs......................... 20 1.5 Decompositions............................ 20 1.5.1 Decomposing K10 intoPetersengraphs . 20 1.5.2 Decomposing Kn into complete bipartite graphs . 20 1.6 Automorphisms ........................... 21 1.7 Algebraicconnectivity . 22 1.8 Cospectralgraphs .......................... 22 1.8.1 The4-cube .......................... 23 1.8.2 Seidelswitching. 23 1.8.3 Godsil-McKayswitching. 24 1.8.4 Reconstruction ........................ 24 1.9 Verysmallgraphs .......................... 24 1.10 Exercises ............................... 25 3 4 CONTENTS 2 Linear algebra 29 2.1
    [Show full text]
  • Sixth(A) Edition
    A Mathematical Bibliography of Signed and Gain Graphs and Allied Areas Compiled by Thomas Zaslavsky Manuscript prepared with Marge Pratt Department of Mathematical Sciences Binghamton University Binghamton, New York, U.S.A. 13902-6000 E-mail: [email protected] Submitted: March 19, 1998; Accepted: July 20, 1998. Sixth Edition, Revision a 20 July 1998 Mathematical Subject Classifications (1991): Primary 05-02, 05C99; Secondary 05B20, 05B25, 05B35, 05C10, 05C15, 05C20, 05C25, 05C30, 05C35, 05C38, 05C45, 05C50, 05C60, 05C65, 05C70, 05C75, 05C80, 05C85, 05C90, 05E25, 05E30, 06A07, 06A09, 05C10, 15A06, 15A15, 15A39, 15A99, 20B25, 20F55, 34C11, 51D20, 51E20, 52B12, 52B30, 52B40, 52C07, 68Q15, 68Q25, 68Q35, 68R10, 82B20, 82D30, 90A08, 90B10, 90C08, 90C27, 90C35, 90C60, 92D40, 92E10, 92H30, 92J10, 92K10, 94B25. Colleagues: HELP! If you have any suggestions whatever for items to include in this bibliography, or for other changes, please let me hear from you. Thank you. Index A 1 H 48 O 83 V 110 B 8 I 59 P 84 W 111 C 20 J 60 Q 90 X 118 D 28 K 63 R 90 Y 118 E 32 L 71 S 94 Z 115 F 36 M 76 T 104 G 39 N 82 U 109 Preface A signed graph is a graph whose edges are labeled by signs. This is a bibliography of signed graphs and related mathematics. I regard as fundamental the notion of balance of a circuit (sign product equals +, the sign group identity) and the vertex-edge incidence matrix (whose column for a negative edge has two +1's or two −1's, for a positive edge one +1 and one −1, the rest being zero).
    [Show full text]
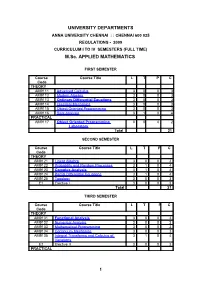
  • UNIVERSITY DEPARTMENTS M.Sc. APPLIED MATHEMATICS
    UNIVERSITY DEPARTMENTS ANNA UNIVERSITY CHENNAI : : CHENNAI 600 025 REGULATIONS - 2009 CURRICULUM I TO IV SEMESTERS (FULL TIME) M.Sc. APPLIED MATHEMATICS FIRST SEMESTER Course Course Title L T P C Code THEORY AM9111 Advanced Calculus 3 0 0 3 AM9112 Modern Algebra 3 0 0 3 AM9113 Ordinary Differential Equations 3 0 0 3 AM9114 Classical Mechanics 3 0 0 3 AM9115 Object Oriented Programming 3 0 0 3 AM9116 Real Analysis 3 1 0 4 PRACTICAL AM9117 Object Oriented Programming 0 0 4 2 Laboratory Total 21 SECOND SEMESTER Course Course Title L T P C Code THEORY AM9121 Linear Algebra 3 0 0 3 AM9122 Probability and Random Processes 3 1 0 4 AM9123 Complex Analysis 3 1 0 4 AM9124 Partial Differential Equations 3 1 0 4 AM9125 Topology 3 0 0 3 E1 Elective I 3 0 0 3 Total 21 THIRD SEMESTER Course Course Title L T P C Code THEORY AM9131 Functional Analysis 3 0 0 3 AM9132 Numerical Analysis 3 0 0 3 AM9133 Mathematical Programming 3 0 0 3 AM9134 Continuum Mechanics 3 0 0 3 AM9135 Integral Transforms and Calculus of 3 1 0 4 Variations E2 Elective II 3 0 0 3 PRACTICAL 1 AM9136 Computational Laboratory 0 0 4 2 AM9137 Seminar 0 0 2 1 Total 22 FOURTH SEMESTER Course Course Title L T P C Code THEORY E3 Elective III 3 0 0 3 E4 Elective IV 3 0 0 3 AM9141 Project 0 0 20 10 Total 16 Total Credits: 80 ELECTIVES Course Course Title L T P C Code AM9151 Metric Spaces and Fixed Point Theory 3 0 0 3 AM9152 Discrete Mathematics 3 0 0 3 AM9153 Number theory 3 0 0 3 AM9154 Mathematical Statistics 3 0 0 3 AM9155 Stochastic Processes 3 0 0 3 AM9156 Formal Languages and Automata
    [Show full text]
  • 69 Adjacency Matrix
    Index A-optimality, 439 angle between matrices, 168 absolute error, 484, 494, 526 angle between vectors, 37, 229, 357 ACM Transactions on Mathematical ANSI (standards), 475, 562, 563 Software, 552, 617 Applied Statistics algorithms, 617 adj(·), 69 approximation and estimation, 431 adjacency matrix, 331–334, 390 approximation of a matrix, 174, 257, Exercise 8.20:, 396 339, 437, 533 augmented, 390 approximation of a vector, 41–43 adjoint (see also conjugate transpose), arithmetic mean, 35, 37 59 Arnoldi method, 318 adjoint, classical (see also adjugate), 69 artificial ill-conditioning, 269 adjugate, 69, 598 ASCII code, 460 adjugate and inverse, 118 association matrix, 328–338, 357, 365, affine group, 115, 179 366, 369–371 affine space, 43 adjacency matrix, 331–332, 390 affine transformation, 228 connectivity matrix, 331–332, 390 Aitken’s integral, 217 dissimilarity matrix, 369 AL(·) (affine group), 115 distance matrix, 369 algebraic multiplicity, 144 incidence matrix, 331–332, 390 similarity matrix, 369 algorithm, 264, 499–513 ATLAS (Automatically Tuned Linear batch, 512 Algebra Software), 555 definition, 509 augmented adjacency matrix, 390 direct, 264 augmented connectivity matrix, 390 divide and conquer, 506 Automatically Tuned Linear Algebra greedy, 506 Software (ATLAS), 555 iterative, 264, 508–511, 564 autoregressive process, 447–450 reverse communication, 564 axpy, 12, 50, 83, 554, 555 online, 512 axpy elementary operator matrix, 83 out-of-core, 512 real-time, 512 back substitution, 274, 406 algorithmically singular, 121 backward error analysis,
    [Show full text]