Master's Thesis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bibliography from ADS File: Lambert.Bib August 16, 2021 1
Bibliography from ADS file: lambert.bib Reddy, A. B. S. & Lambert, D. L., “VizieR Online Data Cata- August 16, 2021 log: Abundance ratio for 5 local stellar associations (Reddy+, 2015)”, 2018yCat..74541976R ADS Reddy, A. B. S., Giridhar, S., & Lambert, D. L., “VizieR Online Data Deepak & Lambert, D. L., “Lithium in red giants: the roles of the He-core flash Catalog: Line list for red giants in open clusters (Reddy+, 2015)”, and the luminosity bump”, 2021arXiv210704624D ADS 2017yCat..74504301R ADS Deepak & Lambert, D. L., “Lithium in red giants: the roles of the He-core flash Ramírez, I., Yong, D., Gutiérrez, E., et al., “Iota Horologii Is Unlikely to Be an and the luminosity bump”, 2021MNRAS.tmp.1807D ADS Evaporated Hyades Star”, 2017ApJ...850...80R ADS Deepak & Lambert, D. L., “Lithium abundances and asteroseismology of red gi- Ramya, P., Reddy, B. E., Lambert, D. L., & Musthafa, M. M., “VizieR On- ants: understanding the evolution of lithium in giants based on asteroseismic line Data Catalog: Hercules stream K giants analysis (Ramya+, 2016)”, parameters”, 2021MNRAS.505..642D ADS 2017yCat..74601356R ADS Federman, S. R., Rice, J. S., Ritchey, A. M., et al., “The Transition Hema, B. P., Pandey, G., Kamath, D., et al., “Abundance Analyses of from Diffuse Molecular Gas to Molecular Cloud Material in Taurus”, the New R Coronae Borealis Stars: ASAS-RCB-8 and ASAS-RCB-10”, 2021ApJ...914...59F ADS 2017PASP..129j4202H ADS Bhowmick, A., Pandey, G., & Lambert, D. L., “Fluorine detection in hot extreme Pandey, G. & Lambert, D. L., “Non-local Thermodynamic Equilibrium Abun- helium stars”, 2020JApA...41...40B ADS dance Analyses of the Extreme Helium Stars V652 Her and HD 144941”, Reddy, A. -

Analysis of Stellar Activity and Orbital Dynamics in Extrasolar Planetary Systems
Analysis of Stellar Activity and Orbital Dynamics in Extrasolar Planetary Systems Dissertation zur Erlangung des Doktorgrades des Department Physik der Universität Hamburg vorgelegt von Sebastian Schröter aus Lübeck, Schleswig-Holstein Hamburg 2012 Gutachter der Dissertation: Prof. Dr. J. H. M. M. Schmitt Prof. Dr. A. Reiners Gutachter der Disputation: Prof. Dr. P. H. Hauschildt Prof. Dr. R. Banerjee Datum der Disputation: 04.05.2012 Vorsitzender des Prüfungsausschusses: Dr. R. Baade Vorsitzender des Promotionsausschusses: Prof. Dr. P. H. Hauschildt Dekan der MIN Fakultät: Prof. Dr. H. Graener Zusammenfassung Das Forschungsgebiet der extrasolaren Planeten, dessen Anfänge weniger als zwei Jahr- zehnte zurückliegen, erlebt zur Zeit eine rasante Entwicklung ausgelöst durch Weltraum- teleskope wie CoRoT und Kepler. Diese Observatorien überwachen Tausende von Ster- nen über lange Zeiträume mit bisher unerreichbarer Genauigkeit und Zeitauflösung, um Sternbedeckungen durch Planeten zu beobachten. Magnetische Aktivität des Sterns kann einen bedeutenden Einfluss auf die Entwicklung eines Sternsystems mit eng umlaufenden Planeten haben. Die hochenergetische Strah- lung führt zu Evaporationsprozessen und Massenverlust in der Atmosphäre des Planeten. Extrasolare Planetensysteme mit einem aktiven Stern sind dann besonders interessant, wenn der Planet die Sternscheibe bei einem Transit bedeckt. In diesem Fall ermöglicht der Planet, die räumliche Auflösung von durch Aktivität bedingten Strukturen in pho- tosphärischen, chromosphärischen und koronalen Schichten -
Fy05 Accomplishments and Fy06 Plans Helmut A. Abt
Appendix A NOAO SCIENTIFIC STAFF: FY05 ACCOMPLISHMENTS AND FY06 PLANS ¬New appointment in FY05 S Non-NSF (external) funding ±Term ended in FY05 HELMUT A. ABT, Emeritus Astronomer Research Interests Evolutionary stellar problems, stellar characteristics, publication studies FY05 Accomplishments Abt and C. Boonyarak (U. Thailand) studied rotation velocities of stars in binaries. It was known that those with periods shorter than several days all have synchronized rotational and orbital motions. They found that binaries with periods up to 500 days have reduced rotational velocities due to tidal interactions. Abt found that the eccentricities in binaries vary from zero in close binaries to an average of 0.5 in binaries with periods greater than 1000 days. In the initial formation of binaries, all eccentricities are equally probable. FY06 Plans Abt is trying to understand the hot inner disks that occur around, at any one time, one-quarter of the rapidly- rotating A dwarfs. These disks have no connection with the outer cool dust disks found around many stars like Vega and beta Pictoris. These disks come and go on time scales of decades. Such stars do not occur in the low-density Local Interstellar Bubble, so they are material accreted from the interstellar medium. Theoretical aspects of the physical processes is being done with M. Marlborough (U. Western Ontario). TAFT E. ARMANDROFF, Astronomer (Director, NOAO Gemini Science Center) Research Interests Stellar populations in the Galaxy and nearby galaxies; dwarf spheroidal galaxies; globular clusters FY05 Accomplishments Armandroff has been studying the dwarf spheroidal satellite galaxies of M31 in collaboration with Da Costa (RSAA/ANU), Pritzl (Macalester), and Jacoby (WIYN). -

219Th Meeting of the American Astronomical Society
219TH MEETING OF THE AMERICAN ASTRONOMICAL SOCIETY 8-12 JANUARY 2012 AUSTIN, TX All scientific sessions will be held at the: Austin Convention Center COUNCIL .......................... 2 500 East Cesar Chavez Street Austin, TX 78701-4121 EXHIBITORS ..................... 4 AAS Paper Sorters ATTENDEE SERVICES .......................... 9 Tom Armstrong, Blaise Canzian, Thayne Curry, Shantanu Desai, Aaron Evans, Nimish P. Hathi, SCHEDULE .....................15 Jason Jackiewicz, Sebastien Lepine, Kevin Marvel, Karen Masters, J. Allyn Smith, Joseph Tenn, SATURDAY .....................25 Stephen C. Unwin, Gerritt Vershuur, Joseph C. Weingartner, Lee Anne Willson SUNDAY..........................28 Session Numbering Key MONDAY ........................36 90s Sunday TUESDAY ........................91 100s Monday WEDNESDAY .............. 146 200s Tuesday 300s Wednesday THURSDAY .................. 199 400s Thursday AUTHOR INDEX ........ 251 Sessions are numbered in the Program Book by day and time. Please note, posters are only up for the day listed. Changes after 7 December 2011 are only included in the online program materials. 1 AAS Officers & Councilors President (6/2010-6/2013) Debra Elmegreen Vassar College Vice President (6/2009-6/2012) Lee Anne Willson Iowa State Univ. Vice President (6/2010-6/2013) Nicholas B. Suntzeff Texas A&M Univ. Vice President (6/2011-6/2014) Edward B. Churchwell Univ. of Wisconsin Secretary (6/2010-6/2013) G. Fritz Benedict Univ. of Texas, Austin Treasurer (6/2008-6/2014) Hervey (Peter) Stockman STScI Education Officer (6/2006-6/2012) Timothy F. Slater Univ. of Wyoming Publications Board Chair (6/2011-6/2015) Anne P. Cowley Arizona State Univ. Executive Officer (6/2006-Present) Kevin Marvel AAS Councilors Richard G. French Wellesley College (6/2009-6/2012) James D. -

Variable Star Section Circular
British Astronomical Association VARIABLE STAR SECTION CIRCULAR No 138, December 2008 Contents V1251 Cygni Outburst ............................................................. inside front cover From the Director ............................................................................................... 1 Colloquium on Studying Southern Variables ...................................................... 2 Eclipsing Binary News ...................................................................................... 2 Variable Star Workshop ..................................................................................... 4 Why Variable Stars ................................................................................ 4 Introduction to CCD Observing ........................................................................ 5 Variable Star Spectroscopy and the Epsilon Aurigae Eclipse ............................. 6 EW Eclipsing Binaries: Constructing a Light Curve ........................................... 9 Effects of Varying Observing Conditions on Observing Stellar Magnitudes.....10 The Historic Outbursts of T Coronae Borealis Revisited ................................ 13 W Cephei Light Curves .................................................................................... 18 Chart News........................................................................................................19 The Current Period of OO Aquilae .................................................................. 21 KP Cassiopeiae Outburst ................................................................................ -

The Evolution of Compact Binary Star Systems
The Evolution of Compact Binary Star Systems Konstantin A. Postnov Moscow M.V.Lomonosov State University Sternberg Astronomical Institute 13 Universitetskij Pr. 119992 Moscow Russia email: [email protected] http://www.sai.msu.ru Lev R. Yungelson Institute of Astronomy of Russian Academy of Sciences 48 Pyatnitskaya Str. 119017 Moscow Russia email: [email protected] http://www.inasan.ru Abstract We review the formation and evolution of compact binary stars consisting of white dwarfs (WDs), neutron stars (NSs), and black holes (BHs). Mergings of compact binary stars are expected to be the most important sources for the forthcoming gravitational-wave (GW) as- tronomy. In the first part of the review, we discuss observational manifestations of close binary stars with NS and/or black components and their merger rate, crucial points in the formation and evolution of compact stars in binary systems, including the treatment of the natal kicks which NSs and BHs acquire during the core collapse of massive stars and the common envelope phase of binary evolution, which are most relevant to the merging rates of NS-NS, NS-BH and BH-BH binaries. The second part of the review is devoted mainly to formation and evolution of binary WDs and their observational manifestations, including their role as progenitors of cosmologically important thermonuclear SN Ia. We also consider AM CVn-stars which are thought to be the best verification binary GW sources for future low-frequency GW space interferometers. Update (11 October 2013) arXiv:1403.4754v2 [astro-ph.HE] 21 Mar 2014 Major revision, updated and expanded. References are updated by 2007 { early-2014 publications, some outdated items removed. -

Variable Star Section Circular
British Astronomical Association VARIABLE STAR SECTION CIRCULAR No 139, March 2009 Contents R CrB light curve from VSS observations of 1906 ................... inside front cover From the Director ............................................................................................... 1 Recurrent Object Programme News ................................................................... 4 Eclipsing Binary News ...................................................................................... 8 RASNZ revives it’s Variable Star Section ....................................................... 10 Seven New Variable Stars in Cygnus .................................................. 12 WR140 at Periastron ....................................................................................... 25 CSS 081231:071126+440405 ........................................................................... 26 Chart News - R Coronae Borealis .................................................................... 28 R Coronae Borealis - One Hundred Years Ago ................................................. 29 Edinburgh Variable Star Workshop ................................................................... 31 Observing Variable Stars with Binoculars ........................................................ 31 Why Observe Visually in the 21st Century........................................................ 36 The Visual Experiment ..................................................................................... 38 IBVS 5821 - 5846 ............................................................................................ -

NASA Goddard Space Flight Center Laboratory for High Energy Astrophysics Greenbelt, Maryland 20771
1 NASA Goddard Space Flight Center Laboratory for High Energy Astrophysics Greenbelt, Maryland 20771 ͓S0002-7537͑93͒00551-7͔ This report covers the period from July 1, 2001 to June Jones, Joseph Dodoo, Stephen Drake, Michael Harris, Ilana 30, 2002. Harrus, Hans Krimm, John Krizmanic, James Lochner, Tho- This Laboratory’s scientific research is directed toward mas McGlynn, Alex Moiseev, Koji Mukai, Kirpal Nandra, experimental and theoretical investigations in the areas of Chris Shrader, Alan Smale, Steven Snowden, Yang Soong, X-ray, gamma-ray, gravitational wave and cosmic-ray astro- Martin Still, Steve Sturner, and Georg Weidenspointner. physics. The range of interests of the scientists includes the The following investigators are University of Maryland Sun and the solar system, stellar objects, binary systems, Scientists: Drs. Keith Arnaud, David Band ͑UMBC͒, Simon neutron stars, black holes, the interstellar medium, normal Bandler, Patricia Boyd ͑UMBC͒, John Cannizzo ͑UMBC͒, and active galaxies, galaxy clusters, cosmic ray particles, James Chiang ͑UMBC͒, David Davis ͑UMBC͒, Ian George gravitational wave astrophysics, extragalactic background ra- ͑UMBC͒, Una Hwang, Taro Kotani ͑UMBC͒, Kip Kuntz diation, and cosmology. Scientists and engineers in the Labo- ͑UMBC͒, Michael Loewenstein, Craig Markwardt, Igor ratory also serve the scientific community, including project Moskalenko ͑UMBC͒, Chee Ng, Patrick Palmeri, Christo- support such as acting as project scientists and providing pher Reynolds, Ian Richardson, Jane Turner ͑UMBC͒, and technical assistance for various space missions. Also at any Tahir Yaqoob ͑now JHU͒. one time, there are typically between ten and fifteen graduate Visiting scientists from other institutions: Drs. Hilary students involved in Ph.D. research work in this Laboratory. -

Downloaded on 2017-09-05T00:30:50Z Physics in the Extreme: X-Ray and Optical Studies of Magnetic White Dwarfs and Related Objects
Title Physics in the extreme: X-ray and optical studies of magnetic white dwarfs and related objects Author(s) Kennedy, Mark Publication date 2017 Original citation Kennedy, M. 2017. Physics in the extreme: X-ray and optical studies of magnetic white dwarfs and related objects. PhD Thesis, University College Cork. Type of publication Doctoral thesis Rights © 2017, Mark Kennedy. http://creativecommons.org/licenses/by-nc-nd/3.0/ Embargo information No embargo required Item downloaded http://hdl.handle.net/10468/4038 from Downloaded on 2017-09-05T00:30:50Z Physics in the extreme: X-ray and optical studies of magnetic white dwarfs and related objects Mark Kennedy BSC 109482792 ¡ NATIONAL UNIVERSITY OF IRELAND, CORK SCHOOL OF SCIENCE DEPARTMENT OF PHYSICS Thesis submitted in partial fulfilment of the requirement for the degree of Doctor of Philosophy March 2017 Head of Department: Prof. John McInerney Supervisors: Prof. Paul Callanan Prof. Peter Garnavich External Examiner: Dr. Chris Watson Queen’s University Belfast Internal Examiner: Dr. Asaf Pe’er University College Cork Research supported by The Naughton Foundation Contents Contents List of Figures...............................v List of Tables............................... viii Abstract..................................x Acknowledgements............................ xii 1 Introduction1 1.1 Observational Properties of Binary Systems...........3 1.1.1 Non-magnetic CVs.....................3 1.1.1.1 Dwarf Novae...................3 1.1.1.2 Nova-likes....................6 1.1.1.3 SW Sextantis Systems..............6 1.1.2 Magnetic CVs........................7 1.1.2.1 Polar (AM Her) Stars..............7 1.1.2.2 DQ Her Stars...................8 1.1.3 Low Mass X-ray Binaries..................8 1.2 Roche lobe geometry of accreting systems............9 1.2.1 X-ray Luminosity-Accretion Rate relation........ -
Planetary Data
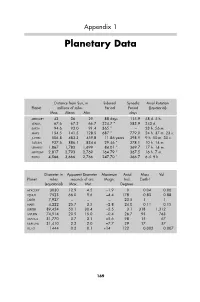
Appendix 1 Planetary Data Distance from Sun, in Sidereal Synodic Axial Rotation Planet millions of miles Period Period (Equatorial) Max. Mean Min. days MERCURY 43 36 29 88 days 115.9 58 d. 5 h. VENUS 67.6 67.2 66.7 224.7 ” 583.9 243 d. EARTH 94.6 93.0 91.4 365 ” – 23 h. 56 m. MARS 154.5 141.5 128.5 687 ” 779.9 24 h. 37 m. 23 s. JUPITER 506.8 483.3 459.8 11.86 years 398.9 9 h. 50 m. 30 s. SATURN 937.6 886.1 834.6 29.46 ” 378.1 10 h. 14 m. URANUS 1,867 1,783 1,699 84.01 ” 369.7 17 h. 14 m. NEPTUNE 2,817 2,793 2,769 164.79 ” 367.5 16 h. 7 m. PLUTO 4,566 3,666 2,766 247.70 ” 366.7 6 d. 9 h. Diameter in Apparent Diameter Maximum Axial Mass Vol. Planet miles seconds of arc Magn. Incl. Earth-I (equatorial) Max. Min. Degrees MERCURY 3030 12.9 4.5 –1.9 0 0.04 0.06 VENUS 7523 66.0 9.6 –4.4 178 0.83 0.88 EARTH 7,927 – – – 23.5 1 1 MARS 4,222 25.7 3.5 –2.8 24.0 0.11 0.15 JUPITER 89,424 50.1 30.4 –2.5 3.1 318 1,312 SATURN 74,914 20.9 15.0 –0.4 26.7 95 763 URANUS 31,770 3.7 3.1 +5.6 98 15 67 NEPTUNE 31,410 2.2 2.0 +7.7 29 17 57 PLUTO 1444 0.2 0.1 +14 122 0.002 0.007 169 Appendix 2 Planetary Satellites of Magnitude 14.5 or Brighter Name Mean distance Orbital Orbital Orbital Diameter, Magnitude from centre Period Eccentricity Inclination, (Longest) of primary el thousands of miles dh m degrees miles EARTH Moon 239.0 27 7 43 0.055 5.1 2160 –12.5 MARS Phobos 5.8 0 7 39 0.02 1.1 17 11.8 Deimos 14.6 1 6 18 0.003 1.8 9 12.8 JUPITER Io 262 1 18 28 0.004 0.04 2264 5.0 Europa 417 3 13 14 0.009 0.47 1945 5.3 Ganymede 666 7 3 43 0.002 0.21 3274 4.6 Callisto 1170 -

ASCA Observation of MS 1603.6+ 2600 (= UW Coronae Borealis): A
Accepted for Publication in ApJ. ASCA Observation of MS 1603.6+2600 (=UW Coronae Borealis): a Dipping Low-Mass X-ray Binary in the Outer Halo? Koji Mukai1, Alan P. Smale1, Caroline K. Stahle Code 662, NASA/Goddard Space Flight Center, Greenbelt, MD 20771. Eric M. Schlegel Harvard Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138. Rudy Wijnands2 Center for Space Research, Massachusetts Institute for Technology, 77 Massachusetts Avenue, Cambridge, MA 02139. ABSTRACT MS 1603.6+2600 is a high-latitude X-ray binary with a 111 min orbital period, thought to be either an unusual cataclysmic variable or an unusual low-mass X-ray binary. In an ASCA observation in 1997 August, we find a burst, whose light curve suggests a Type I (thermonuclear flash) origin. We also find an orbital X-ray modulation in MS 1603.6+2600, which is likely to be periodic dips, presumably due to azimuthal structure in the accretion disk. Both are consistent with this system being a normal low-mass X-ray binary harboring a neutron star, but at a great distance. We tentatively suggest that MS 1603.6+2600 is located in the outer halo of the Milky Way, perhaps associated with the globular cluster Palomar 14, 11◦ away from MS 1603.6+2600 on the arXiv:astro-ph/0107354v1 18 Jul 2001 sky at an estimated distance of 73.8 kpc. Subject headings: X-rays: stars — stars: individual (MS 1603.6+2600=UW CrB) 1. Introduction MS 1603.6+2600 was first discovered in the course of the Extended Medium Sensitivity Survey (Gioia et al 1990).