DOCSLIB.ORG

PHASE Diagram & PHASE RULE

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PHASE Diagram & PHASE RULE PHASE DIaGRAM & PHASE RULE MATERIAL SC (MM1101) ASSIGNMENT Submitted to - Dr. Ranjit Prasad Presented by :- Shashank Karan : 2020UGCS023 Akhilesh Kumar Mishra : 2020UGCS053 Harsh Bajaj : 2020UGCS083 Ravi Kumar : 2020UGCS113 INTRODUCTION Before, dip diving into the topic lets first know what is PHASE ? ¤ A phase can be defined as a homogeneous portion of a system that has uniform physical and chemical characteristics i.e. it is a physically distinct from other phases, chemically homogeneous and mechanically separable portion of a system. For example Let consider H₂O : it exsits as ice in solid , water as liquid and vapour as a gas . ¤ Different phases or of same phase of different component can be mixed to form another substance with unique property these are called solution or mixture . These can liquid-liquid, liquid-solid, liquid-gas, solid-solid , solid-liquid, solid-gas, gas- liquid , gas-gas and gas-solid composition. A solution (liquid or solid) is phase with more than one component; a mixture is a material with more than one phase Here in the given chapter we would be discussing about the phase change , their transformation , their kinetics the set of rules describing their changes and ultimately going through one Phase Diagram of Iron- carbon System. INTRODUCTION TO PHASE DIAGRAM A diagram that depicts existence of different phases of a system under equilibrium is termed as Phase Diagram. ¤ It is actually a collection of solubility limit curves. It is also known as equilibrium or constitutional diagram. ¤ Equilibrium phase diagrams represent the relationships between temperature, compositions and the quantities of phases at equilibrium. ¤ These diagrams do not indicate the dynamics when one phase transforms into another. ¤ Useful terminology related to phase diagrams: liquidus, solidus, solvus, terminal solid solution, invariant reaction, , inter-metallic compound, etc. ¤ Phase diagrams are classified according to the number of component present in a particular system. Here is the naming, we will be discussing it later. Single Component System – Unary Phase Diagram Two Component System – Binary Phase Diagram Three Component System – Tertiary Phase Diagram Four Component System – Quarter Phase Diagram IMPORTANT TERMINOLOGY AND SOME FEATURES OF A PHASE DIAGRAM 1. LIQUIDUS -– The liquidus is the temperature at which an alloy is completely melted. 2. SOLIDUS - The solidus is the highest temperature at which an alloy is solid. 3.Terminal Solid Solution - Solid phases (α and β) that exist near the ends of phase diagrams are called terminal solid solutions . 4.Invariant Reaction Reaction that occurs under equilibrium conditions at a specific temperature and specific composition which can not be varied. Important information, useful in materials development and selection, obtainable from a phase diagram: - It shows phases present at different compositions and temperatures under slow cooling (equilibrium) conditions. - It indicates equilibrium solid solubility of one element/compound in another. - It suggests temperature at which an alloy starts to solidify and the range of solidification. - It signals the temperature at which different phases start to melt. - Amount of each phase in a two-phase mixture can be obtained. Unary phase diagram If a system consists of just one component (e.g.: water), equilibrium of phases exist is depicted by unary phase diagram. The component may exist in different forms, thus variables here are – temperature and pressure. BINARY PHASE DIAGRAM If a system consists of two components, equilibrium of phases exist is depicted by binary phase diagram. For most systems, pressure is constant, thus independently variable parameters are – temperature and composition. Two components can be either two metals (Cu and Ni), or a metal and a compound (Fe and Fe3C), or two compounds (Al2O3 and Si2O3), etc. Two component systems are classified based on extent of mutual solid solubility – (a) completely soluble in both liquid and solid phases (isomorphous system) and (b) completely soluble in liquid phase whereas solubility is limited in solid state. For isomorphous system - E.g.: Cu-Ni, Ag-Au, Ge-Si , Al2O3,etc. GIBBS’S PHASE RULE In 1875, Josiah Williard Gibbs published a general principle governing systems in the thermodynamic equilibrium called the Phase Rule in a paper tilted on the Equilibrium of Heterogeneous Substances . “In a system under a set of conditions, number of phases (P) exist can be related to the number of components (C) and degrees of freedom (F)” by Gibbs phase rule. Where , Degrees of freedom refers to the number of independent variables (e.g.: pressure, temperature) that can be varied individually to effect changes in a system. Thermodynamically derived Gibbs phase rule: P+F = C+2 In practical conditions for metallurgical and materials systems, pressure can be treated as a constant (1 atm.). Thus Condensed Gibbs phase rule is written as: P+F = C+1 Hume-Ruthery conditions Hume-Rothery rules, named after William Hume-Rothery, are a set of basic rules that describe the conditions under which an element could dissolve in a metal, forming a solid solution. There are two sets of rules; one refers to substitutional solid solutions, and the other refers to interstitial solid solutions. For substitutional solid solutions, the Hume-Rothery rules are as follows: 1. The atomic radius of the solute and solvent atoms must differ by no more than 15% ( ) ( ) %difference = x 100% ( ) 2. The crystal structures of solute and solvent must be similar. 3. Complete solubility occurs when the solvent and solute have the same valency. A metal is more likely to dissolve a metal of higher valency, than vice versa. 4. The solute and solvent should have similar electronegativity. If the electronegativity difference is too great, the metals tend to form intermetallic compounds instead of solid solutions. For interstitial solid solutions, the Hume-Rothery Rules are: 1. Solute atoms should have a smaller radius than 59% of the radius of solvent atoms. 2. The solute and solvent should have similar electronegativity. 3. Valency factor: two elements should have the same valence. The greater the difference in valence between solute and solvent atoms, the lower the solubility. Fundamentally these are restricted to binary systems that form either substitutional or interstitial solid solutions. However, this approach limits assessing advanced alloys which are commonly multicomponent systems. Free energy diagrams (or phase diagrams) offer in-depth knowledge of equilibrium restraints in complex systems. LEVER’S RULE The lever rule is a rule used to determine the mole fraction (xi) or the mass fraction (wi) of each phase of a binary equilibrium phase diagram. It can be used to determine the fraction of liquid and solid phases for a given binary composition and temperature that is between the liquidus and solidus line In an alloy or a mixture with two phases, α and β, which themselves contain two elements, A and B, the lever rule states that the mass fraction of the α phase is a B a w = ( wb-wb ) /( wb ) where a ● wb is the mass fraction of element B in the a phase b ● wb is the mass fraction of element B in the β phase ● wb is the mass fraction of element B in the entire alloy or mixture all at some fixed temperature or pressure. Procedure to find equilibrium relative amounts of phases (lever rule): - A tie-line is constructed across the two phase region at the temperature of the alloy to intersect the region boundaries. The relative amount of a phase is computed by taking the length of tie line from overall composition to the phase boundary for the other phase, and dividing by the total tieline length. In previous figure, relative amount of liquid and solid phases is given respectively by: VARIENT REACTIONS Observed triple point in unary phase diagram for water? How about eutectic point in binary phase diagram? These points are specific in the sense that they occur only at that particular conditions of concentration, temperature, pressure etc. Try changing any of the variable, it does not exist i.e. phases are not equilibrium any more! Hence they are known as invariant points, and represents invariant reactions. Invariant reactions result in different product phases: terminal phases and intermediate phases. Intermediate phases are either of varying composition (intermediate solid solution) or fixed composition (intermetallic compound). Occurrence of intermediate phases cannot be readily predicted from the nature of the pure components! Inter-metallic compounds differ from other chemical compounds in that the bonding is primarily metallic rather than ionic or covalent. E.g.: Fe3C is metallic, whereas MgO is covalent. When using the lever rules, inter-metallic compounds are treated like any other phase. Fe-C binary system – Phase transformations Fe-Fe3C phase diagram is characterized by five individual phases,: α–ferrite (BCC) Fe-C solid solution, γ-austenite (FCC) Fe-C solid solution, δ-ferrite (BCC) Fe-C solid solution, Fe3C (iron carbide) or cementite - an inter-metallic compound and liquid Fe-C solution and four invariant reactions: - peritectic reaction at 1495 C and 0.16%C, δ-ferrite + L ↔ γ-iron (austenite) - monotectic reaction 1495 C and 0.51%C, L ↔ L + γ-iron (austenite) - eutectic reaction at 1147 C and 4.3 %C, L ↔ γ-iron + Fe3C (cementite) [ledeburite] - eutectoid reaction at 723 C and 0.8%C, γ-iron ↔ α– ferrite + Fe3C (cementite) [pearlite] Fe-C alloys CLASSIFICATION Fe-C alloys are classified according to wt.% C present in the alloy for technological convenience as follows: Commercial pure irons % C < 0.008 Low-carbon/mild steels 0.008 - %C - 0.3 Medium carbon steels 0.3 - %C - 0.8 High-carbon steels 0.8- %C - 2.11 Cast irons 2.11 < %C Cast irons that were slowly cooled to room temperature consists of cementite, look whitish – white cast iron. If it contains graphite, look grayish – gray cast iron. It is heat treated to have graphite in form of nodules – malleable cast iron.
Load more

Recommended publications
  • Thermodynamics
    TREATISE ON THERMODYNAMICS BY DR. MAX PLANCK PROFESSOR OF THEORETICAL PHYSICS IN THE UNIVERSITY OF BERLIN TRANSLATED WITH THE AUTHOR'S SANCTION BY ALEXANDER OGG, M.A., B.Sc., PH.D., F.INST.P. PROFESSOR OF PHYSICS, UNIVERSITY OF CAPETOWN, SOUTH AFRICA THIRD EDITION TRANSLATED FROM THE SEVENTH GERMAN EDITION DOVER PUBLICATIONS, INC. FROM THE PREFACE TO THE FIRST EDITION. THE oft-repeated requests either to publish my collected papers on Thermodynamics, or to work them up into a comprehensive treatise, first suggested the writing of this book. Although the first plan would have been the simpler, especially as I found no occasion to make any important changes in the line of thought of my original papers, yet I decided to rewrite the whole subject-matter, with the inten- tion of giving at greater length, and with more detail, certain general considerations and demonstrations too concisely expressed in these papers. My chief reason, however, was that an opportunity was thus offered of presenting the entire field of Thermodynamics from a uniform point of view. This, to be sure, deprives the work of the character of an original contribution to science, and stamps it rather as an introductory text-book on Thermodynamics for students who have taken elementary courses in Physics and Chemistry, and are familiar with the elements of the Differential and Integral Calculus. The numerical values in the examples, which have been worked as applications of the theory, have, almost all of them, been taken from the original papers; only a few, that have been determined by frequent measurement, have been " taken from the tables in Kohlrausch's Leitfaden der prak- tischen Physik." It should be emphasized, however, that the numbers used, notwithstanding the care taken, have not vii x PREFACE.
    [Show full text]
  • Lecture 15: 11.02.05 Phase Changes and Phase Diagrams of Single- Component Materials
    3.012 Fundamentals of Materials Science Fall 2005 Lecture 15: 11.02.05 Phase changes and phase diagrams of single- component materials Figure removed for copyright reasons. Source: Abstract of Wang, Xiaofei, Sandro Scandolo, and Roberto Car. "Carbon Phase Diagram from Ab Initio Molecular Dynamics." Physical Review Letters 95 (2005): 185701. Today: LAST TIME .........................................................................................................................................................................................2� BEHAVIOR OF THE CHEMICAL POTENTIAL/MOLAR FREE ENERGY IN SINGLE-COMPONENT MATERIALS........................................4� The free energy at phase transitions...........................................................................................................................................4� PHASES AND PHASE DIAGRAMS SINGLE-COMPONENT MATERIALS .................................................................................................6� Phases of single-component materials .......................................................................................................................................6� Phase diagrams of single-component materials ........................................................................................................................6� The Gibbs Phase Rule..................................................................................................................................................................7� Constraints on the shape of
    [Show full text]
  • Phase Diagrams
    Module-07 Phase Diagrams Contents 1) Equilibrium phase diagrams, Particle strengthening by precipitation and precipitation reactions 2) Kinetics of nucleation and growth 3) The iron-carbon system, phase transformations 4) Transformation rate effects and TTT diagrams, Microstructure and property changes in iron- carbon system Mixtures – Solutions – Phases Almost all materials have more than one phase in them. Thus engineering materials attain their special properties. Macroscopic basic unit of a material is called component. It refers to a independent chemical species. The components of a system may be elements, ions or compounds. A phase can be defined as a homogeneous portion of a system that has uniform physical and chemical characteristics i.e. it is a physically distinct from other phases, chemically homogeneous and mechanically separable portion of a system. A component can exist in many phases. E.g.: Water exists as ice, liquid water, and water vapor. Carbon exists as graphite and diamond. Mixtures – Solutions – Phases (contd…) When two phases are present in a system, it is not necessary that there be a difference in both physical and chemical properties; a disparity in one or the other set of properties is sufficient. A solution (liquid or solid) is phase with more than one component; a mixture is a material with more than one phase. Solute (minor component of two in a solution) does not change the structural pattern of the solvent, and the composition of any solution can be varied. In mixtures, there are different phases, each with its own atomic arrangement. It is possible to have a mixture of two different solutions! Gibbs phase rule In a system under a set of conditions, number of phases (P) exist can be related to the number of components (C) and degrees of freedom (F) by Gibbs phase rule.
    [Show full text]
  • Phase Transitions in Multicomponent Systems
    Physics 127b: Statistical Mechanics Phase Transitions in Multicomponent Systems The Gibbs Phase Rule Consider a system with n components (different types of molecules) with r phases in equilibrium. The state of each phase is defined by P,T and then (n − 1) concentration variables in each phase. The phase equilibrium at given P,T is defined by the equality of n chemical potentials between the r phases. Thus there are n(r − 1) constraints on (n − 1)r + 2 variables. This gives the Gibbs phase rule for the number of degrees of freedom f f = 2 + n − r A Simple Model of a Binary Mixture Consider a condensed phase (liquid or solid). As an estimate of the coordination number (number of nearest neighbors) think of a cubic arrangement in d dimensions giving a coordination number 2d. Suppose there are a total of N molecules, with fraction xB of type B and xA = 1 − xB of type A. In the mixture we assume a completely random arrangement of A and B. We just consider “bond” contributions to the internal energy U, given by εAA for A − A nearest neighbors, εBB for B − B nearest neighbors, and εAB for A − B nearest neighbors. We neglect other contributions to the internal energy (or suppose them unchanged between phases, etc.). Simple counting gives the internal energy of the mixture 2 2 U = Nd(xAεAA + 2xAxBεAB + xBεBB) = Nd{εAA(1 − xB) + εBBxB + [εAB − (εAA + εBB)/2]2xB(1 − xB)} The first two terms in the second expression are just the internal energy of the unmixed A and B, and so the second term, depending on εmix = εAB − (εAA + εBB)/2 can be though of as the energy of mixing.
    [Show full text]
  • Introduction to Phase Diagrams*
    ASM Handbook, Volume 3, Alloy Phase Diagrams Copyright # 2016 ASM InternationalW H. Okamoto, M.E. Schlesinger and E.M. Mueller, editors All rights reserved asminternational.org Introduction to Phase Diagrams* IN MATERIALS SCIENCE, a phase is a a system with varying composition of two com- Nevertheless, phase diagrams are instrumental physically homogeneous state of matter with a ponents. While other extensive and intensive in predicting phase transformations and their given chemical composition and arrangement properties influence the phase structure, materi- resulting microstructures. True equilibrium is, of atoms. The simplest examples are the three als scientists typically hold these properties con- of course, rarely attained by metals and alloys states of matter (solid, liquid, or gas) of a pure stant for practical ease of use and interpretation. in the course of ordinary manufacture and appli- element. The solid, liquid, and gas states of a Phase diagrams are usually constructed with a cation. Rates of heating and cooling are usually pure element obviously have the same chemical constant pressure of one atmosphere. too fast, times of heat treatment too short, and composition, but each phase is obviously distinct Phase diagrams are useful graphical representa- phase changes too sluggish for the ultimate equi- physically due to differences in the bonding and tions that show the phases in equilibrium present librium state to be reached. However, any change arrangement of atoms. in the system at various specified compositions, that does occur must constitute an adjustment Some pure elements (such as iron and tita- temperatures, and pressures. It should be recog- toward equilibrium. Hence, the direction of nium) are also allotropic, which means that the nized that phase diagrams represent equilibrium change can be ascertained from the phase dia- crystal structure of the solid phase changes with conditions for an alloy, which means that very gram, and a wealth of experience is available to temperature and pressure.
    [Show full text]
  • Phase Diagrams of Ternary -Conjugated Polymer Solutions For
    polymers Article Phase Diagrams of Ternary π-Conjugated Polymer Solutions for Organic Photovoltaics Jung Yong Kim School of Chemical Engineering and Materials Science and Engineering, Jimma Institute of Technology, Jimma University, Post Office Box 378 Jimma, Ethiopia; [email protected] Abstract: Phase diagrams of ternary conjugated polymer solutions were constructed based on Flory-Huggins lattice theory with a constant interaction parameter. For this purpose, the poly(3- hexylthiophene-2,5-diyl) (P3HT) solution as a model system was investigated as a function of temperature, molecular weight (or chain length), solvent species, processing additives, and electron- accepting small molecules. Then, other high-performance conjugated polymers such as PTB7 and PffBT4T-2OD were also studied in the same vein of demixing processes. Herein, the liquid-liquid phase transition is processed through the nucleation and growth of the metastable phase or the spontaneous spinodal decomposition of the unstable phase. Resultantly, the versatile binodal, spinodal, tie line, and critical point were calculated depending on the Flory-Huggins interaction parameter as well as the relative molar volume of each component. These findings may pave the way to rationally understand the phase behavior of solvent-polymer-fullerene (or nonfullerene) systems at the interface of organic photovoltaics and molecular thermodynamics. Keywords: conjugated polymer; phase diagram; ternary; polymer solutions; polymer blends; Flory- Huggins theory; polymer solar cells; organic photovoltaics; organic electronics Citation: Kim, J.Y. Phase Diagrams of Ternary π-Conjugated Polymer 1. Introduction Solutions for Organic Photovoltaics. Polymers 2021, 13, 983. https:// Since Flory-Huggins lattice theory was conceived in 1942, it has been widely used be- doi.org/10.3390/polym13060983 cause of its capability of capturing the phase behavior of polymer solutions and blends [1–3].
    [Show full text]
  • Section 1 Introduction to Alloy Phase Diagrams
    Copyright © 1992 ASM International® ASM Handbook, Volume 3: Alloy Phase Diagrams All rights reserved. Hugh Baker, editor, p 1.1-1.29 www.asminternational.org Section 1 Introduction to Alloy Phase Diagrams Hugh Baker, Editor ALLOY PHASE DIAGRAMS are useful to exhaust system). Phase diagrams also are con- terms "phase" and "phase field" is seldom made, metallurgists, materials engineers, and materials sulted when attacking service problems such as and all materials having the same phase name are scientists in four major areas: (1) development of pitting and intergranular corrosion, hydrogen referred to as the same phase. new alloys for specific applications, (2) fabrica- damage, and hot corrosion. Equilibrium. There are three types of equili- tion of these alloys into useful configurations, (3) In a majority of the more widely used commer- bria: stable, metastable, and unstable. These three design and control of heat treatment procedures cial alloys, the allowable composition range en- conditions are illustrated in a mechanical sense in for specific alloys that will produce the required compasses only a small portion of the relevant Fig. l. Stable equilibrium exists when the object mechanical, physical, and chemical properties, phase diagram. The nonequilibrium conditions is in its lowest energy condition; metastable equi- and (4) solving problems that arise with specific that are usually encountered inpractice, however, librium exists when additional energy must be alloys in their performance in commercial appli- necessitate the knowledge of a much greater por- introduced before the object can reach true stabil- cations, thus improving product predictability. In tion of the diagram. Therefore, a thorough under- ity; unstable equilibrium exists when no addi- all these areas, the use of phase diagrams allows standing of alloy phase diagrams in general and tional energy is needed before reaching meta- research, development, and production to be done their practical use will prove to be of great help stability or stability.
    [Show full text]
  • Phase Diagrams a Phase Diagram Is Used to Show the Relationship Between Temperature, Pressure and State of Matter
    Phase Diagrams A phase diagram is used to show the relationship between temperature, pressure and state of matter. Before moving ahead, let us review some vocabulary and particle diagrams. States of Matter Solid: rigid, has definite volume and definite shape Liquid: flows, has definite volume, but takes the shape of the container Gas: flows, no definite volume or shape, shape and volume are determined by container Plasma: atoms are separated into nuclei (neutrons and protons) and electrons, no definite volume or shape Changes of States of Matter Freezing start as a liquid, end as a solid, slowing particle motion, forming more intermolecular bonds Melting start as a solid, end as a liquid, increasing particle motion, break some intermolecular bonds Condensation start as a gas, end as a liquid, decreasing particle motion, form intermolecular bonds Evaporation/Boiling/Vaporization start as a liquid, end as a gas, increasing particle motion, break intermolecular bonds Sublimation Starts as a solid, ends as a gas, increases particle speed, breaks intermolecular bonds Deposition Starts as a gas, ends as a solid, decreases particle speed, forms intermolecular bonds http://phet.colorado.edu/en/simulation/states- of-matter The flat sections on the graph are the points where a phase change is occurring. Both states of matter are present at the same time. In the flat sections, heat is being removed by the formation of intermolecular bonds. The flat points are phase changes. The heat added to the system are being used to break intermolecular bonds. PHASE DIAGRAMS Phase diagrams are used to show when a specific substance will change its state of matter (alignment of particles and distance between particles).
    [Show full text]
  • Acid Dissociation Constant - Wikipedia, the Free Encyclopedia Page 1
    Acid dissociation constant - Wikipedia, the free encyclopedia Page 1 Help us provide free content to the world by donating today ! Acid dissociation constant From Wikipedia, the free encyclopedia An acid dissociation constant (aka acidity constant, acid-ionization constant) is an equilibrium constant for the dissociation of an acid. It is denoted by Ka. For an equilibrium between a generic acid, HA, and − its conjugate base, A , The weak acid acetic acid donates a proton to water in an equilibrium reaction to give the acetate ion and − + HA A + H the hydronium ion. Key: Hydrogen is white, oxygen is red, carbon is gray. Lines are chemical bonds. K is defined, subject to certain conditions, as a where [HA], [A−] and [H+] are equilibrium concentrations of the reactants. The term acid dissociation constant is also used for pKa, which is equal to −log 10 Ka. The term pKb is used in relation to bases, though pKb has faded from modern use due to the easy relationship available between the strength of an acid and the strength of its conjugate base. Though discussions of this topic typically assume water as the solvent, particularly at introductory levels, the Brønsted–Lowry acid-base theory is versatile enough that acidic behavior can now be characterized even in non-aqueous solutions. The value of pK indicates the strength of an acid: the larger the value the weaker the acid. In aqueous a solution, simple acids are partially dissociated to an appreciable extent in in the pH range pK ± 2. The a actual extent of the dissociation can be calculated if the acid concentration and pH are known.
    [Show full text]
  • Lecture 36. the Phase Rule
    Lecture 36. The Phase Rule P = number of phases C = number of components (chemically independent constituents) F = number of degrees of freedom xC,P = the mole fraction of component C in phase P The variables used to describe a system in equilibrium: x11, x21, x31,...,xC −1,1 phase 1 x12 , x22 , x32 ,..., xC−1,2 phase 2 x1P , x2P , x3P ,...,xC−1,P phase P T,P Total number of variables = P(C-1) + 2 Constraints on the system: m11 = m12 = m13 =…= m1,P P - 1 relations m21 = m22 = m23 =…= m2,P P - 1 relations mC,1 = mC,2 = mC,3 =…= mC,P P - 1 relations 1 Total number of constraints = C(P - 1) Degrees of freedom = variables - constraints F=P(C- 1) + 2 - C(P - 1) F=C- P+2 Single Component Systems: F = 3 - P In single phase regions, F = 2. Both T and P may vary. At the equilibrium between two phases, F = 1. Changing T requires a change in P, and vice versa. At the triple point, F = 0. Tt and Pt are unique. 2 Four phases cannot be in equilibrium (for a single component.) Two Component Systems: F = 4 - P The possible phases are the vapor, two immiscible (or partially miscible) liquid phases, and two solid phases. (Of course, they don’t have to all exist. The liquids might turn out to be miscible for all compositions.) 3 Liquid-Vapor Equilibrium Possible degrees of freedom: T, P, mole fraction of A xA = mole fraction of A in the liquid yA = mole fraction of A in the vapor zA = overall mole fraction of A (for the entire system) We can plot either T vs zA holding P constant, or P vs zA holding T constant.
    [Show full text]
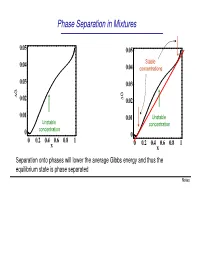
  • Phase Separation in Mixtures
    Phase Separation in Mixtures 0.05 0.05 0.04 Stable 0.04 concentrations 0.03 0.03 G G ∆ 0.02 ∆ 0.02 0.01 0.01 Unstable Unstable concentration concentration 0 0 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 x x Separation onto phases will lower the average Gibbs energy and thus the equilibrium state is phase separated Notes Phase Separation versus Temperature Note that at higher temperatures the region of concentrations where phase separation takes place shrinks and G eventually disappears T increases ∆G = ∆U −T∆S This is because the term -T∆S becomes large at high temperatures. You can say that entropy “wins” over the potential energy cost at high temperatures Microscopically, the kinetic energy becomes x much larger than potential at high T, and the 1 x2 molecules randomly “run around” without noticing potential energy and thus intermix Oil and water mix at high temperature Notes Liquid-Gas Phase Separation in a Mixture A binary mixture can exist in liquid or gas phases. The liquid and gas phases have different Gibbs potentials as a function of mole fraction of one of the components of the mixture At high temperatures the Ggas <Gliquid because the entropy of gas is greater than that of liquid Tb2 T At lower temperatures, the two Gibbs b1 potentials intersect and separation onto gas and liquid takes place. Notes Boiling of a binary mixture Bubble point curve Dew point If we have a liquid at pint A that contains F A gas curve a molar fraction x1 of component 1 and T start heating it: E D - First the liquid heats to a temperature T’ C at constant x A and arrives to point B.
    [Show full text]
  • Modeling of Phase Equilibria in Reactive Mixtures
    Sumitomo Chemical Co., Ltd. Modeling of Phase Equilibria in Industrial Technology & Research Laboratory Reactive Mixtures Tetsuya SUZUTA Most chemical processes contain at least two of the three phases of solid, liquid and gas. Therefore it is essen- tial to fully understand phase equilibria for the logical design of processes and apparatus. The basic theory of phase equilibrium has already been established, but there are some exceptions which are not compliant with the theory. Many of those are influenced by chemical reactions within a certain phase or between different phases, so consideration of the reaction is necessary for precise reproduction of such unusual behavior. In this paper, some models for phase equilibria in reactive mixtures and several examples of their application in industrial plants are presented. This paper is translated from R&D Report, “SUMITOMO KAGAKU”, vol. 2018. Introduction1), 2) Modeling of Phase Equilibria Involving Chemical Reaction There are three states of matter: solid; liquid; and gas. Phase equilibrium is defined as a state in which 1. Chemical Reaction in Phase Equilibria matter and heat are balanced between at least two During a chemical reaction, a substance recombines phases and each phase is present stably. The phase- the atoms and atomic groups by itself or mutually with equilibrium relationship of the temperature, pressure other substances and generates a new substance. Some and the component composition is one of the impor- chemical reactions involve the cleavage or formation of tant properties in chemical processes. Numerous covalent bonding, and some occur due to the changes measured data of phase equilibrium had been accumu- in ion bonding or hydrogen bonding.
    [Show full text]