DOCSLIB.ORG

B]<OU 160228 >M

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
B]<OU 160228 >M z </)> ro^ 160228 >m >*B]<OU ^S z ^g OSMANIA UNIVERSITY LIBRARY >5T /6 Call No. ^ _ . Accession No. Author Title This book should be returnedion or before the^date last marked below. H. B. E*HMOB KPATKHfi KYPC AHAJIHTHMECKOfi FEOMETPHM FOCy/lAPCTBEHHOE 4>H3HKO-MATEMATH4ECKOft ^HTEPATVPbl M o c K B a N. YEFIMOV A Brief Course in Analytic Geometry TRANSLATED FROM THE RUSSIAN by O. S R O K A PEACE PUBLISHERS MOSCOW Written by Professor N. Yefimov, Dr. Phys. Math. Sc., this book presents, in concise form, the theoretical foundations of plane and solid analytic geometry. Also, an elementary outline of the theory of determinants is given in the Appendix. The textbook is intended for students of higher educational institutions and for engineers engaged in the field of quadric surface design. The book is illustrated with 122 drawings. CONTENTS Part One PLANE ANALYTIC GEOMETRY Chapter 1. Coordinates on a Straight Line and in a Plane 11 1. An Axis and Segments of an Axis 11 2. Coordinates on a Line. The Number Axis 14 3. Rectangular Cartesian Coordinates in a Plane. A Note on Ob- lique Cartesian Coordinates 16 4. Polar Coordinates 20 Chapter 2. Elementary Problems of Plane Analytic Geometry 23 5. Projection of a Line Segment. Distance Between Two Points . 23 6. Calculation of the Area of a Triangle 28 7. Division of a Line Segment in a Given Ratio 30 8. Transformation of Cartesian Coordinates by Translation of Axes 35 9. Transformation of Rectangular Cartesian Coordinates by Rotation of Axes 36 10. Transformation of Rectangular Cartesian Coordinates by Change of Origin and Rotation of Axes 38 Chapter 3. The Equation of a Curve . 41 11. The Concept of the Equation of a Curve. Examples of Curves Represented by Equations 41 12. Examples of Deriving the Equation of a Given Curve 48 13. The Problem of the Intersection of Two Curves 50 14. Parametric Equations of a Curve 51 15. Algebraic Curves - . 52 Chapter 4. Curves of the First Order 55 16. The Slope of a Straight Line 55 17. The Slope-intercept Equation of a Straight Line 56 18. Calculation of the Angle Between Two Straight Lines. Conditions for the Parallelism and Perpendicularity of Two Straight Lines . 59 19. The Straight Line As the Curve of the First Order. The General Equation of the Straight Line 61 20. Incomplete Equations of the First Degree. The Intercept Equation of a Straight Line 63 21. Discussion of a System of Equations Representing Two Straight Lines .65 22. The Normal Equation of a Straight Line. The Problem of Cal- culating the Distance of a Point from a Straight Line 68 23. The Equation of a Pencil of Lines 71 Chapter 5. Geometric Properties of Curves of the Second Order 75 24. The Ellipse. Definition of the Ellipse and Derivation of Its Canon- ical Equation 75 6 Contents 25. Discussion of the Shape of the Ellipse 79 26. The Eccentricity of the Ellipse 81 27. Rational Expressions for Focal Radii of the Ellipse 82 28. Point-by-point Construction of the Ellipse. The Parametric Equations of the Ellipse 83 29. The Ellipse as the Projection of a Circle on a Plane. The Ellipse as the Section of a Circular Cylinder by a Plane 84 30. The Hyperbola. Definition of the Hyperbola and Derivation of Its Canonical Equation 87 31. Discussion of the Shape of the Hyperbola .91 32. The Eccentricity of the Hyperbola 97 33. Rational Expressions for Focal Radii of the Hyperbola 98 34. The Directrices of the Ellipse and Hyperbola 99 35. The Parabola. Derivation of the Canonical Equation of the Pa- rabola .103 36. Discussion of the Shape of the Parabola 105 37. The Polar Equation of the Ellipse, Hyperbola and Parabola . 107 38. Diameters of Curves of the Second Order 109 39. The Optical Properties of the Ellipse, Hyperbola and Parabola 114 40. The Ellipse, Hyperbola and Parabola as Conic Sections .... 115 Chapter 6. Transformation of Equations by Change of Coordinates .... 116 41. Examples of Reducing the General Equation of a Second-Order Curve to Canonical Form 116 42. The Hyperbola as the Inverse Proportionality Graph. The Pa- rabola as the Graph of a Quadratic Function 125 Part Two SOLID ANALYTIC GEOMETRY 7. Chapter Some Elementary Problems of Solid Analytic Geometry . 131 43. Rectangular Cartesian Coordinates in Space 131 44. The Concept of a Free Vector. The Projection of a Vector on an Axis 134 45. The Projections of a Vector on the Coordinate Axes 138 46. Direction Cosines .141 47. Distance between Two Points. Division of a Line Segment in a Given Ratio 142 Chapter 8. Linear Operations on Vectors 143 48. Definitions of Linear Operations 143 49. Basic Properties of Linear Operations 144 50. The Vector Difference 147 51. Fundamental Theorems on Projections . 149 52. Resolution of Vectors into Components 152 Chapter 9. The Scalar Product of Vectors 157 53. The Scalar Product and Its Basic Properties 157 54. Representation of the Scalar Product in Terms of the Coordi- nates of the Vector Factors 160 Chapter 10. The Vector and Triple Scalar Products of Vectors 163 55. The Vector Product and Its Basic Properties 163 56. Representation of the Vector Product in Terms of the Coordinates of the Vector Factors 170 Contents 57. The Triple Scalar Product .172 58. Representation of the Triple Scalar Product in Terms of the Coordinates of the Vector Factors 176 Chapter 1L The Equation of a Surface and the Equations of a Curve . 178 59. The Equation of a Surface 178 60. The Equations of a Curve. The Problem of the Intersection of Three Surfaces 179 61. The Equation of a Cylindrical Surface with Elements Parallel to a Coordinate Axis 181 62. Algebraic Surfaces 183 Chapter 12. The Plane as the Surface of the First Order. The Equations of a Straight Line 185 63. The Plane as the Surface of the First Order 185 64. Incomplete Equations of Planes. The Intercept Form of the Equa- tion of a Plane 188 65. The Normal Equation of a Plane. The Distance of a Point from a Plane 190 66, The Equations of a Straight Line 194 67. The Direction Vector of a Straight Line. The Canonical Equations of a Straight Line. The Parametric Equations of a Straight Line . 198 68. Some Additional Propositions and Examples 201 Chapter 13 Quadric Surfaces 207 69 The Ellipsoid and the Hyperboloids 207 70. The Quadric Cone 213 71. The Paraboloids 215 72. The Quadric Cylinders 219 73. The Rectilinear Generators of the Hyperboloid of One Sheet. The Shukhov Towers 220 Appendix. The Elements of the Theory of Determinants 225 1. Determinants of the Second Order and Systems of Two Equations of the First Degree in Two Unknowns 225 2. A Homogeneous System of Two Equations of the First Degree in Three Unknowns 229 3. Determinants of the Third Order 232 4. Cofactors and Minors 236 5. Solution and Analysis of a System of Three First-degree Equa- tions in Three Unknowns 240 6. The Concept of a Determinant of Any Order 217 PART ONE Plane Analytic Geometry Chapter 1 COORDINATES ON A STRAIGHT LINE AND IN A PLANE 1. An Axis and Segments of an Axis 1. Consider an arbitrary straight line. It extends in two oppo- site directions. Let us choose at will one of these directions and refer to it as positive (and to the other direction as negative). A straight line to which a positive direction has been assigned is called an axis. In diagrams, the positive direction of an axis is indicated by an arrowhead (see, for example, Fig. 1, where an axis a is shown). B Fig. 1. * 2. Let there be given an axis, and let there also be specified a unit segment, that is, a unit of length by means of which any segment can be measured, so that the length of any segment may be determined. Take two arbitrary points on a given axis and denote them by the letters A and B. The segment bounded by the points A, B is called a directed segment if one of these points has been designated as the initial point, and the other as the terminal point of the segment. A segment is considered to be directed from its initial to its terminal point. In the succeeding pages, a directed segment is denoted by the two letters that mark the points bounding the segment; the letter marking the initial point is always written first, and a horizontal bar is placed over the letters. Thus, AB denotes the directed seg- ment bounded by the points A, B and having A as its initial point; BA denotes the directed segment bounded by the points A, B and having B as its initial point. When dealing with directed segments of an axis in our future work, we shall often refer to them simply as segments, omitting the word "directed". Coordinates on a Straight Line and in a Plane Let us now agree to define the value of a segment AB of an axis as the number equal to the length of the segment and taken with a plus or minus sign according as the direction of the seg- ment agrees with the positive or the negative_direction of the axis. We shall denote the value of a segment AB by the symbol AB (without the horizontal bar). We do not exclude the case when the points A and B coincide; in this case, the segment AB is called a zero segment, since its value is equal to zero. A zero segment has no definite direction, and hence the term "directed" may be applied to such a segment only conventionally.
Load more

Recommended publications
  • Transformation of Axes
    19 Chapter 2 Transformation of Axes 2.1 Transformation of Coordinates It sometimes happens that the choice of axes at the beginning of the solution of a problem does not lead to the simplest form of the equation. By a proper transformation of axes an equation may be simplified. This may be accom- plished in two steps, one called translation of axes, the other rotation of axes. 2.1.1 Translation of axes Let ox and oy be the original axes and let o0x0 and o0y0 be the new axes, parallel respectively to the old ones. Also, let o0(h, k) referred to the origin of new axes. Let P be any point in the plane, and let its coordinates referred to the old axes be (x, y) and referred to the new axes be (x0y0) . To determine x and y in terms of x0, y0, h and x = h + x0 y = k + y0 20 Chapter 2. Transformation of Axes these equations represent the equations of translation and hence, the coeffi- cients of the first degree terms are vanish. 2.1.2 Rotation of axes Let ox and oy be the original axes and ox0 and oy0 the new axes. 0 is the origin for each set of axes. Let the angle x0 ox through which the axes have been rotated be represented by q. Let P be any point in the plane, and let its coordinates referred to the old axes be (x, y) and referred to the new axes be (x0, y0), To determine x and y in terms of x0, y0 and q : x = OM = ON − MN = x0 cos q − y0 sin q and y = MP = MM0 + M0P = NN0 + M0P = x0 sin q + y0 cos q 2.1.
    [Show full text]
  • General Theory of Conicoids 1
    GENERAL THEORY OF CONICOIDS Structure 1.1 Introduction Objectives 1.2 What is a Conicoid? 1.3 Change of Axes 1.3.1 Translat~on of Axes 1.3.2 Projection L 1.3.3 Rotation of Axes 1.4 Reduction to Standard Form 1.5 Summary 1.6 Solutions and Answers I 1.1 INTRODUCTION You have seen in Block 7 that the general equation of second degree in two variables x and y represents a conic. In analogy with this we can ask: what will a general second degree equation in three variables represent? In Block 8 you have studied some particular forms of second degree equations in three variables, namely, those representing spheres, cones and cylinders. In this unit we study the most general form of a second degree equation in three variables. The surface generated by these equations are called quadrics or conicoids. This name is apt because, as you will see in Unit 8, they can be formed by revolving a conic about a line called an axis. Alexis Clairaut (17 13- 1765), a French mathematician, was one of the pioneers to study quadric surfaces. He specified that a surface, in .general, can be represented by an equation in three variables. He presented his ideas in his book 'Recherche Sur Les Courbes a Double Courbure' in which he gave the equations of several conicoids like the sphere, cylinder, hyperboloid and ellipsoid. We start this unit with a small section in which we define a conicoid: In the next section we discuss rigid body motions in a three-dimensional system.
    [Show full text]
  • Vector Analysis: MS4613
    Vector Analysis: MS4613 Prof. S.B.G. O’Brien Main Building, B3041. References Advanced engineering mathematics, Kreyszig. Mathematics applied to continuum mechanics, Segel. Mathematical methods for physicists, Arfken. Mathematics applied to the deterministic sciences, Lin and Segel. Vectors and cartesian tensors, Bourne and Kendall. Vector Analysis (Schaum series), Murray and Spiegel. GREEK ALPHABET For each Greek letter, we illustrate the form of the capital letter and the form of the lower case letter. In some cases, there is a popular variation of the lower case letter. Greek Greek English Greek Greek English letter name equivalent letter name equivalent A α Alpha a N ν Nu n B β Beta b Ξ ξ Xi x Γ γ Gamma g O o Omicron o ∆ δ Delta d Π π ̟ Pi p E ǫ ε Epsilon e P ρ ̺ Rho r Z ζ Zeta z Σ σ ς Sigma s H η Eta e T τ Tau t Θ θ ϑ Theta th Υ υ Upsilon u I ι Iota i Φ φ ϕ Phi ph K κ Kappa k X χ Chi ch Λ λ Lambda l Ψ φ Psi ps M µ Mu m Ω ω Omega o Exam Papers: http://www.ul.ie/portal/students Some papers are also available at: http://www.staff.ul.ie/obriens/index.html 1 1 Rectangular cartesian coordinates and rotation of axes 1.1 Rectangular cartesian coordinates We wish to be able to describe locations and directions in space. From a fixed point O, called the origin (of coordinates), draw three fixed lines Ox,Oy,Oz at right angles to each other as in fig.1.1 and forming a right handed system (rectangular cartesian axes) (use RH screw rule as in fig.1.2).
    [Show full text]
  • C:\Book\Booktex\C1s3.DVI
    65 §1.3 SPECIAL TENSORS Knowing how tensors are defined and recognizing a tensor when it pops up in front of you are two different things. Some quantities, which are tensors, frequently arise in applied problems and you should learn to recognize these special tensors when they occur. In this section some important tensor quantities are defined. We also consider how these special tensors can in turn be used to define other tensors. Metric Tensor Define yi,i=1,...,N as independent coordinates in an N dimensional orthogonal Cartesian coordinate system. The distance squared between two points yi and yi + dyi,i=1,...,N is defined by the expression ds2 = dymdym =(dy1)2 +(dy2)2 + ···+(dyN )2. (1.3.1) Assume that the coordinates yi are related to a set of independent generalized coordinates xi,i=1,...,N by a set of transformation equations yi = yi(x1,x2,...,xN ),i=1,...,N. (1.3.2) To emphasize that each yi depends upon the x coordinates we sometimes use the notation yi = yi(x), for i =1,...,N. The differential of each coordinate can be written as ∂ym dym = dxj ,m=1,...,N, (1.3.3) ∂xj and consequently in the x-generalized coordinates the distance squared, found from the equation (1.3.1), becomes a quadratic form. Substituting equation (1.3.3) into equation (1.3.1) we find ∂ym ∂ym ds2 = dxidxj = g dxidxj (1.3.4) ∂xi ∂xj ij where ∂ym ∂ym g = ,i,j=1,...,N (1.3.5) ij ∂xi ∂xj i are called the metrices of the space defined by the coordinates x ,i=1,...,N.
    [Show full text]
  • Kaifangfa and Translation of Coordinate Axes 開方法과 座標軸의 平行移動
    Journal for History of Mathematics http://dx.doi.org/10.14477/jhm.2014.27.6.387 Vol. 27 No. 6 (Dec. 2014), 387–394 Kaifangfa and Translation of Coordinate Axes 開方法과 座標軸의 平行移動 Hong Sung Sa 홍성사 Hong Young Hee 홍영희 Chang Hyewon* 장혜원 Since ancient civilization, solving equations has become one of the most impor- tant subjects in mathematics and mathematics education. The extractions of square roots and cube roots were first dealt in Jiuzhang Suanshu in the setting ofsub- divisions. Extending these, Shisuo Kaifangfa and Zengcheng Kaifangfa were in- troduced in the 11th century and the subsequent development became one of the most important contributions to mathematics in the East Asian mathematics. The translation of coordinate axes plays an important role in school mathematics. Con- necting the translation and Kaifangfa, we find strong didactical implications for improving students’ understanding the history of Kaifangfa together with the trans- lation itself although the latter is irrelevant to the former’s historical development. Keywords: Shisuo Kaifangfa, Zengcheng Kaifangfa, Translation of coordinate axes, Fanji, Yiji; 釋鎖開方法, 增乘開方法, 座標軸의 平行移動, 飜積, 益積. MSC: 01A25, 12-03, 12E12, 97A30, 97G70, 97H30, 97N50 1 Introduction It is well known that the theory of equations is one of the most important subjects in the history of mathematics. It divides into two parts, namely, constructing equa- tions and solving them [3]. In this paper, our main concern is how to solve poly- nomial equations so that we will not discuss the former part. As also well known, the first attempt to solve equations was how to extract square roots and cube roots.
    [Show full text]
  • SECTION 9-4 Translation of Axes
    9-4 Translation of Axes 639 For the receiving antenna shown in the figure, the common focus F is located 120 feet above the vertex of the parabola, .and focus F؅ (for the hyperbola) is 20 feet above the vertex The vertex of the reflecting hyperbola is 110 feet above the vertex for the parabola. Introduce a coordinate system by using the axis of the parabola as the y axis (up positive), and let the x axis pass through the center of the hyperbola (right Radiotelescope positive). What is the equation of the reflecting hyperbola? Write y in terms of x. (b) SECTION 9-4 Translation of Axes • Translation of Axes • Standard Equations of Translated Conics • Graphing Equations of the Form Ax2 ϩ Cy2 ϩ Dx ϩ Ey ϩ F ϭ 0 • Finding Equations of Conics In the last three sections we found standard equations for parabolas, ellipses, and hyperbolas located with their axes on the coordinate axes and centered relative to the origin. What happens if we move conics away from the origin while keeping their axes parallel to the coordinate axes? We will show that we can obtain new standard equations that are special cases of the equation Ax2 ϩ Cy2 ϩ Dx ϩ Ey ϩ F ϭ 0, where A and C are not both zero. The basic mathematical tool used in this endeavor is translation of axes. The usefulness of translation of axes is not limited to graphing conics, however. Translation of axes can be put to good use in many other graphing situations. • Translation of Axes A translation of coordinate axes occurs when the new coordinate axes have the same direction as and are parallel to the original coordinate axes.
    [Show full text]
  • Mathematics Session
    Mathematics Session Cartesian Coordinate Geometry And Straight Lines Session Objectives 1. Cartesian Coordinate system and Quadrants 2. Distance formula 3. Area of a triangle 4. Collinearity of three points 5. Section formula 6. Special points in a triangle 7. Locus and equation to a locus 8. Translation of axes - shift of origin 9. Translation of axes - rotation of axes René Descartes Coordinates Y 3 Y-axis : Y’OY 2 X-axis : X’OX 1 +ve direction+ve X’ O X -4 -3 -2 -1 1 2 3 4 Origin -1 +ve direction -2 -ve direction ve directionve Y’ -3 - Coordinates Y 3 2 (2,1) Abcissa 1 X’ O X -4 -3 -2 -1 1 2 3 4 -1 Ordinate -2 (-3,-2) Y’ -3 (?,?) Coordinates Y 3 2 (2,1) Abcissa 1 X’ O X -4 -3 -2 -1 1 2 3 4 -1 Ordinate -2 (-3,-2) Y’ -3 (4,?) Coordinates Y 3 2 (2,1) Abcissa 1 X’ O X -4 -3 -2 -1 1 2 3 4 -1 Ordinate -2 (-3,-2) Y’ -3 (4,-2.5) Quadrants Y (-,+) (+,+) II I X’ O X III IV (-,-) (+,-) Y’ Quadrants Y (-,+) (+,+) II I X’ O X III IV (-,-) (+,-) Y’ Ist? IInd? Q : (1,0) lies in which Quadrant? A : None. Points which lie on the axes do not lie in any quadrant. Distance Formula Y 1 y - 2 y 2 y N PQN is a right angled . 1 x1 y 2 2 2 (x2-x1) PQ = PN + QN 2 2 2 X’ O X PQ = (x2-x1) +(y2-y1) x2 Y’ 22 PQ =( x2 − x 1) +( y 2 − y 1 ) Distance From Origin Distance of P(x, y) from the origin is 22 =(x − 0) +( y − 0) =+xy22 Applications of Distance Formula Parallelogram Applications of Distance Formula Rhombus Applications of Distance Formula Rectangle Applications of Distance Formula Square Area of a Triangle Y A(x1, y1) ) 2 , y , C(x3, y3) 2 B(x X’ O M L N
    [Show full text]
  • Unit 9 Will Be Followed by the Analytic Geometry Final Exam
    Topics In this unit, we continue our study of the conic sections with investigations on translation and rotation of axes. The course concludes with a study of parametric equations. x Translation of axes (10.2-4) o standard equation of a translated conic o finding axes, foci, etc., of translated conics o finding equations of translated conics x Rotation of axes (10.5, plus supplementary pamphlet) o general equation of a conic section o finding the angle of rotation o converting the equation of a rotated conic to the standard equation of a translated conic o finding axes, foci, etc., of rotated conics o identifying conics x Parametric equations (10.7) o definition of parametric equations o graphing a plane curve given by parametric equations o eliminating the parameter o projectile motion o finding parametric equations of conic sections Unit 9 will be followed by the Analytic Geometry Final Exam. Study Guidelines for the 8th edition of Sullivan's Precalculus These reading and problem assignments are designed to help you learn the course material. You should complete all of these problems, check your answers in the back of the textbook, and get help with the problems that you missed. Most of the problems are odd-numbered, so you can check the solutions in the Solutions Manual. The only way to learn mathematics is to do mathematics, so while these problems will not be collected or graded, you will probably not do well in the course if you do not complete these and check your work as described above. After completing these problems, go on to the Unit Exam Description below and follow directions.
    [Show full text]
  • Chapter 7: Identifying Second Degree Equations
    Chapter 7 Identifying second degree equations 7.1 The eigenvalue method In this section we apply eigenvalue methods to determine the geometrical nature of the second degree equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, (7.1) where not all of a, h, b are zero. a h Let A = be the matrix of the quadratic form ax2 + 2hxy + by2. h b · ¸ We saw in section 6.1, equation 6.2 that A has real eigenvalues λ1 and λ2, given by a + b (a b)2 + 4h2 a + b + (a b)2 + 4h2 λ1 = − − , λ2 = − . p 2 p 2 We show that it is always possible to rotate the x, y axes to x1, y1 axes whose positive directions are determined by eigenvectors X1 and X2 corresponding to λ1and λ2 in such a way that relative to the x1, y1 axes, equation 7.1 takes the form 2 2 a′x + b′y + 2g′x + 2f ′y + c = 0. (7.2) Then by completing the square and suitably translating the x1, y1 axes, to new x2, y2 axes, equation 7.2 can be reduced to one of several standard forms, each of which is easy to sketch. We need some preliminary definitions. 129 130 CHAPTER 7. IDENTIFYING SECOND DEGREE EQUATIONS DEFINITION 7.1.1 (Orthogonal matrix) An n n real matrix P is × called orthogonal if t P P = In. It follows that if P is orthogonal, then det P = 1. For ± det (P tP ) = det P t det P = ( det P )2, so (det P )2 = det I = 1.
    [Show full text]
  • Section 8.2. Applications to Geometry
    8.2 Applications to Geometry 1 Chapter 8. Eigenvalues: Further Applications and Computations 8.2. Applications to Geometry Note. Figure 8.2 shows there intersections of planes with a double right-circular cone (“right-circular” because a plane perpendicular to the axis of the cone cuts the cone in a circle). The resulting “conic sections” shown are an ellipse (a circle is a special case of an ellipse), a hyperbola, and a parabola. In this section we state the standard equations for these three conic sections without any derivation. For an alternated approach where definitions are given in terms of sums and differences of certain distances (and the derivation of our formulae follow from these definitions) see my online Calculus 3 notes: http://faculty.etsu.edu/gardnerr/2110/notes -12e/c11s6.pdf. 8.2 Applications to Geometry 2 Note. The equation of an ellipse in standard form (that is, with center at (0, 0)) is x2 y2 + = 1. a2 b2 If the center of the ellipse is at the point (h, k) then the equation is (x h)2 (y k)2 − + − = 1. a2 b2 See Figure 8.3. 2 2 Note. Every polynomial equation of the form c1x + c2y + c3x + c4y = d, where nonzero c1 an c2 are of the same sign, determines an ellipse. The center can be found by completing the square of the x2 and x terms and of the y2 and y terms. (x h)2 (y k)2 It’s possible for the equation to become of the form − + − = 0 in a2 b2 which case the solution set is the single point (h, k); this is called a degenerate (x h)2 (y k)2 ellipse.
    [Show full text]
  • Mehedi Sir Note on Coordinate Geometry.Pdf
    Faculty of Science and Information Technology Department of Natural Sciences Coordinate geometry is the branch of mathematics in which geometry is studied with the help of algebra. The great France mathematician and philosopher Rene Descartes (1596-1650) first applied algebraic formulae in geometry. A system of geometry where the position of points on the plane is described using two numbers called an ordered pair of numbers or coordinates. The first element of the ordered pair represents the distance of that point on x-axis called abscissa and second element on y-axis called ordinate. This abscissa and ordinate makes coordinates of that point. The method of describing the location of points in this way was proposed by the French mathematician René Descartes (1596 - 1650). (Pronounced "day CART"). He proposed further that curves and lines could be described by equations using this technique, thus being the first to link algebra and geometry. In honor of his work, the coordinates of a point are often referred to as its Cartesian coordinates and the coordinate plane as the Cartesian Coordinate Plane and coordinate geometry sometimes called Cartesian geometry. 1 Cartesian/Rectangular Coordinates System: Every plane is two dimensional so to locate the position of a point in a plane there is needed two coordinates. The Mathematician Rene Descartes first considered two perpendicular intersecting fixed straight lines in a plane as axes of coordinates. These two straight lines are named as rectangular axes and intersecting point as the origin denotes by the symbol O and the symbol O comes from the first letter of the word origin.
    [Show full text]
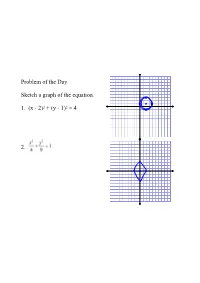
  • Problem of the Day Sketch a Graph of The
    Problem of the Day Sketch a graph of the equation. 1. (x ­ 2)2 + (y ­ 1)2 = 4 2. Problem of the Day Sketch a graph of the equation. 1. 16(x ­ 1)2 ­ 9(y + 2)2 = 144 Problem of the Day Write the equation. Ellipse with center (4,5), major axis length 10 and a focus at (6,5) Hyperbola with center (­1, 2), conjugate axis length 16, and a transverse axis length 8 and along the line y = 2 Problem of the Day Write the equation of the conic section in standard form x2 + y2 ­ 10x + 4y ­ 7 = 0 4x2 + y2 ­ 8x + 4y ­ 4 = 0 Standard Equations of Translated Conic Sections Hyperbolas Hyperbolas Transverse Axis Conjugate Axis Foci Graph the following conic section. Graph the following conic section. Find the coordinates of the foci. Find the length of the transverse and conjugate axes. Graph the following conic section. Find the coordinates of the foci. Find the length of the transverse and conjugate axes. Use completing the square to write the equation of the hyperbola in standard form. y2 ­ 4x2 + 8x ­ 2y = 67 5x2 ­ y2 + 30x ­ 4y = 84 Use completing the square to write the equation of the hyperbola in standard form. Then find the coordinates of the foci. x2 ­ 9y2 + 16x ­ 72y ­ 161 = 0 Use completing the square to write the equation of the hyperbola in standard form. Then find the coordinates of the foci. 8y2 ­ 7x2 ­ 32y + 42x ­ 87 = 0 Write the equation of the hyperbola using the following information. Center (5,6), Vertex at (9,6) and conjugate axis length 10 Vertices (­4,­1) and (­4,­5) and Foci (­4,0) and (­4,­6) Standard Equations of Translated Conic Sections Parabolas (y ­ k)2 = 4a(x ­ h) (x ­ h)2 = 4a(y ­ k) Circle (x ­ h)2 + (y ­ k)2 = r2 Ellipses Translation of Axes Identify the conic section as a parabola, circle, ellipse, or hyperbola based on the equation.
    [Show full text]