DOCSLIB.ORG

Approximation of Derivatives

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Approximation of Derivatives Approximation of Derivatives Spring 2012 © Ammar Abu-Hudrouss -Islamic ١ University Gaza Introduction IIR filter design techniques depend mainly on converting analogue filter to a digital one. Analogue filter can be described by three methods 1) Its system function. M k sk k 0 H a (s) N k sk k 0 2) By its impulse response which is related to the system function by st H a (s) ha (t)e dt ٢ Digital Signal Processing ٢ Slide ١ Introduction 3) By linear constant-coefficient differential equation d k y(t) M d k x(t) k k k k dt k 0 dt Each of these three characterizations leads to alternative method for converting the analog filter to its digital equivalents ٣ Digital Signal Processing ٣ Slide Introduction The system function Ha(s) is stable if all its poles lie in the left half of the s-plane. Hence, the conversion is effective if 1. The j axis in the s-plane map into the unit circle in the z-plane. 2. The left-half plane LHP of the s-plane map into the inside of a unit circle in the z-plane (i.e stable analogue filter will be converted to stable digital filter. ٤ Digital Signal Processing ٤ Slide ٢ Approximation of derivatives The simplest methods to convert an analogue filter to a digital filter is to convert the differential equation into equivalent difference equation. For the first derivative dy(t) y(nT) y(nT T) y(n) y(n 1) dt tnT T T y(t) H (s) s dy(t) dt 1 z 1 y(n) H (z) y(n) y(n 1) T T ٥ Digital Signal Processing ٥ Slide Approximation of derivatives For the analog derivative, the system function is given by H (s) s Whereas, the digital system function is H (z) (1 z 1 ) /T Which leads to 1 z 1 s T ٦ Digital Signal Processing ٦ Slide ٣ Approximation of derivatives The 2nd derivative is replaced by the second difference d 2 y(t) d dy(t) [y(nT ) y(nt T)]/ T [y(nT T ) y(nT 2T)]/T 2 dt dt dt t nT T y(n) 2y(n 1) y(n 2) T 2 In frequency domain this is equivalent to 2 1 2z 1 z 2 1 z 1 s 2 2 T T Then the kth derivative is equivalent frequency-domain relationship 1 k k 1 z s T ٧ Digital Signal Processing ٧ Slide Approximation of derivatives The system function for IIR filter obtained as a result of approximation of the derivatives is H (z) H (s) a s(1z 1 ) /T Let us investigate the implication of the mapping from the s-plane to the z-plane 1 z 1 sT Then the j axis is mapped into 1 z 1 jT 1 T j 1 2T 2 1 2T 2 ٨ Digital Signal Processing ٨ Slide ٤ Approximation of derivatives The y -axis in the s -plane is mapped into a circle of radius ½ and with centre z = ½. Any point in the left hand plane will be mapped to points inside that circle. So the resultant filter is stable ٩ Digital Signal Processing ٩ Slide Approximation of derivatives The possible locations of poles of the digital filter are confined to small frequencies. As consequence, the mapping is restricted to low-pass and band-pass filters with relatively small resonant frequencies. It is not possible to transform a high-pass analog filter into a corresponding high-pass digital filter. In attempt to overcome this limitations, more complex substitutions for the derivatives have been proposed such as dy(t) 1 L y(nT kT) y(nT kT) tnT k dt T k 1 T ١٠ Digital Signal Processing ١٠ Slide ٥ Approximation of derivatives The resulting mapping between the s-plane and the z-plane is now L 1 k k s k z z T k0 When z = ej j2 L s k sink j T k1 Which is pure imaginary, which means by carefully selecting ks, The j axis can be transformed into the unity circle. This can be done by using optimization ١١ Digital Signal Processing ١١ Slide Approximation of derivatives Example: Convert the analogue bandpass filter with system function 1 H s a (s 0.1)2 9 Into a digital IIR filter by substituting for the derivatives method 1 H (z) ((1 z 1 ) / T 0.1) 2 9 T 2 /(1 0.2T 9.01T 2 ) H (z) 2(1 0.1T ) 1 1 z 1 z 2 1 0.2T 9.01T 2 1 0.2T 9.01T 2 T should be less than or equal 0.1 for poles near the unity circle ١٢ Digital Signal Processing ١٢ Slide ٦ Approximation of derivatives Example: Convert the analogue bandpass filter in the previous example by use of the mapping 1 s z z 1 T Solution: by substituting for s in H(s), we obtain 1 H (z) ((z z 1 ) /T 0.1) 2 9 z 2T 2 H (z) z 4 0.2Tz 3 (2 9.01T 2 )z 2 0.2Tz 1 H (z) has four poles while H (s) has two poles which means that the conversion has led to more complex system ١٣ Digital Signal Processing ١٣ Slide ٧.
Load more

Recommended publications
  • Active Control of Loudspeakers: an Investigation of Practical Applications
    Downloaded from orbit.dtu.dk on: Dec 18, 2017 Active control of loudspeakers: An investigation of practical applications Bright, Andrew Paddock; Jacobsen, Finn; Polack, Jean-Dominique; Rasmussen, Karsten Bo Publication date: 2002 Document Version Early version, also known as pre-print Link back to DTU Orbit Citation (APA): Bright, A. P., Jacobsen, F., Polack, J-D., & Rasmussen, K. B. (2002). Active control of loudspeakers: An investigation of practical applications. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Active Control of Loudspeakers: An Investigation of Practical Applications Andrew Bright Ørsted·DTU – Acoustic Technology Technical University of Denmark Published by: Ørsted·DTU, Acoustic Technology, Technical University of Denmark, Building 352, DK-2800 Kgs. Lyngby, Denmark, 2002 3 This work is dedicated to the memory of Betty Taliaferro Lawton Paddock Hunt (1916-1999) and to Samuel Raymond Bright, Jr. (1936-2001) 4 5 Table of Contents Preface 9 Summary 11 Resumé 13 Conventions, notation, and abbreviations 15 Conventions......................................................................................................................................
    [Show full text]
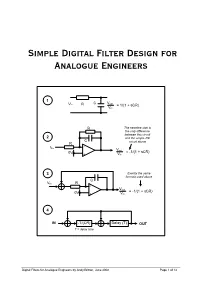
  • Simple Simple Digital Filter Design for Analogue Engineers
    Simple Digital Filter Design for Analogue Engineers 1 C Vout Vin R = 1/(1 + sCR) Vin R The negative sign is the only difference between this circuit 2 and the simple RC C R circuit above - Vin Vout 0V = -1/(1 + sCR) + Vin 3 Exactly the same formula used above C Vin R - Vout 0V = -1/(1 + sCR) + Vin 4 IN -T/(CR) Delay (T) OUT T = delay time Digital Filters for Analogue Engineers by Andy Britton, June 2008 Page 1 of 14 Introduction If I’d read this document years ago it would have saved me countless hours of agony and confusion understanding what should be conceptually very simple. My biggest discontent with topical literature is that they never cleanly relate digital filters to “real world” analogue filters. This article/document sets out to: - • Describe the function of a very basic RC low pass analogue filter • Convert this filter to an analogue circuit that is digitally realizable • Explain how analogue functions are converted to digital functions • Develop a basic 1st order digital low-pass filter • Develop a 2nd order filter with independent Q and frequency control parameters • Show how digital filters can be proven/designed using a spreadsheet such as excel • Demonstrate digital filters by showing excel graphs of signals • Explain the limitations of use of digital filters i.e. when they become unstable • Show how these filters fit in to the general theory (yawn!) Before the end of this article you should hopefully find something useful to guide you on future designs and allow you to successfully implement a digital filter.
    [Show full text]
  • Simulating the Directivity Behavior of Loudspeakers with Crossover Filters
    Audio Engineering Society Convention Paper Presented at the 123rd Convention 2007 October 5–8 New York, NY, USA The papers at this Convention have been selected on the basis of a submitted abstract and extended precis that have been peer reviewed by at least two qualified anonymous reviewers. This convention paper has been reproduced from the author's advance manuscript, without editing, corrections, or consideration by the Review Board. The AES takes no responsibility for the contents. Additional papers may be obtained by sending request and remittance to Audio Engineering Society, 60 East 42nd Street, New York, New York 10165-2520, USA; also see www.aes.org. All rights reserved. Reproduction of this paper, or any portion thereof, is not permitted without direct permission from the Journal of the Audio Engineering Society. Simulating the Directivity Behavior of Loudspeakers with Crossover Filters Stefan Feistel1, Wolfgang Ahnert2, and Charles Hughes3, and Bruce Olson4 1 Ahnert Feistel Media Group, Arkonastr.45-49, 13189 Berlin, Germany [email protected] 2 Ahnert Feistel Media Group, Arkonastr.45-49, 13189 Berlin, Germany [email protected] 3 Excelsior Audio Design & Services, LLC, Gastonia, NC, USA [email protected] 4 Olson Sound Design, Brooklyn Park, MN, USA [email protected] ABSTRACT In previous publications the description of loudspeakers was introduced based on high-resolution data, comprising most importantly of complex directivity data for individual drivers as well as of crossover filters. In this work it is presented how this concept can be exploited to predict the directivity balloon of multi-way loudspeakers depending on the chosen crossover filters.
    [Show full text]
  • Framsida Msc Thesis Viktor Gunnarsson
    Assessment of Nonlinearities in Loudspeakers Volume dependent equalization Master’s Thesis in the Master’s programme in Sound and Vibration VIKTOR GUNNARSSON Department of Civil and Environmental Engineering Division of Applied Acoustics Chalmers Room Acoustics Group CHALMERS UNIVERSITY OF TECHNOLOGY Göteborg, Sweden 2010 Master’s Thesis 2010:27 MASTER’S THESIS 2010:27 Assessment of Nonlinearities in Loudspeakers Volume dependent equalization VIKTOR GUNNARSSON Department of Civil and Environmental Engineering Division of Applied Acoustics Roomacoustics Group CHALMERS UNIVERSITY OF TECHNOLOGY Goteborg,¨ Sweden 2010 CHALMERS, Master’s Thesis 2010:27 ii Assessment of Nonlinearities in Loudspeakers Volume dependent equalization © VIKTOR GUNNARSSON, 2010 Master’s Thesis 2010:27 Department of Civil and Environmental Engineering Division of Applied Acoustics Roomacoustics Group Chalmers University of Technology SE-41296 Goteborg¨ Sweden Tel. +46-(0)31 772 1000 Reproservice / Department of Civil and Environmental Engineering Goteborg,¨ Sweden 2010 Assessment of Nonlinearities in Loudspeakers Volume dependent equalization Master’s Thesis in the Master’s programme in Sound and Vibration VIKTOR GUNNARSSON Department of Civil and Environmental Engineering Division of Applied Acoustics Roomacoustics Group Chalmers University of Technology Abstract Digital room correction of loudspeakers has become popular over the latest years, yield- ing great gains in sound quality in applications ranging from home cinemas and cars to audiophile HiFi-systems. However,
    [Show full text]
  • Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
    Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used.
    [Show full text]
  • A New Digital Filter Using Window Resizing for Protective Relay Applications
    A New Digital Filter Using Window Resizing for Protective Relay Applications Bogdan Kasztenny, Mangapathirao V. Mynam, Titiksha Joshi, and Chad Daniels Schweitzer Engineering Laboratories, Inc. Published in the proceedings of the 15th International Conference on Developments in Power System Protection Liverpool, United Kingdom March 9–12, 2020 A NEW DIGITAL FILTER USING WINDOW RESIZING FOR PROTECTIVE RELAY APPLICATIONS Bogdan Kasztenny1*, Mangapathirao V. Mynam1, Titiksha Joshi1, Chad Daniels1 1Schweitzer Engineering Laboratories, Inc., Pullman, Washington, USA *[email protected] Keywords: POWER SYSTEM PROTECTION, VARIABLE-WINDOW FILTER, WINDOW RESIZING. Abstract Digital protective relays use finite impulse response filters with sliding data windows for band-pass filtering of voltages and currents and measurement of phasors. Cosine, Fourier, and Walsh data windows are commonly used. Short windows yield faster protection operation but allow larger transient errors jeopardizing protection security and calling for adequate countermeasures. Often, these countermeasures erase some, if not most, benefits of shorter data windows. This paper presents the theory, implementation, laboratory test results, and a field case example of a new filtering method for protective relaying based on window resizing. The method uses a full-cycle sliding data window until a disturbance is detected, at which time the window size is considerably shortened to include only disturbance samples and exclude all pre-disturbance samples. With passing of time, the window size grows to include more disturbance samples as they become available. When the window reaches its nominal full-cycle size, it stops extending and starts sliding again. By purging the pre-disturbance data, the new filter strikes an excellent balance between speed and accuracy.
    [Show full text]
  • Switched Capacitor Networks and Techniques for the Period 19 1-1992
    Active and Passive Elec. Comp., 1994, Vol. 16, pp. 171-258 Reprints available directly from the publisher Photocopying permitted by license only 1994 Gordon and Breach Science Publishers S.A. Printed in Malaysia A CHRONOLOGICAL LIST OF REFERENCES ON SWITCHED CAPACITOR NETWORKS AND TECHNIQUES FOR THE PERIOD 19 1-1992 A.K. SINGH Electronics Lab., Department of Electronics and Communication Engineering, Delhi Institute of Technology, Kashmere Gate, Delhi 110006, India. (Received November 16, 1993; in final form December 15, 1993) A chronological list of 440 references on switched capacitor (SC) networks from 1939 to May 1981 was published in this Journal by J. Vandewalle. In this communication, we present a compilation of 1357 references covering the period from May 1981-1992 (along with a supplementary list of 43 missing references for the period before May 1981). The present compilation and the earlier one by Vandewalle put together, thus, constitute an exhaustive bibliography of 1797 references on SC-networks and tech- niques till 1992. I. INTRODUCTION The importance of SC-networks in the area of instrumentation and communication is well established. Because of their suitability to VLSI implementation, along with digital networks on the same chip and their low cost coupled with accuracy, SC- networks have greatly enhanced their applicability in the electronics world. Enor- mous volumes of literature on the SC-techniques for different applications is now available. Many design procedures including those based upon immittance simu- lation and wave concepts have been evolved. Application of SC-networks in the design of FIR and IIR filters and neural networks have also been reported.
    [Show full text]
  • Digital Filter Structures from Classical Analogue Networks
    DIGITAL FILTER STRUCTURES FROM CLASSICAL ANALOGUE NETWORKS By STUART SIMON LAWSON A THESIS SUBMITTED FOR THE Ph.D. DEGREE IN THE UNIVERSITY OF LONDON. DEPARTMENT OF ELECTRICAL ENGINEERING, IMPERIAL COLLEGE OF SCIENCE AND TECHNOLOGY, LONDON,S.W.7 OCTOBER 1975- -2- A3STRACT decent investigations have shown that a class of digital filter structures exists that poseeeces mudh lower attenuation distortion than the conventional direct or cascade forms. These structures can be derived from classical analogue doubly- terminated lossless networks by using a one-port wave variable description for circuit elements. The basic teChnique, due to Fettweis, consists of expressing the voltage-current relationship of an element in terms of incident and reflected waves and then applying the bilinear transformation to give the digital equivalent. These digital circuits are then interconnected with the aid of 'Adaptors'. An adaptor is simply the digital realization of Kirchhoff's two laws for a parallel or series junction of n ports. The use of waves in the derivation of the digital filter structures has led to the term ''rave Digital ;Filters' being applied to them. In this thesis it is shown that, by considerinf, each clement in the analogue network as a two-port, a true simulation can be achieved for the corresponding digital filter structure. In the new method, the adaptor, which is needed in the one-port description, is not required explicitly but is included as part of the equivalent wave-flow diagram. The relationship between the sensitivity of the attenuation to first-order multiplier variations and the analogue network element sensitivities is derived and it is shown that the multiplier sensitivities are not generally zero at points of maximum pseudopower transfer.
    [Show full text]
  • All-Analogue Real-Time Broadband Filter Bank Multicarrier Optical Communications System
    > REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < 1 All-Analogue Real-Time Broadband Filter Bank Multicarrier Optical Communications System Fernando A. Gutiérrez, Philip Perry, Member, IEEE, Eamonn P. Martin, Andrew D. Ellis, Member, IEEE, Frank Smyth, Member, IEEE, and Liam P. Barry, Senior Member, IEEE. their optical counterparts. Consequently, wavelength division Abstract— This paper studies the key aspects of an optical link multiplexing (WDM) schemes have been implemented which transmits a broadband microwave filter bank multicarrier employing electrical subsystems in the transmitter and/or the (FBMC) signal. The work is presented in the context of creating receiver, as in coherent WDM [3] or Nyquist WDM [4]. an all-analogue real-time multi-gigabit orthogonal frequency However, to decrease the number of total optical wavelengths, division multiplexing (OFDM) electro-optical transceiver for short range and high capacity data center networks. Passive these systems require broadband baseband signals of tens of microwave filters are used to perform the pulse shaping of the bit Gbaud, which limits its performance and increases the cost streams, allowing an orthogonal transmission without the and difficulty of any practical real-time implementation. necessity of digital signal processing (DSP). Accordingly, a cyclic Subcarrier multiplexing (SCM) is a different alternative that prefix that would cause a reduction in the net data rate is not combines several RF subchannels into one signal, which is required. An experiment consisting of three orthogonally spaced then modulated onto an optical wavelength before 2.7 Gbaud quadrature phase shift keyed (QPSK) subchannels demonstrates that the spectral efficiency of traditional DSP-less transmission over fiber.
    [Show full text]
  • An Overview of Microwave Bandpass Filters with Capacitive Coupled Resonators Siniša P
    December, 2010 Microwave Review An Overview of Microwave Bandpass Filters with Capacitive Coupled Resonators Siniša P. Jovanović Abstract – This paper presents a summary of several bandpass Resonators within a filter can be mutually coupled by filters all consisting of resonators coupled only by capacitive capacitive (electric) coupling (Fig. 1a), inductive (magnetic) coupling. The basic filter’s configuration with asymmetric inductors coupling (Fig. 1b) or mixed coupling (Fig. 1c) [7]. Higher- is explained in detail as well as its modifications with asymmetric order filters usually employ all these coupling types to achieve capacitors. The filter’s design process is undemanding due to the desired characteristics. However, as shown in [8-16] it is filter’s simple configuration, while its compact size makes it suitable for integration. Six filters with central frequencies ranging from possible to realize filters made with only capacitive coupling UHF to X band were designed, realized, and tested with excellent resonators which occupy a significantly smaller area agreement between the predicted and measured results. compared to filters with inductive or mixed coupling. Keywords – Capacitive coupling, lattice structure, bandpass filters, microstrip, printed filters. II. FILTER’S CONFIGURATION I. INTRODUCTION Fig. 2 shows a basic electric scheme of a filter that consists of four identical resonators (Q1 to Q4) electrically coupled by Band pass filters with low insertion losses are essential capacitors Cr. Although the scheme has only four variables, components of all kinds of modern communication devices Cp, Cr, L1, and L2, by varying their values it is possible to because of both their band selecting and image and spurious obtain a band pass filter at a desired central frequency.
    [Show full text]
  • A Review and Modern Approach to LC Ladder Synthesis
    J. Low Power Electron. Appl. 2011, 1, 20-44; doi:10.3390/jlpea1010020 OPEN ACCESS Journal of Low Power Electronics and Applications ISSN 2079-9268 www.mdpi.com/journal/jlpea Review A Review and Modern Approach to LC Ladder Synthesis Alexander J. Casson ? and Esther Rodriguez-Villegas Circuits and Systems Research Group, Electrical and Electronic Engineering Department, Imperial College London, SW7 2AZ, UK; E-Mail: [email protected] ? Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +44(0)20-7594-6297; Fax: +44(0)20-7581-4419. Received: 19 November 2010; in revised form: 14 January 2011 / Accepted: 22 January 2011 / Published: 28 January 2011 Abstract: Ultra low power circuits require robust and reliable operation despite the unavoidable use of low currents and the weak inversion transistor operation region. For analogue domain filtering doubly terminated LC ladder based filter topologies are thus highly desirable as they have very low sensitivities to component values: non-exact component values have a minimal effect on the realised transfer function. However, not all transfer functions are suitable for implementation via a LC ladder prototype, and even when the transfer function is suitable the synthesis procedure is not trivial. The modern circuit designer can thus benefit from an updated treatment of this synthesis procedure. This paper presents a methodology for the design of doubly terminated LC ladder structures making use of the symbolic maths engines in programs such as MATLAB and MAPLE. The methodology is explained through the detailed synthesis of an example 7th order bandpass filter transfer function for use in electroencephalogram (EEG) analysis.
    [Show full text]
  • Applied Signal Processing
    APPLIED SIGNAL PROCESSING 2004 Chapter 1 Digital ¯ltering In this section digital ¯lters are discussed, with a focus on IIR (In¯nite Impulse Re- sponse) ¯lters and their applications. The most important kinds of IIR ¯lter prototypes are discussed in section 1.1, and structures used in the implementation of IIR ¯lters are presented in section 1.2. In section 1.3 some important ¯lters designed for special purposes are discussed. Finally, the application of digital ¯ltering will be illustrated in section 1.4 by two case studies: ² Dual-tone multifrequency (DTMF) generation and detection in digital telephony, and ² Plucked-string ¯lters in synthetic music. 1.1 IIR ¯lter prototypes An IIR ¯lter of order N is described by the di®erence equation y(n) + a1y(n ¡ 1) + ¢ ¢ ¢ + aN y(n ¡ N) = b0x(n) + b1x(n ¡ 1) + ¢ ¢ ¢ + bM x(n ¡ M) (1.1) and it has the transfer function N N¡1 N¡M b0z + b1z + ¢ ¢ ¢ + bM z H(z) = N N¡1 (1.2) z + a1z + ¢ ¢ ¢ + aN IIR ¯lters provide more flexibility than FIR ¯lters due to the feedback from previous outputs. Compared to FIR ¯lters, the denominator polynomial of H(z) provides more freedom to shape the frequency response of the ¯lter. Therefore an IIR ¯lter which achieves a given set of speci¯cations is usually simpler and has much fewer parameters than a FIR ¯lters designed for the same speci¯cations. This property makes IIR ¯lters well suited for a number of applications. On the other hand, IIR ¯lters have some limitations which one should be aware of.
    [Show full text]