Model Behavior: the Evolving Use of Physical Prototypes in Structural Shell Design, 1959-1974
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Frei Ottoâ•Žs Pneumatic Experiments for Humanitarian Design
Architecture Conference Proceedings and Presentations Architecture 6-2021 Frei Otto’s Pneumatic Experiments for Humanitarian Design Rob Whitehead Iowa State University, [email protected] Follow this and additional works at: https://lib.dr.iastate.edu/arch_conf Part of the Architectural Technology Commons, Cultural Resource Management and Policy Analysis Commons, Environmental Design Commons, and the Historic Preservation and Conservation Commons Recommended Citation Whitehead, Rob, "Frei Otto’s Pneumatic Experiments for Humanitarian Design" (2021). Architecture Conference Proceedings and Presentations. 145. https://lib.dr.iastate.edu/arch_conf/145 This Conference Proceeding is brought to you for free and open access by the Architecture at Iowa State University Digital Repository. It has been accepted for inclusion in Architecture Conference Proceedings and Presentations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Frei Otto’s Pneumatic Experiments for Humanitarian Design Abstract This paper will explore the intersection of building technology and humanitarian design-science research by looking at Frei Otto’s pneumatic experiments. The purpose of the study is to contextualize our contemporary demands for humanitarian design work by reflecting upon the manner by which Otto integrated an ambitious design ideology with an elevated and innovative technical acumen. Constraining the investigation to Otto’s work, particularly his relatively unknown early -

Lightweight Landscape Enhancing Design Through Minimal Mass Structures
SPRINGER BRIEFS IN APPLIED SCIENCES AND TECHNOLOGY POLIMI SPRINGER BRIEFS Alessandra Zanelli Luigi Spinelli Carol Monticelli Paolo Pedrali Editors Lightweight Landscape Enhancing Design through Minimal Mass Structures 123 SpringerBriefs in Applied Sciences and Technology PoliMI SpringerBriefs Editorial Board Barbara Pernici, Politecnico di Milano, Milano, Italy Stefano Della Torre, Politecnico di Milano, Milano, Italy Bianca M. Colosimo, Politecnico di Milano, Milano, Italy Tiziano Faravelli, Politecnico di Milano, Milano, Italy Roberto Paolucci, Politecnico di Milano, Milano, Italy Silvia Piardi, Politecnico di Milano, Milano, Italy [email protected] More information about this series at http://www.springer.com/series/11159 http://www.polimi.it [email protected] Alessandra Zanelli • Luigi Spinelli Carol Monticelli • Paolo Pedrali Editors Lightweight Landscape Enhancing Design through Minimal Mass Structures 123 [email protected] Editors Alessandra Zanelli Carol Monticelli Department of ABC Department of ABC Politecnico di Milano Politecnico di Milano Milan Milan Italy Italy Luigi Spinelli Paolo Pedrali Department of DAStU Department of DAStU Politecnico di Milano Politecnico di Milano Milan Milan Italy Italy ISSN 2191-530X ISSN 2191-5318 (electronic) SpringerBriefs in Applied Sciences and Technology ISSN 2282-2577 ISSN 2282-2585 (electronic) PoliMI SpringerBriefs ISBN 978-3-319-21664-5 ISBN 978-3-319-21665-2 (eBook) DOI 10.1007/978-3-319-21665-2 Library of Congress Control Number: 2015949477 Springer Cham Heidelberg New York Dordrecht London © The Author(s) 2016 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. -

Venice & the Common Ground
COVER Magazine No 02 Venice & the Common Ground Magazine No 02 | Venice & the Common Ground | Page 01 TABLE OF CONTENTS Part 01 of 02 EDITORIAL 04 STATEMENTS 25 - 29 EDITORIAL Re: COMMON GROUND Reflections and reactions on the main exhibition By Pedro Gadanho, Steven Holl, Andres Lepik, Beatrice Galilee a.o. VIDEO INTERVIew 06 REPORT 30 - 31 WHAT IS »COMMON GROUND«? THE GOLDEN LIONS David Chipperfield on his curatorial concept Who won what and why Text: Florian Heilmeyer Text: Jessica Bridger PHOTO ESSAY 07 - 21 INTERVIew 32 - 39 EXCAVATING THE COMMON GROUND STIMULATORS AND MODERATORS Our highlights from the two main exhibitions Jury member Kristin Feireiss about this year’s awards Interview: Florian Heilmeyer ESSAY 22 - 24 REVIEW 40 - 41 ARCHITECTURE OBSERVES ITSELF GUERILLA URBANISM David Chipperfield’s Biennale misses social and From ad-hoc to DIY in the US Pavilion political topics – and voices from outside Europe Text: Jessica Bridger Text: Florian Heilmeyer Magazine No 02 | Venice & the Common Ground | Page 02 TABLE OF CONTENTS Part 02 of 02 ReVIEW 42 REVIEW 51 REDUCE REUSE RECYCLE AND NOW THE ENSEMBLE!!! Germany’s Pavilion dwells in re-uses the existing On Melancholy in the Swiss Pavilion Text: Rob Wilson Text: Rob Wilson ESSAY 43 - 46 ReVIEW 52 - 54 OLD BUILDINGS, New LIFE THE WAY OF ENTHUSIASTS On the theme of re-use and renovation across the An exhibition that’s worth the boat ride biennale Text: Elvia Wilk Text: Rob Wilson ReVIEW 47 ESSAY 55 - 60 CULTURE UNDER CONSTRUCTION DARK SIDE CLUB 2012 Mexico’s church pavilion The Dark Side of Debate Text: Rob Wilson Text: Norman Kietzman ESSAY 48 - 50 NEXT 61 ARCHITECTURE, WITH LOVE MANUELLE GAUTRAND Greece and Spain address economic turmoil Text: Jessica Bridger Magazine No 02 | Venice & the Common Ground | Page 03 EDITORIAL Inside uncube No.2 you’ll find our selections from the 13th Architecture Biennale in Venice. -

Anything Goes? Berlin Architecture in the 1980S 1 7.3
Press Kit Berlin, 17.3.21 , Foto: © Unbekannte*r Fotograf*in / Berlinische Galerie, Digitalisierung: Anja Elisabeth Witte 1984 Manfred Prasser, Dieter Bankert, Walter Schwarz, Friedrichstadtpalast, kurzJahr nach seiner Eröffnung im Anything Goes? Berlin Architecture in the 1980s 1 7.3. – 16.8.21 C ontents P ress release Anything Goes? P. 1 Press release Revisited P. 3 Press release Tactile models P. 4 Press release Audiowalks P. 6 I nvolved Artists and Architects P. 7 E xhibitions texts P. 8 Handout Video programme P. 11 C atalogue P. 13 P ress images P. 14 Co ntact P. 18 Press Release Berlin, 17.3.21 Berlin boasts a unique concentration of notewor- thy buildings from the 1980s, and more than 30 years , later they deserve a review. The colourful diversity 1984 of this architectural vocabulary challenged previous ideas of living in the modern world. Widely labelled “postmodern”, it drew on structural typologies and stylistic devices from the past and tested alterna- tive urban lifestyles. In the run-up to the celebrations marking 750 years since the original town charter, the entries submitted to the “Internationale Bauausstel- lung” in West Berlin in 1984/87 and the “Bauausstel- lung” of 1987 in East Berlin turned the city into a kind of architectural laboratory observed from well beyond its boundaries. Even at the design stage, some were already attracting criticism as artistically misguided, and significant examples of this era in architecture have since disappeared, been revamped or else threatened by demolition. By around three hundred prints, mod- els, photographs, paintings, films, and tactile models, the exhibition examines for the first time the build- ings and visions in East and West Berlin that were developed in the final decade before the fall of the Manfred Prasser, Dieter Bankert, Walter Schwarz, Friedrichstadtpalast, kurz nach seiner Eröffnung im Jahr Foto: © Unbekannte*r Fotograf*in / Berlinische Galerie, Digitalisierung: Anja Elisabeth Witte Berlin Wall. -

The Tragedy of the Megastructure
105 Megastructures 3 | 2018 | 1 The Tragedy of the Megastructure Valentin Bourdon PhD Candidate École Polytechnique Fédérale de Lausanne [email protected] Valentin Bourdon is a PhD student at the Laboratory of Construction and Conservation (LCC) EPFL since 2017. His research explores the architectural challenges of the common space. In support of significant historical experiences, and contemporary subjects, such a project aims to help overcome the delay taken by architecture comparing to other disciplines in the appropriation of the notion of ‘common’. ABSTRACT Relating the megastructure to the issue of the commons is a useful exercise to understand the success and the disappearance of what Peter Reyner Banham called the “dinosaurs of the Modern Movement”. All these large-scale constructions suffered the same fate: a conflict between the promise of a large shared space and the temptation of its fragmentation. This quantitative quandary is also raised in another field by Garrett Hardin in 1968 as the ‘enclosure dilemma’. The publication of his article “The Tragedy of the Commons” sparked a broad controversy coinciding with the megastructure’s momentum. By assessing a number of theoretical correspondences, the article reexamines the impact of megastructures on the interdisciplinary debates of the time. It also considers the relationship between architecture and property as one of the possible–and tragically coincident–reasons for their success and dissolution. https://doi.org/10.6092/issn.2611-0075/8523 ISSN 2611-0075 Copyright © 2018 Valentin Bourdon 4.0 KEYWORDS Megastructure; Commons; Ownership; Enclosure; Anti-enclosure. Valentin Bourdon The Tragedy of the Megastructure 106 When the American ecologist Garrett Hardin publishes his famous article entitled “The Tragedy of the Commons”1 in Science, the architectural 1. -

A Research on a Reconfigurable Hypar Structure for Architectural Applications
A RESEARCH ON A RECONFIGURABLE HYPAR STRUCTURE FOR ARCHITECTURAL APPLICATIONS A Thesis Submitted to the Graduate School of Engineering and Sciences of İzmir Institute of Technology in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE in Architecture by Gözde SUSAM December 2013 İZMİR We approve the thesis of Gözde SUSAM Examining Committee Members: Assoc. Prof. Dr. Koray KORKMAZ Department of Architecture, Izmir Institute of Technology Assist. Prof. Dr. Gökhan KİPER Department of Mechanical Engineering, Izmir Institute of Technology Assist. Prof. Dr. A. Vefa ORHON Department of Architecture, Dokuz Eylül University 20 December 2013 Assoc. Prof. Dr. Koray KORKMAZ Supervisor, Department of Architecture Izmir Institute of Technology Assoc. Prof. Dr. Şeniz ÇIKIŞ Prof. Dr. R. Tuğrul SENGER Head of the Department of Architecture Dean of the Graduate School of Engineering and Sciences ACKNOWLEDGMENTS I would like to express my special thanks to my supervisor Assoc. Prof. Dr. Koray Korkmaz for his guidance and support throughout my research. Secondly, I would like to thank other members of the examining committee; Assist. Prof. Dr. Gökhan Kiper and Assist. Prof. Dr. A. Vefa Orhon, for their valuable suggestions and comments. I’m eternally grateful to my family for their morally and aptly contributions and moreover being a part of my life. ABSTRACT A RESEARCH ON A RECONFIGURABLE HYPAR STRUCTURE FOR ARCHITECTURAL APPLICATIONS Kinetic design strategy is a way to obtain remarkable applications in architecture. These kinetic designs can offer more advantages compared to conventional ones. Basic knowledge of different disciplines is necessary to generate kinetic designs. In other words, interdisciplinary studies are critical. -

Frei Otto 2015 Laureate Media Kit
Frei Otto 2015 Laureate Media Kit For more information, please visit pritzkerprize.com. © 2015 The Hyatt Foundation Contents Contact Media Release ................................ 2 Tributes to Frei Otto ............................ 4 Edward Lifson Jury Citation .................................. 9 Director of Communications Jury Members .................................10 Pritzker Architecture Prize Biography ....................................11 [email protected] Past Laureates .................................14 +1 312 919 1312 About the Medal ...............................17 History of the Prize .............................18 Evolution of the Jury. .19 Ceremonies Through the Years ................... 20 2015 Pritzker Architecture Prize Media Kit Media Release Announcing the 2015 Laureate Frei Otto Receives the 2015 Pritzker Architecture Prize Visionary architect, 89, dies in his native Germany on March 9, 2015 Otto was an architect, visionary, utopian, ecologist, pioneer of lightweight materials, protector of natural resources and a generous collaborator with architects, engineers, and biologists, among others. Chicago, IL (March 23, 2015) — Frei Otto has received the 2015 Pritzker Architecture Prize, Tom Pritzker announced today. Mr. Pritzker is Chairman and President of The Hyatt Foundation, which sponsors the prize. Mr. Pritzker said: “Our jury was clear that, in their view, Frei Otto’s career is a model for generations of architects and his influence will continue to be felt. The news of his passing is very sad, unprecedented in the history of the prize. We are grateful that the jury awarded him the prize while he was alive. Fortunately, after the jury decision, representatives of the prize traveled to Mr. Otto’s home and were able to meet with Mr. Otto to share the news with him. At this year’s Pritzker Prize award ceremony in Miami on May 15 we will celebrate his life and timeless work.” Mr. -

Downloads/2003 Essay.Pdf, Accessed November 2012
UCLA UCLA Electronic Theses and Dissertations Title Nation Building in Kuwait 1961–1991 Permalink https://escholarship.org/uc/item/91b0909n Author Alomaim, Anas Publication Date 2016 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA Los Angeles Nation Building in Kuwait 1961–1991 A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Architecture by Anas Alomaim 2016 © Copyright by Anas Alomaim 2016 ABSTRACT OF THE DISSERTATION Nation Building in Kuwait 1961–1991 by Anas Alomaim Doctor of Philosophy in Architecture University of California, Los Angeles, 2016 Professor Sylvia Lavin, Chair Kuwait started the process of its nation building just few years prior to signing the independence agreement from the British mandate in 1961. Establishing Kuwait’s as modern, democratic, and independent nation, paradoxically, depended on a network of international organizations, foreign consultants, and world-renowned architects to build a series of architectural projects with a hybrid of local and foreign forms and functions to produce a convincing image of Kuwait national autonomy. Kuwait nationalism relied on architecture’s ability, as an art medium, to produce a seamless image of Kuwait as a modern country and led to citing it as one of the most democratic states in the Middle East. The construction of all major projects of Kuwait’s nation building followed a similar path; for example, all mashare’e kubra [major projects] of the state that started early 1960s included particular geometries, monumental forms, and symbolic elements inspired by the vernacular life of Kuwait to establish its legitimacy. -

The Art of Architecture/ the Politics of Awards: 2016 Pritzker Architecture Prize Continues Conversations About Sexism and Social Value
MARCH // APRIL // 2016 DIVERSITY IN THE PROFESSION ON THE RISE, AIDED BY NEW INITIATIVES // 34 THE PRITZKER PRIZE // 42 M A RAIACHICAGO.ORG C H // A PR I L // 2 016 1 THE ART OF ARCHITECTURE/ THE POLITICS OF AWARDS: 2016 PRITZKER ARCHITECTURE PRIZE CONTINUES CONVERSATIONS ABOUT SEXISM AND SOCIAL VALUE BY DAWN REISS Students romp and play in the Obama Library Drone Aviary 42 MARCH // APRIL // 2016 CHICAGO ARCHITECT AIACHICAGO.ORG 2016 PRITZKER ARCHITECTURE PRIZE CONTINUES CONVERSATIONS ABOUT SEXISM AND SOCIAL VALUE artha Thorne, executive director of the Pritzker Architecture Prize vividly remembers the phone call she made to Alejandro Aravena telling him the eight-person jury Mhad selected him as the 2016 prizewinner. “He literally could not speak,” Thorne said. “The first thing he said to me was ‘Martha, don’t joke about these things.’ I said ‘But I’m not.’” Thorne says the Chilean architect, who is the direc- tor of the 2016 Venice Architecture Biennale, was genuinely shocked and emotional. “He never expected it,” Thorne said. “In part because he is that type of person, incredibly generous. The jury is committed to the prize and the best. They are committed to the mission of the prize before any other. There’s no benefit for the jury in engaging in politics.” But as anyone knows, anytime there’s a group of people, there are politics. Since the inception of the Pritzker Architecture Prize by Jay and Cindy Pritzker, which was first given to Phillip Johnson in 1979, the influential prize has been synonymous as the “Nobel Prize for architects.” There’s no doubt that the winners are some of most influential architects from I. -
Understanding Western Architecture
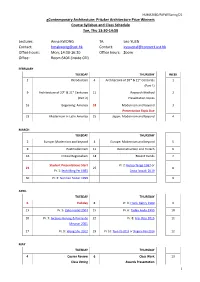
HUMA3680/PAPW/Spring/21 gContemporary Architecture: Pritzker Architecture Prize Winners Course Syllabus and Class Schedule Tue, Thu 13:30-14:50 Lecturer: Anna KWONG TA: Leo YUEN Contact: [email protected] Contact: [email protected] Office hours: Mon, 14:30-16:30 Office hours: Zoom Office: Room 6404 (inside CEI) FEBRUARY TUESDAY THURSDAY WEEK 2 Introduction 4 Architecture of 20th & 21st Centuries 1 (Part 1) 9 Architecture of 20th & 21st Centuries 11 Research Method 2 (Part 2) Presentation Topics 16 Beginning: America 18 Modernism and beyond 3 Presentation Topic Due 23 Modernism in Latin America 25 Japan: Modernism and beyond 4 MARCH TUESDAY THURSDAY 2 Europe: Modernism and beyond 4 Europe: Modernism and beyond 5 9 Postmodernism 11 Deconstruction and Hi-tech 6 16 Critical Regionalism 18 Recent trends 7 Student Presentations Start Pr. 2: Kenzo Tange 1987 or 23 25 8 Pr. 1: Ieoh Ming Pei 1983 Arata Isozaki 2019 30 Pr. 3: Norman Foster 1999 9 APRIL TUESDAY THURSDAY 6 Holiday 8 Pr. 4: Frank Gehry 1989 9 13 Pr. 5: Zaha Hadid 2004 15 Pr. 6: Tadao Ando 1995 10 20 Pr. 7: Jacques Herzog & Pierre de 22 Pr. 8: Frei Otto 2015 11 Meuron 2001 27 Pr. 9: Wang Shu 2012 29 Pr. 10: Toyo Ito 2013 or Shigeru Ban 2014 12 MAY TUESDAY THURSDAY 4 Course Review 6 Class Work 13 Class Voting Awards Presentation 1 HUMA3680/PAPW/Spring/21 Course Structure The first half of the course will review the background of the Pritzker Architecture Prize and some Pritzker Prize winners will be presented. -

1 Stuttgart Zurich
BUILDINGS TO BE VISITED Contemporary le corbusier Stuttgart Weissenhofsiedlung Houses 13,14 &15 Landesgartenschau Exhibition Hall, 2014 Prof. A. Menges, Tobias Schwinn, J. Knippers + Institute for Computational Design / Institute for Lightweight Structures, 2014 Prof. A. Menges, Jan Knippers Institute of Lightweight Structure Building, 1964 Frei Otto Killesberg Park Tower, 2000 Schlaich, Bergerman and Partners Stuttgart City Library, 2011 Yi Architects Neue Staatsgalerie, 198 James Stirling + Partners Mercedes Benz Museum, 2006 UNStudio Porsche Museum, 2009 Delugan Meissel Centre for Virtual Engineering, 2012 UNStudio Kunstmuseum, 2005 Hascher Jehle Architektur Deportation Memorial at North Station, 2006 R128 House, 1998 Roemerstrasse 128 Werner Sobek Zurich Heidi weber museum University of Zurich Law Library, 2004 Santiago Calatrava University of Zurich / Museum of Natural History, 1926, 2002 Karl Moser, Lecture Hall, Gigon & Guyer ETH Library and Exhibition Hall, 1864 Gustav Zeuner focusTerra, Natural Science Institute, 2009 Holzer Kobler 1 Campus Careum, University of Zurich, 2011 GWJ Architektur Bahnhof Stadelhofen, 1984 Santiago Calatrava Kunsthaus / Kunsthaus Addition, 2012 David Chipperfield Bahnhof Enge, 1927 Otto and Werner Pfister Tamedia Office Building, 2013 Shigeru Ban Allianz Headquarters, 2013 Wiel Arets Architecture Dynamo Metal Workshop, 2008 Phalt Architekten Dolder Grand, 2008 Foster and Partners Freitag Store, 2006 Spillman Eschle Architekten Hallenbad Swimmimg Pool, 1938 Sihlholzi Sports Center & Band Stand, 1929 Robert -

Lecture Handouts, 2013
Arch. 48-350 -- Postwar Modern Architecture, S’13 Prof. Gutschow, Classs #1 INTRODUCTION & OVERVIEW Introductions Expectations Textbooks Assignments Electronic reserves Research Project Sources History-Theory-Criticism Methods & questions of Architectural History Assignments: Initial Paper Topic form Arch. 48-350 -- Postwar Modern Architecture, S’13 Prof. Gutschow, Classs #2 ARCHITECTURE OF WWII The World at War (1939-45) Nazi War Machine - Rearming Germany after WWI Albert Speer, Hitler’s architect & responsible for Nazi armaments Autobahn & Volkswagen Air-raid Bunkers, the “Atlantic Wall”, “Sigfried Line”, by Fritz Todt, 1941ff Concentration Camps, Labor Camps, POW Camps Luftwaffe Industrial Research London Blitz, 1940-41 by Germany Bombing of Japan, 1944-45 by US Bombing of Germany, 1941-45 by Allies Europe after WWII: Reconstruction, Memory, the “Blank Slate” The American Scene: Pearl Harbor, Dec. 7, 1941 Pentagon, by Berman, DC, 1941-43 “German Village,” Utah, planned by US Army & Erich Mendelsohn Military production in Los Angeles, Pittsburgh, Detroit, Akron, Cleveland, Gary, KC, etc. Albert Kahn, Detroit, “Producer of Production Lines” * Willow Run B-24 Bomber Plant (Ford; then Kaiser Autos, now GM), Ypsilanti, MI, 1941 Oak Ridge, TN, K-25 uranium enrichment factory; town by S.O.M., 1943 Midwest City, OK, near Midwest Airfield, laid out by Seward Mott, Fed. Housing Authortiy, 1942ff Wartime Housing by Vernon Demars, Louis Kahn, Oscar Stonorov, William Wurster, Richard Neutra, Walter Gropius, Skidmore-Owings-Merrill, et al * Aluminum Terrace, Gropius, Natrona Heights, PA, 1941 Women’s role in the war production, “Rosie the Riverter” War time production transitions to peacetime: new materials, new design, new products Plywod Splint, Charles Eames, 1941 / Saran Wrap / Fiberglass, etc.