DOCSLIB.ORG

Time Series Analysis: 4. Linear Filters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Time Series Analysis: 4. Linear Filters Time Series Analysis: 4. Linear filters P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Linear filters in the Fourier domain Filtering: Multiplying the transform by a transfer function. gn −! Gn −! H(fn)Gn −! ~gn (1) DFT inverse DFT where H(fn) is the transfer function discretized over fn. The most important drawback: You need to know the whole series, collect all data, prior to filtering. Copyright c 2009-12 P. F. Góra 4–2 Example 1 8 <1 jfj 6 fc 0.8 H(f) = :0 jfj > fc 0.6 4 H(f) 2 exp −(f=fc) H(f) = 4 0.4 1 + exp −(f=fc) 0.2 0 0 1 2 3 4 f Copyright c 2009-12 P. F. Góra 4–3 2 1 0 -1 -2 4 6 8 10 12 14 16 18 2 1 0 -1 -2 4 6 8 10 12 14 16 18 2 1 0 -1 -2 4 6 The signal8 before10 and12 after filtering14 16 18 Copyright c 2009-12 P. F. Góra 4–4 A reason for the strange result of the “blue” filtering 2 1 0 -1 -2 4 6 8 10 12 14 16 18 When filtering in the Fourier domain, we usually do not smooth out the filters. Copyright c 2009-12 P. F. Góra 4–5 Linear filters Filtering in Fourier domain is very easy: multiply the DFT of the input by the transfer function. Filtering in the signal domain can be tricky: a FIR filter: x(t) y(t) r(t) an IIR filter: x(t) y(t) r(t) Copyright c 2009-12 P. F. Góra 4–6 The transfer function Even though the filters are realized in the signal domain, it is convenient to ana- lyse them in Fourier domain. Every possible linear filter is represented by Y (f) = H(f)X(f) : (2) H(f) is the transfer function. Copyright c 2009-12 P. F. Góra 4–7 Terminology •H (f) = 0 for jfj > f0 — a low-pass filter. •H (f) = 0 for jfj 6 f0 — a high-pass filter. •H (f) 6= 0 for f1 6 jfj 6 f2 — a band-pass filter. •H (f) = 0 for f1 6 jfj 6 f2 — a band-stop filter; if f2 − f1 is small, also known as a notch filter. Copyright c 2009-12 P. F. Góra 4–8 A general linear filter in the signal domain has the form q p X X yn = αkxn−k + βkyn−k (3) k=−s k=1 xn is a (discretized) input signal, yn is the output signal. If s > 0, future values of the input are needed to construct the output. Such filter is non-causal. It cannot be realized on-line (or in real time). Copyright c 2009-12 P. F. Góra 4–9 Eq. (3): q p X X yn = αkxn−k + βkyn−k k=−s k=1 • If p = 0, the filter is a Finite Impulse Response filter (FIR), or a moving average filter. The output of such a filter dies out in a finite time after the input has died out. • If p > 0, the filter is Infinite Impulse Response filter (IIR), or an autoregres- sive filter. Its output can go on infinitely long after the input has died out (in fact, this is a parasitic behaviour). Copyright c 2009-12 P. F. Góra 4–10 Causal FIR filters q X yn = αkxn−k : (4) k=0 If the input is stationary, the output also is. q is called the order of the filter. Copyright c 2009-12 P. F. Góra 4–11 To find the transfer function, we Fourier transform Eq. (4). N−1 N−1 q 1 X 2πimn=N 1 X 2πimn=N X Ym = p e yn = p e αkxn−k N n=0 N n=0 k=0 q N−1 q N−1−k X 1 X 2πimn=N X 1 X 2πim(n0+k)=N = αkp e xn−k = αkp e xn0 : k=0 N n=0 k=0 N n0=−k (5) Copyright c 2009-12 P. F. Góra 4–12 By the assumption of periodicity of the input, x−l ≡ xN−l. On the other hand, exp(2πim(N−l)=N)= exp(2πim) exp(2πim(−l)=N)= exp(2πim(−l)=N). Thus q N−1 q X 2πimk=N 1 X 2πimn0=N X 2πimk=N Ym = αke p e xn0 = αke Xm : (6) k=0 N n0=0 k=0 | {z } | {z } Xm Hm m=N = m=(N∆) ∆ = fm∆, where fm is the m-th discrete Fourier frequency. Therefore. Copyright c 2009-12 P. F. Góra 4–13 Transfer function of a causal FIR filter has the form q k X 2πifm∆ 2πifm∆ H(fm) = αk e = α e ; (7) k=0 where α(z) is the following polynomial of order q q X k α(z) = αkz (8) k=0 (coefficients of the filter become coefficients of the polynomial (8)). Usually, for the sake of simplicity, we assume that ∆ = 1, or that the sam- pling time is the time unit. Remember: With this notation, frequencies become dimensionless and the Nyquist interval equals [−1=2; 1=2]. Copyright c 2009-12 P. F. Góra 4–14 Transfer function of a general FIR filter The above can be easily generalized to arbitrary (non-causal) FIR filters. The transfer function becomes q k X 2πifm∆ 2πifm∆ H(fm) = αk e = α e ; (9) k=−s where α(·) is now an appropriate rational function. Copyright c 2009-12 P. F. Góra 4–15 Simple low- and high-pass filters Consider a filter 1 1 1 y = x + x + x : (10) n 4 n−1 2 n 4 n+1 Its transfer function reads 1 2πif 1 1 −2πif 1 1 2 Hc(f) = e + + e = + cos 2πf = cos πf : (11) 4 2 4 2 2 Similarly, the transfer function of the filter 1 1 1 y = − x + x − x : (12) n 4 n−1 2 n 4 n+1 reads 1 2πif 1 1 −2πif 1 1 2 Hs(f) = − e + − e = − cos 2πf = sin πf : (13) 4 2 4 2 2 Copyright c 2009-12 P. F. Góra 4–16 (10) is a (poor) low-pass filter. (12) is a (poor) high-pass filter. 1 1 0.75 0.75 f f π π 2 0.5 2 0.5 sin cos 0.25 0.25 0 0 -0.5 -0.25 0 0.25 0.5 -0.5 -0.25 0 0.25 0.5 f f Copyright c 2009-12 P. F. Góra 4–17 The “usual” moving average The (unweighted) moving average 1 y = x + x + ··· + x + ··· + x + x ; (14) n 2l + 1 n−l n−l+1 n n+l−1 n+l with the transfer function 1 H (f) = (1 + 2 cos 2πf + 2 cos 4πf + ··· + 2 cos 2lπf) (15) MA 2l + 1 is a poor low-pass filter. Copyright c 2009-12 P. F. Góra 4–18 Transfer functions of unweighted moving averages 1 l=1 l=2 l=3 l=5 0.75 (f)| 0.5 MA |H 0.25 0 -0.5 -0.25 0 0.25 0.5 f Copyright c 2009-12 P. F. Góra 4–19 An example of the usual moving average (the noise of the order of the signal) l= 0 l= 1 Moving Averages l= 5 l=16 Copyright c 2009-12 P. F. Góra 4–20 Differentiating filters First derivative: dg 1 g(x) − g(x − ∆) g(x + ∆) − g(x) 1 1 ' + = g(x + ∆) − g(x − ∆) (16a) dx x 2 ∆ ∆ 2∆ 2∆ 1 1 y = x − x 1 (16b) n 2∆ n+1 2∆ n− i H(f) = sin(2πf∆) (16c) ∆ Second derivative: 1 1 1 y = x − x + x 1 (17a) n 4∆2 n+1 2∆2 n 4∆2 n− 1 H(f) = − sin(πf∆) (17b) ∆2 Copyright c 2009-12 P. F. Góra 4–21 2.5 2.0 1.5 1.0 n y 0.5 0.0 -0.5 -1.0 -1.5 0 5 10 15 20 25 30 n Copyright c 2009-12 P. F. Góra 4–22 2.0 1.5 1.0 0.5 n y 0.0 -0.5 -1.0 -1.5 -2.0 0 5 10 15 20 25 30 n Copyright c 2009-12 P. F. Góra 4–23 Phase of the transfer function In Fourier domain, Y (f) = H(f)X(f) : (18) iφ(f) H(f) = R(f)e , R(f) > 0. The modulus of the transfer function ampli- fies/reduces contributions from the corresponding frequencies. What does the phase, φ(f), do? Copyright c 2009-12 P. F. Góra 4–24 The filter (10) is non-causal, but it is easy to find its causal version: we need to introduce a time delay: 1 1 1 y = x + x + x (19) n 4 n−2 2 n−1 4 n with the transfer function H(f) = e2πif cos2 πf : (20) This transfer function differs from that of (10) only by a phase factor. The phase factor in (20) is responsible for the time delay! Copyright c 2009-12 P. F. Góra 4–25 Suppose that the phase of the transfer function depends linearly on frequencies, φ(f) = af∆. Calculate the inverse transform: X −2πifnk∆ X iafn∆ −2πifnk∆ yk(t) ∼ H(fn)X(fn)e = R(fn)e X(fn)e n n X −2πif (k−a)∆ = R(fn)X(fn)e n ; (21) n which corresponds to a time shift of a units (“channels”).
Load more

Recommended publications
  • Emotion Perception and Recognition: an Exploration of Cultural Differences and Similarities
    Emotion Perception and Recognition: An Exploration of Cultural Differences and Similarities Vladimir Kurbalija Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Mirjana Ivanović Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Miloš Radovanović Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Zoltan Geler Department of Media Studies, Faculty of Philosophy, University of Novi Sad dr Zorana Đinđića 2, 21000 Novi Sad, Serbia +381 21 4853918, [email protected] Weihui Dai School of Management, Fudan University Shanghai 200433, China [email protected] Weidong Zhao School of Software, Fudan University Shanghai 200433, China [email protected] Corresponding author: Vladimir Kurbalija, tel. +381 64 1810104 ABSTRACT The electroencephalogram (EEG) is a powerful method for investigation of different cognitive processes. Recently, EEG analysis became very popular and important, with classification of these signals standing out as one of the mostly used methodologies. Emotion recognition is one of the most challenging tasks in EEG analysis since not much is known about the representation of different emotions in EEG signals. In addition, inducing of desired emotion is by itself difficult, since various individuals react differently to external stimuli (audio, video, etc.). In this article, we explore the task of emotion recognition from EEG signals using distance-based time-series classification techniques, involving different individuals exposed to audio stimuli.
    [Show full text]
  • Lecture 3: Transfer Function and Dynamic Response Analysis
    Transfer function approach Dynamic response Summary Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis Paweł Malczyk Division of Theory of Machines and Robots Institute of Aeronautics and Applied Mechanics Faculty of Power and Aeronautical Engineering Warsaw University of Technology October 17, 2019 © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 1 / 31 Transfer function approach Dynamic response Summary Outline 1 Transfer function approach 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 2 / 31 Transfer function approach Dynamic response Summary Transfer function approach 1 Transfer function approach SISO system Definition Poles and zeros Transfer function for multivariable system Properties 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 3 / 31 Transfer function approach Dynamic response Summary SISO system Fig. 1: Block diagram of a single input single output (SISO) system Consider the continuous, linear time-invariant (LTI) system defined by linear constant coefficient ordinary differential equation (LCCODE): dny dn−1y + − + ··· + _ + = an n an 1 n−1 a1y a0y dt dt (1) dmu dm−1u = b + b − + ··· + b u_ + b u m dtm m 1 dtm−1 1 0 initial conditions y(0), y_(0),..., y(n−1)(0), and u(0),..., u(m−1)(0) given, u(t) – input signal, y(t) – output signal, ai – real constants for i = 1, ··· , n, and bj – real constants for j = 1, ··· , m. How do I find the LCCODE (1)? .
    [Show full text]
  • Linear Filtering of Random Processes
    Linear Filtering of Random Processes Lecture 13 Spring 2002 Wide-Sense Stationary A stochastic process X(t) is wss if its mean is constant E[X(t)] = µ and its autocorrelation depends only on τ = t1 − t2 ∗ Rxx(t1,t2)=E[X(t1)X (t2)] ∗ E[X(t + τ)X (t)] = Rxx(τ) ∗ Note that Rxx(−τ)=Rxx(τ)and Rxx(0) = E[|X(t)|2] Lecture 13 1 Example We found that the random telegraph signal has the autocorrelation function −c|τ| Rxx(τ)=e We can use the autocorrelation function to find the second moment of linear combinations such as Y (t)=aX(t)+bX(t − t0). 2 2 Ryy(0) = E[Y (t)] = E[(aX(t)+bX(t − t0)) ] 2 2 2 2 = a E[X (t)] + 2abE[X(t)X(t − t0)] + b E[X (t − t0)] 2 2 = a Rxx(0) + 2abRxx(t0)+b Rxx(0) 2 2 =(a + b )Rxx(0) + 2abRxx(t0) −ct =(a2 + b2)Rxx(0) + 2abe 0 Lecture 13 2 Example (continued) We can also compute the autocorrelation Ryy(τ)forτ =0. ∗ Ryy(τ)=E[Y (t + τ)Y (t)] = E[(aX(t + τ)+bX(t + τ − t0))(aX(t)+bX(t − t0))] 2 = a E[X(t + τ)X(t)] + abE[X(t + τ)X(t − t0)] 2 + abE[X(t + τ − t0)X(t)] + b E[X(t + τ − t0)X(t − t0)] 2 2 = a Rxx(τ)+abRxx(τ + t0)+abRxx(τ − t0)+b Rxx(τ) 2 2 =(a + b )Rxx(τ)+abRxx(τ + t0)+abRxx(τ − t0) Lecture 13 3 Linear Filtering of Random Processes The above example combines weighted values of X(t)andX(t − t0) to form Y (t).
    [Show full text]
  • Control Theory
    Control theory S. Simrock DESY, Hamburg, Germany Abstract In engineering and mathematics, control theory deals with the behaviour of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain ref- erence over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system. Rapid advances in digital system technology have radically altered the control design options. It has become routinely practicable to design very complicated digital controllers and to carry out the extensive calculations required for their design. These advances in im- plementation and design capability can be obtained at low cost because of the widespread availability of inexpensive and powerful digital processing plat- forms and high-speed analog IO devices. 1 Introduction The emphasis of this tutorial on control theory is on the design of digital controls to achieve good dy- namic response and small errors while using signals that are sampled in time and quantized in amplitude. Both transform (classical control) and state-space (modern control) methods are described and applied to illustrative examples. The transform methods emphasized are the root-locus method of Evans and fre- quency response. The state-space methods developed are the technique of pole assignment augmented by an estimator (observer) and optimal quadratic-loss control. The optimal control problems use the steady-state constant gain solution. Other topics covered are system identification and non-linear control. System identification is a general term to describe mathematical tools and algorithms that build dynamical models from measured data.
    [Show full text]
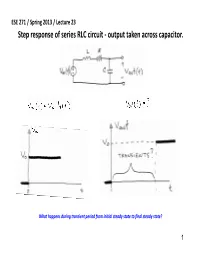
  • Step Response of Series RLC Circuit ‐ Output Taken Across Capacitor
    ESE 271 / Spring 2013 / Lecture 23 Step response of series RLC circuit ‐ output taken across capacitor. What happens during transient period from initial steady state to final steady state? 1 ESE 271 / Spring 2013 / Lecture 23 Transfer function of series RLC ‐ output taken across capacitor. Poles: Case 1: ‐‐two differen t real poles Case 2: ‐ two identical real poles ‐ complex conjugate poles Case 3: 2 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Step response of series RLC ‐ output taken across capacitor. Overdamped case –the circuit demonstrates relatively slow transient response. 3 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Uncorrected Bode Gain Plot Overdamped case –the circuit demonstrates relatively limited bandwidth 4 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Step response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the shortest possible rise time without overshoot. 5 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the widest bandwidth without apparent resonance. Uncorrected Bode Gain Plot 6 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Step response of series RLC ‐ output taken across capacitor. Underdamped case – the circuit oscillates. 7 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Corrected Bode GiGain Plot Underdamped case –the circuit can demonstrate apparent resonant behavior.
    [Show full text]
  • Frequency Response and Bode Plots
    1 Frequency Response and Bode Plots 1.1 Preliminaries The steady-state sinusoidal frequency-response of a circuit is described by the phasor transfer function Hj( ) . A Bode plot is a graph of the magnitude (in dB) or phase of the transfer function versus frequency. Of course we can easily program the transfer function into a computer to make such plots, and for very complicated transfer functions this may be our only recourse. But in many cases the key features of the plot can be quickly sketched by hand using some simple rules that identify the impact of the poles and zeroes in shaping the frequency response. The advantage of this approach is the insight it provides on how the circuit elements influence the frequency response. This is especially important in the design of frequency-selective circuits. We will first consider how to generate Bode plots for simple poles, and then discuss how to handle the general second-order response. Before doing this, however, it may be helpful to review some properties of transfer functions, the decibel scale, and properties of the log function. Poles, Zeroes, and Stability The s-domain transfer function is always a rational polynomial function of the form Ns() smm as12 a s m asa Hs() K K mm12 10 (1.1) nn12 n Ds() s bsnn12 b s bsb 10 As we have seen already, the polynomials in the numerator and denominator are factored to find the poles and zeroes; these are the values of s that make the numerator or denominator zero. If we write the zeroes as zz123,, zetc., and similarly write the poles as pp123,, p , then Hs( ) can be written in factored form as ()()()s zsz sz Hs() K 12 m (1.2) ()()()s psp12 sp n 1 © Bob York 2009 2 Frequency Response and Bode Plots The pole and zero locations can be real or complex.
    [Show full text]
  • T/HIS 15.0 User Manual
    For help and support from Oasys Ltd please contact: UK The Arup Campus Blythe Valley Park Solihull B90 8AE United Kingdom Tel: +44 121 213 3399 Email: [email protected] China Arup 39/F-41/F Huaihai Plaza 1045 Huaihai Road (M) Xuhui District Shanghai 200031 China Tel: +86 21 3118 8875 Email: [email protected] India Arup Ananth Info Park Hi-Tec City Madhapur Phase-II Hyderabad 500 081, Telangana India Tel: +91 40 44369797 / 98 Email: [email protected] Web:www.arup.com/dyna or contact your local Oasys Ltd distributor. LS-DYNA, LS-OPT and LS-PrePost are registered trademarks of Livermore Software Technology Corporation User manual Version 15.0, May 2018 T/HIS 0 Preamble 0.1 Text conventions used in this manual 0.1 1 Introduction 1.1 1.1 Program Limits 1.1 1.2 Running T/HIS 1.2 1.3 Command Line Options 1.4 2 Using Screen Menus 2.1 2.1 Basic screen menu layout 2.1 2.2 Mouse and keyboard usage for screen-menu interface 2.2 2.3 Dialogue input in the screen menu interface 2.4 2.4 Window management in the screen interface 2.4 2.5 Dynamic Viewing (Using the mouse to change views). 2.5 2.6 "Tool Bar" Options 2.6 3 Graphs and Pages 3.1 3.1 Creating Graphs 3.1 3.2 Page Size 3.2 3.3 Page Layouts 3.2 3.3.1 Automatic Page Layout 3.2 3.4 Pages 3.6 3.5 Active Graphs 3.6 4 Global Commands and Pages 4.1 4.1 Page Number 4.1 4.2 PLOT (PL) 4.1 4.3 POINT (PT) 4.2 4.4 CLEAR (CL) 4.2 4.5 ZOOM (ZM) 4.2 4.6 AUTOSCALE (AU) 4.2 4.7 CENTRE (CE) 4.2 4.8 MANUAL 4.2 4.9 STOP 4.2 4.10 TIDY 4.2 4.11 Additional Commands 4.3 5 Main Menu 5.1 5.0 Selecting Curves
    [Show full text]
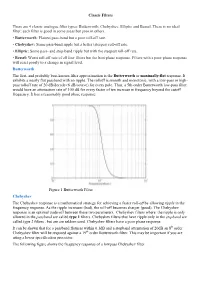
  • Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
    Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used.
    [Show full text]
  • Linear Time Invariant Systems
    UNIT III LINEAR TIME INVARIANT CONTINUOUS TIME SYSTEMS CT systems – Linear Time invariant Systems – Basic properties of continuous time systems – Linearity, Causality, Time invariance, Stability – Frequency response of LTI systems – Analysis and characterization of LTI systems using Laplace transform – Computation of impulse response and transfer function using Laplace transform – Differential equation – Impulse response – Convolution integral and Frequency response. System A system may be defined as a set of elements or functional blocks which are connected together and produces an output in response to an input signal. The response or output of the system depends upon transfer function of the system. Mathematically, the functional relationship between input and output may be written as y(t)=f[x(t)] Types of system Like signals, systems may also be of two types as under: 1. Continuous-time system 2. Discrete time system Continuous time System Continuous time system may be defined as those systems in which the associated signals are also continuous. This means that input and output of continuous – time system are both continuous time signals. For example: Audio, video amplifiers, power supplies etc., are continuous time systems. Discrete time systems Discrete time system may be defined as a system in which the associated signals are also discrete time signals. This means that in a discrete time system, the input and output are both discrete time signals. For example, microprocessors, semiconductor memories, shift registers etc., are discrete time signals. LTI system:- Systems are broadly classified as continuous time systems and discrete time systems. Continuous time systems deal with continuous time signals and discrete time systems deal with discrete time system.
    [Show full text]
  • Chapter 3 FILTERS
    Chapter 3 FILTERS Most images are a®ected to some extent by noise, that is unexplained variation in data: disturbances in image intensity which are either uninterpretable or not of interest. Image analysis is often simpli¯ed if this noise can be ¯ltered out. In an analogous way ¯lters are used in chemistry to free liquids from suspended impurities by passing them through a layer of sand or charcoal. Engineers working in signal processing have extended the meaning of the term ¯lter to include operations which accentuate features of interest in data. Employing this broader de¯nition, image ¯lters may be used to emphasise edges | that is, boundaries between objects or parts of objects in images. Filters provide an aid to visual interpretation of images, and can also be used as a precursor to further digital processing, such as segmentation (chapter 4). Most of the methods considered in chapter 2 operated on each pixel separately. Filters change a pixel's value taking into account the values of neighbouring pixels too. They may either be applied directly to recorded images, such as those in chapter 1, or after transformation of pixel values as discussed in chapter 2. To take a simple example, Figs 3.1(b){(d) show the results of applying three ¯lters to the cashmere ¯bres image, which has been redisplayed in Fig 3.1(a). ² Fig 3.1(b) is a display of the output from a 5 £ 5 moving average ¯lter. Each pixel has been replaced by the average of pixel values in a 5 £ 5 square, or window centred on that pixel.
    [Show full text]
  • A Multidimensional Filtering Framework with Applications to Local Structure Analysis and Image Enhancement
    Linkoping¨ Studies in Science and Technology Dissertation No. 1171 A Multidimensional Filtering Framework with Applications to Local Structure Analysis and Image Enhancement Bjorn¨ Svensson Department of Biomedical Engineering Linkopings¨ universitet SE-581 85 Linkoping,¨ Sweden http://www.imt.liu.se Linkoping,¨ April 2008 A Multidimensional Filtering Framework with Applications to Local Structure Analysis and Image Enhancement c 2008 Bjorn¨ Svensson Department of Biomedical Engineering Linkopings¨ universitet SE-581 85 Linkoping,¨ Sweden ISBN 978-91-7393-943-0 ISSN 0345-7524 Printed in Linkoping,¨ Sweden by LiU-Tryck 2008 Abstract Filtering is a fundamental operation in image science in general and in medical image science in particular. The most central applications are image enhancement, registration, segmentation and feature extraction. Even though these applications involve non-linear processing a majority of the methodologies available rely on initial estimates using linear filters. Linear filtering is a well established corner- stone of signal processing, which is reflected by the overwhelming amount of literature on finite impulse response filters and their design. Standard techniques for multidimensional filtering are computationally intense. This leads to either a long computation time or a performance loss caused by approximations made in order to increase the computational efficiency. This dis- sertation presents a framework for realization of efficient multidimensional filters. A weighted least squares design criterion ensures preservation of the performance and the two techniques called filter networks and sub-filter sequences significantly reduce the computational demand. A filter network is a realization of a set of filters, which are decomposed into a structure of sparse sub-filters each with a low number of coefficients.
    [Show full text]
  • Comparison of a Low-Frequency Butterworth Filter with a Symmetric SE-Filter
    Comparison of a low-frequency Butterworth filter with a symmetric SE-filter K S Medvedeva1 1Saratov State University, Astrakhanskaya Street 83, Saratov, Russia, 410012 Abstract. The article compares two filters: a Butterworth filter and an asymmetric SE- filter.The experimental studydetermines their advantages and disadvantages.Also,experiments based on the peak signal-to-noise ratio(PSNR) metricshowvisual evaluation. The results of experimentsshow that a symmetric filter better restores images usinga small set of continuous function parametersthatare distorted by a low-frequency Gaussian filter. 1. Introduction Due to the imperfection of forming and recording systems, images recorded by systemsare distorted (fuzzy) copiesof the original images. The main causes of distortions that resultindegradation of clarity includethe limited resolution of the forming system, refocusing, the presence of a distorting medium (for example, the atmosphere), and movement of the camera on the object being registered. Eliminating or reducing distortion for clarity is the task of image recovery. Automatic control systems, measuring equipment, signal processing systems, and various filters with different characteristics are used to filter signalsin telecommunications. Depending on the frequency band associated with the bandwidth and the suppression band, there are odd, band, high- frequency, and low-frequency filters. Also, all-pass filters have a constant amplitude-frequency response in the required frequency range, and their phase-frequency response is a given frequency function [1]. The simplest way to restoreimage clarity is to process the observed image in the spatial frequency domain with an inverse filter [2].The drawbacks of this filter are the occurrence of edge effects, which take the form of an oscillating hindrance of high power that completely masksthe reconstructed image.
    [Show full text]