DOCSLIB.ORG

ENCM 369 Winter 2014 Lab 12 for the Week of April 7

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ENCM 369 Winter 2014 Lab 12 for the Week of April 7 page 1 of 7 ENCM 369 Winter 2014 Lab 12 for the Week of April 7 Steve Norman Department of Electrical & Computer Engineering University of Calgary April 2014 Lab instructions and other documents for ENCM 369 can be found at http://www.enel.ucalgary.ca/People/Norman/encm369winter2014/ 1 This Lab is important, but will not be marked Solutions will be posted sometime during the week of April 7. Please make a serious effort to solve the Exercises yourself before checking so- lutions! You can expect a significant portion of the marks on the final exam to be related to integer multiplication and division, and to floating-point number representation and arithmetic. 2 Exercise A: Practice with mult, multu, div, divu 2.1 Read This First mult and multu were the original integer MIPS multiplication instructions, and are the ones explained in lectures and your textbook. Please use these instructions in this exercise, not any other instructions. There is one more real MIPS instruction for integer multiplication: mul. The mul instruction has two GPRs as sources, and writes bits 31{0 of the product directly to a destination GPR. This is useful for compilers|a compiler can avoid using a mflo instruction when only the low 32 bits of an integer product are needed. MARS assembly language also allows a lot of pseudoinstructions for integer division and multiplication, for example, allowing constants instead of GPRs as sources. Please avoid these pseudoinstructions. To keep things as simple as possible, the ENCM 360 final exam in Winter 2014 will test you on the real instructions mult, multu, div, and divu, not any other real instructions or pseudoinstructions for integer multiplication or division. Of course, that implies that you also need to know how to use mflo or mfhi to copy a result out of Lo or Hi into a GPR. 2.2 What to Do Copy the files in encm369w14lab12/exA Read the two files. You should see that ex12A.asm is a nearly complete translation of ex12A.c|all the tedious work of translating main has been done. However, code must be added to ex12A.asm for the procedures func1 and func2. ENCM 369 Winter 2014 Lab 12 page 2 of 7 Make a copy of ex12A.asm, and add appropriate instructions to func1 and func2 to properly translate the C versions. If you do this correctly, the output of the MARS program should show you the same numbers as the output of the C program. In doing the translation, • do not modify main in any way; • handle multiplication as a typical C compiler would|the result of multiplying two 32-bit integers should be taken as the low 32 bits of the 64-bit product; • do not worry about the possibility of division by zero|in this exercise, you do not need to write code for special behaviour in the case of a zero divisor. 3 Exercise B: IEEE 754 floating-point formats 3.1 Read This First You should be able to do all parts of this exercise with just pencil and paper|the numbers have been set up to make the arithmetic easy to do. 3.2 What to Do Answer the following questions. In each case, take time to write down the steps you take to work toward an answer. 1. If the 32-bit IEEE 754 format is being used, what number does the bit pattern 0xc0a8_0000 represent? 2. If the 32-bit IEEE 754 format is being used, what number does the bit pattern 0x3f20_0000 represent? 3. If the 64-bit IEEE 754 format is being used, what number does the bit pattern 0x4015_0000_0000_0000 represent? 4. If the 64-bit IEEE 754 format is being used, what number does the bit pattern 0xfff0_0000_0000_0000 represent? 5. What is the 32-bit IEEE 754 representation of −3:25? Express your final answer using hexadecimal notation. 6. What is the 64-bit IEEE 754 representation of −3:25? Express your final answer using hexadecimal notation. 4 Exercise C: The minifloat type 4.1 Read This First To understand how floating-point number representation and arithmetic work, it's useful to consider some pencil-and-paper examples. However, doing pencil-and- paper work with 32-bit patterns (or worse, 64-bit patterns) is tedious, so in this exercise we'll do it with an 8-bit floating-point type called the minifloat type. The minifloat type is intended to mimic the IEEE 754 32-bit and 64-bit floating-point types. With only 8 bits, the precision and range of magnitudes for minifloat will obviously be severely limited. The layout of a minifloat is as follows: ENCM 369 Winter 2014 Lab 12 page 3 of 7 bit 7: sign bits 3-0: bit fraction bits 6-4: biased exponent Before continuing to describe the minifloat type, I would like to introduce a bit of notation. I will use the ** operator (borrowed from the Fortran and Python pro- gramming languages) for exponentiation; this is handy when writing mathematics in Web pages and program comments. (So, for example, 2**4 means 24.) Here is the specification for the minifloat type: • The sign bit of a minifloat is 0 for positive numbers and 1 for negative numbers. • The exponent field of a minifloat is used as follows: { Bit patterns 001, 010, 011, 100, 101 and 110 are used for exponents of normal, nonzero numbers. There is a bias of three in the exponent. { The bit pattern 000 is the exponent field in for representations of zero. (IEEE 754 types use all-0 exponents for zero values and also for very- small-magnitude nonzero values called denormalized numbers; we won't bother with denormalized numbers in the minifloat type.) { The bit pattern 111 is not used at all. (IEEE 754 types use all-1 expo- nents to indicate special values of Infinity and NaN|\not a number". We won't bother with Infinity and NaN in the minifloat type.) • In a nonzero minifloat, the fraction bits are used to represent the fractional part of the significand. In representations of zero, the fraction bits must all be 0. Now that the uses of the individual fields have been described, it's possible to determine what real number (if any) is represented by an 8-bit pattern. • First of all, both 00000000 and 10000000 represent zero; note that in an IEEE 754 system, there are also two representations of zero. • Next, there are some bit patterns that don't represent any real number at all. Examples are: 10001010, which has a special exponent of 000 but does not have 0000 in its fraction field; and 01110000, which has the meaningless exponent of 111. • Finally, there are normal, nonzero numbers, such as 01101011. To see what number this is, first split it into fields: the sign bit is 0, the exponent field is 110, and the fraction field is 1011. In base two, then, the number represented is 1.1011 * two ** three Note that the significand is obtained by putting a 1 and a binary point in front of the four-bit fraction field and that the exponent of three is obtained by subtracting the bias of three from the value of six (110). In base ten, the number is (1 + 1=2 + 1=8 + 1=16) × 23 = 1:6875 × 8 = 13:5. ENCM 369 Winter 2014 Lab 12 page 4 of 7 Let's consider the problem of determining a minifloat representation of a number given in base 10, say 0.390625. To start with we need to write our number in the form sign * significand * 2 ** exponent where the significand is greater than or equal to 1 and less than 2. This gives us 0.390625 = 1 * 1.5625 * 2 ** (-2) The sign bit should be 0, obviously. The biased exponent should be −2 + 3, or 001 in base two. What is the fractional part of the significand? Here I will cheat a little and just state that 0.5625 is in fact exactly 1=2 + 1=16, so the correct bit pattern is 1001. Putting all the bit fields together, the minifloat representation is 00011001. The fractional part of the significand in a minifloat is bit3 / 2 + bit2 / 4 + bit1 / 8 + bit0 / 16 From this it should be clear that the fractional part of the significand is always an integer multiple of 1/16. Determining the significand bits in the previous example was relatively easy because 0.5625 just happened to be an integer multiple of 1/16. Most base ten fractions are not integer multiples of 1/16, so usually when converting from base ten to minifloat, the fraction will have to be rounded to an integer multiple of 1/16. The following table is useful for doing such rounding: value base two base ten value base two base ten 0/16 0.0000 0.0000 8/16 0.1000 0.5000 1/16 0.0001 0.0625 9/16 0.1001 0.5625 2/16 0.0010 0.1250 10/16 0.1010 0.6250 3/16 0.0011 0.1875 11/16 0.1011 0.6875 4/16 0.0100 0.2500 12/16 0.1100 0.7500 5/16 0.0101 0.3125 13/16 0.1101 0.8125 6/16 0.0110 0.3750 14/16 0.1110 0.8750 7/16 0.0111 0.4375 15/16 0.1111 0.9375 Let's find a minifloat representation for −3:6, which is −1 × 1:8 × 21. The sign bit is 1 and the exponent field is 100.
Load more

Recommended publications
  • Bit Nove Signal Interface Processor
    www.audison.eu bit Nove Signal Interface Processor POWER SUPPLY CONNECTION Voltage 10.8 ÷ 15 VDC From / To Personal Computer 1 x Micro USB Operating power supply voltage 7.5 ÷ 14.4 VDC To Audison DRC AB / DRC MP 1 x AC Link Idling current 0.53 A Optical 2 sel Optical In 2 wire control +12 V enable Switched off without DRC 1 mA Mem D sel Memory D wire control GND enable Switched off with DRC 4.5 mA CROSSOVER Remote IN voltage 4 ÷ 15 VDC (1mA) Filter type Full / Hi pass / Low Pass / Band Pass Remote OUT voltage 10 ÷ 15 VDC (130 mA) Linkwitz @ 12/24 dB - Butterworth @ Filter mode and slope ART (Automatic Remote Turn ON) 2 ÷ 7 VDC 6/12/18/24 dB Crossover Frequency 68 steps @ 20 ÷ 20k Hz SIGNAL STAGE Phase control 0° / 180° Distortion - THD @ 1 kHz, 1 VRMS Output 0.005% EQUALIZER (20 ÷ 20K Hz) Bandwidth @ -3 dB 10 Hz ÷ 22 kHz S/N ratio @ A weighted Analog Input Equalizer Automatic De-Equalization N.9 Parametrics Equalizers: ±12 dB;10 pole; Master Input 102 dBA Output Equalizer 20 ÷ 20k Hz AUX Input 101.5 dBA OPTICAL IN1 / IN2 Inputs 110 dBA TIME ALIGNMENT Channel Separation @ 1 kHz 85 dBA Distance 0 ÷ 510 cm / 0 ÷ 200.8 inches Input sensitivity Pre Master 1.2 ÷ 8 VRMS Delay 0 ÷ 15 ms Input sensitivity Speaker Master 3 ÷ 20 VRMS Step 0,08 ms; 2,8 cm / 1.1 inch Input sensitivity AUX Master 0.3 ÷ 5 VRMS Fine SET 0,02 ms; 0,7 cm / 0.27 inch Input impedance Pre In / Speaker In / AUX 15 kΩ / 12 Ω / 15 kΩ GENERAL REQUIREMENTS Max Output Level (RMS) @ 0.1% THD 4 V PC connections USB 1.1 / 2.0 / 3.0 Compatible Microsoft Windows (32/64 bit): Vista, INPUT STAGE Software/PC requirements Windows 7, Windows 8, Windows 10 Low level (Pre) Ch1 ÷ Ch6; AUX L/R Video Resolution with screen resize min.
    [Show full text]
  • Harnessing Numerical Flexibility for Deep Learning on Fpgas.Pdf
    WHITE PAPER FPGA Inline Acceleration Harnessing Numerical Flexibility for Deep Learning on FPGAs Authors Abstract Andrew C . Ling Deep learning has become a key workload in the data center and the edge, leading [email protected] to a race for dominance in this space. FPGAs have shown they can compete by combining deterministic low latency with high throughput and flexibility. In Mohamed S . Abdelfattah particular, FPGAs bit-level programmability can efficiently implement arbitrary [email protected] precisions and numeric data types critical in the fast evolving field of deep learning. Andrew Bitar In this paper, we explore FPGA minifloat implementations (floating-point [email protected] representations with non-standard exponent and mantissa sizes), and show the use of a block-floating-point implementation that shares the exponent across David Han many numbers, reducing the logic required to perform floating-point operations. [email protected] The paper shows this technique can significantly improve FPGA performance with no impact to accuracy, reduce logic utilization by 3X, and memory bandwidth and Roberto Dicecco capacity required by more than 40%.† [email protected] Suchit Subhaschandra Introduction [email protected] Deep neural networks have proven to be a powerful means to solve some of the Chris N Johnson most difficult computer vision and natural language processing problems since [email protected] their successful introduction to the ImageNet competition in 2012 [14]. This has led to an explosion of workloads based on deep neural networks in the data center Dmitry Denisenko and the edge [2]. [email protected] One of the key challenges with deep neural networks is their inherent Josh Fender computational complexity, where many deep nets require billions of operations [email protected] to perform a single inference.
    [Show full text]
  • Midterm-2020-Solution.Pdf
    HONOR CODE Questions Sheet. A Lets C. [6 Points] 1. What type of address (heap,stack,static,code) does each value evaluate to Book1, Book1->name, Book1->author, &Book2? [4] 2. Will all of the print statements execute as expected? If NO, write print statement which will not execute as expected?[2] B. Mystery [8 Points] 3. When the above code executes, which line is modified? How many times? [2] 4. What is the value of register a6 at the end ? [2] 5. What is the value of register a4 at the end ? [2] 6. In one sentence what is this program calculating ? [2] C. C-to-RISC V Tree Search; Fill in the blanks below [12 points] D. RISCV - The MOD operation [8 points] 19. The data segment starts at address 0x10000000. What are the memory locations modified by this program and what are their values ? E Floating Point [8 points.] 20. What is the smallest nonzero positive value that can be represented? Write your answer as a numerical expression in the answer packet? [2] 21. Consider some positive normalized floating point number where p is represented as: What is the distance (i.e. the difference) between p and the next-largest number after p that can be represented? [2] 22. Now instead let p be a positive denormalized number described asp = 2y x 0.significand. What is the distance between p and the next largest number after p that can be represented? [2] 23. Sort the following minifloat numbers. [2] F. Numbers. [5] 24. What is the smallest number that this system can represent 6 digits (assume unsigned) ? [1] 25.
    [Show full text]
  • Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
    Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic.
    [Show full text]
  • Metaclasses: Generative C++
    Metaclasses: Generative C++ Document Number: P0707 R3 Date: 2018-02-11 Reply-to: Herb Sutter ([email protected]) Audience: SG7, EWG Contents 1 Overview .............................................................................................................................................................2 2 Language: Metaclasses .......................................................................................................................................7 3 Library: Example metaclasses .......................................................................................................................... 18 4 Applying metaclasses: Qt moc and C++/WinRT .............................................................................................. 35 5 Alternatives for sourcedefinition transform syntax .................................................................................... 41 6 Alternatives for applying the transform .......................................................................................................... 43 7 FAQs ................................................................................................................................................................. 46 8 Revision history ............................................................................................................................................... 51 Major changes in R3: Switched to function-style declaration syntax per SG7 direction in Albuquerque (old: $class M new: constexpr void M(meta::type target,
    [Show full text]
  • Meta-Class Features for Large-Scale Object Categorization on a Budget
    Meta-Class Features for Large-Scale Object Categorization on a Budget Alessandro Bergamo Lorenzo Torresani Dartmouth College Hanover, NH, U.S.A. faleb, [email protected] Abstract cation accuracy over a predefined set of classes, and without consideration of the computational costs of the recognition. In this paper we introduce a novel image descriptor en- We believe that these two assumptions do not meet the abling accurate object categorization even with linear mod- requirements of modern applications of large-scale object els. Akin to the popular attribute descriptors, our feature categorization. For example, test-recognition efficiency is a vector comprises the outputs of a set of classifiers evaluated fundamental requirement to be able to scale object classi- on the image. However, unlike traditional attributes which fication to Web photo repositories, such as Flickr, which represent hand-selected object classes and predefined vi- are growing at rates of several millions new photos per sual properties, our features are learned automatically and day. Furthermore, while a fixed set of object classifiers can correspond to “abstract” categories, which we name meta- be used to annotate pictures with a set of predefined tags, classes. Each meta-class is a super-category obtained by the interactive nature of searching and browsing large im- grouping a set of object classes such that, collectively, they age collections calls for the ability to allow users to define are easy to distinguish from other sets of categories. By us- their own personal query categories to be recognized and ing “learnability” of the meta-classes as criterion for fea- retrieved from the database, ideally in real-time.
    [Show full text]
  • IEEE Standard 754 for Binary Floating-Point Arithmetic
    Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite
    [Show full text]
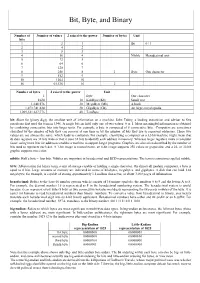
  • Bit, Byte, and Binary
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]
  • SPARC Assembly Language Reference Manual
    SPARC Assembly Language Reference Manual 2550 Garcia Avenue Mountain View, CA 94043 U.S.A. A Sun Microsystems, Inc. Business 1995 Sun Microsystems, Inc. 2550 Garcia Avenue, Mountain View, California 94043-1100 U.S.A. All rights reserved. This product or document is protected by copyright and distributed under licenses restricting its use, copying, distribution and decompilation. No part of this product or document may be reproduced in any form by any means without prior written authorization of Sun and its licensors, if any. Portions of this product may be derived from the UNIX® system, licensed from UNIX Systems Laboratories, Inc., a wholly owned subsidiary of Novell, Inc., and from the Berkeley 4.3 BSD system, licensed from the University of California. Third-party software, including font technology in this product, is protected by copyright and licensed from Sun’s Suppliers. RESTRICTED RIGHTS LEGEND: Use, duplication, or disclosure by the government is subject to restrictions as set forth in subparagraph (c)(1)(ii) of the Rights in Technical Data and Computer Software clause at DFARS 252.227-7013 and FAR 52.227-19. The product described in this manual may be protected by one or more U.S. patents, foreign patents, or pending applications. TRADEMARKS Sun, Sun Microsystems, the Sun logo, SunSoft, the SunSoft logo, Solaris, SunOS, OpenWindows, DeskSet, ONC, ONC+, and NFS are trademarks or registered trademarks of Sun Microsystems, Inc. in the United States and other countries. UNIX is a registered trademark in the United States and other countries, exclusively licensed through X/Open Company, Ltd. OPEN LOOK is a registered trademark of Novell, Inc.
    [Show full text]
  • X86-64 Machine-Level Programming∗
    x86-64 Machine-Level Programming∗ Randal E. Bryant David R. O'Hallaron September 9, 2005 Intel’s IA32 instruction set architecture (ISA), colloquially known as “x86”, is the dominant instruction format for the world’s computers. IA32 is the platform of choice for most Windows and Linux machines. The ISA we use today was defined in 1985 with the introduction of the i386 microprocessor, extending the 16-bit instruction set defined by the original 8086 to 32 bits. Even though subsequent processor generations have introduced new instruction types and formats, many compilers, including GCC, have avoided using these features in the interest of maintaining backward compatibility. A shift is underway to a 64-bit version of the Intel instruction set. Originally developed by Advanced Micro Devices (AMD) and named x86-64, it is now supported by high end processors from AMD (who now call it AMD64) and by Intel, who refer to it as EM64T. Most people still refer to it as “x86-64,” and we follow this convention. Newer versions of Linux and GCC support this extension. In making this switch, the developers of GCC saw an opportunity to also make use of some of the instruction-set features that had been added in more recent generations of IA32 processors. This combination of new hardware and revised compiler makes x86-64 code substantially different in form and in performance than IA32 code. In creating the 64-bit extension, the AMD engineers also adopted some of the features found in reduced-instruction set computers (RISC) [7] that made them the favored targets for optimizing compilers.
    [Show full text]
  • Floating Point Arithmetic
    Systems Architecture Lecture 14: Floating Point Arithmetic Jeremy R. Johnson Anatole D. Ruslanov William M. Mongan Some or all figures from Computer Organization and Design: The Hardware/Software Approach, Third Edition, by David Patterson and John Hennessy, are copyrighted material (COPYRIGHT 2004 MORGAN KAUFMANN PUBLISHERS, INC. ALL RIGHTS RESERVED). Lec 14 Systems Architecture 1 Introduction • Objective: To provide hardware support for floating point arithmetic. To understand how to represent floating point numbers in the computer and how to perform arithmetic with them. Also to learn how to use floating point arithmetic in MIPS. • Approximate arithmetic – Finite Range – Limited Precision • Topics – IEEE format for single and double precision floating point numbers – Floating point addition and multiplication – Support for floating point computation in MIPS Lec 14 Systems Architecture 2 Distribution of Floating Point Numbers e = -1 e = 0 e = 1 • 3 bit mantissa 1.00 X 2^(-1) = 1/2 1.00 X 2^0 = 1 1.00 X 2^1 = 2 1.01 X 2^(-1) = 5/8 1.01 X 2^0 = 5/4 1.01 X 2^1 = 5/2 • exponent {-1,0,1} 1.10 X 2^(-1) = 3/4 1.10 X 2^0 = 3/2 1.10 X 2^1= 3 1.11 X 2^(-1) = 7/8 1.11 X 2^0 = 7/4 1.11 X 2^1 = 7/2 0 1 2 3 Lec 14 Systems Architecture 3 Floating Point • An IEEE floating point representation consists of – A Sign Bit (no surprise) – An Exponent (“times 2 to the what?”) – Mantissa (“Significand”), which is assumed to be 1.xxxxx (thus, one bit of the mantissa is implied as 1) – This is called a normalized representation • So a mantissa = 0 really is interpreted to be 1.0, and a mantissa of all 1111 is interpreted to be 1.1111 • Special cases are used to represent denormalized mantissas (true mantissa = 0), NaN, etc., as will be discussed.
    [Show full text]
  • FPGA Based Quadruple Precision Floating Point Arithmetic for Scientific Computations
    International Journal of Advanced Computer Research (ISSN (print): 2249-7277 ISSN (online): 2277-7970) Volume-2 Number-3 Issue-5 September-2012 FPGA Based Quadruple Precision Floating Point Arithmetic for Scientific Computations 1Mamidi Nagaraju, 2Geedimatla Shekar 1Department of ECE, VLSI Lab, National Institute of Technology (NIT), Calicut, Kerala, India 2Asst.Professor, Department of ECE, Amrita Vishwa Vidyapeetham University Amritapuri, Kerala, India Abstract amounts, and fractions are essential to many computations. Floating-point arithmetic lies at the In this project we explore the capability and heart of computer graphics cards, physics engines, flexibility of FPGA solutions in a sense to simulations and many models of the natural world. accelerate scientific computing applications which Floating-point computations suffer from errors due to require very high precision arithmetic, based on rounding and quantization. Fast computers let IEEE 754 standard 128-bit floating-point number programmers write numerically intensive programs, representations. Field Programmable Gate Arrays but computed results can be far from the true results (FPGA) is increasingly being used to design high due to the accumulation of errors in arithmetic end computationally intense microprocessors operations. Implementing floating-point arithmetic in capable of handling floating point mathematical hardware can solve two separate problems. First, it operations. Quadruple Precision Floating-Point greatly speeds up floating-point arithmetic and Arithmetic is important in computational fluid calculations. Implementing a floating-point dynamics and physical modelling, which require instruction will require at a generous estimate at least accurate numerical computations. However, twenty integer instructions, many of them conditional modern computers perform binary arithmetic, operations, and even if the instructions are executed which has flaws in representing and rounding the on an architecture which goes to great lengths to numbers.
    [Show full text]