DOCSLIB.ORG

Chapter 2. Fourier Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 2. Fourier Analysis CHAPTER TREFETHEN Chapter Fourier Analysis The Fourier transform The semidiscrete Fourier transform Interp olation and sinc functions The discrete Fourier transform Vectors and multiple space dimensions Notes and references Untwisting all the chains that tie the hidden soul of harmony JOHN MILTON LAllegro CHAPTER TREFETHEN The last chapter dealt with time dep endence and this one is motivated by space dep endence Later chapters will combine the two Fourier analysis touches almost every asp ect of partial dierential equa tions and their numerical solution Sometimes Fourier ideas enter into the analysis of a numerical algorithm derived from other principlesesp ecially in the stability analysis of nitedierence formulas Sometimes they underlie the design of the algorithm itselfsp ectral metho ds And sometimes the situ ation is a mixture of b oth as with iterativeandmultigrid metho ds for elliptic equations For one reason or another Fourier analysis will app ear in all of the remaining chapters of this b o ok The impact of Fourier analysis is also felt in many elds b esides dier ential equations and their numerical solution such as quantum mechanics crystallography signal pro cessing statistics and information theory There are four varieties of Fourier transform dep ending on whether the spatial domain is unb ounded or bounded continuous or discrete Name Space variable Transform variable Fourier transform unb ounded continuous continuous unb ounded Fourier series bounded continuous discrete unb ounded semidiscrete Fourier transform unb ounded discrete continuous b ounded or z transform discrete Fourier transform b ounded discrete discrete bounded DFT The second and third varieties are mathematically equivalent This chapter will describ e the essentials of these op erations emphasizing the parallels be tween them In discrete metho ds for partial dierential equations one lo oks for a representation that will converge to a solution of the continuous problem as the mesh is rened Our denitions are chosen so that the same kind of convergence holds also for the transforms Rigorous Fourier analysis is a highly technical and highly develop ed area of mathematics which dep ends heavily on the theory of Leb esgue measure and integration We shall make use of L and spaces but for the most part this chapter avoids the technicalities In particular a number of statements made in this chapter hold not at every point of a domain but almost everywhere everywhere but onaset of measure zero THE FOURIER TRANSFORM TREFETHEN The Fourier transform If ux is a Leb esguemeasurable function of x R the L norm of u is the nonnegative or innite real number Z h i kuk juxj dx The symbol L Ltwo denotes the set of all functions for whichthisintegral is nite L fu kuk g and L are the sets of functions having nite L andL norms Similarly L dened by Z juxjdx kuk sup juxj kuk x Note that since the L norm is the norm used in most applications b ecause of its many desirable prop erties we have reserved the symbol kk without a subscript for it The convolution of two functions u v is the function u v dened by Z Z u v x u v x ux y v y dy uy v x y dy assuming these integrals exist One way to think of u v is as a weighted moving average of values uxwithweights dened by v x or vice versa u L the Fourier transform of u is the function u dened For any by Z i x u F u e uxdx R The quantity is known as the wavenumber the spatial analog of frequency this integral converges in the usual sense for all For many functions u L R but there are situations where this is not true and in these cases one must interpret the integral as a limit in a certain L norm sense of integrals R M as M The reader interested in such details should consult the M various b o oks listed in the references If u L then u exists for every and is continuous with resp ect to According to the RiemannLeb esgue Lemma it also satises ju jas THE FOURIER TRANSFORM TREFETHEN x Figure Space and wavenumb er domains for the Fourier trans form compare Figures and The following theorem summarizes some of the fundamental prop erties of Fourier transforms THE FOURIER TRANSFORM Theorem If u L then the Fourier transform Z i x u F u e uxdx R b elongs to L also and u can b e recovered from u bythe inverse Fourier transform Z i x ux F u x e u d x R The L norms of u and u are related by Parsevals equality p ku k kuk d If u L and v L or vice versa then u v L and u v satises d u v u v These four equations are of such fundamental imp ortance that they are worth commenting on individually although it is assumed the reader has al ready been exp osed to Fourier analysis As mentioned in the intro duction to this chapter some of these prop ertiesnamely equations and hold merely for almost every value of x or In fact even if f z is a continuous function in L its Fourier transform may fail to converge at certain p oints x To ensure pointwise convergence one needs additional assumptions such as that f is of b ounded variation dened b elow b efore Theorem and b elongs to L These assumptions also ensure that at any point x where f has a jump discontinuity its Fourier transform converges to the average value f x f x THE FOURIER TRANSFORM TREFETHEN First of all indicates that u is a measure of the correlation of i x ux with the function e The idea behind Fourier analysis is to interpret i x uxas a sup erp osition of mono chromatic waves e with various wave num b ers andu represents the complex amplitude more precisely amplitude density with resp ect to of the comp onentofu at wave number Conversely expresses the synthesis of u x as a sup erp osition of its i x comp onents e each multiplied by the appropriate factor u The factor is a nuisance that could have been put in various places in our formulas but is hard to eliminate entirely Equation Parsevals equality is a statement of energy conserva tion the L energy of any signal ux is equal to the sum of the energies of p By energy we mean its comp onent vibrations except for the factor the square of the L norm Finally the convolution equation is p erhaps the most subtle of d the four The left side u v represents the strength of the wave number comp onent that results when u is convolved with v in other words the degree to which u and v beat in and out of phase with each other at wave number when multiplied together in reverse order with a varying oset Such b eating is caused b y a quadratic interaction of the wave number comp onent in u with the same comp onentofv hence the righthand side u v All of the assertions of Theorem can be veried in the following ex ample which the reader should study carefully EXAMPLE Bsplines Supp ose u is the function for x ux otherwise p Figure Then by wehave kuk and gives Z i x sin e i x e dx u i This functionu is called a sinc function more on these in x From and the indisp ensable identity Z sin s ds s p which can b e derived by complex contour integration we calculate kuk which conrms From the denition it is readily veried that in this example jxj for x u ux otherwise worth memorizing THE FOURIER TRANSFORM TREFETHEN u u x d u u u u x d u u u u u u x Figure The rst three Bsplines of Example and their Fourier trans forms and x for x u u ux jxj x for jxj otherwise and by and the corresp onding Fourier transforms must b e sin sin d d u u u u u See Figure In general a convolution u of p copies of u has the Fourier transform p p sin ud Ffu u ug p Note that whenever u or any other function is convolved with the function u of p it b ecomes smo other since the convolution amounts to a lo cal moving average In particular u itself is piecewise continuous u u is continuous and has a piecewise continuous rst derivative u u u has a continuous derivative and a piecewise continuous second derivative and so on In general u is a piecewise p olynomial of degree p with a p con tinuous p nd derivative and a piecewise continuous p st derivative and is known as a Bspline See for example C de Bo or A Practical Guide to Splines Springer Thus convolution with u makes a function smo other while the eect on the Fourier transform is to multiply it bysin and therebymake it decay more rapidly This relationship is evident in Figure For applications to numerical metho ds for partial dierential equations there are two prop erties of the Fourier transform that are most imp ortant THE FOURIER TRANSFORM TREFETHEN One is equation the Fourier transform converts convolution into mul tiplication The second can be derived by integration by parts Z Z i x i x c u e u xdx i e uxdx i u x x the Fourier transform assuming ux is smo oth and decays at That is converts dierentiation into multiplication by i This result is rigorously valid for any absolutely continuous function u L whose derivative b elongs to L Note that dierentiation makes a function less smo oth so the fact that it makes the Fourier transform decay less rapidly ts the pattern mentioned ab ove for convolution Figure EXAMPLE The function for x ux for x otherwise illustrated in Figure has Fourier transform Z Z i x i x u e dx e dx i sin i i i i e e e e i i whichisi times the Fourier transform of the triangular hat function
Load more

Recommended publications
  • B1. Fourier Analysis of Discrete Time Signals
    B1. Fourier Analysis of Discrete Time Signals Objectives • Introduce discrete time periodic signals • Define the Discrete Fourier Series (DFS) expansion of periodic signals • Define the Discrete Fourier Transform (DFT) of signals with finite length • Determine the Discrete Fourier Transform of a complex exponential 1. Introduction In the previous chapter we defined the concept of a signal both in continuous time (analog) and discrete time (digital). Although the time domain is the most natural, since everything (including our own lives) evolves in time, it is not the only possible representation. In this chapter we introduce the concept of expanding a generic signal in terms of elementary signals, such as complex exponentials and sinusoids. This leads to the frequency domain representation of a signal in terms of its Fourier Transform and the concept of frequency spectrum so that we characterize a signal in terms of its frequency components. First we begin with the introduction of periodic signals, which keep repeating in time. For these signals it is fairly easy to determine an expansion in terms of sinusoids and complex exponentials, since these are just particular cases of periodic signals. This is extended to signals of a finite duration which becomes the Discrete Fourier Transform (DFT), one of the most widely used algorithms in Signal Processing. The concepts introduced in this chapter are at the basis of spectral estimation of signals addressed in the next two chapters. 2. Periodic Signals VIDEO: Periodic Signals (19:45) http://faculty.nps.edu/rcristi/eo3404/b-discrete-fourier-transform/videos/chapter1-seg1_media/chapter1-seg1- 0.wmv http://faculty.nps.edu/rcristi/eo3404/b-discrete-fourier-transform/videos/b1_02_periodicSignals.mp4 In this section we define a class of discrete time signals called Periodic Signals.
    [Show full text]
  • On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle
    On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle Agah D. Garnadi 31 December 2017 Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University Jl. Meranti, Kampus IPB Darmaga, Bogor, 16680 Indonesia Abstract This note is addressed to solving biperiodic boundary value prob- lem of biharmonic equation in the unit rectangle. First, we describe the necessary tools, which is discrete Fourier transform for one di- mensional periodic sequence, and then extended the results to 2- dimensional biperiodic sequence. Next, we use the discrete Fourier transform 2-dimensional biperiodic sequence to solve discretization of the biperiodic boundary value problem of Biharmonic Equation. MSC: 15A09; 35K35; 41A15; 41A29; 94A12. Key words: Biharmonic equation, biperiodic boundary value problem, discrete Fourier transform, Partial differential equations, Interpola- tion. 1 Introduction This note is an extension of a work by Henrici [2] on fast solver for Poisson equation to biperiodic boundary value problem of biharmonic equation. This 1 note is organized as follows, in the first part we address the tools needed to solve the problem, i.e. introducing discrete Fourier transform (DFT) follows Henrici's work [2]. The second part, we apply the tools already described in the first part to solve discretization of biperiodic boundary value problem of biharmonic equation in the unit rectangle. The need to solve discretization of biharmonic equation is motivated by its occurence in some applications such as elasticity and fluid flows [1, 4], and recently in image inpainting [3]. Note that the work of Henrici [2] on fast solver for biperiodic Poisson equation can be seen as solving harmonic inpainting.
    [Show full text]
  • An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms
    An Introduction to Fourier Analysis Fourier Series, Partial Differential Equations and Fourier Transforms Notes prepared for MA3139 Arthur L. Schoenstadt Department of Applied Mathematics Naval Postgraduate School Code MA/Zh Monterey, California 93943 August 18, 2005 c 1992 - Professor Arthur L. Schoenstadt 1 Contents 1 Infinite Sequences, Infinite Series and Improper Integrals 1 1.1Introduction.................................... 1 1.2FunctionsandSequences............................. 2 1.3Limits....................................... 5 1.4TheOrderNotation................................ 8 1.5 Infinite Series . ................................ 11 1.6ConvergenceTests................................ 13 1.7ErrorEstimates.................................. 15 1.8SequencesofFunctions.............................. 18 2 Fourier Series 25 2.1Introduction.................................... 25 2.2DerivationoftheFourierSeriesCoefficients.................. 26 2.3OddandEvenFunctions............................. 35 2.4ConvergencePropertiesofFourierSeries.................... 40 2.5InterpretationoftheFourierCoefficients.................... 48 2.6TheComplexFormoftheFourierSeries.................... 53 2.7FourierSeriesandOrdinaryDifferentialEquations............... 56 2.8FourierSeriesandDigitalDataTransmission.................. 60 3 The One-Dimensional Wave Equation 70 3.1Introduction.................................... 70 3.2TheOne-DimensionalWaveEquation...................... 70 3.3 Boundary Conditions ............................... 76 3.4InitialConditions................................
    [Show full text]
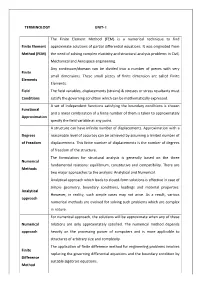
  • TERMINOLOGY UNIT- I Finite Element Method (FEM)
    TERMINOLOGY UNIT- I The Finite Element Method (FEM) is a numerical technique to find Finite Element approximate solutions of partial differential equations. It was originated from Method (FEM) the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. Any continuum/domain can be divided into a number of pieces with very Finite small dimensions. These small pieces of finite dimension are called Finite Elements Elements. Field The field variables, displacements (strains) & stresses or stress resultants must Conditions satisfy the governing condition which can be mathematically expressed. A set of independent functions satisfying the boundary conditions is chosen Functional and a linear combination of a finite number of them is taken to approximately Approximation specify the field variable at any point. A structure can have infinite number of displacements. Approximation with a Degrees reasonable level of accuracy can be achieved by assuming a limited number of of Freedom displacements. This finite number of displacements is the number of degrees of freedom of the structure. The formulation for structural analysis is generally based on the three Numerical fundamental relations: equilibrium, constitutive and compatibility. There are Methods two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. Analytical However, in reality, such simple cases may not arise. As a result, various approach numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these Numerical relations are only approximately satisfied.
    [Show full text]
  • Fourier Analysis
    Chapter 1 Fourier analysis In this chapter we review some basic results from signal analysis and processing. We shall not go into detail and assume the reader has some basic background in signal analysis and processing. As basis for signal analysis, we use the Fourier transform. We start with the continuous Fourier transformation. But in applications on the computer we deal with a discrete Fourier transformation, which introduces the special effect known as aliasing. We use the Fourier transformation for processes such as convolution, correlation and filtering. Some special attention is given to deconvolution, the inverse process of convolution, since it is needed in later chapters of these lecture notes. 1.1 Continuous Fourier Transform. The Fourier transformation is a special case of an integral transformation: the transforma- tion decomposes the signal in weigthed basis functions. In our case these basis functions are the cosine and sine (remember exp(iφ) = cos(φ) + i sin(φ)). The result will be the weight functions of each basis function. When we have a function which is a function of the independent variable t, then we can transform this independent variable to the independent variable frequency f via: +1 A(f) = a(t) exp( 2πift)dt (1.1) −∞ − Z In order to go back to the independent variable t, we define the inverse transform as: +1 a(t) = A(f) exp(2πift)df (1.2) Z−∞ Notice that for the function in the time domain, we use lower-case letters, while for the frequency-domain expression the corresponding uppercase letters are used. A(f) is called the spectrum of a(t).
    [Show full text]
  • Lecture 7: the Complex Fourier Transform and the Discrete Fourier Transform (DFT)
    Lecture 7: The Complex Fourier Transform and the Discrete Fourier Transform (DFT) c Christopher S. Bretherton Winter 2014 7.1 Fourier analysis and filtering Many data analysis problems involve characterizing data sampled on a regular grid of points, e. g. a time series sampled at some rate, a 2D image made of regularly spaced pixels, or a 3D velocity field from a numerical simulation of fluid turbulence on a regular grid. Often, such problems involve characterizing, detecting, separating or ma- nipulating variability on different scales, e. g. finding a weak systematic signal amidst noise in a time series, edge sharpening in an image, or quantifying the energy of motion across the different sizes of turbulent eddies. Fourier analysis using the Discrete Fourier Transform (DFT) is a fun- damental tool for such problems. It transforms the gridded data into a linear combination of oscillations of different wavelengths. This partitions it into scales which can be separately analyzed and manipulated. The computational utility of Fourier methods rests on the Fast Fourier Transform (FFT) algorithm, developed in the 1960s by Cooley and Tukey, which allows efficient calculation of discrete Fourier coefficients of a periodic function sampled on a regular grid of 2p points (or 2p3q5r with slightly reduced efficiency). 7.2 Example of the FFT Using Matlab, take the FFT of the HW1 wave height time series (length 24 × 60=25325) and plot the result (Fig. 1): load hw1 dat; zhat = fft(z); plot(abs(zhat),’x’) A few elements (the second and last, and to a lesser extent the third and the second from last) have magnitudes that stand above the noise.
    [Show full text]
  • Extended Fourier Analysis of Signals
    Dr.sc.comp. Vilnis Liepiņš Email: [email protected] Extended Fourier analysis of signals Abstract. This summary of the doctoral thesis [8] is created to emphasize the close connection of the proposed spectral analysis method with the Discrete Fourier Transform (DFT), the most extensively studied and frequently used approach in the history of signal processing. It is shown that in a typical application case, where uniform data readings are transformed to the same number of uniformly spaced frequencies, the results of the classical DFT and proposed approach coincide. The difference in performance appears when the length of the DFT is selected greater than the length of the data. The DFT solves the unknown data problem by padding readings with zeros up to the length of the DFT, while the proposed Extended DFT (EDFT) deals with this situation in a different way, it uses the Fourier integral transform as a target and optimizes the transform basis in the extended frequency set without putting such restrictions on the time domain. Consequently, the Inverse DFT (IDFT) applied to the result of EDFT returns not only known readings, but also the extrapolated data, where classical DFT is able to give back just zeros, and higher resolution are achieved at frequencies where the data has been extrapolated successfully. It has been demonstrated that EDFT able to process data with missing readings or gaps inside or even nonuniformly distributed data. Thus, EDFT significantly extends the usability of the DFT based methods, where previously these approaches have been considered as not applicable [10-45]. The EDFT founds the solution in an iterative way and requires repeated calculations to get the adaptive basis, and this makes it numerical complexity much higher compared to DFT.
    [Show full text]
  • Discretization of Integro-Differential Equations
    Discretization of Integro-Differential Equations Modeling Dynamic Fractional Order Viscoelasticity K. Adolfsson1, M. Enelund1,S.Larsson2,andM.Racheva3 1 Dept. of Appl. Mech., Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 2 Dept. of Mathematics, Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 3 Dept. of Mathematics, Technical University of Gabrovo, 5300 Gabrovo, Bulgaria Abstract. We study a dynamic model for viscoelastic materials based on a constitutive equation of fractional order. This results in an integro- differential equation with a weakly singular convolution kernel. We dis- cretize in the spatial variable by a standard Galerkin finite element method. We prove stability and regularity estimates which show how the convolution term introduces dissipation into the equation of motion. These are then used to prove a priori error estimates. A numerical ex- periment is included. 1 Introduction Fractional order operators (integrals and derivatives) have proved to be very suit- able for modeling memory effects of various materials and systems of technical interest. In particular, they are very useful when modeling viscoelastic materials, see, e.g., [3]. Numerical methods for quasistatic viscoelasticity problems have been studied, e.g., in [2] and [8]. The drawback of the fractional order viscoelastic models is that the whole strain history must be saved and included in each time step. The most commonly used algorithms for this integration are based on the Lubich convolution quadrature [5] for fractional order operators. In [1, 2], we develop an efficient numerical algorithm based on sparse numerical quadrature earlier studied in [6]. While our earlier work focused on discretization in time for the quasistatic case, we now study space discretization for the fully dynamic equations of mo- tion, which take the form of an integro-differential equation with a weakly singu- lar convolution kernel.
    [Show full text]
  • Fourier Analysis of Discrete-Time Signals
    Fourier analysis of discrete-time signals (Lathi Chapt. 10 and these slides) Towards the discrete-time Fourier transform • How we will get there? • Periodic discrete-time signal representation by Discrete-time Fourier series • Extension to non-periodic DT signals using the “periodization trick” • Derivation of the Discrete Time Fourier Transform (DTFT) • Discrete Fourier Transform Discrete-time periodic signals • A periodic DT signal of period N0 is called N0-periodic signal f[n + kN0]=f[n] f[n] n N0 • For the frequency it is customary to use a different notation: the frequency of a DT sinusoid with period N0 is 2⇡ ⌦0 = N0 Fourier series representation of DT periodic signals • DT N0-periodic signals can be represented by DTFS with 2⇡ fundamental frequency ⌦ 0 = and its multiples N0 • The exponential DT exponential basis functions are 0k j⌦ k j2⌦ k jn⌦ k e ,e± 0 ,e± 0 ,...,e± 0 Discrete time 0k j! t j2! t jn! t e ,e± 0 ,e± 0 ,...,e± 0 Continuous time • Important difference with respect to the continuous case: only a finite number of exponentials are different! • This is because the DT exponential series is periodic of period 2⇡ j(⌦ 2⇡)k j⌦k e± ± = e± Increasing the frequency: continuous time • Consider a continuous time sinusoid with increasing frequency: the number of oscillations per unit time increases with frequency Increasing the frequency: discrete time • Discrete-time sinusoid s[n]=sin(⌦0n) • Changing the frequency by 2pi leaves the signal unchanged s[n]=sin((⌦0 +2⇡)n)=sin(⌦0n +2⇡n)=sin(⌦0n) • Thus when the frequency increases from zero, the number of oscillations per unit time increase until the frequency reaches pi, then decreases again towards the value that it had in zero.
    [Show full text]
  • Fourier Analysis
    Fourier Analysis Hilary Weller <[email protected]> 19th October 2015 This is brief introduction to Fourier analysis and how it is used in atmospheric and oceanic science, for: Analysing data (eg climate data) • Numerical methods • Numerical analysis of methods • 1 1 Fourier Series Any periodic, integrable function, f (x) (defined on [ π,π]), can be expressed as a Fourier − series; an infinite sum of sines and cosines: ∞ ∞ a0 f (x) = + ∑ ak coskx + ∑ bk sinkx (1) 2 k=1 k=1 The a and b are the Fourier coefficients. • k k The sines and cosines are the Fourier modes. • k is the wavenumber - number of complete waves that fit in the interval [ π,π] • − sinkx for different values of k 1.0 k =1 k =2 k =4 0.5 0.0 0.5 1.0 π π/2 0 π/2 π − − x The wavelength is λ = 2π/k • The more Fourier modes that are included, the closer their sum will get to the function. • 2 Sum of First 4 Fourier Modes of a Periodic Function 1.0 Fourier Modes Original function 4 Sum of first 4 Fourier modes 0.5 2 0.0 0 2 0.5 4 1.0 π π/2 0 π/2 π π π/2 0 π/2 π − − − − x x 3 The first four Fourier modes of a square wave. The additional oscillations are “spectral ringing” Each mode can be represented by motion around a circle. ↓ The motion around each circle has a speed and a radius. These represent the wavenumber and the Fourier coefficients.
    [Show full text]
  • There Is Only One Fourier Transform Jens V
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 25 December 2017 doi:10.20944/preprints201712.0173.v1 There is only one Fourier Transform Jens V. Fischer * Microwaves and Radar Institute, German Aerospace Center (DLR), Germany Abstract Four Fourier transforms are usually defined, the Integral Fourier transform, the Discrete-Time Fourier transform (DTFT), the Discrete Fourier transform (DFT) and the Integral Fourier transform for periodic functions. However, starting from their definitions, we show that all four Fourier transforms can be reduced to actually only one Fourier transform, the Fourier transform in the distributional sense. Keywords Integral Fourier Transform, Discrete-Time Fourier Transform (DTFT), Discrete Fourier Transform (DFT), Integral Fourier Transform for periodic functions, Fourier series, Poisson Summation Formula, periodization trick, interpolation trick Introduction Two Important Operations The fact that “there is only one Fourier transform” actually There are two operations which are being strongly related to needs no proof. It is commonly known and often discussed in four different variants of the Fourier transform, i.e., the literature, for example in [1-2]. discretization and periodization. For any real-valued T > 0 and δ(t) being the Dirac impulse, let However frequently asked questions are: (1) What is the difference between calculating the Fourier series and the (1) Fourier transform of a continuous function? (2) What is the difference between Discrete-Time Fourier Transform (DTFT) be the function that results from a discretization of f(t) and let and Discrete Fourier Transform (DFT)? (3) When do we need which Fourier transform? and many others. The default answer (2) today to all these questions is to invite the reader to have a look at the so-called Fourier-Poisson cube, e.g.
    [Show full text]
  • Data Mining Algorithms
    Data Management and Exploration © for the original version: Prof. Dr. Thomas Seidl Jiawei Han and Micheline Kamber http://www.cs.sfu.ca/~han/dmbook Data Mining Algorithms Lecture Course with Tutorials Wintersemester 2003/04 Chapter 4: Data Preprocessing Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 2 Why Data Preprocessing? Data in the real world is dirty incomplete: lacking attribute values, lacking certain attributes of interest, or containing only aggregate data noisy: containing errors or outliers inconsistent: containing discrepancies in codes or names No quality data, no quality mining results! Quality decisions must be based on quality data Data warehouse needs consistent integration of quality data WS 2003/04 Data Mining Algorithms 4 – 3 Multi-Dimensional Measure of Data Quality A well-accepted multidimensional view: Accuracy (range of tolerance) Completeness (fraction of missing values) Consistency (plausibility, presence of contradictions) Timeliness (data is available in time; data is up-to-date) Believability (user’s trust in the data; reliability) Value added (data brings some benefit) Interpretability (there is some explanation for the data) Accessibility (data is actually available) Broad categories: intrinsic, contextual, representational, and accessibility. WS 2003/04 Data Mining Algorithms 4 – 4 Major Tasks in Data Preprocessing
    [Show full text]