DOCSLIB.ORG

Numerical Methods for Rotating Compact Objects in Modified Gravity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Numerical Methods for Rotating Compact Objects in Modified Gravity NUMERICAL METHODS FOR ROTATING COMPACT OBJECTS IN MODIFIED GRAVITY THEORIES by Andrew Patrick Kyung Sullivan A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Physics MONTANA STATE UNIVERSITY Bozeman, Montana April 2020 c COPYRIGHT by Andrew Patrick Kyung Sullivan 2020 All Rights Reserved ii DEDICATION I dedicate this to my mom, whose trips to the local library to checkout science books as a child were an enormous inspiration. iii ACKNOWLEDGEMENTS I would like to thank my advisor, Dr. Nicol´asYunes whose support and mentorship has been invaluable. Thank you for always pushing me to be the best researcher I can be. I would like to thank the members of my committee, especially my co-chair Dr. Neil Cornish for the constructive comments on my work. I would like to thank Margaret Jarrett of the MSU Physics department for her help and support. I would like to thank my friends who have supported me along the way especially Dimitry Ayzenberg whose conversations and company helped during the early years of my graduate career. Finally I would like to thank my family; my parents, my brother, and sister whose continual support has been immeasurable. iv TABLE OF CONTENTS 1. INTRODUCTION ........................................................................................1 2. SLOWLY-ROTATING NEUTRON STARS IN MASSIVE BIGRAV- ITY ...........................................................................................................12 Contribution of Authors and Co-Authors ..................................................... 12 Manuscript Information Page ...................................................................... 13 Abstract .................................................................................................... 14 Introduction............................................................................................... 14 Massive Bigravity ....................................................................................... 22 Slowly-rotating Neutron stars in Massive Bigravity within the Hartle-Thorne Approximation.......................................................... 27 Metric Tensors for Slowly-Rotating Spacetimes ..................................... 27 Neutron Star Stress-Energy Tensor....................................................... 28 Interaction Tensor ............................................................................... 29 Modified Field Equations..................................................................... 32 Recasting of Modified Field Equations.................................................. 35 Numerical Construction of Neutron Stars in Massive Bigravity...................... 36 Zeroth-Order in Rotation..................................................................... 37 Local analysis at r = 0 and r = ................................................ 37 Numerical Solutions .....................................................................1 40 First-Order in Rotation ....................................................................... 45 Local Analysis at r = 0 and r = ............................................... 45 Numerical Solution.......................................................................1 47 Conclusions and Future Directions............................................................... 49 Acknowledgments ....................................................................................... 52 3. NUMERICAL BLACK HOLE SOLUTIONS IN MODIFIED GRAV- ITY THEORIES: SPHERICAL SYMMETRY CASE...............................................................53 Contribution of Authors and Co-Authors ..................................................... 53 Manuscript Information Page ...................................................................... 54 Abstract .................................................................................................... 55 Introduction............................................................................................... 55 Numerical Methods..................................................................................... 61 Validation .................................................................................................. 62 Toy Problem ....................................................................................... 63 Schwarzschild Black Hole..................................................................... 68 Spherically Symmetric Black Holes in Scalar-Gauss-Bonnet Gravity............... 73 v TABLE OF CONTENTS { CONTINUED Action and Field equations .................................................................. 73 Linear Scalar-Gauss-Bonnet Gravity..................................................... 75 Einstein-dilaton-Gauss-Bonnet Gravity................................................. 82 Properties of Solution ................................................................................. 85 Fitting Function.................................................................................. 85 ISCO.................................................................................................. 87 Light Ring .......................................................................................... 90 Naked Singularity................................................................................ 91 Conclusions................................................................................................ 93 Acknowledgments ....................................................................................... 95 4. NUMERICAL BLACK HOLE SOLUTIONS IN MODIFIED GRAV- ITY THEORIES: AXIAL SYMMETRY CASE........................................................................96 Contribution of Authors and Co-Authors ..................................................... 96 Manuscript Information Page ...................................................................... 97 Abstract .................................................................................................... 98 Introduction............................................................................................... 98 Numerical Methods................................................................................... 105 Validation ................................................................................................ 108 Axially Symmetric Black Holes in Scalar-Gauss-Bonnet Gravity .................. 115 Action and Field equations ................................................................ 115 Linear Scalar-Gauss-Bonnet Gravity................................................... 118 Einstein-dilaton-Gauss-Bonnet Gravity............................................... 126 Properties of Solution ............................................................................... 126 Fitting Function................................................................................ 128 Marginal Stable Circular Orbits ......................................................... 134 Light Ring ........................................................................................ 135 Innermost Stable Circular Orbit......................................................... 136 Conclusions.............................................................................................. 137 Acknowledgments ..................................................................................... 138 5. CONCLUSION......................................................................................... 139 REFERENCES CITED.................................................................................. 141 APPENDICES .............................................................................................. 152 APPENDIX A : Sample Functions ............................................................ 153 vi TABLE OF CONTENTS { CONTINUED APPENDIX B : Numerical Methods.......................................................... 155 Iterative Relaxation Method in the Continuum Limit .......................... 156 Discrete Representation through Newton's Polynomials ....................... 158 Derivatives of Newton Polynomials and Discretization Error ................ 162 Minimization of the Discretization Error............................................. 164 Minimization of the Residual Vector................................................... 167 Linear System Solvers........................................................................ 168 APPENDIX C : Sample Fitting Coefficients for Spherically Symmetric Solutions ........................................................................... 169 APPENDIX D : Sample Fitting Coefficients for Axially Symmetric Solutions ........................................................................... 172 vii LIST OF TABLES Table Page C.1 Fitting Coefficients for ai;j ............................................................. 170 C.2 Fitting Coefficients for bi;j ............................................................. 171 C.3 Fitting Coefficients for ci;j ............................................................. 171 D.1 Fitting Coefficients for ai;j ............................................................. 173 viii LIST OF FIGURES Figure Page 2.1 The mass-radius relation (left) and the moment of inertia-mass relation (right) using three realistic equations of state with varying m and all other coupling parameters fixed. The mass of the star M is obtained from the mass function of the physical met- ric evaluated at
Load more

Recommended publications
  • Fast and Efficient Algorithms for Evaluating Uniform and Nonuniform
    World Academy of Science, Engineering and Technology International Journal of Computer and Information Engineering Vol:13, No:8, 2019 Fast and Efficient Algorithms for Evaluating Uniform and Nonuniform Lagrange and Newton Curves Taweechai Nuntawisuttiwong, Natasha Dejdumrong Abstract—Newton-Lagrange Interpolations are widely used in quadratic computation time, which is slower than the others. numerical analysis. However, it requires a quadratic computational However, there are some curves in CAGD, Wang-Ball, DP time for their constructions. In computer aided geometric design and Dejdumrong curves with linear complexity. In order to (CAGD), there are some polynomial curves: Wang-Ball, DP and Dejdumrong curves, which have linear time complexity algorithms. reduce their computational time, Bezier´ curve is converted Thus, the computational time for Newton-Lagrange Interpolations into any of Wang-Ball, DP and Dejdumrong curves. Hence, can be reduced by applying the algorithms of Wang-Ball, DP and the computational time for Newton-Lagrange interpolations Dejdumrong curves. In order to use Wang-Ball, DP and Dejdumrong can be reduced by converting them into Wang-Ball, DP and algorithms, first, it is necessary to convert Newton-Lagrange Dejdumrong algorithms. Thus, it is necessary to investigate polynomials into Wang-Ball, DP or Dejdumrong polynomials. In this work, the algorithms for converting from both uniform and the conversion from Newton-Lagrange interpolation into non-uniform Newton-Lagrange polynomials into Wang-Ball, DP and the curves with linear complexity, Wang-Ball, DP and Dejdumrong polynomials are investigated. Thus, the computational Dejdumrong curves. An application of this work is to modify time for representing Newton-Lagrange polynomials can be reduced sketched image in CAD application with the computational into linear complexity.
    [Show full text]
  • Mials P
    Euclid's Algorithm 171 Euclid's Algorithm Horner’s method is a special case of Euclid's Algorithm which constructs, for given polyno- mials p and h =6 0, (unique) polynomials q and r with deg r<deg h so that p = hq + r: For variety, here is a nonstandard discussion of this algorithm, in terms of elimination. Assume that d h(t)=a0 + a1t + ···+ adt ;ad =06 ; and n p(t)=b0 + b1t + ···+ bnt : Then we seek a polynomial n−d q(t)=c0 + c1t + ···+ cn−dt for which r := p − hq has degree <d. This amounts to the square upper triangular linear system adc0 + ad−1c1 + ···+ a0cd = bd adc1 + ad−1c2 + ···+ a0cd+1 = bd+1 . adcn−d−1 + ad−1cn−d = bn−1 adcn−d = bn for the unknown coefficients c0;:::;cn−d which can be uniquely solved by back substitution since its diagonal entries all equal ad =0.6 19aug02 c 2002 Carl de Boor 172 18. Index Rough index for these notes 1-1:-5,2,8,40 cartesian product: 2 1-norm: 79 Cauchy(-Bunyakovski-Schwarz) 2-norm: 79 Inequality: 69 A-invariance: 125 Cauchy-Binet formula: -9, 166 A-invariant: 113 Cayley-Hamilton Theorem: 133 absolute value: 167 CBS Inequality: 69 absolutely homogeneous: 70, 79 Chaikin algorithm: 139 additive: 20 chain rule: 153 adjugate: 164 change of basis: -6 affine: 151 characteristic function: 7 affine combination: 148, 150 characteristic polynomial: -8, 130, 132, 134 affine hull: 150 circulant: 140 affine map: 149 codimension: 50, 53 affine polynomial: 152 coefficient vector: 21 affine space: 149 cofactor: 163 affinely independent: 151 column map: -6, 23 agrees with y at Λt:59 column space: 29 algebraic dual: 95 column
    [Show full text]
  • CS321-001 Introduction to Numerical Methods
    CS321-001 Introduction to Numerical Methods Lecture 3 Interpolation and Numerical Differentiation Professor Jun Zhang Department of Computer Science University of Kentucky Lexington, KY 40506-0633 Polynomial Interpolation Given a set of discrete values, how can we estimate other values between these data The method that we will use is called polynomial interpolation. We assume the data we had are from the evaluation of a smooth function. We may be able to use a polynomial p(x) to approximate this function, at least locally. A condition: the polynomial p(x) takes the given values at the given points (nodes), i.e., p(xi) = yi with 0 ≤ i ≤ n. The polynomial is said to interpolate the table, since we do not know the function. 2 Polynomial Interpolation Note that all the points are passed through by the curve 3 Polynomial Interpolation We do not know the original function, the interpolation may not be accurate 4 Order of Interpolating Polynomial A polynomial of degree 0, a constant function, interpolates one set of data If we have two sets of data, we can have an interpolating polynomial of degree 1, a linear function x x1 x x0 p(x) y0 y1 x0 x1 x1 x0 y1 y0 y0 (x x0 ) x1 x0 Review carefully if the interpolation condition is satisfied Interpolating polynomials can be written in several forms, the most well known ones are the Lagrange form and Newton form. Each has some advantages 5 Lagrange Form For a set of fixed nodes x0, x1, …, xn, the cardinal functions, l0, l1,…, ln, are defined as 0 if i j li (x j ) ij
    [Show full text]
  • Gravity's Fatal Attraction
    Cambridge University Press 978-0-521-71793-9 - Gravity’s Fatal Attraction: Black Holes in the Universe, Second Edition Mitchell Begelman and Martin Rees Frontmatter More information GRAVITY’S FATAL ATTRACTION Black Holes in the Universe Second edition Richly illustrated with the images from observatories on the ground and in space, and computer simulations, this book shows how black holes were discovered, and discusses our current understanding of their role in cosmic evolution. This second edition covers new discoveries made in the past decade, including defi nitive proof of a black hole at the center of the Milky Way, evidence that the expansion of the Universe is accelerating, and the new appreciation of the connection between black holes and galaxy formation. There are entirely new chapters on gamma-ray bursts and cosmic feedback. Begelman and Rees blend theoretical arguments with observa- tional results to demonstrate how both have contributed to the subject. Clear, explanatory illustrations and photographs reveal the strange and amazing workings of our Universe. The engaging style makes this book suitable for introductory undergraduate courses, amateur astronomers, and all readers interested in astronomy and physics. Mitchell Begelman is Chairman of the Department of Astrophysical and Planetary Sciences and Fellow of JILA, at the University of Colorado at Boulder. He has won several awards, including the Guggenheim Fel- lowship, Sloan Research Fellowship, and the American Astronomical Society Warner Prize. Martin Rees is Professor of Cosmology and Astrophysics and Master of Trinity College at Cambridge University, and Astronomer Royal. He is a winner of the Gold Medal of the Royal Astronomical Society and other awards.
    [Show full text]
  • 10. Scientific Programme 10.1
    10. SCIENTIFIC PROGRAMME 10.1. OVERVIEW (a) Invited Discourses Plenary Hall B 18:00-19:30 ID1 “The Zoo of Galaxies” Karen Masters, University of Portsmouth, UK Monday, 20 August ID2 “Supernovae, the Accelerating Cosmos, and Dark Energy” Brian Schmidt, ANU, Australia Wednesday, 22 August ID3 “The Herschel View of Star Formation” Philippe André, CEA Saclay, France Wednesday, 29 August ID4 “Past, Present and Future of Chinese Astronomy” Cheng Fang, Nanjing University, China Nanjing Thursday, 30 August (b) Plenary Symposium Review Talks Plenary Hall B (B) 8:30-10:00 Or Rooms 309A+B (3) IAUS 288 Astrophysics from Antarctica John Storey (3) Mon. 20 IAUS 289 The Cosmic Distance Scale: Past, Present and Future Wendy Freedman (3) Mon. 27 IAUS 290 Probing General Relativity using Accreting Black Holes Andy Fabian (B) Wed. 22 IAUS 291 Pulsars are Cool – seriously Scott Ransom (3) Thu. 23 Magnetars: neutron stars with magnetic storms Nanda Rea (3) Thu. 23 Probing Gravitation with Pulsars Michael Kremer (3) Thu. 23 IAUS 292 From Gas to Stars over Cosmic Time Mordacai-Mark Mac Low (B) Tue. 21 IAUS 293 The Kepler Mission: NASA’s ExoEarth Census Natalie Batalha (3) Tue. 28 IAUS 294 The Origin and Evolution of Cosmic Magnetism Bryan Gaensler (B) Wed. 29 IAUS 295 Black Holes in Galaxies John Kormendy (B) Thu. 30 (c) Symposia - Week 1 IAUS 288 Astrophysics from Antartica IAUS 290 Accretion on all scales IAUS 291 Neutron Stars and Pulsars IAUS 292 Molecular gas, Dust, and Star Formation in Galaxies (d) Symposia –Week 2 IAUS 289 Advancing the Physics of Cosmic
    [Show full text]
  • 277 — 18 January 2016 Editor: Bo Reipurth ([email protected]) List of Contents
    THE STAR FORMATION NEWSLETTER An electronic publication dedicated to early stellar/planetary evolution and molecular clouds No. 277 — 18 January 2016 Editor: Bo Reipurth ([email protected]) List of Contents The Star Formation Newsletter Interview ...................................... 3 Abstracts of Newly Accepted Papers ........... 5 Editor: Bo Reipurth [email protected] Abstracts of Newly Accepted Major Reviews . 30 Technical Editor: Eli Bressert Dissertation Abstracts ........................ 31 [email protected] New Jobs ..................................... 32 Technical Assistant: Hsi-Wei Yen Meetings ..................................... 33 [email protected] Summary of Upcoming Meetings ............. 36 Editorial Board Joao Alves Alan Boss Jerome Bouvier Cover Picture Lee Hartmann Thomas Henning The Rosette Nebula is a large HII region in Mono- Paul Ho ceros at a distance of about 1.6 - 1.7 kpc. It is Jes Jorgensen illuminated by the OB cluster NGC 2244, which Charles J. Lada contains seven O-stars, dominated by the O4V star Thijs Kouwenhoven HD 46223. The northwestern edge of the HII region Michael R. Meyer contains a large complex of globules and elephant Ralph Pudritz trunks. Luis Felipe Rodr´ıguez Ewine van Dishoeck Image courtesy Don Goldman http://astrodonimaging.com Hans Zinnecker ( ). The Star Formation Newsletter is a vehicle for fast distribution of information of interest for as- tronomers working on star and planet formation and molecular clouds. You can submit material for the following sections: Abstracts of recently Submitting your abstracts accepted papers (only for papers sent to refereed journals), Abstracts of recently accepted major re- Latex macros for submitting abstracts views (not standard conference contributions), Dis- and dissertation abstracts (by e-mail to sertation Abstracts (presenting abstracts of new [email protected]) are appended to Ph.D dissertations), Meetings (announcing meet- each Call for Abstracts.
    [Show full text]
  • Lagrange & Newton Interpolation
    Lagrange & Newton interpolation In this section, we shall study the polynomial interpolation in the form of Lagrange and Newton. Given a se- quence of (n +1) data points and a function f, the aim is to determine an n-th degree polynomial which interpol- ates f at these points. We shall resort to the notion of divided differences. Interpolation Given (n+1) points {(x0, y0), (x1, y1), …, (xn, yn)}, the points defined by (xi)0≤i≤n are called points of interpolation. The points defined by (yi)0≤i≤n are the values of interpolation. To interpolate a function f, the values of interpolation are defined as follows: yi = f(xi), i = 0, …, n. Lagrange interpolation polynomial The purpose here is to determine the unique polynomial of degree n, Pn which verifies Pn(xi) = f(xi), i = 0, …, n. The polynomial which meets this equality is Lagrange interpolation polynomial n Pnx=∑ l j x f x j j=0 where the lj ’s are polynomials of degree n forming a basis of Pn n x−xi x−x0 x−x j−1 x−x j 1 x−xn l j x= ∏ = ⋯ ⋯ i=0,i≠ j x j −xi x j−x0 x j−x j−1 x j−x j1 x j−xn Properties of Lagrange interpolation polynomial and Lagrange basis They are the lj polynomials which verify the following property: l x = = 1 i= j , ∀ i=0,...,n. j i ji {0 i≠ j They form a basis of the vector space Pn of polynomials of degree at most equal to n n ∑ j l j x=0 j=0 By setting: x = xi, we obtain: n n ∑ j l j xi =∑ j ji=0 ⇒ i =0 j=0 j=0 The set (lj)0≤j≤n is linearly independent and consists of n + 1 vectors.
    [Show full text]
  • Mathematical Topics
    A Mathematical Topics This chapter discusses most of the mathematical background needed for a thor­ ough understanding of the material presented in the book. It has been mentioned in the Preface, however, that math concepts which are only used once (such as the mediation operator and points vs. vectors) are discussed right where they are introduced. Do not worry too much about your difficulties in mathematics, I can assure you that mine a.re still greater. - Albert Einstein. A.I Fourier Transforms Our curves are functions of an arbitrary parameter t. For functions used in science and engineering, time is often the parameter (or the independent variable). We, therefore, say that a function g( t) is represented in the time domain. Since a typical function oscillates, we can think of it as being similar to a wave and we may try to represent it as a wave (or as a combination of waves). When this is done, we have the function G(f), where f stands for the frequency of the wave, and we say that the function is represented in the frequency domain. This turns out to be a useful concept, since many operations on functions are easy to carry out in the frequency domain. Transforming a function between the time and frequency domains is easy when the function is periodic, but it can also be done for certain non periodic functions. The present discussion is restricted to periodic functions. 1IIIt Definition: A function g( t) is periodic if (and only if) there exists a constant P such that g(t+P) = g(t) for all values of t (Figure A.la).
    [Show full text]
  • FY 2017 Annual Report July 1, 2016 – June 30, 2017
    FY 2017 Annual Report July 1, 2016 – June 30, 2017 A supporting organization of A. Sarah Hreha, Executive Director The Gruber Foundation November 20, 2017 [email protected] The Gruber Foundation FY 2017 Report 1 Executive Summary The Gruber Foundation honors individuals in the fields of Cosmology, Genetics, Neuroscience, Justice, and Women's Rights, whose groundbreaking work provides new models that inspire and enable fundamental shifts in knowledge and culture. The Gruber Foundation is a 509(a)(3) Type 1 supporting organization operated, supervised, or controlled by Yale University and incorporated in 2011 under the 501(c)(3) section of U.S. Corporate Law. It was funded by The Peter and Patricia Gruber Foundation, and Peter and Patricia Gruber were its Co-founders. As President Emeritus, Patricia Gruber A. Sarah Hreha, Executive Director has a lifetime seat on the Board. The Foundation ended its sixth year at Yale with the second Gruber Symposium organized by and for Gruber Science Fellows, in May 2016. Participants ranged from the life sciences to Astronomy, and within fields the topics varied. The third annual Gruber Cosmology Conference at Yale was held in October, and included Kip Thorne and Rainer Weiss, two of the 2016 Cosmology Prize co-recipients, and was attended by over 100 students, faculty and staff. The 2016 Gruber International Prizes were awarded in New York City, Vancouver, Canada, and San Diego, CA. The Prize events are staffed by Gruber Science Fellows in the respective disciplines who generously volunteer to help us honor our recipients. In addition to more mundane logistical tasks, they each have a minute or two to describe their research to a group comprising mostly eminent scientists – their future colleagues.
    [Show full text]
  • A Low‐Cost Solution to Motion Tracking Using an Array of Sonar Sensors and An
    A Low‐cost Solution to Motion Tracking Using an Array of Sonar Sensors and an Inertial Measurement Unit A thesis presented to the faculty of the Russ College of Engineering and Technology of Ohio University In partial fulfillment of the requirements for the degree Master of Science Jason S. Maxwell August 2009 © 2009 Jason S. Maxwell. All Rights Reserved. 2 This thesis titled A Low‐cost Solution to Motion Tracking Using an Array of Sonar Sensors and an Inertial Measurement Unit by JASON S. MAXWELL has been approved for the School of Electrical Engineering Computer Science and the Russ College of Engineering and Technology by Maarten Uijt de Haag Associate Professor School of Electrical Engineering and Computer Science Dennis Irwin Dean, Russ College of Engineering and Technology 3 ABSTRACT MAXWELL, JASON S., M.S., August 2009, Electrical Engineering A Low‐cost Solution to Motion Tracking Using an Array of Sonar Sensors and an Inertial Measurement Unit (91 pp.) Director of Thesis: Maarten Uijt de Haag As the desire and need for unmanned aerial vehicles (UAV) increases, so to do the navigation and system demands for the vehicles. While there are a multitude of systems currently offering solutions, each also possess inherent problems. The Global Positioning System (GPS), for instance, is potentially unable to meet the demands of vehicles that operate indoors, in heavy foliage, or in urban canyons, due to the lack of signal strength. Laser‐based systems have proven to be rather costly, and can potentially fail in areas in which the surface absorbs light, and in urban environments with glass or mirrored surfaces.
    [Show full text]
  • The AMATYC Review, Fall 1992-Spring 1993. INSTITUTION American Mathematical Association of Two-Year Colleges
    DOCUMENT RESUME ED 354 956 JC 930 126 AUTHOR Cohen, Don, Ed.; Browne, Joseph, Ed. TITLE The AMATYC Review, Fall 1992-Spring 1993. INSTITUTION American Mathematical Association of Two-Year Colleges. REPORT NO ISSN-0740-8404 PUB DATE 93 NOTE 203p. AVAILABLE FROMAMATYC Treasurer, State Technical Institute at Memphis, 5983 Macon Cove, Memphis, TN 38134 (for libraries 2 issues free with $25 annual membership). PUB TYPE Collected Works Serials (022) JOURNAL CIT AMATYC Review; v14 n1-2 Fall 1992-Spr 1993 EDRS PRICE MF01/PC09 Plus Postage. DESCRIPTORS *College Mathematics; Community Colleges; Computer Simulation; Functions (Mathematics); Linear Programing; *Mathematical Applications; *Mathematical Concepts; Mathematical Formulas; *Mathematics Instruction; Mathematics Teachers; Technical Mathematics; Two Year Colleges ABSTRACT Designed as an avenue of communication for mathematics educators concerned with the views, ideas, and experiences of two-year collage students and teachers, this journal contains articles on mathematics expoition and education,as well as regular features presenting book and software reviews and math problems. The first of two issues of volume 14 contains the following major articles: "Technology in the Mathematics Classroom," by Mike Davidson; "Reflections on Arithmetic-Progression Factorials," by William E. Rosentl,e1; "The Investigation of Tangent Polynomials with a Computer Algebra System," by John H. Mathews and Russell W. Howell; "On Finding the General Term of a Sequence Using Lagrange Interpolation," by Sheldon Gordon and Robert Decker; "The Floating Leaf Problem," by Richard L. Francis; "Approximations to the Hypergeometric Distribution," by Chltra Gunawardena and K. L. D. Gunawardena; aid "Generating 'JE(3)' with Some Elementary Applications," by John J. Edgeli, Jr. The second issue contains: "Strategies for Making Mathematics Work for Minorities," by Beverly J.
    [Show full text]
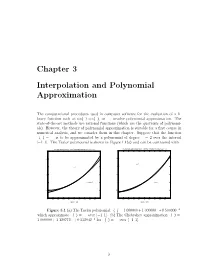
  • Chapter 3 Interpolation and Polynomial Approximation
    Chapter 3 Interpolation and Polynomial Approximation The computational procedures used in computer software for the evaluation of a li- brary function such as sin(x); cos(x), or ex, involve polynomial approximation. The state-of-the-art methods use rational functions (which are the quotients of polynomi- als). However, the theory of polynomial approximation is suitable for a first course in numerical analysis, and we consider them in this chapter. Suppose that the function f(x) = ex is to be approximated by a polynomial of degree n = 2 over the interval [¡1; 1]. The Taylor polynomial is shown in Figure 1.1(a) and can be contrasted with 2 x The Taylor polynomial p(x)=1+x+0.5x2 which approximates f(x)=ex over [−1,1] The Chebyshev approximation q(x)=1+1.129772x+0.532042x for f(x)=e over [−1,1] 3 3 2.5 2.5 y=ex 2 2 y=ex 1.5 1.5 2 1 y=1+x+0.5x 1 y=q(x) 0.5 0.5 0 0 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Figure 1.1(a) Figure 1.1(b) Figure 3.1 (a) The Taylor polynomial p(x) = 1:000000+ 1:000000x +0:500000x2 which approximate f(x) = ex over [¡1; 1]. (b) The Chebyshev approximation q(x) = 1:000000 + 1:129772x + 0:532042x2 for f(x) = ex over [¡1; 1].
    [Show full text]