Empirical Bayes Ranking with R-Values
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Rosters Set for 2014-15 Nba Regular Season
ROSTERS SET FOR 2014-15 NBA REGULAR SEASON NEW YORK, Oct. 27, 2014 – Following are the opening day rosters for Kia NBA Tip-Off ‘14. The season begins Tuesday with three games: ATLANTA BOSTON BROOKLYN CHARLOTTE CHICAGO Pero Antic Brandon Bass Alan Anderson Bismack Biyombo Cameron Bairstow Kent Bazemore Avery Bradley Bojan Bogdanovic PJ Hairston Aaron Brooks DeMarre Carroll Jeff Green Kevin Garnett Gerald Henderson Mike Dunleavy Al Horford Kelly Olynyk Jorge Gutierrez Al Jefferson Pau Gasol John Jenkins Phil Pressey Jarrett Jack Michael Kidd-Gilchrist Taj Gibson Shelvin Mack Rajon Rondo Joe Johnson Jason Maxiell Kirk Hinrich Paul Millsap Marcus Smart Jerome Jordan Gary Neal Doug McDermott Mike Muscala Jared Sullinger Sergey Karasev Jannero Pargo Nikola Mirotic Adreian Payne Marcus Thornton Andrei Kirilenko Brian Roberts Nazr Mohammed Dennis Schroder Evan Turner Brook Lopez Lance Stephenson E'Twaun Moore Mike Scott Gerald Wallace Mason Plumlee Kemba Walker Joakim Noah Thabo Sefolosha James Young Mirza Teletovic Marvin Williams Derrick Rose Jeff Teague Tyler Zeller Deron Williams Cody Zeller Tony Snell INACTIVE LIST Elton Brand Vitor Faverani Markel Brown Jeffery Taylor Jimmy Butler Kyle Korver Dwight Powell Cory Jefferson Noah Vonleh CLEVELAND DALLAS DENVER DETROIT GOLDEN STATE Matthew Dellavedova Al-Farouq Aminu Arron Afflalo Joel Anthony Leandro Barbosa Joe Harris Tyson Chandler Darrell Arthur D.J. Augustin Harrison Barnes Brendan Haywood Jae Crowder Wilson Chandler Caron Butler Andrew Bogut Kentavious Caldwell- Kyrie Irving Monta Ellis -

Atlanta Hawks Re-Sign Mike Muscala
FOR IMMEDIATE RELEASE: 7/25/17 CONTACT: Garin Narain, Jon Steinberg or Jason Roose, Hawks Media Relations (404) 878-3800 ATLANTA HAWKS RE-SIGN MIKE MUSCALA ATLANTA, GA – The Atlanta Hawks Basketball Club has re-signed forward Mike Muscala, it was announced today by General Manager and Head of Basketball Operations Travis Schlenk. Per team policy, terms of the agreement were not disclosed. Last season in 70 games (three starts) with the Hawks, Muscala averaged career-highs of 6.2 points, 3.4 rebounds and 1.4 assists in 17.7 minutes (.504 FG%, .418 3FG%, .766 FT%). He scored in double figures 20 times, ranking second on the club in FG% and fifth in rpg. “Mike is a valuable player for us and a great fit both on and off the floor,” Schlenk said. “He’s worked hard and improved each year, and we’re very happy he’ll continue his career with the Hawks.” In 190 career contests (11 starting assignments) in four years with Atlanta, the 6’11 forward/center is averaging 4.8 points and 2.8 rebounds in 13.3 minutes (.505 FG%, .385 3FG%, .817 FT%), also appearing in 27 postseason games. Muscala was the recipient of the 2016 Jason Collier Memorial Trophy, presented to the player who best exemplifies the characteristics that Collier displayed off the court as a community ambassador. Originally acquired by the Hawks on June 28, 2013, along with the draft rights to Lucas Nogueira and Jared Cunningham from Dallas, in exchange for the draft rights to Shane Larkin, Muscala was the 44 th overall pick by the Mavericks in the 2013 NBA Draft. -
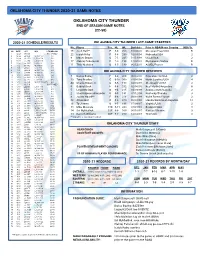
Thunder 2020-21 Game Notes
OKLAHOMA CITY THUNDER 2020-21 GAME NOTES OKLAHOMA CITY THUNDER END OF SEASON GAME NOTES (22-50) 2020-21 SCHEDULE/RESULTS OKLAHOMA CITY THUNDER LAST GAME STARTERS No. Player Pos. Ht. Wt. Birthdate Prior to NBA/Home Country NBA Yr. NO DATE OPP W/L **TV/RECORD 15 Josh Hall** F 6-8 200 10/08/00 Moravian Prep/USA R 1 12/23 @ HOU POSTPONED 22 Isaiah Roby F 6-8 230 02/03/98 Nebraska/USA 2 2 12/26 @ CHA W, 109-107 1-0 9 Moses Brown C 7-1 245 10/13/99 UCLA/USA 2 3 12/28 vs. UTA L, 109-110 1-1 4 12/29 vs. ORL L, 107-118 1-2 17 Aleksej Pokuševski F 7-0 195 12/26/01 Olympiacos/Serbia R 5 12/31 vs. NOP L, 80-113 1-3 6 1/2 @ ORL W, 108-99 2-3 11 Théo Maledon G 6-5 180 06/12/01 ASVEL/France R 7 1/4 @ MIA L, 90-118 2-4 8 1/6 @ NOP W, 111-110 3-4 OKLAHOMA CITY THUNDER RESERVES 9 1/8 @ NYK W, 101-89 4-4 10 1/10 @ BKN W, 129-116 5-4 11 1/12 vs. SAS L, 102-112 5-5 7 Darius Bazley F 6-8 208 06/12/00 Princeton HS/USA 2 12 1/13 vs. LAL L, 99-128 5-6 13 Tony Bradley C 6-10 260 01/08/98 North Carolina/USA 4 13 1/15 vs. CHI W, 127-125 (OT) 6-6 44 Charlie Brown Jr. -

2013 NBA Draft
Round 1 Draft Picks 1. Cleveland Cavaliers – Anthony Bennett (PF), UNLV 2. Orlando Magic – Victor Oladipo (SG), Indiana 3. Washington Wizards – Otto Porter Jr. (SF), Georgetown 4. Charlotte Bobcats – Cody Zeller (PF), Indiana University 5. Phoenix Suns – Alex Len (C), Maryland 6. New Orleans Pelicans – Nerlens Noel (C), Kentucky 7. Sacramento KinGs – Ben McLemore (SG), Kansas 8. Detroit Pistons – Kentavious Caldwell-Pope (SG), Georgia 9. Minnesota Timberwolves – Trey Burke (PG), Michigan 10. Portland Trail Blazers – C.J. McCollum (PG), Lehigh 11. Philadelphia 76ers – Michael Carter-Williams (PG), Syracuse 12. Oklahoma City Thunder – Steven Adams (C), PittsburGh 13. Dallas Mavericks – Kelly Olynyk (PF), Gonzaga 14. Utah Jazz – Shabazz Muhammad (SF), UCLA 15. Milwaukee Bucks – Giannis Antetokounmpo (SF), Greece 16. Boston Celtics – Lucas Nogueira (C), Brazil 17. Atlanta Hawks – Dennis Schroeder (PG), Germany 18. Atlanta Hawks – Shane Larkin (PG), Miami 19. Cleveland Cavaliers – Sergey Karasev (SG), Russia 20. ChicaGo Bulls – Tony Snell (SF), New Mexico 21. Utah Jazz – Gorgui Dieng (C), Louisville 22. Brooklyn – Mason Plumlee, (C), Duke 23. Indiana Pacers – Solomon Hill (SF), Arizona 24. New York Knicks – Tim Hardaway Jr. (SG), MichiGan 25. Los Angeles Clippers – Reggie Bullock (SG), UNC 26. Minnesota Timberwolves – Andre Roberson (SF), Colorado 27. Denver Nuggets – Rudy Gobert (SF), France 28. San Antonio Spurs – Livio Jean-Charles (PF), French Guiana 29. Oklahoma City Thunder – Archie Goodwin (SG), Kentucky 30. Phoenix Suns – Nemanja Nedovic (SG), Serbia Round 2 Draft Picks 31. Cleveland Cavaliers – Allen Crabbe (SG), California 32. Oklahoma City Thunder – Alex Abrines (SG), Spain 33. Cleveland Cavaliers – Carrick Felix (SG), Arizona State 34. Houston Rockets – Isaiah Canaan (PG), Murray State 35. -

Division I Men's Basketball Records
DIVISION I MEN’S BASKETBALL RECORDS Individual Records 2 Team Records 5 All-Time Individual Leaders 10 Career Records 21 Top 10 Individual Scoring Leaders 30 Annual Individual Champions 38 Miscellaneous Player Information 44 All-Time Team Leaders 46 Annual Team Champions 62 Statistical Trends 73 All-Time Winningest Schools 75 Vacated and Forfeited Games 80 Winningest Schools by Decade 83 Winningest Schools Over Periods of Time 88 Winning Streaks 92 Rivalries 94 Associated Press (AP) Poll Records 97 Week-by-Week AP Polls 113 Week-by-Week Coaches Polls 166 Final Season Polls National Polls 220 INDIVIDUAL RECORDS Basketball records are confined to the “modern Points by one Player for era,” which began with the 1937-38 season, FIELD GOALS the first without the center jump after each goal all his Team’s Points in scored. Except for the school’s all-time won- lost record or coaches’ records, only statistics a Half Field Goals achieved while an institution was an active mem- 17—Brian Wardle, Marquette vs. DePaul, Feb. 16, 2000 (17-27 halftime score) Game ber of the NCAA are included in team or individual 41—Frank Selvy, Furman vs. Newberry, Feb. categories. Official weekly statistics rankings in Points in 30 Seconds or 13, 1954 (66 attempts) scoring and shooting began with the 1947-48 Season season; individual rebounds were added for the Less 522—Pete Maravich, LSU, 1970 (1,168 1950-51 season, although team rebounds were 11—Marvin O’Connor, Saint Joseph’s vs. La attempts) not added until 1954-55. Individual assists were Salle, Mar. -

The Automated General Manager
An Unbiased, Backtested Algorithmic System for Drafts, Trades, and Free Agency that The Automated Outperforms Human Front Oices Philip Maymin University of Bridgeport Vantage Sports Trefz School of Business [email protected] [email protected] General Manager All tools and reports available for free on nbagm.pm Draft Performance 200315 of All Picks Evaluate: Kawhi Leonard 2015 NBA Draft Board Production measured as average Wins Made (WM) over irst three seasons. Player Drafted Team Projection RSCI 54 Reach 106 Height 79 ORB% 11.80 Min/3PFGA 12.74 # 1 D’Angelo Russell 2 LAL 5.422 nbnMock 9 MaxVert 32.00 Weight 230 DRB% 27.60 FT/FGA 0.30 Pick 15 Pick 615 Pick 1630 Pick 3145 Pick 4660 2 Karl Anthony Towns 1 MIN 5.125 Actual: 3.94 Actual: 2.02 Actual: 1.24 Actual: 0.53 Actual: 0.28 deMock Sprint SoS AST% PER 14 3.15 0.56 15.80 27.50 3 Jahlil Okafor 3 PHL 5.113 Model: 4.64 Model: 3.88 Model: 2.75 Model: 1.42 Model: 0.50 $Gain: +3.49 $Gain: +9.18 $Gain: +7.51 $Gain: +4.42 $Gain: +1.08 sbMock 8 Agility 11.45 Pos F TOV% 12.40 PPS 1.20 4 Willie Cauley-Stein 6 SAC 3.297 5 Frank Kaminsky 9 CHA 3.077 cfMock 7 Bench 3 Age 19.96 STL% 2.90 ORtg 112.90 In this region, the model draft choice was 6 Justise Winslow 10 MIA 2.916 siMock 7 Body Fat 5.40 GP 36 BLK% 2.00 DRtg 85.90 6 substantially better, by at least one win. -
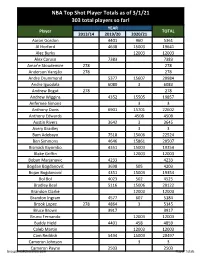
NBA Top Shot Checklist 2020-21
NBA Top Shot Player Totals as of 3/1/21 303 total players so far! YEAR Player TOTAL 2013/14 2019/20 2020/21 Aaron Gordon 4401 960 5361 Al Horford 4638 15003 19641 Alec Burks 12003 12003 Alex Caruso 7383 7383 Amar'e Stoudemire 278 278 Anderson Varejão 278 278 Andre Drummond 5377 15607 20984 Andre Iguodala 6080 3 6083 Andrew Bogut 278 278 Andrew Wiggins 4352 15505 19857 Anfernee Simons 3 3 Anthony Davis 6901 15701 22602 Anthony Edwards 4508 4508 Austin Rivers 3642 3 3645 Avery Bradley 3 3 Bam Adebayo 7518 15006 22524 Ben Simmons 4646 15861 20507 Bismack Biyombo 4351 15003 19354 Blake Griffin 12003 12003 Boban Marjanovic 4233 4233 Bogdan Bogdanović 3698 505 4203 Bojan Bogdanović 4351 15003 19354 Bol Bol 4023 502 4525 Bradley Beal 5116 15006 20122 Brandon Clarke 12003 12003 Brandon Ingram 4577 607 5184 Brook Lopez 278 4864 3 5145 Bruce Brown 3917 3917 Bruno Fernando 12003 12003 Buddy Hield 4401 458 4859 Caleb Martin 12003 12003 Cam Reddish 5494 15003 20497 Cameron Johnson 3 3 Cameron Payne 2503 2503 GroupBreakChecklists.com Player Totals YEAR Player TOTAL 2013/14 2019/20 2020/21 Caris LeVert 5798 5505 11303 Carmelo Anthony 278 4501 15610 20389 Cedi Osman 4351 3 4354 Chauncey Billups 278 278 Chris Bosh 278 278 Chris Boucher 12006 12006 Chris Paul 278 4866 15359 20503 Christian Wood 3642 15006 18648 Chuma Okeke 3 3 CJ McCollum 4352 9396 13748 Clint Capela 37006 37006 Coby White 5160 15105 20265 Cody Zeller 4221 3 4224 Cole Anthony 4006 4006 Collin Sexton 5677 25505 31182 Damian Lillard 6081 22509 28590 Damion Lee 2503 3 2506 D'Angelo Russell 5983 23894 29877 Daniel Theis 5982 15003 20985 Danilo Gallinari 4297 4297 Danny Granger 278 278 Danny Green 4910 3 4913 Danuel House Jr. -

2017 Atlanta Hawks Playoff Media Guide
TABLE OF CONTENTS 2017 PLAYOFF INFORMATION PR Contacts................................................................1 Media Information ......................................................2 Hawks vs. Washington Wizards Information ..............3 2016 Hawks Playoff Stats ..........................................6 BIOS Mike Budenholzer ......................................................7 Playoff Roster..............................................................8 Kent Bazemore ..........................................................9 DeAndre’ Bembry......................................................11 Jose Calderon ..........................................................13 Malcolm Delaney ......................................................15 Mike Dunleavy..........................................................17 Tim Hardaway Jr. ....................................................19 Dwight Howard ........................................................21 Kris Humphries ........................................................23 Ersan Ilyasova ..........................................................25 Ryan Kelly ................................................................27 Paul Millsap..............................................................29 Mike Muscala ..........................................................31 Taurean Prince ........................................................33 Dennis Schröder ......................................................35 Thabo Sefolosha ......................................................37 -

Lista Dei Giocatori Disponibili
FANTA NBA 2015/2016: LISTA DEI GIOCATORI DISPONIBILI ATLANTA HAWKS Rondae Hollis-Jefferson A Iman Shumpert G Danilo Gallinari A Festus Ezeli C Lance Stephenson G Dennis Schroder G Thaddeus Young A J.R. Smith G Darrell Arthur A Marreese Speights C Pablo Prigioni G Jeff Teague G Thomas Robinson A James Jones G Devin Sweetney A Wesley Johnson G Justin Holiday G Willie Reed A Jared Cunningham G J.J. Hickson A HOUSTON ROCKETS Blake Griffin A Kent Bazemore G Andrea Bargnani C Joe Harris G Joffrey Lauvergne A Corey Brewer G Branden Dawson A Kyle Korver G Brook Lopez C Kyrie Irving G Kenneth Faried A Denzel Livingston G Chuck Hayes A Lamar Patterson G Matthew Dellavedova G Wilson Chandler A James Harden G Josh Smith A Shelvin Mack G CHARLOTTE BOBCATS Mo Williams G Jusuf Nurkic C Jason Terry G Luc Richard Mbah a Moute A Terran Petteway G Aaron Harrison G Quinn Cook G Nikola Jokic C K.J. McDaniels G Paul Pierce A Thabo Sefolosha G Brian Roberts G Anderson Varejao A Oleksiy Pecherov C Marcus Thornton G Cole Aldrich C Tim Hardaway Jr. G Damien Wilkins G Austin Daye A Patrick Beverley G DeAndre Jordan C Al Horford A Elliot Williams G Jack Cooley A DETROIT PISTONS Ty Lawson G DeQuan Jones A Jeremy Lamb G Kevin Love A Adonis Thomas G Will Cummings G LOS ANGELES LAKERS Mike Muscala A Jeremy Lin G LeBron James A Brandon Jennings G Arsalan Kazemi A D'Angelo Russell G Mike Scott A Kemba Walker G Nick Minnerath A Jodie Meeks G Chris Walker A Jabari Brown G Paul Millsap A P.J. -

Atlanta Hawks Pay It Forward at Local Dunkin' Donuts Restaurants
FOR IMMEDIATE RELEASE: 10/24/14 CONTACT: Garin Narain or Jelani Downing, Hawks Corporate Communications (404) 878-3800 ATLANTA HAWKS PAY IT FORWARD AT LOCAL DUNKIN’ DONUTS RESTAURANTS Hawks “Paint the Town” at Two Locations; Team Pays for Orders and Serves Customers ATLANTA, GA ----- The Atlanta Hawks took over two Dunkin’ Donuts locations in Atlanta this morning and surprised customers by paying for their breakfast orders. Customers were greeted at the door with free team gear from Hawks players, cheerleaders and Harry the Hawk. The Atlanta Hawks activation team was also on-site giving away prizes and registering customers to win ticket packages to upcoming games. Beginning at 8:30 a.m., Hawks players Al Horford, Kyle Korver, Kent Bazemore, Dennis Schröder, Mike Muscala, Elton Brand, Pero Antic and Thabo Sefolosha interacted with customers at the Dunkin’ Donuts located at 1776 Howell Mill Road for an hour. At the same time, Paul Millsap, Jeff Teague, DeMarre Carroll, Mike Scott, John Jenkins, Adreian Payne and Shelvin Mack served customers at the 2420 Piedmont Ave, NE location. “Dunkin’ Donuts is very proud to be a partner with the Atlanta Hawks,” said Celia Cody, Field Marketing Manager, Dunkin’ Donuts. “This is our second season being a sponsor and we are so excited to have the players here this morning serving breakfast and delighting guests with great service.” Customers had their orders taken, delivered and paid for by the team. Dine-in and carryout customers took photos with the players and had their choice of a free Hawks cap, blanket, towel or foam hand sign. -

A Complete Breakdown of Every NBA Player's Salary, Where They
$1,422,720 (DonatasMotiejunas,Houston) $3,526,440 (JonasValanciunas,Toronto) Lithuania: $4,949,160 $12,350,000 (SergeIbaka,OklahomaCity) $3,049,920 (BismackBiyombo,Charlotte) Congo: $15,399,920 Total Salaries of Players that Schools Produced in Millions of US Dollars 100M 120M 140M 160M 180M 200M NBA Salary Distribution by Country that Produced Players SalaryDistributionbyCountrythatProduced NBA 20M 40M 60M 80M 947,907 (OmriCasspi,Houston) Israel: $947,907 0M 3 $10,105,855 |Gerald Wallace, Boston $3,250,000 |Alonzo Gee, Cleveland $2,652,000 |Mo Williams, Portland $3,135,000 |Jerryd Bayless, Boston Arizona $1,246,680 |Solomon Hill, Indiana $12,868,632 |Andre Iguodala, Golden State $3,500,000 |Jordan Hill, LA Lakers 10 $6,400,000 |Channing Frye Phoenix $5,625,313 |Jason Terry, Sacramento $5,016,960 |Derrick Williams, Sacramento $5,000,000 |Chase Budinger, Minnesota $226,162 |Mustafa Shaku, Oklahoma City $11,046,000 |Richard Jefferson, Utah Butler Bucknell Brigham Young Boston College Blinn College|$1.4M Belmont |$0.5M Baylor |$7.1M Arkansas-LR |$0.8M Arkansas |$23.1M Arizona State|$16M Arizona |$54M Alabama |$16M 3 $510,000 |Carrick Felix, Cleveland $13,701,250 |James Hardin, Houston $1,750,000 |Jeff Ayres, San Antonio 3 21,466,718 |Joe Johnson 884,293 |Jannero Pargo, Charlotte 1 788,872 |Patrick Beverey, Houston 884,293 |Derek Fisher, Oklahoma City A completebreakdownofeveryNBAplayer’ssalary,wheretheyplayedbeforetheNBA,andwhichschoolscountriesproducehighestnetsalary. 4 4,469,548 |Ekpe Udoh, Milwaukee 788,872 |Quincy Acy, Sacramento 788,872 -

Player - 2020-21 National Treasures Basketball
Set Info - Player - 2020-21 National Treasures Basketball Set Info - Player - 2020-21 National Treasures Basketball Player Total # Cards Total # Base Total # Autos Total # Memorabilia Total # Autos + Memorabilia Obi Toppin 1160 0 85 630 445 Deni Avdija 1155 0 80 630 445 Anthony Edwards 1147 0 72 630 445 James Wiseman 1147 0 72 630 445 Precious Achiuwa 1140 0 140 630 370 Devin Vassell 1140 0 140 630 370 Jordan Nwora 1140 0 140 630 370 Payton Pritchard 1140 0 140 630 370 LaMelo Ball 1136 0 61 630 445 Kira Lewis Jr 1130 0 140 630 360 Saddiq Bey 1129 0 140 630 359 RJ Hampton 1125 0 140 630 355 Jaden McDaniels 1119 0 140 630 349 Isaac Okoro 1101 0 101 630 370 Killian Hayes 1090 0 90 630 370 Tyrese Haliburton 1090 0 90 630 370 Patrick Williams 1090 0 90 630 370 Cole Anthony 1090 0 90 630 370 Onyeka Okongwu 1090 0 90 630 370 Immanuel Quickley 1065 0 140 630 295 Rudy Gobert 1015 167 0 848 0 Myles Turner 998 167 0 706 125 Malachi Flynn 994 0 90 630 274 Josh Green 989 0 0 630 359 Karl-Anthony Towns 979 167 126 565 121 CJ Elleby 964 0 0 630 334 Aleksej Pokusevski 945 0 22 628 295 Brandon Clarke 929 167 230 361 171 Udoka Azubuike 926 0 22 630 274 Jrue Holiday 870 167 230 302 171 LaMarcus Aldridge 869 167 206 250 246 Jarrett Culver 868 167 340 250 111 Bradley Beal 817 167 90 500 60 Jarrett Allen 718 0 0 608 110 Aaron Gordon 710 167 0 543 0 Hakeem Olajuwon 695 0 410 284 1 Bam Adebayo 693 167 56 470 0 Trae Young 693 167 132 326 68 Nikola Vucevic 693 167 0 451 75 Zion Williamson 693 167 61 403 62 Steven Adams 692 0 150 371 171 LeBron James 691 167 0