DOCSLIB.ORG

Development of an Equation of State for Gases Joseph J

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Development of an Equation of State for Gases Joseph J DEVELOPMENT OF AN EQUATION OF STATE FOR GASES JOSEPH J. MARTIN and YU-CHUN HOU University of Michigan, Ann Arbor, Michigan I. Pressure-Volume-Temperature Behavior of Pure Gases and Liquids 1 More than a hundred equations with any great degree of precision With any isotherm t,aken of state relating the pressure, vol- and not one of them is considered at ume, and temperature of gases suitable for the calculation of ac- Po= 0, 2, = 1.0, have been proposed according to curate thermodynamic diagrams. Dodge (7), but only a very few of This does not imply, however, that (dZ/dP,) = lim (2- 1)/ (P,- 0) them have attained any practical these two-constant equations have importance as the majority do not not been extremely useful. Van der as P, -+ 0 represent the data with sufficient Waals' equation was of the greatest accuracy. In this work the signifi- value in leading to the principle of = lim RT (Z - I)/RTP, cant pressure-volume-temperature corresponding states. as P, 0 (hereafter referred to as PVT) -+ In one form the corresponding- characteristics of pure gases have = (P,/RT)Iim(ZRT/P-RT/P) (5) been examined in detail, and an state principle suggests that the equation has been developed to fit compressibility factor, x = PVIRT, precisely the characteristics com- depends only on the reduced tem- mon to different gases. perature and pressure, which are PVT data may be plotted on dif- defined respectively as T, = TIT, ferent types of graphs, of which and P,= PIP,. On a generalized probably the oldest is that of pres- compressibility chart for many dif- sure vs. volume with temperature ferent compounds single average as a parameter, as shown in Fig- lines are drawn for each isotherm; ure 1. From this graph van der however, to demonstrate that the Waals deduced two properties of principle is approximate, Figure 2 the critical isotherm namely, that has been constructed to emphasize at the critical point the slope is the differences which actually exist zero and an inflection occurs.' Van among compounds. der Waals expressed these two From the compressibility chart properties algebraically in the fol- it is noted that all gases follow the lowing well-known manner : ideal-gas law as the pressure ap- proaches zero, regardless of the temperature. This may be expressed (dP/dVl~= 0 at the critical point as Z = PV/RT= 1at P = 0 for all (d2P/dV2),= 0 at the critical point FIG. 1. PRESSURE-VOLUMEDIAGRAM. temperatures (3) (2) ~ A curious corollary of where P is pressure, V is volume, this is the seemingly and T is temperature, as indicated contradictory fact that above. Van der Waals employed in general V does not these two conditions to evaluate equal RTIP at P=O. ---------- the two arbitrary constants in the By definition of a de- equation of state he proposed. rivative at any point A number of other two-constant (Po,2,) on the com- (exclusive of the gas constant) pressibility chart, equations of state have been pro- posed, the best known being those of Berthelot and Dieterici. None of them, however, actually represent (dZ/dPr)Tr the PVT data over a wide range -co*coyYD I - - COY.OW0 2 *Some investinations (13) indicate that the = lim (2 - Z,>/(p,- P,) critical isotherm- is not the smoothly inflected curve shown in Figure 1. This result seems to 0 Pr.10 be attributed to the indefiniteness of the -PI critical state and possibly to the lack of as P,-b P. attainment of true equilibrium. (4) FIG. 2. COMPRESSIBILITYCHART. Page 142 A.1.Ch.E. Journal June, 1955 Since by definition Z = PV/RT, or sumed indiscriminately either, or the essential inflection at the criti- ZRTIP = V,(dz/dP,)T, = cal point may not be preserved. In Figure 4 the necessary impli- (P,/RT) lim (V - R TIP)as P, --+ 0 cations of the assumption that the third derivative is zero are con- = - (Pc/BT)(cx)~,~-+O (6) sidered. In Figure 4d four possible curves have been drawn, all of where a is defined as the residual which go through zero according to volume, (RTIP-V). the assumption. If the true situa- If Equation (6) is rewritten, tion is similar to curve I, the fourth derivative must be positive, as at 0 pressure (Y shown in Figure 4e; the second derivative will pass through a = - (RT/PJ (dZ/’d’r)zr (7) minimum, as shown in Figure 4e; the first derivative will have an 0 aomula.Imwaswm which relates a to the slope of an To .I inflection, as shown in Figure 4b; isotherm on the compressibility FIG. 3. T, AS FUNCTIONOF T,. and the primary pressure vs. vol- chart. Since in general this slope ume curve will exhibit a minimum, is not zero at zero pressure, a is a as shown in Figure 4a. As the finite quantity. The one isotherm primary curve must show an in- for which the slope is zero is known flection, it is obvious that curve I as the Boyle point. cannot be correct. A similar analy- Most generalized compressibilty sis of curves I1 and 111, shows charts show the Boyle point occur- that they cannot be used; however, ring at a T, of about 2.5. This is curve 111, does give the required probably true only for such com- character of the pressure vs. vol- pounds as nitrogen, carbon mon- ume curve and therefore one con- oxide, and methane, which were cludes that if the third derivative considered in making the plots. is assumed to vanish, then the ‘These compounds all have critical fourth must also vanish, as shown temperatures of approximately the in Figure 4e, and the fifth must be same magnitude. For hydrogen negative or zero, as shown in Fig- with a much lower critical tempera- ure 4f. ture the data indicate that the Another assumption which can Boyle point is around a T, of 3.3. be made is that the fourth deriva- For compounds with higher critical tive vanishes while the third re- temperatures there are no experi- mains. An analysis similar to that mental data at the required high above shows that for this case the temperatures. However, by extra- third derivative must be negative polation of the experimental data in order to preserve the correct on isometric plots (see Figure 6), inflection at the critical point. The it appears that the Boyle-point re- hypothesis which is advanced here duced temperature goes down as is that in addition to the vanishing the critical temperature goes up FIG. 4. PRESSURE-VOLUMEDERIVATIVES of the first two derivatives, as sug- and that many compounds have gested by van der Waals, the third Boyle points much lower than a T= o AT CRITICAL derivative is either zero or a small T, of 2.5. Figure 3 is a plot of the a V3 negative number and the fourth Boyle point vs. critical tempera- POINT. [IT IS TAKENFOR GRANTED derivative is zero. Assumptions re- ture, prepared by consideration of garding the derivatives higher than ..AT(%), = 0, AND( a2p rI, o the measured points wherever pos- ) the fourth might be made, but sible and utilization of extrapola- a v2 these derivatives would have much tians to higher temperatures where AT CRITICAL POINT.] smaller effects. In current studies necessary, as just mentioned. the fifth and sixth derivatives are A characteristic’ of gas behavior being given some attention. noted on both the compressibility Another characteristic of gas be- chart and the pressure-volume plot havior noted on the compressibility is the straightness of the critical chart is that for compounds with .isotherm for a considerable range different values of 2, (PV/RT at 0n either side of the critical point. the critical point) lines which con- The length of the straight portion nect the critical point to the point indicates the possibility that deriva- Z= 1.0, P,=O are tangent to tives of pressure with respect to isotherms whose reduced tempera- volume higher than the two of van ture is about 0.8. Algebraically der Waals may be zero or at least this condition is very small. Examination of experi- mental data to prove whether any (dZ/dP,)T, = - (1 - 2,) derivatives higher than the second are zero is difficult, since the data at T’ Ei 0.8TC (8) are often not too accurate. The The meager data available indi- higher derivatives cannot be as- FIG.5. FIT, AS FUNCTIONOF 2,. cate that T’ varies slightly frorr! Vol. 1, No. 2 A.1.Ch.E. Journal Page 143 x - FIG.6. PRESSURE-TEMPERATURE DIAGRAM. would result in an error in its (d2P/dT2)v = 0 for high T (11) slope. From a thermodynamic point 0.8 according to the value of 2,. of view, the equality of the slope Figure 5 is a plot of the relation Also the isometrics below the of the vapor-pressure curve and between T and Z,, and it is seen critical density curve down, and the critical isometric has been that were it not for the low 2, of those above the critical density justified by the following analysis. water, it would be difficult to draw curve up.* These conditions are From the Clapeyron equation the any curve. Of course, there are given by the equations slope of the vapor-pressure curve other compounds with low Zc)s, but is dP/dT = ASIAV at any tempera- their data at a T,. of 0.8 are insuf- ture. At the critical point ASlAV ficient to warrant their use. becomes (dSldV)., but from the There are other characteristics Maxwell relation this is (dP/dT)Y,.
Load more

Recommended publications
  • How Compressible Are Innovation Processes?
    1 How Compressible are Innovation Processes? Hamid Ghourchian, Arash Amini, Senior Member, IEEE, and Amin Gohari, Senior Member, IEEE Abstract The sparsity and compressibility of finite-dimensional signals are of great interest in fields such as compressed sensing. The notion of compressibility is also extended to infinite sequences of i.i.d. or ergodic random variables based on the observed error in their nonlinear k-term approximation. In this work, we use the entropy measure to study the compressibility of continuous-domain innovation processes (alternatively known as white noise). Specifically, we define such a measure as the entropy limit of the doubly quantized (time and amplitude) process. This provides a tool to compare the compressibility of various innovation processes. It also allows us to identify an analogue of the concept of “entropy dimension” which was originally defined by R´enyi for random variables. Particular attention is given to stable and impulsive Poisson innovation processes. Here, our results recognize Poisson innovations as the more compressible ones with an entropy measure far below that of stable innovations. While this result departs from the previous knowledge regarding the compressibility of fat-tailed distributions, our entropy measure ranks stable innovations according to their tail decay. Index Terms Compressibility, entropy, impulsive Poisson process, stable innovation, white L´evy noise. I. INTRODUCTION The compressible signal models have been extensively used to represent or approximate various types of data such as audio, image and video signals. The concept of compressibility has been separately studied in information theory and signal processing societies. In information theory, this concept is usually studied via the well-known entropy measure and its variants.
    [Show full text]
  • Thermodynamics of Power Generation
    THERMAL MACHINES AND HEAT ENGINES Thermal machines ......................................................................................................................................... 1 The heat engine ......................................................................................................................................... 2 What it is ............................................................................................................................................... 2 What it is for ......................................................................................................................................... 2 Thermal aspects of heat engines ........................................................................................................... 3 Carnot cycle .............................................................................................................................................. 3 Gas power cycles ...................................................................................................................................... 4 Otto cycle .............................................................................................................................................. 5 Diesel cycle ........................................................................................................................................... 8 Brayton cycle .....................................................................................................................................
    [Show full text]
  • Chapter 3 3.4-2 the Compressibility Factor Equation of State
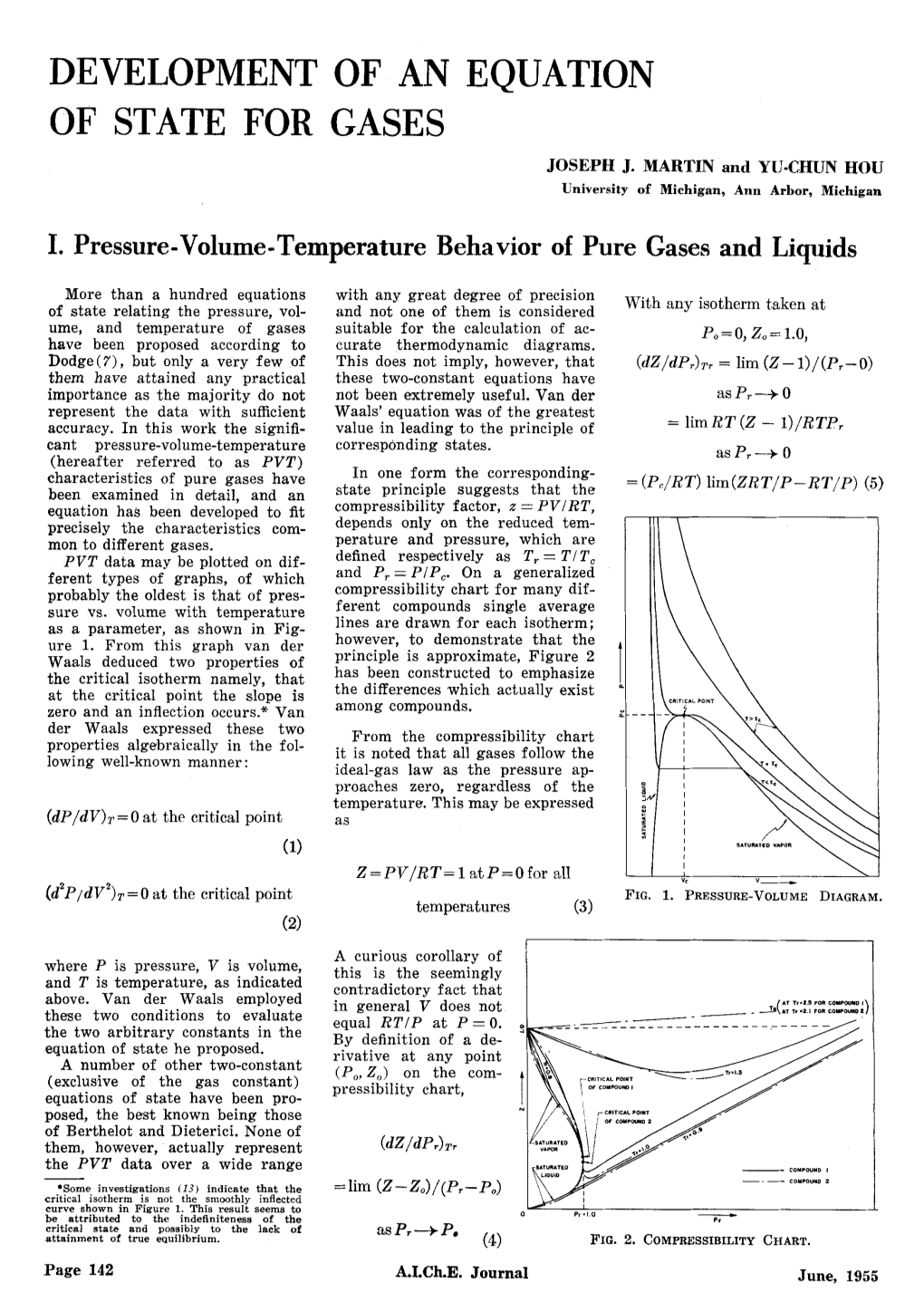
    Chapter 3 3.4-2 The Compressibility Factor Equation of State The dimensionless compressibility factor, Z, for a gaseous species is defined as the ratio pv Z = (3.4-1) RT If the gas behaves ideally Z = 1. The extent to which Z differs from 1 is a measure of the extent to which the gas is behaving nonideally. The compressibility can be determined from experimental data where Z is plotted versus a dimensionless reduced pressure pR and reduced temperature TR, defined as pR = p/pc and TR = T/Tc In these expressions, pc and Tc denote the critical pressure and temperature, respectively. A generalized compressibility chart of the form Z = f(pR, TR) is shown in Figure 3.4-1 for 10 different gases. The solid lines represent the best curves fitted to the data. Figure 3.4-1 Generalized compressibility chart for various gases10. It can be seen from Figure 3.4-1 that the value of Z tends to unity for all temperatures as pressure approach zero and Z also approaches unity for all pressure at very high temperature. If the p, v, and T data are available in table format or computer software then you should not use the generalized compressibility chart to evaluate p, v, and T since using Z is just another approximation to the real data. 10 Moran, M. J. and Shapiro H. N., Fundamentals of Engineering Thermodynamics, Wiley, 2008, pg. 112 3-19 Example 3.4-2 ---------------------------------------------------------------------------------- A closed, rigid tank filled with water vapor, initially at 20 MPa, 520oC, is cooled until its temperature reaches 400oC.
    [Show full text]
  • ESCI 241 – Meteorology Lesson 8 - Thermodynamic Diagrams Dr
    ESCI 241 – Meteorology Lesson 8 - Thermodynamic Diagrams Dr. DeCaria References: The Use of the Skew T, Log P Diagram in Analysis And Forecasting, AWS/TR-79/006, U.S. Air Force, Revised 1979 An Introduction to Theoretical Meteorology, Hess GENERAL Thermodynamic diagrams are used to display lines representing the major processes that air can undergo (adiabatic, isobaric, isothermal, pseudo- adiabatic). The simplest thermodynamic diagram would be to use pressure as the y-axis and temperature as the x-axis. The ideal thermodynamic diagram has three important properties The area enclosed by a cyclic process on the diagram is proportional to the work done in that process As many of the process lines as possible be straight (or nearly straight) A large angle (90 ideally) between adiabats and isotherms There are several different types of thermodynamic diagrams, all meeting the above criteria to a greater or lesser extent. They are the Stuve diagram, the emagram, the tephigram, and the skew-T/log p diagram The most commonly used diagram in the U.S. is the Skew-T/log p diagram. The Skew-T diagram is the diagram of choice among the National Weather Service and the military. The Stuve diagram is also sometimes used, though area on a Stuve diagram is not proportional to work. SKEW-T/LOG P DIAGRAM Uses natural log of pressure as the vertical coordinate Since pressure decreases exponentially with height, this means that the vertical coordinate roughly represents altitude. Isotherms, instead of being vertical, are slanted upward to the right. Adiabats are lines that are semi-straight, and slope upward to the left.
    [Show full text]
  • Steam Tables and Charts Page 4-1
    CHE 2012 Steam Tables and Charts Page 4-1 SECTION 4 STEAM TABLES AND CHARTS WATER AND STEAM Consider the heating of water at constant pressure. If various properties are to be measured, an experiment can be set up where water is heated in a vertical cylinder closed by a piston on which there is a weight. The weight acting down under gravity on a piston of fixed size ensures that the fluid in the cylinder is always subject to the same pressure. Initially the cylinder contains only water at ambient temperature. As this is heated the water changes into steam and certain characteristics may be noted. Initially the water at ambient temperature is subcooled. As heat is added its temperature rises steadily until it reaches the saturation temperature corresponding with the pressure in the cylinder. The volume of the water hardly changes during this process. At this point the water is saturated. As more heat is added, steam is generated and the volume increases dramatically since the steam occupies a greater space than the water from which it was generated. The temperature however remains the same until all the water has been converted into steam. At this point the steam is saturated. As additional heat is added, the temperature of the steam increases but at a faster rate than when the water only was being heated. The Page 4-2 Steam Tables and Charts CHE 2012 volume of the steam also increases. Steam at temperatures above the saturation temperature is superheated. If the temperature T is plotted against the heat added q the three regions namely subcooled water, saturated mixture and superheated steam are clearly indicated.
    [Show full text]
  • A Thermodynamic Theory of Economics
    ________________________________________________________________________________________________ A Thermodynamic Theory of Economics Final Post Review Version ________________________________________________________________________________________________ John Bryant VOCAT International Ltd, 10 Falconers Field, Harpenden, AL5 3ES, United Kingdom. E-mail: [email protected] Abstract: An analogy between thermodynamic and economic theories and processes is developed further, following a previous paper published by the author in 1982. Economic equivalents are set out concerning the ideal gas equation, the gas constant, pressure, temperature, entropy, work done, specific heat and the 1st and 2nd Laws of Thermodynamics. The law of diminishing marginal utility was derived from thermodynamic first principles. Conditions are set out concerning the relationship of economic processes to entropic gain. A link between the Le Chatelier principle and economic processes is developed, culminating in a derivation of an equation similar in format to that of Cobb Douglas production function, but with an equilibrium constant and a disequilibrium function added to it. A trade cycle is constructed, utilising thermodynamic processes, and equations are derived for cycle efficiency, growth and entropy gain. A thermodynamic model of a money system is set out, and an attempt is made to relate interest rates, the rate of return, money demand and the velocity of circulation to entropy gain. Aspects concerning the measurement of economic value in thermodynamic terms are discussed. Keywords: Thermodynamics, economics, Le Chatelier, entropy, utility, money, equilibrium, value, energy. Publisher/Journal: This paper is the final post review version of a paper submitted to the International Journal of Exergy, published by Inderscience Publishers. Reference: Bryant, J. (2007) ‘A thermodynamic theory of economics’, Int. J. Exergy, Vol 4, No.
    [Show full text]
  • Real Gases – As Opposed to a Perfect Or Ideal Gas – Exhibit Properties That Cannot Be Explained Entirely Using the Ideal Gas Law
    Basic principle II Second class Dr. Arkan Jasim Hadi 1. Real gas Real gases – as opposed to a perfect or ideal gas – exhibit properties that cannot be explained entirely using the ideal gas law. To understand the behavior of real gases, the following must be taken into account: compressibility effects; variable specific heat capacity; van der Waals forces; non-equilibrium thermodynamic effects; Issues with molecular dissociation and elementary reactions with variable composition. Critical state and Reduced conditions Critical point: The point at highest temp. (Tc) and Pressure (Pc) at which a pure chemical species can exist in vapour/liquid equilibrium. The point critical is the point at which the liquid and vapour phases are not distinguishable; because of the liquid and vapour having same properties. Reduced properties of a fluid are a set of state variables normalized by the fluid's state properties at its critical point. These dimensionless thermodynamic coordinates, taken together with a substance's compressibility factor, provide the basis for the simplest form of the theorem of corresponding states The reduced pressure is defined as its actual pressure divided by its critical pressure : The reduced temperature of a fluid is its actual temperature, divided by its critical temperature: The reduced specific volume ") of a fluid is computed from the ideal gas law at the substance's critical pressure and temperature: This property is useful when the specific volume and either temperature or pressure are known, in which case the missing third property can be computed directly. 1 Basic principle II Second class Dr. Arkan Jasim Hadi In Kay's method, pseudocritical values for mixtures of gases are calculated on the assumption that each component in the mixture contributes to the pseudocritical value in the same proportion as the mol fraction of that component in the gas.
    [Show full text]
  • Thermodynamics As a Substantive and Formal Theory for the Analysis of Economic and Biological Systems
    Thermodynamics as a Substantive and Formal Theory for the Analysis of Economic and Biological Systems The research presented in this thesis was carried out at the Department of Theoretical Life Sciences, Vrije Universiteit Amsterdam, The Netherlands and at the Environment and Energy Section, Instituto Superior T´ecnico, Lisbon, Portugal. VRIJE UNIVERSITEIT THERMODYNAMICS AS A SUBSTANTIVE AND FORMAL THEORY FOR THE ANALYSIS OF ECONOMIC AND BIOLOGICAL SYSTEMS ACADEMISCH PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Vrije Universiteit Amsterdam, op gezag van de rector magnificus prof.dr. L.M. Bouter, in het openbaar te verdedigen ten overstaan van de promotiecommissie van de faculteit der Aard- en Levenswetenschappen op dinsdag 6 februari 2007 om 10.00 uur in de aula van de Instituto Superior T´ecnico Av. Rovisco Pais, n◦1 1049-001 Lisboa door Taniaˆ Alexandra dos Santos Costa e Sousa geboren te Beira, Mozambique promotor: prof.dr. S.A.L.M. Kooijman Contents 1 Introduction 1 2 IsNeoclassicalEconomicsFormallyValid? 9 Published in Ecological Economics 58 (2006): 160-169 2.1 Introduction................................. 10 2.2 IstheFormalismofNeoclassicalEconomicswrong? . ...... 12 2.3 A Unified Formalism for Neoclassical Economics and Equilibrium Ther- modynamics................................. 14 2.4 DiscussingtheFormalism. 19 2.5 Conclusions................................. 21 3 Equilibrium Econophysics 29 Published in Physica A 371 (2006): 492-512 3.1 Introduction................................. 30 3.2 FundamentalEquationandtheEquilibriumState . ...... 31 3.3 DualityFormulation............................. 33 3.4 Reversible, Irreversible and Impossible Processes . .......... 35 3.5 Many-stepProcesses ............................ 36 3.6 LegendreTransforms ............................ 38 3.7 Elasticities.................................. 40 3.8 MaxwellRelations ............................. 43 3.9 StabilityConditions and the Le Chatelier Principle . ......... 45 3.10 EquationsofStateandIntegrability . ..... 47 3.11 FirstOrderPhaseTransitions .
    [Show full text]
  • Analysis of Thermodynamic Processes with Full Consideration of Real Gas Behaviour
    Analysis of thermodynamic processes with full consideration of real gas behaviour Version 2.12. - (July 2020) engineering your visions © by B&B-AGEMA, No. 1 Contents • What is TDT ? • How does it look like ? • How does it work ? • Examples engineering your visions © by B&B-AGEMA, No. 2 Introduction What is TDT ? TDT is a Thermodynamic Design Tool, that supports the design and calculation of energetic processes on a 1D thermodynamic approach. The software TDT can be run on Windows operating systems (Windows 7 and higher) or on different LINUX-platforms. engineering your visions © by B&B-AGEMA, No. 3 TDT - Features TDT - Features 1. High calculation accuracy: • real gas properties are considered on thermodynamic calculations • change of state in each component is divided into 100 steps 2. Superior user interface: • ease of input: dialogs on graphic screen • visualized output: graphic system overview, thermodynamic graphs, digital data in tables 3. Applicable various kinds of fluids: • liquid, gas, steam (incl. superheated, super critical point), two-phase state • currently 29 different fluids • user defined fluid mixtures engineering your visions © by B&B-AGEMA, No. 4 How does TDT look like ? engineering your visions © by B&B-AGEMA, No. 5 TDT - User Interface Initial window after program start: start a “New project”, “Open” an existing project, open one of the “Examples”, which are part of the installation, or open the “Manual”. engineering your visions © by B&B-AGEMA, No. 6 TDT - Main Window Structure tree structure action toolbar notebook containing overview and graphs calculation output On the left hand side of the window the entire project information is listed in a tree structure.
    [Show full text]
  • Compressibility of the Fluid
    EPJ Web of Conferences 67, 02048 (2014) DOI: 10.1051/epjconf/20146702048 C Owned by the authors, published by EDP Sciences, 2014 Compressibility of the fluid Jana Jablonská1,a 1 Department of Hydromechanics and Hydraulic Equipment, Faculty of Mechanical Engineering, VŠB-Technical University of Ostrava, 17. listopadu 15, 708 33 Ostrava, Czech republic Abstract. The presence of air in the liquid causes the dynamic system behaviour. When solve to issue of the dynamics we often meet problems of cavitation. Cavitation is an undesirable phenomenon, since it causes a disruption of the surrounding material and material destruction. Cavitation is accompanied by loud sound effects and reduces the efficiency of such pumps, etc. Therefore, it is desirable to model systems in which the cavitation might occur. A typical example is a solution of water hammer. 1 Introduction Fluid density after compression is given by m m In solving dynamics of hydraulic systems we often 0 4 4 (4) encounter the problem with cavitation. Cavitation is an V0 V 1 p 1 p undesirable phenomenon that we are trying to prevent. Cavitation depends on the liquid used in the hydraulic Thereof system. Liquids - hydraulic fluids are typical of its air content. The air in the fluid occurs in two forms - C p S D1 T (5) dissolved and undissolved. Dissolved air according to the 0 E K U literature [4] ia controled by Henry's law, its release is complex and difficult to describe action. If we consider the fluid flow with undissolved air it is a flow of mixture - water – air. 3 Determining the modulus of elasticity of liquid 2 Compressibility of the fluid The modulus of elasticity of water is generally in the literature determines the value of 2.1·109 Pa under normal Compressibility of the fluid is character to shrink in conditions, which corresponds to theory 1 (see Figure 3).
    [Show full text]
  • Thermodynamic/Aerological Charts/Diagrams
    THERMODYNAMIC/AEROLOGICAL CHARTS/DIAGRAMS 1 /31 • Thermodynamic charts are used to represent the vertical structure of the atmosphere, as well as major thermodynamic processes to which moist air can be subjected. • Thermodynamic charts can be used to obtain easily different thermodynamic properties, e.g. q (potential temperature) and moisture quantities (such as the specific humidity), from a given radiosonde ascent. • Even though today it is possible to compute many quantities directly, thermodynamic diagrams are still very useful and remain videly used. 2 /31 • Each diagram has lines of constant: – p, pressure, – T, temperature, – q, potential temperature, – q, saturation specific humidity. – saturated adiabats. • One difficulty of all diagrams is that they are two dimensional, and the most compact description of the state of the atmosphere encompasses three dimensions, for instance, {T,p,q}. 3 /31 • The simplest and most common form of the aerological diagram has pressure as the ordinate and temperature as the abscissa – the temperature scale is linear – it is usually desirable to have the ordinate approximately representative of height above the surface, thus The ordinate may be proportional to –ln p (the Emagram) or to pR/cp (the Stuve diagram). • The Emagram has the advantage over the Stuve diagram in that area on the diagram is proportional to energy: dw = pdυ = RdT −υdp dp dw = R dT − RT RdT is an exact differential which integrates to zero !∫ !∫ !∫ p !∫ dw = −R!∫ Td(ln p) • A chart with coordinates of T versus ln p has the property of a true thermodynamic diagram, i.e. the area is proportional to energy.
    [Show full text]
  • Adiabatic Processes and Thermodynamic Diagrams
    ATSC 5010 – Physical Meteorology I Lab Lab 3 – Adiabatic Processes & Thermodynamic Diagrams è Begin with the first law of thermodynamics: �� = �� − �� (1) where: dq is heat input to a gas du is the increase in internal energy dw is the work done by the gas; in atmosphere—only concerned with work due to expansion, thus dw=pdv: �� = �� − ��� (2) Equation (2) is true for a reversible process in a P-V-T system. In class, we also defined enthalpy: h=u+pv to derive the enthalpy form of the first law: �ℎ = �� + ��� (3) We define the specific heat constant as the change in heat with respect to temperature (δq/δT) and at constant pressure this is equal to cp. Thus, we can rewrite equation (3) as: �!�� = �� + ��� (4) è For an adiabatic process, no heat is added or lost from the system: �� = 0 , and eqn (4) becomes: �!�� = ���, which can be simplified considering a reversible process for a P-V-T system: �� � �� = �� (5) ! � Integrating eqn (5) from initial state (T0, P0) to final state (T,P) leads to one of the 3 Poisson relationships: ! ! ! �� �� � � !! � = � → = ! � ! � � � !! !! ! ! 5 è For P0 equal to 10 Pa (1000 mb), then we define the Potential Temperature, θ, as T0. Further, if we only consider dry air, then we can use the dry air gas constant and specific heat at constant volume: !! 10! !!" � = � � Exercises: Today you will construct a thermodynamic diagram called an emagram. An emagram can be used to determine the relationship between temperature, pressure, and potential temperature. You will use your emagram to answer questions about how a parcel’s state changes as it undergoes different processes.
    [Show full text]