DOCSLIB.ORG

Optomechanical Crystals in Cavity Opto- and Electromechanics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optomechanical Crystals in Cavity Opto- and Electromechanics Optomechanical Crystals in Cavity Opto- and Electromechanics Johannes Fink and Oskar Painter Institute for Quantum Information and Matter California Institute of Technology Announcements 2016: New Institute, brand new lab à Quantum integrated devices Deadline: Feb 7, 2016 (quantumids.com) - Circuit QED - Electro- and Optomechanics - Integrated microwave to optical link - Quantum communication & imaging Cavity Optomechanics Physics Hint = ~gomxaˆ †a = ~g0(b + b†)a†a xˆ = xzpf(b + b†) Aspelmeyer, Kippenberg, Marquardt Rev. Mod. Phys. 86 (2014) Why Mechanics? • Fundamental tests • Mechanics as a bus gravitation, decoherence connecting qubits, spins, photons, atoms, ... • Precision measurements displacements, masses, forces, • Mechanics as a toolbox accelerations storage, amplification, filtering, multiplexing, sensing, … • Mechanical circuits and arrays nonlinearities for QIP, collective dynamics Optomechanical Crystals Periodic Atomic Structure 0.5 nm àBandgaps for fo = 194 THz electron waves Periodically Placed Holes fm = 5.7 GHz à Bandgaps for sound & 500 nm light waves • Independent routing of acoustic and optical waves • Strong co-localization of modes • Large radiation pressure effect (g0) Coupling Strength • Phononic shield for high mechanical Q • Telecom wavelengths go = 1,100 kHz (experiment) • <n> << 1 at 10 mK J. Chan, et. al, Nature 478 (2011) Outline Lectures 1-3: Basics of OMCs Design & Engineering OMCs & Microwaves 1. Maxwell’s equations 1. OMC Band structures 1. Slot mode coupled PCs a) Basics a) Design b) Energy, mode 2. Linear and point defects b) Coupling volume and a) Basics c) Nonlinearities quantization b) 1D Nanobeam c) Symmetry and c) W1 Snowflake 2. Slot mode coupled ‘OMCs’ periodicity a) Design & coupling d) Band structures 3. OM Coupling b) Fabrication a) Boundary c) EIT 2. Acoustic wave equation b) Stress-Optical d) Ground state a) Basics c) Vacuum coupling e) TLS coupling b) Effective mass f) Wavelength c) Guided waves 4. Techniques conversion d) Band structures a) Fabrication b) Coupling 3. Outlook Optomechanical Crystals in Cavity Opto- and Electromechanics Basics of OMCs Maxwell’s Equations I Most general Linear and lossless Mixed dielectric medium Solutions are harmonic modes - No sources of light: With e.g. - Linear: - Isotropic Implications - No material dispersion - Lossless: is real and pos. - transversality - = 1 - “Master equation” à J. D. Joannopoulos, et. al, Princeton University Press (2008) Maxwell’s Equations II Procedure Eigenvalue Problem - For a given ε(r) - We can define operator Θ - Θ is linear and hermitian -> ω is real, modes are orthogonal 1D Example - Solve - Inner product - orthogonal modes to find mode profile Normalization - Then use e.g. - with - and to recover electric field profile (and make sure \ ) J. D. Joannopoulos, et. al, Princeton University Press (2008) Energy, Mode Volume, Quantization Variational Principle Quantization - Minimize EM energy functional -> minimize Uf to get lowest energy mode 2 2 ω0 /c subject to Physical Energy - For harmonic mode, time averaged ß max by definition Effective Mode Volume Relation to cavity / circuit QED - Depends on physics - Dipole moment - Electric field - Dipole coupling - Minimal possible in dielectric cavity ~ with ZPF (1D): with 2 - About ~ 0.01 μm3 (Si at 1550 nm) V usually normalized with |E(ratom)| J. D. Joannopoulos, et. al, Princeton University Press (2008) M. O. Scully, et. al, Cambridge University Press (1997) Symmetry and Bloch Waves Inversion Symmetry Continuous Translational Symmetry - Even odd - Operator - Solution (1D) - Homogeneous medium (3D): ε=1 -> plane waves -> disp. relation - Symmetry operator: Plane of glass - is also a valid mode with - Free space Band structure and α = 1 or -1 - Symmetry operations can be used to - Light line classify modes (without knowing the details of it) - Index guided J. D. Joannopoulos, et. al, Princeton University Press (2008) Periodicity and Bands Discrete Translational Symmetry Bloch Theorem (3D) - Bloch state vector - Reciprocal lattice vectors - Plane waves again Photonic Bands - Degenerate set - Operator - Reciprocal lattice vector - Transversality - Bloch - Periodicity - Brillouin zone à use MPB to get for a given J. D. Joannopoulos, et. al, Princeton University Press (2008) IBZ and Propagation Irreducible Brillouin Zone Polarization - e.g. Rotational symmetry: - 2D photonic crystals have symmetry - Allows only two different polarizations à Symmetries of the lattice are inherited by the bands TE: à Additional redundancy in the BZ TM: - In general: Bands have symmetries of point group (Rotation, Reflection, Inversion) Bloch wave propagation - IBZ of square Lattice - With time dependence à k is conserved à All scattering events are coherent - Group velocity J. D. Joannopoulos, et. al, Princeton University Press (2008) Photonic Band Gaps 1D Photonic Crystal Band structure - A multilayer film - Bloch state ε=(13,13) ε=(13,12) ε=(13,1) - BZ is 1D - PBG forms at where λ = 2 a - Consider only kz dielectric band air band - Layer width a/2 - Light line - Bandgap scales with Δε J. D. Joannopoulos, et. al, Princeton University Press (2008) Photonic Band Gaps 2D Photonic Crystal Band structure - A set of rods - k z = 0, r = 0.2 a, ε= (8.9, 1) - Band gap in x-y plane - Can prevent light to propagate in any direction in this plane - Modes in x-y plane are TE: H normal to plane or - TM modes: TM: normal to plane E - Zero group velocity (standing waves) at X and M - Bloch state - Only TM has band gap à “symmetry BG” J. D. Joannopoulos, et. al, Princeton University Press (2008) Band Gaps & Slabs Triangular Lattice: Complete BG Triangular Lattice in a Slab - Compromise: weakly connected “rods” - Index guiding in z direction - Forms “quasi” photonic band gap (only for guided modes below light cone) - Band modes decay as exp( i (k + i κ) z) - Avoid leakage: - Hexagonal BZ, BG for all polarizations - Out of plane radiation - TM –TE mixing - But no confinement to x-y plane J. D. Joannopoulos, et. al, Princeton University Press (2008) Acoustic Wave Equation Continuum mechanics Eigenvalue Problem λ ( p >> interatomic distances) - Material properties: - with operator elasticity tensor density displacement vector field Quantization again - Strain (relative deformation) - Define ladder operators for each mode - Stress (Hooke’s law) - Single phonon energy - Newton’s law - With ZPF - Wave eqn. - And A. H. Safavi-Naeini and O. Painter, Springer (2014) Waves and Phonons 1 Guided waves Phonons in a slab - EM modes 2 transverse waves (different pol.) with: - Mechanical modes 2 transverse (shear) waves with 1 longitudinal (dilatational, pressure) wave with - Propagation - Polarization (SH), (SV) and (P) - Mirror symmetry: (-x+z), (+x-z), (+x+z) Material operator e.g. - Boundary: - Typical properties of SOI (Si) - Horizontal shear (SH) dispersion - Slab boundary couples SV and P modes - Form pair of solutions: λ = 1500 nm (-z) … flexural and (+z) … extensional T = 220 nm - Level repulsion causes low energy dispersion difference A. H. Safavi-Naeini and O. Painter, Springer (2014) Waves and Phonons 2 Phonons in a beam - Additional boundary condition - Boundaries also couples SH modes - 2 flexural modes and one extensional (+x+z) - One additional torsional mode (-x-z) A. H. Safavi-Naeini and O. Painter, Springer (2014) Phononic Band Structures 1D chain with basis 1D pad connector - Symmetries - Dispersion relation - Acoustic is linear at small k - Band gap scales with Δm (and K) - For N > 2 masses: acoustic: 2 + 1 optical: 3 N - 3 - à phononic bandgap modes M. Eichenfield, et. Al. Optics Express 17 (2009) A. H. Safavi-Naeini and O. Painter, Optics Express 18 (2010) Optomechanical Crystals in Cavity Opto- and Electromechanics Design and Engineering OMC Band Structures 1 Quasi - 1D Nanobeam crystal Lattice: photonic bands: phononic bands: - Symmetry points: Γ(k=0), M (k=π/a) - Optics: Fundametal TE modes in black - Mechanics: Extensional modes shown in black A. H. Safavi-Naeini and O. Painter, Optics Express 18 (2010) OMC Band Structures 2 Quasi 2D Cross crystal Lattice: photonic bands: phononic bands: (even, vertical sym.) à Bad choice for OMC à Great choice for phononic shield A. H. Safavi-Naeini and O. Painter, Springer (2014) OMC Band Structures 3 Quasi 2D Snowflake crystal Lattice: photonic bands: phononic bands: (even, vertical sym.) à Higher symmetry à Independent tuning a-2r (phononics) and w (photonics) à Great choice for OMC A. H. Safavi-Naeini and O. Painter, Springer (2014) Point defects 1 Point defect in 1D Localization - Defect modes decay exponentially in crystal - Defect in multilayer film - Evanescent with complex k+iκ - Can approximate - Density of states - Large k and small V at midgap - Defect allows localized mode - νspecific “mirrors” for cavity - Can “pull” or “push” a defect from any band - Strong confinement causes radiation loss J. D. Joannopoulos, et. al, Princeton University Press (2008) Point defects 2 1D Nanobeam cavity photonic phononic mech. and opt. cavity mode defect - Push optical defect for X point ß further from light cone - Pull mechanical defect from Γ point ß constructive overlap with optical mode - Choose a quadratic scaling of the defect ß minimize wave package in real and reciprocal space 2 - Numerical optimization of geometry with fitness function, e.g. g0 /κ A. H. Safavi-Naeini and O. Painter, Optics Express 18 (2010) Linear defects Example: Waveguide in air - Introduce line defect in 2D crystal - One direction with discrete translational symmetry - ky in propagation
Load more

Recommended publications
  • Controlling Phonons and Photons at the Wavelength-Scale: Silicon Photonics Meets Silicon Phononics
    1 Controlling phonons and photons at the wavelength-scale: silicon photonics meets silicon phononics AMIR H. SAFAVI-NAEINI1,D RIES VAN THOURHOUT2,R OEL BAETS2, AND RAPHAËL VAN LAER1,2 1Department of Applied Physics and Ginzton Laboratory, Stanford University, USA 2Photonics Research Group (INTEC), Department of Information Technology, Ghent University–imec, Belgium .Center for Nano- and Biophotonics, Ghent University, Belgium Compiled October 9, 2018 Radio-frequency communication systems have long used bulk- and surface-acoustic-wave de- vices supporting ultrasonic mechanical waves to manipulate and sense signals. These devices have greatly improved our ability to process microwaves by interfacing them to orders-of- magnitude slower and lower loss mechanical fields. In parallel, long-distance communications have been dominated by low-loss infrared optical photons. As electrical signal processing and transmission approaches physical limits imposed by energy dissipation, optical links are now being actively considered for mobile and cloud technologies. Thus there is a strong driver for wavelength-scale mechanical wave or “phononic” circuitry fabricated by scalable semiconduc- tor processes. With the advent of these circuits, new micro- and nanostructures that combine electrical, optical and mechanical elements have emerged. In these devices, such as optomechan- ical waveguides and resonators, optical photons and gigahertz phonons are ideally matched to one another as both have wavelengths on the order of micrometers. The development of phononic circuits has thus emerged as a vibrant field of research pursued for optical signal pro- cessing and sensing applications as well as emerging quantum technologies. In this review, we discuss the key physics and figures of merit underpinning this field.
    [Show full text]
  • Electrical Engineering Engineering
    College of Electrical Engineering Engineering The undergraduate electrical engineering degree program seeks to produce gradu- Second Semester ates who are trained in the theory and practice of electrical and computer engineering EE 468G Introduction to Engineering Electromagnetics ........................................ 4 and are well prepared to handle the professional and leadership challenges of their Elective EE Laboratory [L] ...................................................................................... 2 careers. The program allows students to specialize in high performance and embed- Engineering/Science Elective [E] ............................................................................ 3 ded computing, microelectronics and nanotechnology, power and energy, signal Technical Elective [T] ............................................................................................. 3 processing and communications, high frequency circuits and fields, and control UK Core – Citizenship - USA .................................................................................. 3 systems, among others. Senior Year Degree Requirements The following curriculum meets the requirements for a B.S. in Electrical Engineering, First Semester Hours provided the student satisfies UK Core requirements and graduation requirements EE/CPE 490 ECE Capstone Design I† ..................................................................... 3 of the College of Engineering. EE Technical Elective* ...........................................................................................
    [Show full text]
  • Methods of Using Mobile Internet Devices in the Formation of The
    217 Methods of using mobile Internet devices in the formation of the general scientific component of bachelor in electromechanics competency in modeling of technical objects Yevhenii O. Modlo1[0000-0003-2037-1557], Serhiy O. Semerikov2,3,4[0000-0003-0789-0272], Stanislav L. Bondarevskyi3[0000-0003-3493-0639], Stanislav T. Tolmachev3[0000-0002-5513-9099], Oksana M. Markova3[0000-0002-5236-6640] and Pavlo P. Nechypurenko2[0000-0001-5397-6523] 1 Kryvyi Rih Metallurgical Institute of the National Metallurgical Academy of Ukraine, 5, Stephana Tilhy Str., Kryvyi Rih, 50006, Ukraine [email protected] 2 Kryvyi Rih State Pedagogical University, 54, Gagarina Ave., Kryvyi Rih, 50086, Ukraine [email protected], [email protected] 3 Kryvyi Rih National University, 11, Vitaliy Matusevych Str., Kryvyi Rih, 50027, Ukraine [email protected], [email protected], [email protected] 3 Institute of Information Technologies and Learning Tools of NAES of Ukraine, 9, M. Berlynskoho Str., Kyiv, 04060, Ukraine Abstract. An analysis of the experience of professional training bachelors of electromechanics in Ukraine and abroad made it possible to determine that one of the leading trends in its modernization is the synergistic integration of various engineering branches (mechanical, electrical, electronic engineering and automation) in mechatronics for the purpose of design, manufacture, operation and maintenance electromechanical equipment. Teaching mechatronics provides for the meaningful integration of various disciplines of professional and practical training bachelors of electromechanics based on the concept of modeling and technological integration of various organizational forms and teaching methods based on the concept of mobility. Within this approach, the leading learning tools of bachelors of electromechanics are mobile Internet devices (MID) – a multimedia mobile devices that provide wireless access to information and communication Internet services for collecting, organizing, storing, processing, transmitting, presenting all kinds of messages and data.
    [Show full text]
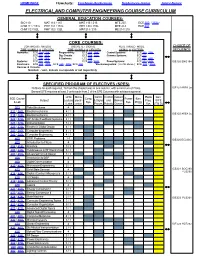
  • Electrical and Computer Engineering Course
    HOMEPAGE Flowcharts: Freshman-Sophomore Sophomore-Junior Junior-Senior ELECTRICAL AND COMPUTER ENGINEERING COURSE CURRICULUM GENERAL EDUCATION COURSES: BIO 110 MAT 114 / 115 MAT 116 / 216 MTE 207 ECE 302 / 352L* CHM 111 / 151L PHY 131 / 151L PHY 133 / 153L MTE 214 ECE 311 CHM 112 / 152L PHY 132 / 132L MAT 214 / 215 ME 214 / 215 CORE COURSES: CONTINOUS / ANALOG DISCRETE / DIGITAL REAL / MIXED MODE CHOICE OF TIME SIGNALS & CIRCUITS TIME SIGNALS & CIRCUITS SIGNAL & SYSTEMS SEQUENCE Networks: ECE 109 / 129L Programming: ECE 114 , 164L Control Systems: ECE 309 , 359L ECE 207 , 252L Dig. Circuits ECE 204 , 244L Commu. Systems: ECE 315 ECE 209 , 253L & Systems: ECE 308 ECE 405 , 445L Systems: ECE 307 , 357L ECE 341 / 391L Power Systems: ECE 310 / 360L IGE120 ENG104 Electronic ECE 220 , 270L , ECE 320 , 370L, ECE 330 *Electromagnetics: ( in GE above ) ECE 302 / 352L Devices & Circuits: Notation: / and , indicate co-requisiste or not respectively SPECIFIED PROGRAM OF ELECTIVES (SPES) 20 Units for each required, 16 from the shaded ares in one column, with a minimum of 2 labs. IGE121AREA 3a General SPE requires at least 5 units each from 2 of the SPE Columns with advisors approval. Units Micro- Comm. Control Instrum Radio Gen. ECE Course Comp. Power Illum. Subject Lecture electr- & Signal and Biomed Freq. S P E & Lab Sys. Sys. Engg / Labs onics Proces. Robotic Ocean Sys. (T B D) 303 Data Structures 4 317 / 367L Electromechanics 4 / 1 IGE122 AREA 3c 318 / 368L Electromechanics 4 / 1 322 / 372L OP Amps./Feedback Systems 4 / 1 323 / 373L Instrumentation
    [Show full text]
  • Electromechanical Motion Fundamentals
    Electromechanical Motion Fundamentals • Electric Machine – device that can convert either mechanical energy to electrical energy or electrical energy to mechanical energy – mechanical to electrical: generator – electrical to mechanical: motor – all practical motors and generators convert energy from one form to another through the action of a magnetic field • Transformer – device that converts ac electric energy at one voltage level to ac electric energy at another voltage level Sensors & Actuators in Mechatronics K. Craig Electromechanical Motion Fundamentals 1 – It operates on the same principles as generators and motors, i.e., it depends on the action of a magnetic field to accomplish the change in voltage level • Motors, Generators, and Transformers are ubiquitous in modern daily life. Why? – Electric power is: • Clean • Efficient • Easy to transmit over long distances • Easy to control • Environmental benefits Sensors & Actuators in Mechatronics K. Craig Electromechanical Motion Fundamentals 2 • Purpose of this Study – provide basic knowledge of electromechanical motion devices for mechatronic engineers – focus on electromechanical rotational devices commonly used in low-power mechatronic systems • permanent magnet dc motor • brushless dc motor • stepper motor • Topics Covered: – Magnetic and Magnetically-Coupled Circuits – Principles of Electromechanical Energy Conversion Sensors & Actuators in Mechatronics K. Craig Electromechanical Motion Fundamentals 3 References • Electromechanical Motion Devices, P. Krause and O. Wasynczuk, McGraw Hill, 1989. • Electromechanical Dynamics, H. Woodson and J. Melcher, Wiley, 1968. • Electric Machinery Fundamentals, 3rd Edition, S. Chapman, McGraw Hill, 1999. • Driving Force, The Natural Magic of Magnets, J. Livingston, Harvard University Press, 1996. • Applied Electromagnetics, M. Plonus, McGraw Hill, 1978. • Electromechanics and Electric Machines, S. Nasar and L. Unnewehr, Wiley, 1979.
    [Show full text]
  • Electromechanical Dynamics
    Electromechanical Dynamics James R. Melcher Herbert H. Woodson MIT OpenCourseWare http://ocw.mit.edu Electromechanical Dynamics For any use or distribution of this textbook, please cite as follows: Woodson, Herbert H., and James R. Melcher. Electromechanical Dynamics. 3 vols. (Massachusetts Institute of Technology: MIT OpenCourseWare). http://ocw.mit.edu (accessed MM DD, YYYY). License: Creative Commons Attribution-NonCommercial-Share Alike For more information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms ELECTROMECHANICAL DYNAMICS Part I: Discrete Systems ELECTROMECHANICAL DYNAMICS Part I: Discrete Systems HERBERT H. WOODSON Philip Sporn Professor of Energy Processing Departments of Electrical and Mechanical Engineering JAMES R. MELCHER Associate Professor of Electrical Engineering Department of Electrical Engineering both of Massachusetts Institute of Technology JOHN WILEY & SONS, INC., NEW YORK - LONDON . SYDNEY __ ~__ To our parents I_ PREFACE Part I: Discrete Systems In the early 1950's the option structure was abandoned and a common core curriculum was instituted for all electrical engineering students at M.I.T. The objective of the core curriculum was then, and is now, to provide a foundation in mathematics and science on which a student can build in his professional growth, regardless of the many opportunities in electrical engineering from which he may choose. In meeting this objective, core curriculum subjects cannot serve the needs of any professional area with respect to nomenclature, techniques, and problems unique to that area. Specialization comes in elective subjects, graduate study, and professional activities. To be effective a core curriculum subject must be broad enough to be germane to the many directions an electrical engineer may go professionally, yet it must have adequate depth to be of lasting value.
    [Show full text]
  • Campus Curricula Committee Meeting Agenda April 3, 2013 12 Pm Room 117 Fulton Hall
    Campus Curricula Committee Meeting Agenda April 3, 2013 12 pm Room 117 Fulton Hall Review of submitted DC forms: DC #0454, Electrical and Computer Engineering, Bachelor of Science in Electrical Engineering, effective Fall 2013. DC #0455, Electrical and Computer Engineering, Bachelor of Science in Electrical Engineering, effective Fall 2013. DC #0456, Electrical and Computer Engineering, Bachelor of Science in Computer Engineering, effective Fall 2013. DC #0466, Materials Science and Engineering, Minor in Materials Science and Engineering, effective Fall 2013. DC #0467, Psychological Science, Bachelor of Arts in Psychology and Bachelor of Science in Psychology, effective Fall 2013. DC #0468, Psychological Science, Bachelor of Science in Psychology and Bachelor of Science in Psychology with Secondary Education Emphasis, effective Fall 2013. DC #0469, Civil, Architectural and Environmental Engineering, Bachelor of Science in Civil Engineering, effective Fall 2013. DC #0470, Civil, Architectural and Environmental Engineering, Bachelor of Science in Civil Engineering, effective Fall 2013. DC #0471, Information Science and Technology, Minor in Digital Supply Chain Management, effective Fall 2013. DC #0472, Manufacturing Engineering, Master of Science in Manufacturing Engineering, effective Fall 2013. Page 1 Office of the Registrar • 103 Parker Hall • 300 West 13 th Street • Rolla, MO 65409-0930 Phone: 573-341-4181 • Fax: 573-341-4362 • Email: [email protected] • Web: http://registrar.mst.edu An equal opportunity institution DC #0473, Mechanical and Aerospace Engineering, Bachelor of Science in Mechanical Engineering, effective Fall 2013. Review of submitted CC forms: CC #8370, Computer Engineering 202, Cooperative Engineering Training, effective Fall 2013. CC #8371, Electrical Engineering 202, Cooperative Engineering Training, effective Fall 2013.
    [Show full text]
  • High-Speed Programmable Photonic Circuits in a Cryogenically Compatible, Visible-NIR 200 Mm CMOS Architecture [Note] Mark Dong,1,2,6 Genevieve Clark,1,2 Andrew J
    High-speed programmable photonic circuits in a cryogenically compatible, visible-NIR 200 mm CMOS architecture [note] Mark Dong,1,2,6 Genevieve Clark,1,2 Andrew J. Leenheer,3 Matthew Zimmermann,1 Daniel Dominguez,3 Adrian J. Menssen,2 David Heim,1 Gerald Gilbert,2,4,7 Dirk Englund,2,5,8 and Matt Eichenfield3,9 1The MITRE Corporation, 202 Burlington Road, Bedford, Massachusetts 01730, USA 2Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA 3Sandia National Laboratories, P.O. Box 5800 Albuquerque, New Mexico, 87185, USA 4The MITRE Corporation, 200 Forrestal Road, Princeton, New Jersey 08540, USA 5Brookhaven National Laboratory, 98 Rochester St, Upton, New York 11973, USA [email protected] [email protected] [email protected] [email protected] Summary Recent advances in photonic integrated circuits (PICs) have enabled a new generation of “programmable many-mode interferometers” (PMMIs) realized by cascaded Mach Zehnder Interferometers (MZIs) capable of universal linear-optical transformations on N input-output optical modes. PMMIs serve critical functions in photonic quantum information processing, quantum-enhanced sensor networks, machine learning and other applications. However, PMMI implementations reported to date rely on thermo-optic phase shifters, which limit applications due to slow response times and high power consumption. Here, we introduce a large-scale PMMI platform, based on a 200 mm CMOS process, that uses aluminum nitride (AlN) piezo-optomechanical actuators coupled to silicon nitride (SiN) waveguides, enabling low-loss propagation with phase modulation at greater than 100 MHz in the visible to near-infrared wavelengths. Moreover, the vanishingly low holding-power consumption of the piezo-actuators enables these PICs to operate at cryogenic temperatures, paving the way for a fully integrated device architecture for a range of quantum applications.
    [Show full text]
  • Nanotechnology, Information Storage, and Applied Physics
    Nanotechnology,Nanotechnology, InformationInformation Storage,Storage, andand AppliedApplied PhysicsPhysics T.E. Schlesinger Director, Data Storage Systems Center Carnegie Mellon University Pittsburgh, PA, USA 30 November 2004 OutlineOutline Limits in information storage systems and IC fabrication technology are being approached THESE ARE REAL but are not fundamental in the sense of insurmountable laws of nature. Information storage today is an application of nanotechnology. Further advances in nanotechnology will bring unprecedented storage capacity that will fundamentally change the way we think about information. The integration of information storage and information processing will create a new paradigm to take us beyond CMOS technology. A Report from the U.S. National Science Foundation Blue Ribbon Panel on Cyberinfrastructure Daniel E. Atkins The University of Michigan Chair, NSF Panel on Cyberinfrastructure January 2003 “….cyberinfrastructure refers to infrastructure based upon distributed computer, information and communication technology. If infrastructure is required for an industrial economy, then we could say that cyberinfrastructure is required for a knowledge economy….. The base technologies underlying cyberinfrastructure are the integrated electro- optical components of computation, storage, and communication that continue to advance in raw capacity at exponential rates.” TheThe NeedNeed forfor StorageStorage New stored information grew about 30% a year between 1999 and 2002. Information flows through electronic channels -- telephone, radio, TV, and the Internet -- contained almost 18 exabytes (exabyte=1018 bytes) of new information in 2002, three and a half times more than is recorded in storage media. Ninety eight percent of this total is the information sent and received in telephone calls - including both voice and data on both fixed lines and wireless.
    [Show full text]
  • PMQ29 Optomechanics and Electromechanics: Physics and Applications
    PMQ29 " Optomechanics and Electromechanics: Physics and Applications" Organisateurs : Pierre-François Cohadon, Daniel Lanzillotti-Kimura, Pierre Verlot Parrainage ou lien avec des sociétés savantes, des GDR ou autres structures : Parrainage : GdR Optomécanique et Nanomécanique Quantique (MecaQ) Autres liens : GdR Ondes Gravitationnelles, GdR IQFA, GdR Ondes, GdR Meso, GdR Graphene & Co Résumé Optomechanics is the field of physics that investigates the reciprocal interaction between mechanical motion and the electromagnetic field (1). Originally driven by questions such as fundamental processes in quantum measurements, and the extent of quantum principles to the macroscopic scale (2), the field has expanded to a variety of fundamental and technological challenges. These notably include nanomechanical sensors (3), quantum transducers(4), quantum hybrid systems (5,6), nano-phononics (7), ultra-fast opto-acoustic platforms (8), thermodynamics (9,10) and all the corresponding applications (11–14). 25 years after its emergence, Optomechanics establishes as an important field of research worldwide. The rapid and impressive progress, including the first demonstration of optomechanical systems operating in the quantum regime in the early 2010’s (15,16), are driving major innovation and technological renewal, with a strong interdisciplinary impact. The mini-colloquium ‘Optomechanics and Electromechanics: Physics and Applications’ aims at reviewing the interdisciplinary nature of our field, ranging from quantum devices for information technology to nanomechanical bio-sensing. It will also represent a unique occasion for early-stage researchers to discover the community and present their own contribution, opening new opportunities in a rapidly evolving field. Figure 1 Optomechanics : from the kilometre down to the nanometre scale. (a) Photograph of the VIRGO interferometer (19).
    [Show full text]
  • Educational Program Profile «Electromechanics» from Speciality 141 «Power Engineering, Electrical Engineering and Electromechanics»
    Educational program Profile «Electromechanics» from speciality 141 «Power Engineering, Electrical Engineering and Electromechanics» 1 – General Information The official name of Electromechanics educational program Specialty 141 Power Engineering, Electrical engineering and Electromechanics Branch of knowledge 14 Electrical Engineering Higher education Bachelor, bachelor in power engineering, electrical engineering and level and electromechanics qualification name Type of diploma and Bachelor's degree, single, 240 ECTS credits, duration of training 3 years 10 volume of educational months program Availability of Ministry of Education and Science of Ukraine, certificate of accreditation accreditation УД № 21008298, Validity period to 01.07.2028 Cycle/Level First (bachelor) level of the NRC of Ukraine – 7 level FQ-EHEA – First cycle ЕQF-LLL – 6 Level Requirements to the Having a Junior Bachelor’s degree level of education of General rules for entry requirements entrant Language (s) of Ukrainian teaching Validity of 5 Years educational program 2 – Aim of educational Program Ability to solve specialized tasks and solve practical problems during professional activity in the field of electricity, electrical engineering and electromechanics or in training, which involves the use of theories and methods of physics and of engineering sciences and are characterized by complex and uncertain conditions. 3 – Characteristics of educational Program Domain Area of electrical Engineering: Power Engineering, Electrical engineering, electromechanics. Objects
    [Show full text]
  • Electrical and Computer Engineering
    Electrical and Computer Engineering Student Handbook 2018-2019 Dept. of Electrical and Computer Engineering University of Massachusetts Lowell N U U. o P M One University Ave S n er a - . PA P s m Ball 301 P s ro o it I L D Lowell, MA 01854 s f # i o t t a 6 w O (978) 934–3300 Fax: (978) 934-3027 g 9 e r e g ll web page: www.uml.edu/Engineering/Electrical-Computer/ 68 Academic Schedule- Fall 2018 Sep. 1 Residence halls open for new students Sep. 2 Residence halls open for returning students Sep. 3 Labor Day (university closed) Sep. 4 Convocation Sep. 5 Fall classes begin. Drop-add period begins. Sep. 11 Last day for undergraduate students to add a course without a permission number. Last day for instructors to publish course and attendance requirements for class members. Sep. 18 Last Day to (1) Add a course with a permission number (2) Drop a course without record (3) Change enrollment status from: Audit to Credit; Credit to Audit; “Pass-No Credit” to Letter Grade; Letter Grade to “Pass-No Credit” Note: No Refunds after this date Oct. 8 Columbus Day (University Closed) Oct. 11 Monday Class Schedule Oct. 17 Mid-Semester: at least one evaluation required in each course Oct. 22 Faculty advising period begins. Students check SiS for enrollment appointments. First day for seniors who anticipate completion of degree requirements by the end of May or the end of August to confer with faculty advisors and to file Programs of Baccalaureate Studies (DIG form).
    [Show full text]