Electromechanical Dynamics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Controlling Phonons and Photons at the Wavelength-Scale: Silicon Photonics Meets Silicon Phononics
1 Controlling phonons and photons at the wavelength-scale: silicon photonics meets silicon phononics AMIR H. SAFAVI-NAEINI1,D RIES VAN THOURHOUT2,R OEL BAETS2, AND RAPHAËL VAN LAER1,2 1Department of Applied Physics and Ginzton Laboratory, Stanford University, USA 2Photonics Research Group (INTEC), Department of Information Technology, Ghent University–imec, Belgium .Center for Nano- and Biophotonics, Ghent University, Belgium Compiled October 9, 2018 Radio-frequency communication systems have long used bulk- and surface-acoustic-wave de- vices supporting ultrasonic mechanical waves to manipulate and sense signals. These devices have greatly improved our ability to process microwaves by interfacing them to orders-of- magnitude slower and lower loss mechanical fields. In parallel, long-distance communications have been dominated by low-loss infrared optical photons. As electrical signal processing and transmission approaches physical limits imposed by energy dissipation, optical links are now being actively considered for mobile and cloud technologies. Thus there is a strong driver for wavelength-scale mechanical wave or “phononic” circuitry fabricated by scalable semiconduc- tor processes. With the advent of these circuits, new micro- and nanostructures that combine electrical, optical and mechanical elements have emerged. In these devices, such as optomechan- ical waveguides and resonators, optical photons and gigahertz phonons are ideally matched to one another as both have wavelengths on the order of micrometers. The development of phononic circuits has thus emerged as a vibrant field of research pursued for optical signal pro- cessing and sensing applications as well as emerging quantum technologies. In this review, we discuss the key physics and figures of merit underpinning this field. -

Is EE Right for You?
Erik Jonsson School of Engggineering and The Un ivers ity o f Texas a t Da llas Computer Science Is EE Right for You? • “Toto, I have a feeling we’re not in Kansas anymore.” • Now that you are here, diii?id you make the right choice? • Electrical engineering is a challenging and satisfying profession. That does not mean it is easy. In fact, with the possible exceptions of medicine or law, it is the MOST difficult. • There are some things you need to consider if you really, really want to be an engineer. • We will consider a few today. EE 1202 Lecture #1 – Why Electrical Engineering? 1 © N. B. Dodge 01/12 Erik Jonsson School of Engggineering and The Un ivers ity o f Texas a t Da llas Computer Science Is EE Right for You (2)? • Why did you decide to be an electrical engineer? – Parents will pay for engineering education (it’s what they want). – You like math and science. – A relative is an engineer and you like him/her. – You want to challenge yourself, and engineering seems challenging. – You think you are creative and love technology. – You want to make a difference in society . EE 1202 Lecture #1 – Why Electrical Engineering? 2 © N. B. Dodge 01/12 Erik Jonsson School of Engggineering and The Un ivers ity o f Texas a t Da llas Computer Science The High School “Science Student” Problem • In high school, you were FAR above the average. – And you probably didn’t study too hard, right? • You liked science and math, and they weren’t terribly hard. -

Electrical Engineering Technology
Electrical Engineering Technology Electrical Engineering Program Accreditation The Electrical Engineering Technology program at Central Piedmont is accredited by the Engineering Technology Accreditation Commission Technology (TAC) of the Accreditation Board of Engineering and Technology (ABET). The Associate in Applied Science degree in Electrical Engineering How to Apply: Technology has been specifically designed to prepare individuals to Complete a Central Piedmont admissions application through Get become advanced technicians in the workforce. Started on the Central Piedmont website. Electrical Engineering Technicians (Associates degree holders) typically build, install, test, troubleshoot, repair, and modify developmental and Contact Information production electronic components, equipment, and systems such as For questions about the program or for assistance as a student in the industrial/computer controls, manufacturing systems, instrumentation program, contact faculty advising. The Electrical Engineering Technology systems, communication systems, and power electronic systems. program is in the Engineering Technology Division. For additional information, visit the Electrical Engineering Technology website or call the A broad-based core of courses ensures that students develop the skills Program Chair at 704.330.6773. necessary to perform entry-level tasks. Emphasis is placed on developing the ability to think critically, analyze, and troubleshoot electronic systems. General Education Requirements Beginning with electrical fundamentals, course work progressively ENG 111 Writing and Inquiry 3.0 introduces electronics, 2D Computer Aided Design (CAD), circuit Select one of the following: 3.0 simulation, solid-state fundamentals, digital concepts, instrumentation, C++ programming, microprocessors, programmable Logic Controllers ENG 112 Writing and Research in the Disciplines (PLCs). Other course work includes the study of various fields associated ENG 113 Literature-Based Research with the electrical/electronic industry. -

Electrical Engineering Engineering
College of Electrical Engineering Engineering The undergraduate electrical engineering degree program seeks to produce gradu- Second Semester ates who are trained in the theory and practice of electrical and computer engineering EE 468G Introduction to Engineering Electromagnetics ........................................ 4 and are well prepared to handle the professional and leadership challenges of their Elective EE Laboratory [L] ...................................................................................... 2 careers. The program allows students to specialize in high performance and embed- Engineering/Science Elective [E] ............................................................................ 3 ded computing, microelectronics and nanotechnology, power and energy, signal Technical Elective [T] ............................................................................................. 3 processing and communications, high frequency circuits and fields, and control UK Core – Citizenship - USA .................................................................................. 3 systems, among others. Senior Year Degree Requirements The following curriculum meets the requirements for a B.S. in Electrical Engineering, First Semester Hours provided the student satisfies UK Core requirements and graduation requirements EE/CPE 490 ECE Capstone Design I† ..................................................................... 3 of the College of Engineering. EE Technical Elective* ........................................................................................... -

Electrical and Computer Engineering: Past, Present, and Future
Electrical and Computer Engineering: Past, Present, and Future Randy Berry1, chair, Department of Electrical and Computer Engineering The field of electrical and computer engineering (ECE) has had an enormously successful history. This field has pushed the frontiers of fundamental research, led to the emergence of entirely new disciplines, and revolutionized our daily lives. ECE departments2 are found in nearly every engineering school and have historically been one of the larger departments both in terms of faculty and student enrollments. Academically, a strong ECE department is highly correlated with the reputation of an engineering school. Of the top 10 engineering schools in the latest US News and World Report rankings of graduate programs, nine have top 10 ranked ECE programs. Nevertheless, ECE is a field that finds itself facing challenges. In this paper, we will look to the field’s past issues and note how the field repeatedly reinvented itself to push to new heights. Finally, we argue that the time is ripe for another reinvention and show how aspects of such a reinvention are already emerging. Areas such as machine learning and data science, the Internet of things, and quantum information systems provide promising directions for ECE — and embracing them provides a path to a bright future. The Present Situation In many ways, ECE is a victim of its own successes. Advances such as computer-aided design tools reduce the number of designers needed. The increased integration reflected in Moore’s law means that more functionality can be integrated into a single integrated circuit (IC), replacing the need for engineering to integrate multiple components in custom designs. -
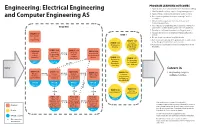
Electrical Engineering and Computer Engineering AS
PROGRAM LEARNING OUTCOMES Engineering: Electrical Engineering 1. Apply analysis tools and computer tools in problem solving. 2. Identify interdisciplinary aspects of engineering projects. 3. Apply software engineering principles and procedures. and Computer Engineering AS 4. Do computer algorithm development using C and C++ techniques. 5. Understand the operation and control of electrical measuring equipment. 6. Use computer programming skills to develop software for REQUIRED automation, decision making and control of equipment. 7. Develop test software for evaluation of digital circuits. ENGIN 110 8. Analyze the operation of small scale digital and analog TAKE 1 circuits. Introduction to 9. Design simple operational amplifier circuits. Engineering ENGTC 126 10. Demonstrate knowledge of magnetism and its applications in the design of transformers and actuators. ENGIN 120 Computer Engineering Aided Design 11. Assemble and test digital and analog circuits from circuit Drawing and Drafting – diagrams. AutoCAD COMSC 165 CHEM 120 COMSC 210 ENGIN 230 Advanced Program General pre req Introduction Programming Design College to Circuits and with C and and Data Chemistry I Devices ENGIN 121 C++ Structures ENGIN 135 Engineering Programming Drawing/ DVC II DVC I.B. for Scientists Descriptive pre req and Engineers Geometry Entry Careers in MATH 192 MATH 193 MATH 292 MATH 294 ENGIN 136 • Engineering design in Analytic pre req Analytic pre req Analytic pre req Differential Computer Geometry Geometry and Geometry and multiple disciplines Equations Programming and Calculus I Calculus II Calculus III for Engineers Using MATLAB* DVC I.B. DVC I.B. DVC I.B. DVC I.B. DVC I.C. DVC I.C. DVC I.C. -

Introduction to Electrical Engineering
Revision: 02/16/01 SUMMER INSTITUTE FOR ENGINEERING AND TECHNOLOGY EDUCATION ELECTRICAL ENGINEERING INTRODUCTION TO ELECTRICAL ENGINEERING CONCEPT This module explains some of the details about the work in which various Electrical Engineering specialties engage. OBJECTIVES 1. To expose the readers to the type of work Electrical Engineers do. 2. To give the readers an idea about the courses the students would require to take to pursue a degree in Electrical Engineering. 3. To explain about the career opportunities for Electrical Engineers. SCIENCE PROCESS SKILLS • Informing • Inquiring • Exploring AAAS SCIENCE BENCHMARKS: • 1B Scientific Inquiry • 12D Communication Skills • 3C Issues of Technology SCIENCE EDUCATION CONTENT STANDARDS (NRC) Grades 5-8: Grades 9-12: • Communications • Technology • Identify disciplines in Electrical Engineering STATE SCIENCE CURRICULUM FRAMEWORKS: Grades 5-8: 1.1.9, 1.1.19, 2.1.8, 2.1.11 Grades 9-12: 1.1.19 The Summer Institute for Engineering and Technology Education, University of Arkansas 1995. All rights reserved. ELECTRICAL ENGINEERING INTRODUCTION 2 INTRODUCTION Electrical Engineering implies electricity, which has flowed into every aspect of our lives. Electricity supplies power to run appliances, heavy machinery, and lights. Electricity also encompasses communications such as the telephone, radio, and television and other consumer electronic devices. And, of course, electronics is changing everything around us every day, through such pervasive devices as hand-held calculators, computers, and controllers that help operate automobiles, airplanes, and homes. Electrical Engineering is the largest engineering profession. HISTORY William Gilbert, an english scientist, characterized magnetism and static electricity around the year 1600, and Alexander Volta discovered that an electric current could be made to flow in 1800. -

Electrical Engineering Curriculum International Overview
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by UPCommons. Portal del coneixement obert de la UPC 2008 Electrical Engineering Curriculum International Overview Josep Miquel Jornet, Eduard Alarcón, Elisa Sayrol International Affairs Office and Dean’s office – Telecom BCN UPC 14/07/2008 2 I. Overview of the Electrical Engineering Curriculum in some of the main universities in North America Massachusetts Institute of Technology http://www.eecs.mit.edu/ug/brief‐guide.html#bach http://www.eecs.mit.edu/ug/primer.html#intro http://www.eecs.mit.edu/ug/programs.html These are the degrees related to Electrical Engineering and Computer Science offered at MIT: Bachelors’ Degrees • Course VI‐1/VI‐1A: A four‐year accredited program leading to the S.B. degree Bachelor of Science in Electrical Science and Engineering. • Course VI‐2/VI‐2A: A four‐year accredited program which permits a broad selection of subjects from electrical engineering and computer science leading to the S.B. degree Bachelor of Science in Electrical Engineering and Computer Science. • Course VI‐3/VI‐3A: A four‐year accredited program leading to the S.B. degree Bachelor of Science in Computer Science and Engineering. Masters’ Degrees • Course VI‐P / VI‐PA: A five‐year program leading to the M.Eng. degree Master of Engineering in Electrical Engineering and Computer Science and simultaneously to one of the three S.B.'s. This degree is available only to M.I.T. EECS undergraduates. It is an integrated undergraduate/graduate professional degree program with subject requirements ensuring breadth and depth. -

Methods of Using Mobile Internet Devices in the Formation of The
217 Methods of using mobile Internet devices in the formation of the general scientific component of bachelor in electromechanics competency in modeling of technical objects Yevhenii O. Modlo1[0000-0003-2037-1557], Serhiy O. Semerikov2,3,4[0000-0003-0789-0272], Stanislav L. Bondarevskyi3[0000-0003-3493-0639], Stanislav T. Tolmachev3[0000-0002-5513-9099], Oksana M. Markova3[0000-0002-5236-6640] and Pavlo P. Nechypurenko2[0000-0001-5397-6523] 1 Kryvyi Rih Metallurgical Institute of the National Metallurgical Academy of Ukraine, 5, Stephana Tilhy Str., Kryvyi Rih, 50006, Ukraine [email protected] 2 Kryvyi Rih State Pedagogical University, 54, Gagarina Ave., Kryvyi Rih, 50086, Ukraine [email protected], [email protected] 3 Kryvyi Rih National University, 11, Vitaliy Matusevych Str., Kryvyi Rih, 50027, Ukraine [email protected], [email protected], [email protected] 3 Institute of Information Technologies and Learning Tools of NAES of Ukraine, 9, M. Berlynskoho Str., Kyiv, 04060, Ukraine Abstract. An analysis of the experience of professional training bachelors of electromechanics in Ukraine and abroad made it possible to determine that one of the leading trends in its modernization is the synergistic integration of various engineering branches (mechanical, electrical, electronic engineering and automation) in mechatronics for the purpose of design, manufacture, operation and maintenance electromechanical equipment. Teaching mechatronics provides for the meaningful integration of various disciplines of professional and practical training bachelors of electromechanics based on the concept of modeling and technological integration of various organizational forms and teaching methods based on the concept of mobility. Within this approach, the leading learning tools of bachelors of electromechanics are mobile Internet devices (MID) – a multimedia mobile devices that provide wireless access to information and communication Internet services for collecting, organizing, storing, processing, transmitting, presenting all kinds of messages and data. -
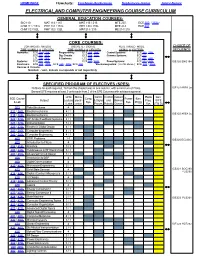
Electrical and Computer Engineering Course
HOMEPAGE Flowcharts: Freshman-Sophomore Sophomore-Junior Junior-Senior ELECTRICAL AND COMPUTER ENGINEERING COURSE CURRICULUM GENERAL EDUCATION COURSES: BIO 110 MAT 114 / 115 MAT 116 / 216 MTE 207 ECE 302 / 352L* CHM 111 / 151L PHY 131 / 151L PHY 133 / 153L MTE 214 ECE 311 CHM 112 / 152L PHY 132 / 132L MAT 214 / 215 ME 214 / 215 CORE COURSES: CONTINOUS / ANALOG DISCRETE / DIGITAL REAL / MIXED MODE CHOICE OF TIME SIGNALS & CIRCUITS TIME SIGNALS & CIRCUITS SIGNAL & SYSTEMS SEQUENCE Networks: ECE 109 / 129L Programming: ECE 114 , 164L Control Systems: ECE 309 , 359L ECE 207 , 252L Dig. Circuits ECE 204 , 244L Commu. Systems: ECE 315 ECE 209 , 253L & Systems: ECE 308 ECE 405 , 445L Systems: ECE 307 , 357L ECE 341 / 391L Power Systems: ECE 310 / 360L IGE120 ENG104 Electronic ECE 220 , 270L , ECE 320 , 370L, ECE 330 *Electromagnetics: ( in GE above ) ECE 302 / 352L Devices & Circuits: Notation: / and , indicate co-requisiste or not respectively SPECIFIED PROGRAM OF ELECTIVES (SPES) 20 Units for each required, 16 from the shaded ares in one column, with a minimum of 2 labs. IGE121AREA 3a General SPE requires at least 5 units each from 2 of the SPE Columns with advisors approval. Units Micro- Comm. Control Instrum Radio Gen. ECE Course Comp. Power Illum. Subject Lecture electr- & Signal and Biomed Freq. S P E & Lab Sys. Sys. Engg / Labs onics Proces. Robotic Ocean Sys. (T B D) 303 Data Structures 4 317 / 367L Electromechanics 4 / 1 IGE122 AREA 3c 318 / 368L Electromechanics 4 / 1 322 / 372L OP Amps./Feedback Systems 4 / 1 323 / 373L Instrumentation -

Electromechanical Motion Fundamentals
Electromechanical Motion Fundamentals • Electric Machine – device that can convert either mechanical energy to electrical energy or electrical energy to mechanical energy – mechanical to electrical: generator – electrical to mechanical: motor – all practical motors and generators convert energy from one form to another through the action of a magnetic field • Transformer – device that converts ac electric energy at one voltage level to ac electric energy at another voltage level Sensors & Actuators in Mechatronics K. Craig Electromechanical Motion Fundamentals 1 – It operates on the same principles as generators and motors, i.e., it depends on the action of a magnetic field to accomplish the change in voltage level • Motors, Generators, and Transformers are ubiquitous in modern daily life. Why? – Electric power is: • Clean • Efficient • Easy to transmit over long distances • Easy to control • Environmental benefits Sensors & Actuators in Mechatronics K. Craig Electromechanical Motion Fundamentals 2 • Purpose of this Study – provide basic knowledge of electromechanical motion devices for mechatronic engineers – focus on electromechanical rotational devices commonly used in low-power mechatronic systems • permanent magnet dc motor • brushless dc motor • stepper motor • Topics Covered: – Magnetic and Magnetically-Coupled Circuits – Principles of Electromechanical Energy Conversion Sensors & Actuators in Mechatronics K. Craig Electromechanical Motion Fundamentals 3 References • Electromechanical Motion Devices, P. Krause and O. Wasynczuk, McGraw Hill, 1989. • Electromechanical Dynamics, H. Woodson and J. Melcher, Wiley, 1968. • Electric Machinery Fundamentals, 3rd Edition, S. Chapman, McGraw Hill, 1999. • Driving Force, The Natural Magic of Magnets, J. Livingston, Harvard University Press, 1996. • Applied Electromagnetics, M. Plonus, McGraw Hill, 1978. • Electromechanics and Electric Machines, S. Nasar and L. Unnewehr, Wiley, 1979. -

Electronics and Electrical Engineering Laboratory
NISTR 7568 Programs, Activities, and Accomplishments March 2009 NISTIR 7568 ELECTRONICS AND ELECTRICAL ENGINEERING LABORATORY U.S. Department of Commerce Gary Locke, Secretary National Institute of Standards and Technology March 2009 Patrick D. Gallagher, Deputy Director INDEX Electronics and Electrical Engineering Laboratory at a Glance . 6 Director’s Message . 7 EEEL Strategic Technical Area: Energy . 8 EEEL Strategic Technical Area: Bioelectronics . 9 EEEL Strategic Technical Area: Nanotechnology. 10 EEEL Strategic Technical Area: Spintronics. 11 EEEL Strategic Technical Area: Homeland Security . 12 Office of Law Enforcement Standards . 14 Office of Microelectronics Programs . 16 Semiconductor Electronics Division . 19 Power Device and Thermal Metrology . 20 Micro-Nano-Technology (MNT) . 22 Nanobiotechnology . 24 CMOS Device and Reliability . 26 Macro Electronics . 28 Nanoelectronic Device Metrology. 30 Infrastructure for Integrated Electronics Design and Manufacturing . 32 Knowledge Facilitation . 34 Optoelectronics Division. 37 Display Metrology . 38 Laser Radiometry. 40 High-Speed Measurements. 42 Fiber Sources and Applications . 44 Quantum Information and Terahertz Technology . 46 Nanostructure Fabrication and Metrology . 48 Semiconductor Growth and Devices. 50 Optical Materials Metrology . 52 Quantum Electrical Metrology Division . 55 Quantum Voltage System Development and Dissemination . 56 Metrology of the Ohm . 58 Quantum Conductance/Graphene-Based Quantum Metrology . 60 AC-DC Difference . 62 Farad and Impedance Metrology . 64 Electronic Kilogram . 66 Electric Power Metrology and the Smart Grid . 68 Quantum Sensors. 70 Quantum Information and Measurements . 72 Quantum Magnetic Sensors and Materials. 74 Electromagnetics Division. 77 This document describes Advanced High Frequency Devices . 78 the technical programs of the Advanced Materials Metrology. 80 Fundamental Guided-Wave Metrology . 82 laboratory. Antenna Metrology. 84 Field Parameter Metrology .