DOCSLIB.ORG

Linear Regression Using Ordinary Least Squares

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Linear Regression Using Ordinary Least Squares Simple Linear Regression Using Ordinary Least Squares Purpose: To approximate a linear relationship with a line. Reason: We want to be able to predict Y using X. Definition: The Least Squares Regression (LSR) line is the line with the smallest sum of square residuals smaller than any other line. That is, we want to measure closeness of the line to the points. The LSR line uses vertical distance from points to a line. A residual is the vertical distance from a point to a line. Equations: The true line for the population parameter: y = α + βx Note: We are trying to estimate this equation. We obtain a sample and estimate an approximation: yˆ = a + bx + E Estimate y Predict α = y-intercept Predict β = slope x = The independent variable. E = Epsilon or the error. These are random errors of measurement. Check the Assumptions: 1. No outliers. 2. Residuals follow a normal distribution with a mean = 0. 3. Residuals should be randomly scattered. Note: For #2, produce a histogram of the standardized residuals to see if they are normal. Hypotheses for the Correlation Coefficient (R): A measure of how close residuals are to the regression line. H0: ρ = 0 H1: ρ ≠ or < or > 0 Coefficient of Determination = R2 Range 0 – 1 0 ≤ r 2 ≤ 1 R2 = An effect size measure and yields the percentage of the variation in the Y values explained by X. Adjusted R2: Adjusts for R2’s upward bias and is a variance accounted for effect size measure. 2 Adj. R = .40 40% of variation in Y is explained by the regression line and dependent on X. SSR What’s explained by regression line SSRegression R2 = 2 SST (variability in y values or Σ()y − y SEE: The square root of the Mean Square Residual is the same as the Standard Error of the Estimate, which is the amount of error in the model measured in DV units. The higher the Adj. R2 value, the smaller the amount of error in the model (i.e., the smaller the value of the SEE) and the more stability the model will have upon replication. F Test Hypotheses: H0: The regression does not explain a significant proportion of the variance in Y. H1: The regression works and does explain a significant proportion of the variance in Y. ANOVA Results: How close the points are to the line: 1. SSR/SSE = Sum of Squared Residuals or SSE (E = Errors): Variation attributed to factors other than the relationship between X and Y. 2. SST = Sum of Squares Total: A measure of the total variability of your Y values around their Mean Y (i.e., how much Y values vary). 3. SSR = Sums of Squares Regression: The explained variation attributed to the relationship between X and Y. Note: We want a large SSRegression & Small SSE. That is, the points are close to the line and the line does a good job of predicting. Hypotheses for the Slope: H0: β = 0 No linear relationship H1: β ≠ or < or > 0 Linear relationship Test statistic = The distribution of β (slope) 1. The distribution of β is normal. 2. Mean = β Se Se = measure of the variation of the points around the line. 3. S.D. = 2 Σ()x − x SSE (# of parameters; thing you’re estimating) n − 2 B t = Se Hypotheses for the Intercept: H0: α (y-intercept) = 0 H1: α ≠ or < or > 0 a t = Se Confidence Intervals for B (Unstandardized Coefficient) B ±1.645or1.96or2.58α (Se) 2 Simple Linear Regression: Example 1 The linear model assumes that the relations between two variables can be summarized by a straight line. The X variable is often called the predictor and Y is often called the criterion. We often talk about the regression of Y on X, so that if we were predicting GPA from SAT we would talk about the regression of GPA on SAT. The regression problems that we deal with will use a line to transform values of X to predict values of Y. In general, not all of the points will fall on the line, but we will choose our regression line so as to best summarize the relations between X and Y. Suppose we measured the height and weight of a random sample of 10 adults in DeKalb. We want to predict weight from height in the population. Ht Wt 61 105 62 120 63 120 65 160 65 120 68 145 69 175 70 160 72 185 75 210 N=10 N=10 67 150 Mean 20.89 1155.5 Variance (s2) 4.57 33.99 SD (s) Correlation (r) = .94 For the regression of weight on height, we found: Y = -316.86 + 6.97(x), where -361.86 is the intercept (α ) and 6.97 is the slope ( β ). We could also write that weight is -316.86+6.97(height). The slope value means that for each inch we increase in height, we expect to increase approximately 7 pounds in weight. The intercept is the value of Y that we expect when X is zero. So if we had a person 0 inches tall, they should weigh -316.86 pounds (i.e., 6.97 *0 = 0; -316.86 + 0 = -316.86). Of course we do not find people who are zero inches tall and we do not find people with negative weight. Sometimes, in educational research, the value of the intercept will have no meaningful interpretation. Simple Linear Regression: Example 2 A. Predicted: Self-destructiveness = -108.92 + 22.33 Alcohol Unstandardized Regression Coefficients 22.33 Alcohol: We predict a 22.33 point increase in self-destructiveness for a one point increase in Alcohol when all other variables are held constant. B. Predicted: Self-destructiveness = 0.49 Alcohol Standardized Regression Coefficients 0.49 Alcohol: We predict a 0.49 standard deviation increase in self-destructiveness for a one standard deviation increase in Alcohol when all other variables are held constant. Simple Linear Regression: Example 3 The linear model tells us that each observed Y is composed of two parts, (1) a linear function of X, and (2) an error. We can use the regression line to predict values of Y given values of X. For any given value of X, we go straight up to the line, and then move horizontally to the left to find the value of Y. The predicted value of Y is called the predicted value of Y, and is denoted Y'. The difference between the observed Y and the predicted Y (Y-Y') is called a residual. The predicted Y part is the linear part. The residual is the error. N Ht Wt Y' Residual 1 61 105 108.19 -3.19 2 62 120 115.16 4.84 3 63 120 122.13 -2.13 4 65 160 136.06 23.94 5 65 120 136.06 -16.06 6 68 145 156.97 -11.97 7 69 175 163.94 11.06 8 70 160 170.91 -10.91 9 72 185 184.84 0.16 10 75 210 205.75 4.25 Mean 67 150 150.00 0.00 SD 4.57 33.99 31.85 11.89 Variance 20.89 1155.56 1014.37 141.32 Compare the numbers in the table for person 5 (height = 65, weight=120) to the same person on the graph. The regression line for X=65 is 136.06. The difference between the mean of Y and 136.06 is the part of Y due to the linear function of X. The difference between the line and Y is -16.06. This is the error part of Y, the residual. .
Load more

Recommended publications
  • A Generalized Linear Model for Principal Component Analysis of Binary Data
    A Generalized Linear Model for Principal Component Analysis of Binary Data Andrew I. Schein Lawrence K. Saul Lyle H. Ungar Department of Computer and Information Science University of Pennsylvania Moore School Building 200 South 33rd Street Philadelphia, PA 19104-6389 {ais,lsaul,ungar}@cis.upenn.edu Abstract they are not generally appropriate for other data types. Recently, Collins et al.[5] derived generalized criteria We investigate a generalized linear model for for dimensionality reduction by appealing to proper- dimensionality reduction of binary data. The ties of distributions in the exponential family. In their model is related to principal component anal- framework, the conventional PCA of real-valued data ysis (PCA) in the same way that logistic re- emerges naturally from assuming a Gaussian distribu- gression is related to linear regression. Thus tion over a set of observations, while generalized ver- we refer to the model as logistic PCA. In this sions of PCA for binary and nonnegative data emerge paper, we derive an alternating least squares respectively by substituting the Bernoulli and Pois- method to estimate the basis vectors and gen- son distributions for the Gaussian. For binary data, eralized linear coefficients of the logistic PCA the generalized model's relationship to PCA is anal- model. The resulting updates have a simple ogous to the relationship between logistic and linear closed form and are guaranteed at each iter- regression[12]. In particular, the model exploits the ation to improve the model's likelihood. We log-odds as the natural parameter of the Bernoulli dis- evaluate the performance of logistic PCA|as tribution and the logistic function as its canonical link.
    [Show full text]
  • Understanding Linear and Logistic Regression Analyses
    EDUCATION • ÉDUCATION METHODOLOGY Understanding linear and logistic regression analyses Andrew Worster, MD, MSc;*† Jerome Fan, MD;* Afisi Ismaila, MSc† SEE RELATED ARTICLE PAGE 105 egression analysis, also termed regression modeling, come). For example, a researcher could evaluate the poten- Ris an increasingly common statistical method used to tial for injury severity score (ISS) to predict ED length-of- describe and quantify the relation between a clinical out- stay by first producing a scatter plot of ISS graphed against come of interest and one or more other variables. In this ED length-of-stay to determine whether an apparent linear issue of CJEM, Cummings and Mayes used linear and lo- relation exists, and then by deriving the best fit straight line gistic regression to determine whether the type of trauma for the data set using linear regression carried out by statis- team leader (TTL) impacts emergency department (ED) tical software. The mathematical formula for this relation length-of-stay or survival.1 The purpose of this educa- would be: ED length-of-stay = k(ISS) + c. In this equation, tional primer is to provide an easily understood overview k (the slope of the line) indicates the factor by which of these methods of statistical analysis. We hope that this length-of-stay changes as ISS changes and c (the “con- primer will not only help readers interpret the Cummings stant”) is the value of length-of-stay when ISS equals zero and Mayes study, but also other research that uses similar and crosses the vertical axis.2 In this hypothetical scenario, methodology.
    [Show full text]
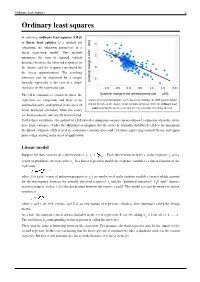
  • Ordinary Least Squares 1 Ordinary Least Squares
    Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β.
    [Show full text]
  • Ordinary Least Squares: the Univariate Case
    Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Ordinary Least Squares: the univariate case Clément de Chaisemartin Majeure Economie September 2011 Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises 1 Introduction 2 The OLS method Objective and principles of OLS Deriving the OLS estimates Do OLS keep their promises ? 3 The linear causal model Assumptions Identification and estimation Limits 4 A simulation & applications OLS do not always yield good estimates... But things can be improved... Empirical applications 5 Conclusion and exercises Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objectives Objective 1 : to make the best possible guess on a variable Y based on X . Find a function of X which yields good predictions for Y . Given cigarette prices, what will be cigarettes sales in September 2010 in France ? Objective 2 : to determine the causal mechanism by which X influences Y . Cetebus paribus type of analysis. Everything else being equal, how a change in X affects Y ? By how much one more year of education increases an individual’s wage ? By how much the hiring of 1 000 more policemen would decrease the crime rate in Paris ? The tool we use = a data set, in which we have the wages and number of years of education of N individuals. Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objective and principles of OLS What we have and what we want For each individual in our data set we observe his wage and his number of years of education.
    [Show full text]
  • Linear, Ridge Regression, and Principal Component Analysis
    Linear, Ridge Regression, and Principal Component Analysis Linear, Ridge Regression, and Principal Component Analysis Jia Li Department of Statistics The Pennsylvania State University Email: [email protected] http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Introduction to Regression I Input vector: X = (X1, X2, ..., Xp). I Output Y is real-valued. I Predict Y from X by f (X ) so that the expected loss function E(L(Y , f (X ))) is minimized. I Square loss: L(Y , f (X )) = (Y − f (X ))2 . I The optimal predictor ∗ 2 f (X ) = argminf (X )E(Y − f (X )) = E(Y | X ) . I The function E(Y | X ) is the regression function. Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Example The number of active physicians in a Standard Metropolitan Statistical Area (SMSA), denoted by Y , is expected to be related to total population (X1, measured in thousands), land area (X2, measured in square miles), and total personal income (X3, measured in millions of dollars). Data are collected for 141 SMSAs, as shown in the following table. i : 1 2 3 ... 139 140 141 X1 9387 7031 7017 ... 233 232 231 X2 1348 4069 3719 ... 1011 813 654 X3 72100 52737 54542 ... 1337 1589 1148 Y 25627 15389 13326 ... 264 371 140 Goal: Predict Y from X1, X2, and X3. Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Linear Methods I The linear regression model p X f (X ) = β0 + Xj βj .
    [Show full text]
  • Simple Linear Regression with Least Square Estimation: an Overview
    Aditya N More et al, / (IJCSIT) International Journal of Computer Science and Information Technologies, Vol. 7 (6) , 2016, 2394-2396 Simple Linear Regression with Least Square Estimation: An Overview Aditya N More#1, Puneet S Kohli*2, Kshitija H Kulkarni#3 #1-2Information Technology Department,#3 Electronics and Communication Department College of Engineering Pune Shivajinagar, Pune – 411005, Maharashtra, India Abstract— Linear Regression involves modelling a relationship amongst dependent and independent variables in the form of a (2.1) linear equation. Least Square Estimation is a method to determine the constants in a Linear model in the most accurate way without much complexity of solving. Metrics where such as Coefficient of Determination and Mean Square Error is the ith value of the sample data point determine how good the estimation is. Statistical Packages is the ith value of y on the predicted regression such as R and Microsoft Excel have built in tools to perform Least Square Estimation over a given data set. line The above equation can be geometrically depicted by Keywords— Linear Regression, Machine Learning, Least Squares Estimation, R programming figure 2.1. If we draw a square at each point whose length is equal to the absolute difference between the sample data point and the predicted value as shown, each of the square would then represent the residual error in placing the I. INTRODUCTION regression line. The aim of the least square method would Linear Regression involves establishing linear be to place the regression line so as to minimize the sum of relationships between dependent and independent variables.
    [Show full text]
  • Chapter 2: Ordinary Least Squares Regression
    Chapter 2: Ordinary Least Squares In this chapter: 1. Running a simple regression for weight/height example (UE 2.1.4) 2. Contents of the EViews equation window 3. Creating a workfile for the demand for beef example (UE, Table 2.2, p. 45) 4. Importing data from a spreadsheet file named Beef 2.xls 5. Using EViews to estimate a multiple regression model of beef demand (UE 2.2.3) 6. Exercises Ordinary Least Squares (OLS) regression is the core of econometric analysis. While it is important to calculate estimated regression coefficients without the aid of a regression program one time in order to better understand how OLS works (see UE, Table 2.1, p.41), easy access to regression programs makes it unnecessary for everyday analysis.1 In this chapter, we will estimate simple and multivariate regression models in order to pinpoint where the regression statistics discussed throughout the text are found in the EViews program output. Begin by opening the EViews program and opening the workfile named htwt1.wf1 (this is the file of student height and weight that was created and saved in Chapter 1). Running a simple regression for weight/height example (UE 2.1.4): Regression estimation in EViews is performed using the equation object. To create an equation object in EViews, follow these steps: Step 1. Open the EViews workfile named htwt1.wf1 by selecting File/Open/Workfile on the main menu bar and click on the file name. Step 2. Select Objects/New Object/Equation from the workfile menu.2 Step 3.
    [Show full text]
  • Application of General Linear Models (GLM) to Assess Nodule Abundance Based on a Photographic Survey (Case Study from IOM Area, Pacific Ocean)
    minerals Article Application of General Linear Models (GLM) to Assess Nodule Abundance Based on a Photographic Survey (Case Study from IOM Area, Pacific Ocean) Monika Wasilewska-Błaszczyk * and Jacek Mucha Department of Geology of Mineral Deposits and Mining Geology, Faculty of Geology, Geophysics and Environmental Protection, AGH University of Science and Technology, 30-059 Cracow, Poland; [email protected] * Correspondence: [email protected] Abstract: The success of the future exploitation of the Pacific polymetallic nodule deposits depends on an accurate estimation of their resources, especially in small batches, scheduled for extraction in the short term. The estimation based only on the results of direct seafloor sampling using box corers is burdened with a large error due to the long sampling interval and high variability of the nodule abundance. Therefore, estimations should take into account the results of bottom photograph analyses performed systematically and in large numbers along the course of a research vessel. For photographs taken at the direct sampling sites, the relationship linking the nodule abundance with the independent variables (the percentage of seafloor nodule coverage, the genetic types of nodules in the context of their fraction distribution, and the degree of sediment coverage of nodules) was determined using the general linear model (GLM). Compared to the estimates obtained with a simple Citation: Wasilewska-Błaszczyk, M.; linear model linking this parameter only with the seafloor nodule coverage, a significant decrease Mucha, J. Application of General in the standard prediction error, from 4.2 to 2.5 kg/m2, was found. The use of the GLM for the Linear Models (GLM) to Assess assessment of nodule abundance in individual sites covered by bottom photographs, outside of Nodule Abundance Based on a direct sampling sites, should contribute to a significant increase in the accuracy of the estimation of Photographic Survey (Case Study nodule resources.
    [Show full text]
  • The Simple Linear Regression Model
    The Simple Linear Regression Model Suppose we have a data set consisting of n bivariate observations {(x1, y1),..., (xn, yn)}. Response variable y and predictor variable x satisfy the simple linear model if they obey the model yi = β0 + β1xi + ǫi, i = 1,...,n, (1) where the intercept and slope coefficients β0 and β1 are unknown constants and the random errors {ǫi} satisfy the following conditions: 1. The errors ǫ1, . , ǫn all have mean 0, i.e., µǫi = 0 for all i. 2 2 2 2. The errors ǫ1, . , ǫn all have the same variance σ , i.e., σǫi = σ for all i. 3. The errors ǫ1, . , ǫn are independent random variables. 4. The errors ǫ1, . , ǫn are normally distributed. Note that the author provides these assumptions on page 564 BUT ORDERS THEM DIFFERENTLY. Fitting the Simple Linear Model: Estimating β0 and β1 Suppose we believe our data obey the simple linear model. The next step is to fit the model by estimating the unknown intercept and slope coefficients β0 and β1. There are various ways of estimating these from the data but we will use the Least Squares Criterion invented by Gauss. The least squares estimates of β0 and β1, which we will denote by βˆ0 and βˆ1 respectively, are the values of β0 and β1 which minimize the sum of errors squared S(β0, β1): n 2 S(β0, β1) = X ei i=1 n 2 = X[yi − yˆi] i=1 n 2 = X[yi − (β0 + β1xi)] i=1 where the ith modeling error ei is simply the difference between the ith value of the response variable yi and the fitted/predicted valuey ˆi.
    [Show full text]
  • Principal Component Analysis (PCA) As a Statistical Tool for Identifying Key Indicators of Nuclear Power Plant Cable Insulation
    Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2017 Principal component analysis (PCA) as a statistical tool for identifying key indicators of nuclear power plant cable insulation degradation Chamila Chandima De Silva Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Materials Science and Engineering Commons, Mechanics of Materials Commons, and the Statistics and Probability Commons Recommended Citation De Silva, Chamila Chandima, "Principal component analysis (PCA) as a statistical tool for identifying key indicators of nuclear power plant cable insulation degradation" (2017). Graduate Theses and Dissertations. 16120. https://lib.dr.iastate.edu/etd/16120 This Thesis is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Principal component analysis (PCA) as a statistical tool for identifying key indicators of nuclear power plant cable insulation degradation by Chamila C. De Silva A thesis submitted to the graduate faculty in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Major: Materials Science and Engineering Program of Study Committee: Nicola Bowler, Major Professor Richard LeSar Steve Martin The student author and the program of study committee are solely responsible for the content of this thesis. The Graduate College will ensure this thesis is globally accessible and will not permit alterations after a degree is conferred.
    [Show full text]
  • Generalized Linear Models
    CHAPTER 6 Generalized linear models 6.1 Introduction Generalized linear modeling is a framework for statistical analysis that includes linear and logistic regression as special cases. Linear regression directly predicts continuous data y from a linear predictor Xβ = β0 + X1β1 + + Xkβk.Logistic regression predicts Pr(y =1)forbinarydatafromalinearpredictorwithaninverse-··· logit transformation. A generalized linear model involves: 1. A data vector y =(y1,...,yn) 2. Predictors X and coefficients β,formingalinearpredictorXβ 1 3. A link function g,yieldingavectoroftransformeddataˆy = g− (Xβ)thatare used to model the data 4. A data distribution, p(y yˆ) | 5. Possibly other parameters, such as variances, overdispersions, and cutpoints, involved in the predictors, link function, and data distribution. The options in a generalized linear model are the transformation g and the data distribution p. In linear regression,thetransformationistheidentity(thatis,g(u) u)and • the data distribution is normal, with standard deviation σ estimated from≡ data. 1 1 In logistic regression,thetransformationistheinverse-logit,g− (u)=logit− (u) • (see Figure 5.2a on page 80) and the data distribution is defined by the proba- bility for binary data: Pr(y =1)=y ˆ. This chapter discusses several other classes of generalized linear model, which we list here for convenience: The Poisson model (Section 6.2) is used for count data; that is, where each • data point yi can equal 0, 1, 2, ....Theusualtransformationg used here is the logarithmic, so that g(u)=exp(u)transformsacontinuouslinearpredictorXiβ to a positivey ˆi.ThedatadistributionisPoisson. It is usually a good idea to add a parameter to this model to capture overdis- persion,thatis,variationinthedatabeyondwhatwouldbepredictedfromthe Poisson distribution alone.
    [Show full text]
  • Generalized Linear Models
    Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608) Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions • So far we've seen two canonical settings for regression. Let X 2 Rp be a vector of predictors. In linear regression, we observe Y 2 R, and assume a linear model: T E(Y jX) = β X; for some coefficients β 2 Rp. In logistic regression, we observe Y 2 f0; 1g, and we assume a logistic model (Y = 1jX) log P = βT X: 1 − P(Y = 1jX) • What's the similarity here? Note that in the logistic regression setting, P(Y = 1jX) = E(Y jX). Therefore, in both settings, we are assuming that a transformation of the conditional expec- tation E(Y jX) is a linear function of X, i.e., T g E(Y jX) = β X; for some function g. In linear regression, this transformation was the identity transformation g(u) = u; in logistic regression, it was the logit transformation g(u) = log(u=(1 − u)) • Different transformations might be appropriate for different types of data. E.g., the identity transformation g(u) = u is not really appropriate for logistic regression (why?), and the logit transformation g(u) = log(u=(1 − u)) not appropriate for linear regression (why?), but each is appropriate in their own intended domain • For a third data type, it is entirely possible that transformation neither is really appropriate. What to do then? We think of another transformation g that is in fact appropriate, and this is the basic idea behind a generalized linear model 1.2 Generalized linear models • Given predictors X 2 Rp and an outcome Y , a generalized linear model is defined by three components: a random component, that specifies a distribution for Y jX; a systematic compo- nent, that relates a parameter η to the predictors X; and a link function, that connects the random and systematic components • The random component specifies a distribution for the outcome variable (conditional on X).
    [Show full text]