Graphical Perception of Continuous Quantitative Maps: the Effects Of
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Sensory Memory Is Allocated Exclusively to the Current Event-Segment
Sensory memory is allocated exclusively to the current event-segment Item Type Article Authors Tripathy, Srimant P.; Ögmen, H. Citation Tripathy SP and Ögmen H (2018) Sensory memory is allocated exclusively to the current event-segment. Frontiers in Psychology. 9: 1435. Rights (c) 2018 The Authors. This is an Open Access article distributed under the Creative Commons CC-BY license (http:// creativecommons.org/licenses/by/4.0/) Download date 28/09/2021 02:42:01 Link to Item http://hdl.handle.net/10454/16722 ORIGINAL RESEARCH published: 07 September 2018 doi: 10.3389/fpsyg.2018.01435 Sensory Memory Is Allocated Exclusively to the Current Event-Segment Srimant P. Tripathy 1* and Haluk Ögmenˇ 2 1 School of Optometry and Vision Science, University of Bradford, Bradford, United Kingdom, 2 Department of Electrical and Computer Engineering, University of Denver, Denver, CO, United States The Atkinson-Shiffrin modal model forms the foundation of our understanding of human memory. It consists of three stores (Sensory Memory (SM), also called iconic memory, Short-Term Memory (STM), and Long-Term Memory (LTM)), each tuned to a different time-scale. Since its inception, the STM and LTM components of the modal model have undergone significant modifications, while SM has remained largely unchanged, Edited by: representing a large capacity system funneling information into STM. In the laboratory, Qasim Zaidi, visual memory is usually tested by presenting a brief static stimulus and, after a delay, University at Buffalo, United States asking observers to report some aspect of the stimulus. However, under ecological Reviewed by: Ronald A. Rensink, viewing conditions, our visual system receives a continuous stream of inputs, which University of British Columbia, Canada is segmented into distinct spatio-temporal segments, called events. -

A New Conceptualization of Human Visual Sensory-Memory
HYPOTHESIS AND THEORY published: 09 June 2016 doi: 10.3389/fpsyg.2016.00830 A New Conceptualization of Human Visual Sensory-Memory Haluk Ögmen˘ 1, 2* and Michael H. Herzog 3 1 Department of Electrical and Computer Engineering, University of Houston, Houston, TX, USA, 2 Center for Neuro-Engineering and Cognitive Science, University of Houston, Houston, TX, USA, 3 Laboratory of Psychophysics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland Memory is an essential component of cognition and disorders of memory have significant individual and societal costs. The Atkinson–Shiffrin “modal model” forms the foundation of our understanding of human memory. It consists of three stores: Sensory Memory (SM), whose visual component is called iconic memory, Short-Term Memory (STM; also called working memory, WM), and Long-Term Memory (LTM). Since its inception, shortcomings of all three components of the modal model have been identified. While the theories of STM and LTM underwent significant modifications to address these shortcomings, models of the iconic memory remained largely unchanged: A high capacity but rapidly decaying store whose contents are encoded in retinotopic coordinates, i.e., according to how the stimulus is projected on the retina. The fundamental shortcoming of iconic memory models is that, because contents are encoded in retinotopic coordinates, the iconic memory cannot hold any useful information under normal viewing conditions Edited by: when objects or the subject are in motion. Hence, half-century after its formulation, it Britt Anderson, remains an unresolved problem whether and how the first stage of the modal model University of Waterloo, Canada serves any useful function and how subsequent stages of the modal model receive Reviewed by: inputs from the environment. -

Perceptually-Motivated Graphics, Visualization and 3D Displays
Perceptually-Motivated Graphics, Visualization and 3D Displays Ann McNamara∗ Department of Visualization Texas A&M University Katerina Mania† Department of Electronic & Computer Engineering Technical University of Crete Marty Banks‡ Visual Space Perception Laboratory University of California, Berkeley Christopher Healey§ Department of Computer Science North Carolina State University May 18, 2010 ∗[email protected] †[email protected] ‡[email protected] §[email protected] Abstract This course presents timely, relevant examples on how researchers have leveraged perceptual information for optimization of rendering algorithms, to better guide design and presentation in (3D stereoscopic) display media, and for improved visualization of complex or large data sets. Each presentation will provide ref- erences and short overviews of cutting-edge current research pertaining to that area. We will ensure that the most up-to-date research examples are presented by sourcing information from recent perception and graphics conferences and journals such as ACM Transactions on Perception, paying particular attention work presented at the 2010 Symposium on Applied Perception in Graphics and Visualization. About the Lecturers Ann McNamara Department of Visualization Texas A&M University 3137 TAMU College Station, TX 77843-3137 +1-979-845-4715 [email protected] http://www.viz.tamu.edu/people/ann Ann McNamara received her undergraduate and graduate degrees from the Uni- versity of Bristol, UK. Anns research focuses on the advancement of computer graphics and scientific visualization through novel approaches for optimizing an individuals experience when creating, viewing and interacting with virtual spaces. She investigates new ways to exploit knowledge of human visual per- ception to produce high quality computer graphics and animations more effi- ciently. -

Visual Awareness Is Essential for Grouping Based on Mirror Symmetry
S S symmetry Article Visual Awareness Is Essential for Grouping Based on Mirror Symmetry Dina Devyatko 1,* and Ruth Kimchi 1,2,* 1 Institute of Information Processing and Decision Making, University of Haifa, Haifa 3498838, Israel 2 Department of Psychology, University of Haifa, Haifa 3498838, Israel * Correspondence: [email protected] or [email protected] (D.D.); [email protected] (R.K.) Received: 30 September 2020; Accepted: 10 November 2020; Published: 13 November 2020 Abstract: We examined whether symmetry-based grouping can take place in the absence of visual awareness. To this end, we used a priming paradigm, sandwich masking as an invisibility-inducing method, and primes and targets composed of two vertical symmetric or asymmetric lines. The target could be congruent or incongruent with the prime in symmetry. In Experiment 1, participants were presented with masked primes and clearly visible targets. In each trial, the participants performed a two-alternative discrimination task on the target, and then rated the visibility of the prime on a subjective visibility four-point scale (used to assess prime awareness). Subjectively invisible primes failed to produce response priming, suggesting that symmetry processing might depend on visual awareness. However, participants barely saw the prime, and the results for the visible primes were inconclusive, even when we used a conservative criterion for awareness. To rule out the possibility that our prime stimuli could not produce priming per se, we conducted a control visibility experiment (Experiment 2), in which participants were presented with unmasked, clearly visible primes and performed a target task. The results showed that our primes could elicit significant response priming when visible. -

Technical Restrictions of Computer-Manipulated Visual Stimuli and Display Units for Studying Animal Behaviour Sebastian A
Ethology CURRENT ISSUES – PERSPECTIVES AND REVIEWS Technical Restrictions of Computer-Manipulated Visual Stimuli and Display Units for Studying Animal Behaviour Sebastian A. Baldauf, Harald Kullmann & Theo C. M. Bakker Institute for Evolutionary Biology and Ecology, University of Bonn, Bonn, Germany Correspondence Abstract Sebastian A. Baldauf, Institute for Evolutionary Biology and Ecology, University of Bonn, Computer-manipulated visual stimuli are a well-established tool to An der Immenburg 1, D-53121 Bonn, experimentally study animal behaviour. They provide the opportunity Germany. to manipulate single or combined visual stimuli selectively, while other E-mail: [email protected] potentially confounding variables remain constant. A wide array of dif- ferent presentation methods of artificial stimuli has been used in recent Received: February 3, 2008 research. Furthermore, a wide range of basic hardware and software has Initial acceptance: March 17, 2008 Final acceptance: March 19, 2008 been used to conduct experiments. The outcomes of experimental trials (J. Kotiaho) using computer-manipulated visual stimuli differed among studies. Fail- ing or contradictory results were mostly discussed in a behavioural and doi: 10.1111/j.1439-0310.2008.01520.x ecological context. However, the results sometimes may be basically flawed due to methodological traps in the experimental design. Based on characteristics and restrictions of technical standards, we discuss which kinds of computer stimuli and visual display units are available today and their suitability for experimental trials when studying animal behaviour. A computer-manipulated stimulus displayed by a certain visual display unit may be accurate to investigate behaviour in a specific species, if various preconditions are met. -

Timbre Memory, Familiarity and Dissimilarity
Timbre Memory, Familiarity and Dissimilarity Lap Ian Lou Music Technology Area Department of Music Research Schulich School of Music McGill University Montreal, Canada June 2017 A thesis submitted to McGill University in partial fulfillment of the requirements for the degree of Master of Arts. © 2017 Lap Ian Lou i Abstract This study examines the effect of timbre memory decay on the perception of timbre dissimilarity in tones equalized in pitch, loudness and duration. This study makes two hypotheses: (1) the perception of timbre dissimilarity changes as retention interval (RI) increases; (2) timbre familiarity minimizes the perceptual change of timbre dissimilarity with increasing RI. Two experiments were conducted to test these hypotheses. In the first experiment, participants rated the dissimilarity of synthetic tone pairs with RIs of 0.5 s, 5 s and 10 s. In the second experiment, participants rated the dissimilarity of pairs of synthetic tones, digital transformations of acoustic sounds or acoustic instrument sounds with five RIs between 0.5 s and 5 s. The results of the two experiments show that participants perceive similar pairs as significantly more dissimilar as RI increases, particularly for highly unfamiliar synthetic tones, that RI has less of an effect on more dissimilar pairs, and that timbre familiarity minimizes the RI effect on dissimilarity ratings. ii Résumé Cette étude examine l’effet du déclin de la mémoire du timbre sur la perception de dissemblance entre timbres pour des sons égalisés en termes de la hauteur, de la sonie et de la durée. Cette étude fait deux hypothèses: (1) la perception de dissemblance du timbre change lorsque l’intervalle de rétention (IR) augmente; (2) le caractère familier de timbre minimise le changement perceptif de dissemblance avec une augmentation de l’IR. -
History of Cognitive Psychological Memory Research
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/333701129 History of Cognitive Psychological Memory Research Chapter · June 2019 DOI: 10.1017/9781108290876 CITATIONS READS 0 3,810 2 authors: Henry Roediger Jeremy K. Yamashiro Washington University in St. Louis University of California, Santa Cruz 331 PUBLICATIONS 33,867 CITATIONS 14 PUBLICATIONS 115 CITATIONS SEE PROFILE SEE PROFILE Some of the authors of this publication are also working on these related projects: Question Order Effects on Quizzes View project Socially Distributed Remembering View project All content following this page was uploaded by Jeremy K. Yamashiro on 17 June 2019. The user has requested enhancement of the downloaded file. HISTORY OF MEMORY RESEARCH 1 History of Psychological Approaches to Studying Memory Henry L. Roediger, III and Jeremy K. Yamashiro Department of Psychological & Brain Sciences Washington University in St. Louis Correspondence to: Henry L. Roediger, III Department of Psychological and Brain Sciences Campus Box 1125 Washington University in St. Louis One Brookings Drive St. Louis, MO 63130-4899 U.S.A. e-mail: [email protected] HISTORY OF MEMORY RESEARCH 2 Introduction Writings about memory date to the earliest written word, and doubtless people wondered about their memories for centuries before they were able to write down their observations. Aristotle and Plato wrote about memory in ways that seem surprisingly modern even today, although of course in the wisdom of hindsight many of their claims are off the mark. For example, Aristotle thought that the heart was the seat of learning, memory, and intelligence and that the brain existed to cool the heart. -

Restitution of Visual Function in Patients with Cerebral Blindness
J Neurol Neurosurg Psychiatry: first published as 10.1136/jnnp.42.4.312 on 1 April 1979. Downloaded from Journal ofNeurology, Neurosurgery, andPsychiatry, 1979, 42, 312-322 Restitution of visual function in patients with cerebral blindness J. ZIHL AND D. VON CRAMON From the Max-Planck-Institut fur Psychiatrie, Miinchen, Germany SUMMARY Patients with postchiasmatic visual field defects were trained at the border of their visual field. Using a psychophysical method, light-difference thresholds were determined repeatedly in this visual field area. Improvement in contrast sensitivity and increase in size of the visual field could be obtained by this training procedure. The improvement was confined to the trained visual field area and showed interocular transfer indicating its central nature. Although only contrast sensitivity was trained, the observed improvement was not limited to this visual function. Visual acuity, critical flicker fusion, and colour perception also showed an improve- ment suggesting an association of these functions. The improvement was restricted to the training period-no spontaneous recovery was observed between or after the periods of training. It is suggested that a lesion in the central visual system does not always result in a complete and permanent loss of function. The critical level of function that normally has to be reached for a Protected by copyright. sufficient neuronal sensitivity may be obtained by systematic visual stimulation in the area between the intact and blind parts of the visual field. This increase in neuronal sensitivity leads to an improvement in visual performance. Lesions within the central visual pathways do not may be abrupt or gradual (Korner and Teuber, necessarily result in absolute and permanent visual 1973). -

Unusual Spontaneous and Training Induced Visual Field Recovery in A
J Neurol Neurosurg Psychiatry: first published as 10.1136/jnnp.70.2.236 on 1 February 2001. Downloaded from 236 J Neurol Neurosurg Psychiatry 2001;70:236–239 SHORT REPORT Unusual spontaneous and training induced visual field recovery in a patient with a gunshot lesion D A Poggel, E Kasten, E M Müller-Oehring, B A Sabel, S A Brandt Abstract field size could not be ruled out (for example, Over a period of more than 3 years, variability of perimetric measurements, change changes in visual and neuropsychological of detection strategies, or compensatory eccen- functions were examined in a patient with tric fixation) (see also Balliet et al3 for a review). a visual field defect caused by a cerebral However, more recent, methodologically well gunshot lesion. Initially, the patient had controlled studies provided evidence for train- been completely blind, but after 6 months ing induced recovery of visual functions.45 of spontaneous recovery, he showed a Here, we report on a patient with a traumati- homonymous bilateral lower quadran- cally induced visual field defect showing tanopia and impairment of higher visual significant spontaneous recovery and consider- functions. Unexpectedly, recovery still able further progress during visual restitution continued after the first 6 months. This training. For the first time we could show in process was documented in detail by detail that spontaneous as well as training visual field examinations using high reso- induced improvement take place in the area of lution perimetry. When visual field size residual vision and that both processes seem to had stabilised almost 16 months after the be based on a common mechanism—that is, lesion, further improvement could be the modulation of perceptual thresholds in achieved by visual restitution training. -

Colour Vision
Contemporary Physics ISSN: 0010-7514 (Print) 1366-5812 (Online) Journal homepage: https://www.tandfonline.com/loi/tcph20 Colour vision David H. Foster To cite this article: David H. Foster (1984) Colour vision, Contemporary Physics, 25:5, 477-497, DOI: 10.1080/00107518408210723 To link to this article: https://doi.org/10.1080/00107518408210723 Published online: 20 Aug 2006. Submit your article to this journal Article views: 25 Citing articles: 1 View citing articles Full Terms & Conditions of access and use can be found at https://www.tandfonline.com/action/journalInformation?journalCode=tcph20 CONTEMP. PHYS., 1984, VOL. 25, NO. 5, 477497 Colour Vision David H. Foster, Department of Communication and Neuroscience, University of Keele, Keele, Staflordshire ST5 5BG, England ABSTRACT. This article reviews research into human colour vision, most information about which has been derived by psychophysical methods. Thus, the sensitivity of the eye to light of different wavelengths over the spectrum has been accurately estimated for the initial photoreceptor stage which converts light incident on the retina into neural signals. Spectral sensitivities have also been obtained, in part at least, for the subsequent post-receptoral neural pathways that apparently recode colour information into separate signals specifying luminance and chromaticity. These and other findings on receptoral and post-receptoral spectral sensitivities are considered in relation to techniques for functionally isolating colour-processing pathways in the human visual system. Also discussed briefly are models of colour vision, the relationship between form perception and colour vision, and inherited and acquired colour-vision deficiencies. 1. Introduction Research into human colour vision has been strongly influenced by the theoretical approach and experimental methods of psychophysics, this being the study of the quantitative relationship between the physical characteristics of sensory stimuli and the corresponding sensory experience reported by an observer. -
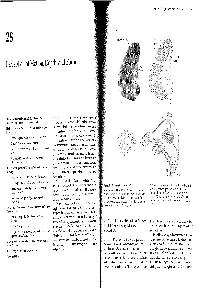
Perception of Motion, Depth, and Form 549
Chapter 28 I Perception of Motion, Depth, and Form 549 A 28 Stripes in area 18 lnterblob Perception of Motion, Depth, and Form Blob V2 V1 B The Parvocellular and Magnocellular Pathways Feed Into N VISION, AS IN OTHER mental operations, we experi- Two Processing Pathways in Extrastriate Cortex ence the world as a whole. Independent attributes- depth, form, and color-are coordinated Motion Is Analyzed Primarily in the Dorsal Pathway to the I motion, Parietal Cortex into a single visual image. In the two previous chapters Motion Is Represented in the Middle Temporal Area we began to consider how two parallel pathways-the magnocellular and parvocellular pathways, that extend Cells in MT Solve the Aperture Problem from the retina through the lateral geniculate nucleus of Control of Movement Is Selectively Impaired by Lesions the thalamus to the primary visual (striate) cortex- ofMT might produce a coherent visual image. In this chapter Perception of Motion Is Altered by Lesions and we examine how the information from these two path- Microstimulation of MT ways feeds into multiple higher-order centers of visual Depth Vision Depends on Monocular Cues and Binocular processing in the extrastriate cortex. How do these path- Disparity ways contribute to our perception of motion, depth, Monocular Cues Create Far-Field Depth Perception form, and color? The magnocellular (M) and parvocellular (P) path- Stereoscopic Cues Create Near-Field Depth Perception ways feed into two extrastriate cortical pathways: a dor- Figure 28-1 Organization of V1 and V2. B. Connections between V1 and V2. The blobs in V1 connect Information From the Two Eyes Is First Combined in the sal pathway and a ventral pathway. -

Shape and Color in Image Recognition
UNIVERSITY OF LATVIA FACULTY OF PHYSICS AND MATHEMATICS Sergejs Fomins SHAPE AND COLOR IN IMAGE RECOGNITION Summary of the Doctoral Thesis Promotion to the Degree of Doctor of Physics Subbranch: Medical Physics Rīga, 2011 Thesis was developed in the period from 2006 to 2011 at the Faculty of Physics and Mathematics of the University of Latvia Scientific advisor: Dr. habil. phys., Prof. Māris Ozoliņš Reviewers: Dr. habil. phys., Prof. Jānis Spīgulis, Institute of Atomic Physics and Spectroscopy, University of Latvia Dr. phys. Jānis Teteris, Institute of Solid State Physics, University of Latvia Prof. Henrikas Vaitkevicius, Vilnius University The defense of the PhD thesis will take place in an open session of the Promotion Council of Medicine Physics on 11th of February, 2011, at 15:00 in the conference hall of the Institute of Solid State Physics of University of Latvia. Chairperson of the Specialized Promotion Council of the scientific section of Physics and Astronomy at the University of Latvia: Dr. habil. phys., Prof. Ivars Lācis The PhD Thesis and its summary are available at the Library of the University of Latvia (4 Kalpaka Blvd, Rīga), Latvian Academic Library (10 Rūpniecības Str.), and at the Faculty of Physics and Mathematics of the University of Latvia (room F210). © Sergejs Fomins, 2011 © University of Latvia, 2011 ISBN 978-9984-45-304-0 CONTENts Abstract ....................................................................................................................................... 4 Introduction ..............................................................................................................................