An Ultra-Thin Multiband Terahertz Metamaterial Absorber and Sensing Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Conference Schedule
ICBBS 2019 CONFERENCE ABSTRACT CONFERENCE ABSTRACT 2019 8th International Conference on Bioinformatics and Biomedical Science (ICBBS 2019) October 23-25, 2019 Grand Gongda Jianguo Hotel, Beijing, China Organized by Co-organized by Published and Indexed by http://www.icbbs.org/ ICBBS 2019 CONFERENCE ABSTRACT ICBBS 2019 CONFERENCE ABSTRACT Table of Contents Introduction 4 Conference Committee 5~6 Program at-a-Glance 7~9 Presentation Instruction 10 Keynote Speaker Introduction 11~19 Invited Speaker Introduction 20~21 Oral Session on October 24, 2019 Session 1: Feature Extraction and Image Segmentation 22~26 Session 2: Pattern Recognition and Image Classification 27~31 Session 3: Medical Image Processing and Medical Testing 32~37 Session 4: Data Analysis and Soft Computing 38~42 Session 5: Target Detection 43~47 Session 6: Image Analysis and Signal Processing 48~53 Session 7: Molecular Biology and Biomedicine 54~59 Session 8: Computer Information Technology and Application 60~64 Poster Session on October 25, 2019 65~84 Conference Venue 85~86 Note 87~88 ICBBS 2019 CONFERENCE ABSTRACT Introduction Welcome to 2019 8th International Conference on Bioinformatics and Biomedical Science (ICBBS 2019) which is organized by Beijing University of Technology and Biology and Bioinformatics (BBS) under Hong Kong Chemical, Biological & Environmental Engineering Society (CBEES), co-organized by Tiangong University and Hebei University of Technology. The objective of ICBBS 2019 is to provide a platform for researchers, engineers, academicians as well as industrial professionals from all over the world to present their research results and development activities in Bioinformatics and Biomedical Science. Papers will be published in the following proceedings: ACM Conference Proceedings (ISBN: 978-1-4503-7251-0): archived in ACM Digital Library, indexed by EI Compendex and SCOPUS, and submitted to be reviewed by Thomson Reuters Conference Proceedings Citation Index (ISI Web of Science). -

University of Leeds Chinese Accepted Institution List 2021
University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams. -

Proper Pesticide Application in Agricultural Products €
Food Control 122 (2021) 107788 Contents lists available at ScienceDirect Food Control journal homepage: www.elsevier.com/locate/foodcont Review Factors influencing Chinese farmers’ proper pesticide application in agricultural products – A review Yingxuan Pan a,1, Yingxue Ren b,1, Pieternel A. Luning a,* a Food Quality and Design, Department of Agrotechnology and Food Sciences, Wageningen University, P.O. Box 17, 6700 AA, Wageningen, the Netherlands b Management Science, School of Economics and Management, TianGong University, 300387, Tianjin, PR China ARTICLE INFO ABSTRACT Keywords: Pesticide residues in agricultural products are a persistent food safety issue in China. The current review aims to Chinese farmers get a comprehensive understanding of factors influencing farmers’ proper pesticide application in China. To Pesticide application achieve that, the study developed an analytical framework based on the principles of the Theory of Planned Theory of Planned Behaviour Behaviour (TPB) and the techno-managerial approach. Following the framework, the study conducted a semi- Techno-managerial approach structured literature review and yielded multiple factors related to farmers (i.e. their characteristics and TPB Interventions elements), external circumstances (i.e. governmental supervision, the roles of suppliers and the support of extension services) and technological conditions (i.e. equipment and environmental conditions), which can in fluence pesticide application of farmers. To improve farmers’ behaviour, a stepwise approach of interventions targeted to different actors was proposed. Future research on the effectiveness of the application of the stepwise interventions on pesticide use is suggested. 1. Introduction like toxic cowpeas in southern China (Huan, Xu, Luo, & Xie, 2016). Several studies indicated that pesticide residues relate to the Pesticides are widely used against pest in agricultural production behaviour of farmers, specifically their pesticide application (Jallow, (WHO, 2017). -
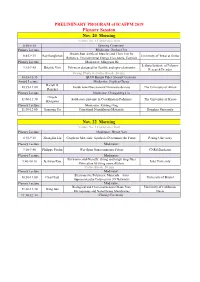
2019ICAFPM-PRELIMINARY PROGRAM-07112019.Xlsx
PRELIMINARY PROGRAM of ICAFPM 2019 Plenary Session Nov. 20 Morning Venue: No. 1 Conference Hall 8:30-8:45 Opening Ceremony Plenary Lecture Moderator: Junhao Chu Sheath-Run Artificial Muscles and Their Use for 8:45-9:15 Ray Baughman University of Texas at Dallas Robotics, Environmental Energy Harvesters, Comfort Plenary Lecture Moderator: Mingyuan He Leibniz Institute of Polymer 9:15-9:45 Brigitte Voit Polymers designed for flexible and opto-electronics Research Dresden Group Photo & Coffee Break 20 min 10:05-10:35 QIAN Baojun Fiber Award Ceremony Award Lecture Moderator: Stephen Cheng Darrell H. 10:35-11:00 Inside nanofibers toward Nanoware devices The University of Akron Reneker Plenary Lecture Moderator: Changsheng Liu Hiroshi 11:00-11:30 Solid-state protonic in Coordination Polymers The University of Kyoto Kitagawa Plenary Lecture Moderator: Kuiling Ding 11:30-12:00 Jianyong Yu Functional Nanofibrous Materials Donghua University Nov. 22 Morning Venue: No. 1 Conference Hall Plenary Lecture Moderator: Deyue Yan 8:30-9:10 Zhongfan Liu Graphene Materials: Synthesis Determines the Future Peking University Plenary Lecture Moderator: 9:10-9:40 Philippe Poulin Wet-Spun Nanocomposite Fibers CNRS Bordeaux Plenary Lecture Moderator: Environmental-friendly, strong and tough long-fiber 9:40-10:10 Jaehwan Kim Inha University fabrication by using nanocellulose Coffee Break 20 min Plenary Lecture Moderator: Electroactive Polymeric Materials – from 10:30-11:00 Charl Faul University of Bristol Supramolecular Polymers to 3D Networks Plenary Lecture Moderator: Biological and Chemical Sensors Made from University of California, 11:00-11:30 Gang Sun Microporous and Nanofibrous Membranes Davis 11:30-12:00 Closing Ceremony PRELIMINARY PROGRAM of ICAFPM 2019 Parallel Session Nov. -

Conference Program
CONFERENCE PROGRAM 2020 6th International Conference on Computing and Artificial Intelligence (ICCAI 2020) & 2020 2nd International Conference on Intelligent Medicine and Image Processing (IMIP 2020) April 23-26, 2020|Tianjin, China Organized by Supported by Gold Sponsor Table of Contents 1. Welcome Letter 3 2. Presentation Guideline 4 3. ZOOM User Guideline 6 4. Program-at-a-Glance 7 4.1 Test Session Schedule 7 4.2 Formal Session Schedule 8 5. Keynote Speaker 10 6. Invited Speaker 14 7. Detailed Program for Poster Session 17 7.1 Poster Session 1--Topic: “Computer Vision and Image Processing Technology” 17 7.2 Poster Session 2--Topic: “Modern Information Theory and Applied Technology” 19 8. Detailed Program for Oral Session 21 8.1 Oral Session 1--Topic: “Machine Learning and Intelligent Computing” 21 8.2 Oral Session 2--Topic: “Next-generation Neural Network and Applications” 22 8.3 Oral Session 3--Topic: “Data Analysis and Processing” 23 8.4 Oral Session 4--Topic: “Big Data Science and Information Intelligence” 24 8.5 Oral Session 5--Topic: “Target Detection” 25 8.6 Oral Session 6--Topic: “Image Transformation and Calculation” 26 8.7 Oral Session 7--Topic: “Intelligent Identification and Control Technology” 27 8.8 Oral Session 8--Topic: “Medical Image Analysis and Processing” 28 8.9 Oral Session 9--Topic: “Computer Network and Information Communication System” 29 8.10 Oral Session 10--Topic: “Computer and Information Science” 30 9. About ICCAI 2021&IMIP 2021 31 2 Welcome Letter Dear distinguished delegates, On behalf of the organizing committee, I would like to express my sincere thanks to all of you for participating in 2020 6th International Conference on Computing and Artificial Intelligence (ICCAI 2020) and 2020 2nd International Conference on Intelligent Medicine and Image Processing (IMIP 2020) which will be held during April 23-26, 2020. -

EDTA for Adsorptive Removal of Sulfamethoxazole
Desalination and Water Treatment 207 (2020) 321–331 www.deswater.com December doi: 10.5004/dwt.2020.26391 Magnetic porous Fe–C materials prepared by one-step pyrolyzation of NaFe(III)EDTA for adsorptive removal of sulfamethoxazole Jiandong Zhua,†, Liang Wanga,†, Yawei Shia,*, Bofeng Zhangb, Yajie Tianc, Zhaohui Zhanga, Bin Zhaoa, Guozhu Liub,*, Hongwei Zhanga,d aState Key Laboratory of Separation Membranes and Membrane Processes, School of Environmental Science and Engineering, Tiangong University, Tianjin 300387, China, Tel./Fax: +86 22 83955392; emails: [email protected] (Y.W. Shi), [email protected] (J.D. Zhu), [email protected] (L. Wang), [email protected] (Z.H. Zhang), [email protected] (B. Zhao), [email protected] (H.W. Zhang) bSchool of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China, Tel. +86 22 27892340; emails: [email protected] (G.Z. Liu), [email protected] (B.F. Zhang) cHenan Engineering Research Center of Resource & Energy Recovery from Waste, College of Chemistry and Chemical Engineering, Henan University, Kaifeng 475004, China, email: [email protected] (Y.J. Tian) dSchool of Environmental Science and Engineering, Tianjin University, Tianjin 300072, China Received 25 February 2020; Accepted 25 July 2020 abstract A series of magnetic porous Fe–C materials were prepared by one-step pyrolyzation of ethylene- diaminetetraacetic acid sodium iron(III) at 500°C–800°C and then employed as adsorbents for sulfamethoxazole (SMX) adsorption. The one prepared at 700°C (Fe–C-700) was selected as the opti- mum one with an adsorption amount of 82.3 mg g–1 at pH 5.0 and 30°C. -

Shoreline Changes Along the Coast of Mainland China—Time to Pause and Reflect?
International Journal of Geo-Information Article Shoreline Changes Along the Coast of Mainland China—Time to Pause and Reflect? Hongzhen Tian 1,* , Kai Xu 1, Joaquim I. Goes 2, Qinping Liu 1, Helga do Rosario Gomes 2 and Mengmeng Yang 3 1 School of Economics and Management, Tiangong University, Tianjin 300387, China; [email protected] (K.X.); [email protected] (Q.L.) 2 Lamont Doherty Earth Observatory, Columbia University, New York, NY 10964, USA; [email protected] (J.I.G.); [email protected] (H.d.R.G.) 3 Institute for Space-Earth Environmental Research (ISEE), Nagoya University, Nagoya 464-8601, Japan; [email protected] * Correspondence: [email protected] Received: 19 August 2020; Accepted: 28 September 2020; Published: 29 September 2020 Abstract: Shoreline changes are of great importance for evaluating the interaction between humans and ecosystems in coastal areas. They serve as a useful metric for assessing the ecological costs of socioeconomic developmental activities along the coast. In this paper, we present an assessment of shoreline changes along the eastern coast of mainland China from ~1990 to 2019 by applying a novel method recently developed by us. This method which we call the Nearest Distance Method (NDM) is used to make a detailed assessment of shorelines delineated from Landsat Thematic Mapper (TM) and Operational Land Imager (OLI) images. The results indicate a dramatic decline in natural shorelines that correspond to the rapid increase in the construction of artificial shorelines, driven by China’s economic growth. Of the entire coast of mainland China, the biggest change occurred along the Bohai Sea, where artificial shorelines expanded from 42.4% in ~1990 to 81.5% in 2019. -
F786bd961.Pdf
Conference Program ZJU-UIUC INSTITUTE 2 Map of Deefly Zhejiang Hotel Address: Deefly Zhejiang Hotel, 278 Santaishan Road, Xihu District, Hangzhou 地址:杭州市西湖区三台山路 278 号 浙江宾馆 3 Map of VIP Building Map of Main Building 4 IEEE MTT-S NEMO 2020 Co-Organizers Zhejiang University Shanghai Jiaotong University Beijing Jiaotong University Beihang University Xidian University Tianjin University Anhui University Ningbo University Tsinghua University Xi’an Jiaotong University Nanjing University of Science & Technology Fudan University University of Electronic Science and Technology of China Hangzhou Dianzi University Jimei University Jiangsu University of Science and Technology Shenzhen University CEPREI National Key Laboratory on Electromagnetic Environment Effects Shanghai Key Laboratory of Electromagnetic Environmental Effects for Aerospace Vehicle IEEE MTT-S NEMO 2020 Sponsors MTT-S Zhaolong Cables & Interconnects Xpeedic Technology, Inc General Test Systems Inc. Cloud-Promise Co., Ltd WIPL-D d.o.o. Co., Ltd APS 5 Table of Contents Greetings from IEEE MTT-S NEMO 2020 General Co-Chairs ............................... 9 NEMO2020 Committee Officers ............................................................................ 10 NEMO2020 TPC Members ..................................................................................... 17 Conference Site and Office Location ................................................................... 20 General Information ............................................................................................. -
Artificial Intelligence-Enabled ECG Algorithm Based on Improved Residual Network for Wearable
sensors Article Artificial Intelligence-Enabled ECG Algorithm Based on Improved Residual Network for Wearable ECG Hongqiang Li 1,* , Zhixuan An 1 , Shasha Zuo 2, Wei Zhu 2, Zhen Zhang 3, Shanshan Zhang 1,4, Cheng Zhang 1, Wenchao Song 1, Quanhua Mao 1, Yuxin Mu 1, Enbang Li 5 and Juan Daniel Prades García 6 1 Tianjin Key Laboratory of Optoelectronic Detection Technology and Systems, School of Electrical and Electronic Engineering, Tiangong University, Tianjin 300387, China; [email protected] (Z.A.); [email protected] (S.Z.); [email protected] (C.Z.); [email protected] (W.S.); [email protected] (Q.M.); [email protected] (Y.M.) 2 Textile Fiber Inspection Center, Tianjin Product Quality Inspection Technology Research Institute, Tianjin 300192, China; [email protected] (S.Z.); [email protected] (W.Z.) 3 School of Computer Science and Technology, Tiangong University, Tianjin 300387, China; [email protected] 4 Tianjin Key Laboratory of Optoelectronic Sensor and Sensing Network Technology, Institute of Modern Optics, Nankai University, Tianjin 300071, China 5 Centre for Medical Radiation Physics, University of Wollongong, Wollongong, NSW 2522, Australia; [email protected] 6 Institute of Nanoscience and Nanotechnology (IN2UB), Universitat de Barcelona (UB), E-08028 Barcelona, Spain; [email protected] * Correspondence: [email protected] Abstract: Heart disease is the leading cause of death for men and women globally. The residual Citation: Li, H.; An, Z.; Zuo, S.; network (ResNet) evolution of electrocardiogram (ECG) technology has contributed to our under- Zhu, W.; Zhang, Z.; Zhang, S.; standing of cardiac physiology. We propose an artificial intelligence-enabled ECG algorithm based Zhang, C.; Song, W.; Mao, Q.; Mu, Y.; on an improved ResNet for a wearable ECG. -

2019 China-Australia Civil, Materials and Environment Forum PROGRAM
2019 China-Australia Civil, Materials and Environment Forum PROGRAM 27-29th December, Tianjin, China Welcome to CAF2019 Dear friends and colleagues: We are pleased to announce that 2019 China-Australia Civil, Materials and Environment Forum (CAF2019) will be held on December 27-29th, 2019 in Tianjin, China. The conference will be hosted by Hebei University of Technology (HEBUT) and Federation of Chinese Scholars in Australia (FOCSA). There are already profound research collaboration and academic connections between China and Australia. The aim of this forum is to bring together experts, scholars, industry practitioners and policy makers in areas of Civil, Materials and Environment from China and Australia to have in-depth discussions on hot issues related to these areas, exchange ideas and experiences, enhance the existing links and identify new opportunities for collaboration. We believe that these interactions and networking opportunities will further foster and deepen the collaborations in science, technology and higher education between China and Australia. The forum will promote the applications of scientific and technological innovations in related fields in the coordinated development of Beijing-Tianjin-Hebei and the construction of Xiong'an New District. We warmly welcome you to come to the CAF2019 and look forward to seeing you in Tianjin! Sincerely, Prof. Guowei Ma, Vice-president Heibei Universigy of Technology (HEBUT), China Prof. Zhiguo Yuan, AM, FTSE The University of Queensland (UQ), Australia 1 Introduction Hebei University of Technology (HEBUT) is a key university as well as one of the national universities under "Project 211". Situated in Tianjin city, it is also an important co-construction university under the authority of Hebei Province, Tianjin City and China Ministry of Education. -

2020 MCM Problem a Contest Results
2020 Mathematical Contest in Modeling® Press Release—April 24, 2020 COMAP is pleased to announce the results of the 36th annual real possibility that these companies might have to relocate their Mathematical Contest in Modeling (MCM). This year, 13753 teams fishing base in order to continue operations. This created a situation representing institutions from twenty countries/regions participated in uniquely apart from large scale commercial operations capable of the contest. Nineteen teams from the following institutions were pursuing the two species wherever they may go. Teams were also designated as OUTSTANDING WINNERS: asked to address implications if the species relocated into new national boundary waters, an action that could have fishing companies running Beijing Institute of Technology, China afoul of established political agreements. With the U.K. poised to exit Beijing Normal University, China (Frank Giordano Award) the European Union at the time this problem was created, the A Dongbei University of Finance and Economics, China problem placed teams within a subset of very real implications of this (ASA Data Insights Award) move on the Scottish small scale fishing industry. Harbin Institute of Technology, China AMS Award NC School of Science and Mathematics, NC, USA The B problem asked a common question of children of all ages: what (SIAM Award & MAA Award) is the best geometric shape to use as a sandcastle foundation in the face North University of China, China, (SIAM Award & AMS Award) of tides and surf? Conditions restricted the problem setting to one Northeast Electric Power University, China supporting a cross-comparison of shapes, sizes, and designs based on Northwestern Polytechnical University, China measures of ‘best’ that teams developed. -
A Robust Sleep Apnea-Hypopnea Syndrome Automated Detection Method Based on Fuzzy Entropy Using Single Lead-EEG Signals
A Robust Sleep Apnea-hypopnea Syndrome Automated Detection Method Based on Fuzzy Entropy Using Single Lead-EEG Signals Yao Wang Department of Biomedical Engineering, School of Life Sciences, Tiangong University, Tianjin, 300387 Tianshun Yang School of Electrical and Electronic Engineering, Tiangong University, Tianjin, 300387 Siyu Ji School of Electrical and Electronic Engineering, Tiangong University, Tianjin, 300387 Xiaohong Wang Department of Biomedical Engineering, School of Life Sciences, Tiangong University, Tianjin, 300387 Huiquan Wang Department of Biomedical Engineering, School of Life Sciences, Tiangong University, Tianjin, 300387 Jinhai Wang Department of Biomedical Engineering, School of Life Sciences, Tiangong University, Tianjin, 300387 Xiaoyun Zhao ( [email protected] ) Department of Respiratory and Critical Care Medicine & Sleep Center, Tianjin Chest Hospital, Tianjin, 300222 Research Article Keywords: machine learning, sleep apnea/hypopnea, fuzzy entropy, EEG signals, automated detection Posted Date: June 1st, 2021 DOI: https://doi.org/10.21203/rs.3.rs-558448/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License A robust sleep apnea-hypopnea syndrome automated detection method based on fuzzy entropy using single lead-EEG signals Yao Wang a, b,c, Tianshun Yangb, Siyu Jib, Xiaohong Wanga, Huiquan Wanga, Jinhai Wanga and Xiaoyun Zhaod,* a. Department of Biomedical Engineering, School of Life Sciences, Tiangong University, Tianjin, 300387, China; b. School of