DOCSLIB.ORG

Tools for Discovering and Characterizing Extrasolar Planets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Tools for Discovering and Characterizing Extrasolar Planets Tools for discovering and characterizing extrasolar planets PhD Dissertation Written by: Andr´as P´al Lorand´ Eotv¨ os¨ University, Faculty of Sciences PhD School of Physics PhD Program of Particle- and Astrophysics Head of PhD School of Physics: Prof. Zal´an Horv´ath Head of the PhD program: Prof. Ferenc Csikor Thesis advisor: Dr. G´asp´ar Bakos, postdoctoral fellow of the National Science Foundation Harvard-Smithsonian Center for Astrophysics Supervisor: Prof. B´alint Erdi,´ professor Department of Astronomy Lor´and E¨otv¨os University Lor´and E¨otv¨os University Budapest, Hungary 2009 Foreword Among the group of extrasolar planets, transiting planets provide a great opportunity to obtain direct measurements for the basic physical properties, such as mass and radius of these objects. These planets are therefore highly important in the understanding of the evolution and formation of planetary systems: from the observations of photometric transits, the interior structure of the planet and atmospheric properties can also be constrained. The most efficient way to search for transiting extrasolar planets is based on wide-field surveys by hunting for short and shallow periodic dips in light curves covering quite long time intervals. These surveys monitor fields with several degrees in diameter and tens or hundreds of thousands of objects simultaneously. In the practice of astronomical observations, surveys of large field-of-view are rather new and therefore require special methods for photometric data reduction that have not been used before. Since 2004, I participate in the HATNet project, one of the leading initiatives in the competitive search for transiting planets. Due to the lack of software solution which is capable to handle and properly reduce the yield of such a wide-field survey, I have started to develop a new package designed to perform the related data processing and analysis. After several years of improvement, the software package became sufficiently robust and played a key role in the discovery of several transiting planets. In addition, various new algorithms for data reduction had to be developed, implemented and tested which were relevant during the reduction and the interpretation of data. In this PhD thesis, I summarize my efforts related to the development of a complete software solution for high precision photometric reduction of astronomical images. I also demonstrate the role of this newly developed package and the related algorithms in the case of particular discoveries of the HATNet project. i ii Contents 1 Introduction 1 2 Algorithms and Software environment 5 2.1 Difficulties with undersampled, crowded and wide-field images ........ 6 2.1.1 Undersampledimages........................... 7 2.1.2 Crowdedimages.............................. 12 2.1.3 Largefield-of-view ............................ 13 2.2 Problems with available software solutions . ......... 16 2.3 Calibrationandmasking . .. 16 2.3.1 Stepsofthecalibrationprocess . ... 17 2.3.2 Masking .................................. 18 2.3.3 Implementation .............................. 19 2.4 Detectionofstars................................ 21 2.4.1 Imagepartitioning ............................ 23 2.4.2 Coordinates, shape parameters and analytic models . ........ 27 2.4.3 Implementation .............................. 31 2.5 Astrometry .................................... 31 2.5.1 Introduction................................ 31 2.5.2 Symmetricpointmatching . 33 2.5.3 Findingthetransformation. .. 34 2.5.4 Implementation .............................. 42 2.6 Registeringimages ............................... 43 2.6.1 Choosingareferenceimage . 44 2.6.2 Relativetransformations . .. 44 2.6.3 Conservingflux .............................. 46 2.6.4 Implementation .............................. 47 iii 2.7 Photometry .................................... 48 2.7.1 Rawinstrumentalmagnitudes . 48 2.7.2 Formalismfortheaperturephotometry . .... 50 2.7.3 Magnitudetransformations. .. 51 2.7.4 Implementation .............................. 52 2.8 Imageconvolutionandsubtraction . ..... 52 2.8.1 Referenceframe.............................. 55 2.8.2 Registration................................ 55 2.8.3 Implementation .............................. 56 2.9 Photometryonsubtractedimages . .... 56 2.10Trendfiltering.................................. 57 2.10.1 BasicequationsfortheEPDandTFA . 60 2.10.2 Reconstructive and simultaneous trend removals . ......... 61 2.10.3 Efficiencyofthesemethods . 63 2.11 Majorconcepts ofthesoftwarepackage . ....... 63 2.11.1 Datastructures .............................. 65 2.11.2 Operatingenvironment . 66 2.12Implementation ................................. 68 2.12.1 Basic operations on FITS headers and keywords – fiheader ..... 70 2.12.2 Basic arithmetic operations on images – fiarith ........... 71 2.12.3 Basic information about images – fiinfo ................ 72 2.12.4 Combination of images – ficombine .................. 72 2.12.5 Calibration of images – ficalib ..................... 73 2.12.6 Rejection and masking of nasty pixels – fiign ............. 73 2.12.7 Generation of artificial images – firandom ............... 74 2.12.8 Detection of stars or point-like sources – fistar ............ 76 2.12.9 Basic coordinate list manipulations – grtrans ............. 76 2.12.10 Matching lists or catalogues – grmatch ................. 77 2.12.11 Transforming and registering images – fitrans ............ 78 2.12.12 Convolution and image subtraction – ficonv .............. 79 2.12.13 Photometry – fiphot ........................... 80 2.12.14 Transposition of tabulated data – grcollect .............. 81 2.12.15 Archiving – fizip and fiunzip ..................... 84 2.12.16 Generic arithmetic evaluation, regression and data analysis – lfit .. 85 iv 2.13 Analysisofphotometricdata. ..... 88 3 HATNet discoveries 93 3.1 Photometricdetection . .. .. .. 93 3.2 Follow-upobservations . ... 97 3.2.1 Reconnaissance spectroscopy . ... 97 3.2.2 Highresolutionspectroscopy. ... 97 3.2.3 Photometric follow-up observations . ..... 98 3.2.4 Excluding blend scenarios . 99 3.3 Analysis ...................................... 100 3.3.1 Independentfits.............................. 101 3.3.2 Joint fit based on the aperture photometry data and the single partial follow-uplightcurve . 105 3.3.3 Joint fit based on the image subtraction photometry data and both of thefollow-uplightcurves. 106 3.3.4 Stellarparameters ............................ 108 3.3.5 Planetaryandorbitalparameters . 109 4 Follow-up observations 111 4.1 Photometric observations and reductions . ........ 112 4.2 Radialvelocityobservations . ..... 115 4.3 An analytical formalism for Kepler’s problem . ......... 116 4.3.1 Mathematicalformalism . 116 4.3.2 Additional constraints given by the transits . ....... 119 4.3.3 Practicalimplementation. 120 4.4 Analysis of the HAT-P-2 planetary system . ...... 121 4.4.1 Light curve and radial velocity parameters . ...... 122 4.4.2 Effects of the orbital eccentricity . .... 123 4.4.3 Jointfit .................................. 125 4.4.4 Stellarparameters ............................ 126 4.4.5 Planetaryparameters. 127 4.4.6 Photometric parameters and the distance of the system ........ 128 4.5 Discussion..................................... 130 5 Summary 133 v vi Chapter 1 Introduction In the last two decades, the discovery and characterization of extrasolar planets became an exciting field of astronomy. The first companion that was thought to be an object roughly 10 times more massive than Earth, had been detected around the pulsar PSR1829-10 (Bailes, Lyne & Shemar, 1991). Although this detection turned out to be a false one (Lyne & Bailes, 1992), shortly after the method of detecting planetary companions involving the analysis of pulsar timing variations led to the successful confirmation of the multiple planetary sys- tem around PSR1257+12 (Wolszczan & Frail, 1992). The pioneering discovery of a planet orbiting a main sequence star was announced by Mayor & Queloz (1995). They reported the presence of a short-period planet orbiting the Sun-like star 51 Peg. This detection was based on precise radial velocity measurements with uncertainties at the level of meter per second. Both discovery methods mentioned above are based on the fact that all components in a single or multiple planetary system, including the host star itself, revolve around the common barycenter, that is the point in the system having inertial motion. Thus, com- panions with smaller masses offset the barycenter only slightly from the host star whose motion is detected, either by the analysis of pulsar timing variations or by radial velocity measurements. Therefore, such methods – which are otherwise fairly common among the investigation techniques of binary or multiple stellar systems – yielded success in the form of confirming planets only after the evolution of instrumentation. Due to the physical con- straints found in these methods, the masses of the planets can only be constrained by a lower limit, while we even do not have any information on the sizes of these objects. The discovery of 51 Peg b was followed by numerous other detections, mainly by the method of radial velocity analysis, yielding the discovery, for instance, of the first planetary system with two planets around 47 UMa (Butler & Marcy, 1996; Fischer et al., 2002), and the first multiple planetary system around υ And (Butler et al., 1999). Until the first photometric detection of planetary transits in the system of HD 209458(b) (Henry et al., 2000; Charbonneau et
Load more

Recommended publications
  • Arxiv:Astro-Ph/0609369 V2 15 Sep 2006 Ahntnd,54 Ra Rnhr.N,Wsigo DC, Washington NW, Rd
    Draft version September 18, 2006 – VERSION Accepted for publication in ApJ A Preprint typeset using LTEX style emulateapj v. 12/14/05 HAT-P-1b: A LARGE-RADIUS, LOW-DENSITY EXOPLANET TRANSITING ONE MEMBER OF A STELLAR BINARY† ⋆ G. A.´ Bakos1,2, R. W. Noyes1, G. Kovacs´ 3, D. W. Latham1, D. D. Sasselov1, G. Torres1, D. A. Fischer6, R. P. Stefanik1, B. Sato7, J. A. Johnson8, A. Pal´ 4,1, G. W. Marcy8, R. P. Butler9, G. A. Esquerdo1, K. Z. Stanek10, J. Laz´ ar´ 5, I. Papp5, P. Sari´ 5 & B. Sipocz˝ 4,1 Draft version September 18, 2006 – VERSION Accepted for publication in ApJ ABSTRACT Using small automated telescopes in Arizona and Hawaii, the HATNet project has detected an object transiting one member of the double star system ADS 16402. This system is a pair of G0 main-sequence stars with age about 3 Gyr at a distance of ∼139 pc and projected separation of ∼1550 AU. The transit signal has a period of 4.46529 days and depth of 0.015 mag. From follow-up photometry and spectroscopy, we find that the object is a “hot Jupiter” planet with mass about 0.53 MJ and radius ∼1.36 RJ traveling in an orbit with semimajor axis 0.055 AU and inclination about 85◦.9, thus transiting the star at impact parameter 0.74 of the stellar radius. Based on a data set spanning three years, ephemerides for the transit center are: TC = 2453984.397+ Ntr ∗ 4.46529. The planet, designated HAT-P-1b, appears to be at least as large in radius, and smaller in mean density, than any previously-known planet.
    [Show full text]
  • Exoplanet Detection Techniques
    Exoplanet Detection Techniques Debra A. Fischer1, Andrew W. Howard2, Greg P. Laughlin3, Bruce Macintosh4, Suvrath Mahadevan5;6, Johannes Sahlmann7, Jennifer C. Yee8 We are still in the early days of exoplanet discovery. Astronomers are beginning to model the atmospheres and interiors of exoplanets and have developed a deeper understanding of processes of planet formation and evolution. However, we have yet to map out the full complexity of multi-planet architectures or to detect Earth analogues around nearby stars. Reaching these ambitious goals will require further improvements in instru- mentation and new analysis tools. In this chapter, we provide an overview of five observational techniques that are currently employed in the detection of exoplanets: optical and IR Doppler measurements, transit pho- tometry, direct imaging, microlensing, and astrometry. We provide a basic description of how each of these techniques works and discuss forefront developments that will result in new discoveries. We also highlight the observational limitations and synergies of each method and their connections to future space missions. Subject headings: 1. Introduction tary; in practice, they are not generally applied to the same sample of stars, so our detection of exoplanet architectures Humans have long wondered whether other solar sys- has been piecemeal. The explored parameter space of ex- tems exist around the billions of stars in our galaxy. In the oplanet systems is a patchwork quilt that still has several past two decades, we have progressed from a sample of one missing squares. to a collection of hundreds of exoplanetary systems. Instead of an orderly solar nebula model, we now realize that chaos 2.
    [Show full text]
  • X. Huang, G. Á. Bakos and J. A. Hartman [email protected]
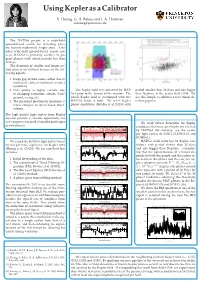
    Using Kepler as a Calibrator X. Huang, G. Á. Bakos and J. A. Hartman [email protected] PROBLEM OBSERVATION The HATNet project is a wide-field ground-based search for transiting plan- ets around moderately bright stars. Like other wide-field ground-based transit sur- veys, HATNet is primarily sensitive to gas giant planets with orbital periods less than 10 days. The detection of smaller and longer pe- riod planets are difficult because of the fol- lowing aspects. 1. Large gap in time series, either due to rotation of earth, or inclement weather conditions. 2. Data quality is highly variable due The Kepler field was observed by HAT- period smaller than 20 days and size bigger to changing extinction, clouds, back- Net prior to the launch of the mission. The than Neptune in the center field G154. We ground, seeing, etc. whole Kepler field is overlapped with five use this sample to calibrate a new transit de- 3. The per-point photometry precision is HATNet fields in total. We select Kepler tection pipeline. worse compare to space based obser- planet candidates (Batalha et al.(2013)) with vations. The high quality light curves from Kepler mission provide a valuable opportunity for EXAMPLE HAT LIGHT CURVES RESULT us to improve our yield of smaller and longer We yield robust detections for Kepler period planets. -0.01 HAT1998264, unbinned candidates that were previously not selected HAT1998264, binned average -0.005 KOI12.01, binned average by HATNet (for instance, see the exam- 0 mag ple light curves of KOI12.01,KOI18.01 and METHOD 6 0.005 0.01 KOI98.01).
    [Show full text]
  • A Global Network of Fully Automated Identical Wide-Field Telescopes Author(S): G
    HATSouth: A Global Network of Fully Automated Identical Wide-Field Telescopes Author(s): G. Á. Bakos, Z. Csubry, K. Penev, D. Bayliss, A. Jordán, C. Afonso, J. D. Hartman, T. Henning, G. Kovács, R. W. Noyes, B. Béky, V. Suc, B. Csák, M. Rabus, J. Lázár, I. Papp, P. Sári, P. Conroy, G. Zhou, P. D. Sackett, B. Schmidt, L. Mancini, D. D. Sasselov, and K. Ueltzhoeffer Source: Publications of the Astronomical Society of the Pacific, Vol. 125, No. 924 (February 2013), pp. 154-182 Published by: The University of Chicago Press on behalf of the Astronomical Society of the Pacific Stable URL: http://www.jstor.org/stable/10.1086/669529 . Accessed: 22/01/2014 07:46 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp . JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. The University of Chicago Press and Astronomical Society of the Pacific are collaborating with JSTOR to digitize, preserve and extend access to Publications of the Astronomical Society of the Pacific. http://www.jstor.org This content downloaded from 200.89.68.74 on Wed, 22 Jan 2014 07:46:41 AM All use subject to JSTOR Terms and Conditions PUBLICATIONS OF THE ASTRONOMICAL SOCIETY OF THE PACIFIC, 125:154–182, 2013 February © 2013.
    [Show full text]
  • Four New Exoplanets to Start Off the New Year! 6 January 2012, by Paul Scott Anderson
    Four new exoplanets to start off the new year! 6 January 2012, By Paul Scott Anderson They are all "hot jupiter" type planets, gas giants which orbit very close to their stars and so are much hotter than Earth, like Mercury in our own solar system. Mercury though, of course, is a small rocky world, but in some alien solar systems, gas giants have been found orbiting just as close to their stars, or even closer, than Mercury does here. HAT-P-34b however, may have an "outer component" and is in a very elongated orbit. The other three are more typical hot Jupiters. They were discovered using the transit method, when a planet is aligned in its orbit so that it passes in front of its star, from our viewpoint. Artist's conception of a "hot Jupiter" orbiting close to its star. Credit: NASA/JPL-Caltech/T. Pyle (SSC) So what does this mean? If exoplanet discoveries continue to grow exponentially as expected, then 2012 should be a good year, not only for yet more new planets being found, but also for our It's only a few days into 2012 and already some understanding of these alien worlds and how such new exoplanet discoveries have been announced. a wide variety of solar systems came to be. We've As 2011 ended, there were a total of 716 come a long way from 1992 and the first exoplanet confirmed exoplanets and 2,326 planetary discoveries and things promise to only get more candidates, found by both orbiting space exciting in the future.
    [Show full text]
  • Extra-Solar Planets (Exoplanets)
    ExtraExtra --solarsolar PlanetsPlanets ((ExoplanetsExoplanets )) The search for planets around other stars David Wood Oct 7, 2009 OutlineOutline WhyWhy dodo wewe care?care? OverviewOverview ofof ourour knowledgeknowledge DiscoveryDiscovery techniquestechniques SpaceSpace --basedbased observationsobservations ResultsResults soso farfar ExtraExtra --solarsolar lifelife SummarySummary WhyWhy DoDo WeWe Care?Care? StudiesStudies ofof otherother planetaryplanetary systemssystems greatlygreatly enhanceenhance ourour understandingunderstanding ofof ourour ownown planetaryplanetary systemsystem –– especiallyespecially itsits originorigin andand evolutionevolution WeWe wouldwould likelike toto findfind EarthEarth --likelike planetsplanets andand looklook therethere forfor extraextra --solarsolar lifelife ExoplanetsExoplanets BackgroundBackground TheThe conceptconcept usedused toto bebe theoreticaltheoretical –– therethere OUGHTOUGHT toto bebe otherother planetsplanets FirstFirst discoverydiscovery ofof aa presumedpresumed exoplanetexoplanet inin 19881988 waswas notnot believedbelieved (but(but waswas true)true) SinceSince thethe firstfirst confirmedconfirmed discoverydiscovery inin 1995,1995, thethe raterate ofof discoverydiscovery hashas explodedexploded MoreMore thanthan 370370 exoplanetsexoplanets areare nownow knownknown ExoplanetsExoplanets MostMost ofof thethe knownknown exoplanetsexoplanets areare JupiterJupiter -- likelike (giant(giant gasgas planets)planets) ThisThis isis aa selectionselection effect,effect, sincesince allall
    [Show full text]
  • Exoplanet Detection Techniques
    Fischer D. A., Howard A. W., Laughlin G. P., Macintosh B., Mahadevan S., Sahlmann J., and Yee J. C. (2014) Exoplanet detection techniques. In Protostars and Planets VI (H. Beuther et al., eds.), pp. 715–737. Univ. of Arizona, Tucson, DOI: 10.2458/azu_uapress_9780816531240-ch031. Exoplanet Detection Techniques Debra A. Fischer Yale University Andrew W. Howard University of Hawai‘i at Manoa Greg P. Laughlin University of California at Santa Cruz Bruce Macintosh Stanford University Suvrath Mahadevan The Pennsylvania State University Johannes Sahlmann Université de Genève Jennifer C. Yee Harvard-Smithsonian Center for Astrophysics We are still in the early days of exoplanet discovery. Astronomers are beginning to model the atmospheres and interiors of exoplanets and have developed a deeper understanding of processes of planet formation and evolution. However, we have yet to map out the full com- plexity of multi-planet architectures or to detect Earth analogs around nearby stars. Reaching these ambitious goals will require further improvements in instrumentation and new analysis tools. In this chapter, we provide an overview of five observational techniques that are currently employed in the detection of exoplanets: optical and infrared (IR) Doppler measurements, transit photometry, direct imaging, microlensing, and astrometry. We provide a basic description of how each of these techniques works and discuss forefront developments that will result in new discoveries. We also highlight the observational limitations and synergies of each method and their connections to future space missions. 1. INTRODUCTION novations have advanced the precision for each of these techniques; however, each of the methods have inherent Humans have long wondered whether other solar systems observational incompleteness.
    [Show full text]
  • A Photometric Variability Survey of Field K and M Dwarf Stars With
    Draft version October 25, 2018 A Preprint typeset using LTEX style emulateapj v. 11/10/09 A PHOTOMETRIC VARIABILITY SURVEY OF FIELD K AND M DWARF STARS WITH HATNET J. D. Hartman1, G. A.´ Bakos1, R. W. Noyes1, B. Sipocz˝ 1,2, G. Kovacs´ 3, T. Mazeh4, A. Shporer4, A. Pal´ 1,2 Draft version October 25, 2018 ABSTRACT Using light curves from the HATNet survey for transiting extrasolar planets we investigate the optical broad-band photometric variability of a sample of 27, 560 field K and M dwarfs selected by color and proper-motion (V − K & 3.0, µ > 30 mas/yr, plus additional cuts in J − H vs. H − KS and on the reduced proper motion). We search the light curves for periodic variations, and for large- amplitude, long-duration flare events. A total of 2120 stars exhibit potential variability, including 95 stars with eclipses and 60 stars with flares. Based on a visual inspection of these light curves and an automated blending classification, we select 1568 stars, including 78 eclipsing binaries, as secure variable star detections that are not obvious blends. We estimate that a further ∼ 26% of these stars may be blends with fainter variables, though most of these blends are likely to be among the hotter stars in our sample. We find that only 38 of the 1568 stars, including 5 of the eclipsing binaries, have previously been identified as variables or are blended with previously identified variables. One of the newly identified eclipsing binaries is 1RXS J154727.5+450803, a known P = 3.55 day, late M-dwarf SB2 system, for which we derive preliminary estimates for the component masses and radii of M1 = M2 = 0.258 ± 0.008 M⊙ and R1 = R2 = 0.289 ± 0.007 R⊙.
    [Show full text]
  • Abstract Booklet «Detection and Dynamics of Transiting Exoplanets» 23-27 August 2010, Observatoire De Haute Provence
    Abstract booklet «Detection and dynamics of transiting exoplanets» 23-27 August 2010, Observatoire de Haute Provence Abstracts for talks David Charbonneau (inv) Institute: Harvard Smithsonian Center for Astrophysics, Cambridge Title 2010: The Year We Make (Second) Contact Abstract: The landscale surrounding ground-based surveys for transiting exoplanets has changed dramatically: Eighty transiting exoplanets have been published, dozens more wait in the wings, and both the Corot and Kepler Missions are regularly making new discoveries. The time may soon come when the number of transiting planets discovered from space eclipses that from the ground. I will begin with a review of the recent progress in both ground-based efforts to discover transiting planets, and efforts from both ground and space to characterize these systems. I will then motivate investigations that appear ripe for progress in the coming 5 years, and consider the role of ground-based discovery efforts during this exciting epoch. Coel Hellier and Francesca Faedi Institute: Keele University & Queen's University Belfast Title: New transiting exoplanets and the status of the WASP project. Abstract: We present the current status of the WASP search for transiting exoplanets, focusing on recent planet discoveries from WASP-North, WASP-South and the joint equatorial region, and discuss how these contribute to our understanding of planet parameters and their diversity. We report the results of ongoing monitoring of WASP planets, together with observations of the Rossiter-McLaughlin effect and ground-based and space-based detections of the secondary eclipses. Gaspar Bakos Institute : Harvard-Smithsonian Center for Astrophysics Title : Planets from the HATNet project Abstract : I will summarize the contribution of the HATNet project to transiting extrasolar planet science, highlighting published planets (HAT-P-1b through HAT-P-16b) as well as new discoveries.
    [Show full text]
  • Hatsouth: a Global Network of Fully Automated Identical Wide-Field Telescopes1
    PUBLICATIONS OF THE ASTRONOMICAL SOCIETY OF THE PACIFIC, 125:154–182, 2013 February © 2013. The Astronomical Society of the Pacific. All rights reserved. Printed in U.S.A. HATSouth: A Global Network of Fully Automated Identical Wide-Field Telescopes1 G. Á. BAKOS,2,3,4 Z. CSUBRY,2,3 K. PENEV,2,3 D. BAYLISS,5 A. JORDÁN,6 C. AFONSO,7 J. D. HARTMAN,2,3 T. HENNING,7 G. KOVÁCS,8 R. W. NOYES,3 B. BÉKY,3 V. S UC,6 B. CSÁK,7 M. RABUS,6 J. LÁZÁR,9 I. PAPP,9 P. SÁRI,9 P. C ONROY,5 G. ZHOU,5 P. D. SACKETT,5 B. SCHMIDT,5 L. MANCINI,7 D. D. SASSELOV,3 AND K. UELTZHOEFFER10 Received 2012 June 06; accepted 2012 December 11; published 2013 January 17 ABSTRACT. HATSouth is the world’s first network of automated and homogeneous telescopes that is capable of year-round 24 hr monitoring of positions over an entire hemisphere of the sky. The primary scientific goal of the network is to discover and characterize a large number of transiting extrasolar planets, reaching out to long periods and down to small planetary radii. HATSouth achieves this by monitoring extended areas on the sky, deriving high precision light curves for a large number of stars, searching for the signature of planetary transits, and confirming planetary candidates with larger telescopes. HATSouth employs six telescope units spread over three prime loca- tions with large longitude separation in the southern hemisphere (Las Campanas Observatory, Chile; HESS site, Namibia; Siding Spring Observatory, Australia).
    [Show full text]
  • Planets from the Hatnet Project 3 Al
    Detection and Dynamics of Transiting Exoplanets Proceedings of Haute Provence Observatory Colloquium (23-27 August 2010) Edited by F. Bouchy, R.F. D´ıaz & C. Moutou Planets from the HATNet project G. A.´ Bakos1, J. D. Hartman1, G. Torres1, G. Kov´acs2, R. W. Noyes1, D. W. Latham1, D. D. Sasselov1 & B. B´eky1 1 Harvard-Smithsonian CfA, 60 Garden St., Cambridge, MA, USA [[email protected]] 2 Konkoly Observatory, Budapest Abstract. We summarize the contribution of the HATNet project to extrasolar planet science, highlighting published planets (HAT-P-1b through HAT-P-26b). We also briefly discuss the oper- ations, data analysis, candidate selection and confirmation proce- dures, and we summarize what HATNet provides to the exoplanet community with each discovery. 1. Introduction The Hungarian-made Automated Telescope Network (HATNet; Bakos et al. 2004) survey, has been one of the main contributors to the dis- covery of transiting exoplanets (TEPs), being responsible for approx- imately a quarter of the ∼ 100 confirmed TEPs discovered to date (Fig. 1). It is a wide-field transit survey, similar to other projects such as Super-WASP (Pollaco et al. 2006), XO (McCullough et al. 2005), and TrES (Alonso et al. 2004). The TEPs discovered by these surveys orbit relatively bright stars (V < 13) which allows for precise parameter determination (e.g. mass, radius and eccentricity) and enables follow- up studies to characterize the planets in detail (e.g. studies of planetary arXiv:1101.0322v1 [astro-ph.EP] 1 Jan 2011 atmospheres, or measurements of the sky-projected angle between the orbital axis of the planet and the spin axis of its host star).
    [Show full text]
  • HAT-P-14B: a 2.2 MJ EXOPLANET TRANSITING a BRIGHT F STAR G
    The Astrophysical Journal, 715:458–467, 2010 May 20 doi:10.1088/0004-637X/715/1/458 C 2010. The American Astronomical Society. All rights reserved. Printed in the U.S.A. ∗ HAT-P-14b: A 2.2 MJ EXOPLANET TRANSITING A BRIGHT F STAR G. Torres1,G.A.´ Bakos1,10, J. Hartman1,Geza´ Kovacs´ 2, R. W. Noyes1, D. W. Latham1,D.A.Fischer3,J.A.Johnson4,11, G. W. Marcy5, A. W. Howard5, D. D. Sasselov1, D. Kipping1,6,B.Sipocz˝ 1,7, R. P. Stefanik1, G. A. Esquerdo1, M. E. Everett8,J.Laz´ ar´ 9, I. Papp9,andP.Sari´ 9 1 Harvard-Smithsonian Center for Astrophysics, Cambridge, MA, USA; [email protected] 2 Konkoly Observatory, Budapest, Hungary 3 Department of Physics and Astronomy, San Francisco State University, San Francisco, CA, USA 4 Institute for Astronomy, University of Hawaii, Honolulu, HI, USA 5 Department of Astronomy, University of California, Berkeley, CA, USA 6 Department of Physics and Astronomy, University College London, UK 7 Centre for Astrophysics Research, University of Hertfordshire, Hatfield, UK 8 Planetary Science Institute, Tucson, AZ, USA 9 Hungarian Astronomical Association, Budapest, Hungary Received 2010 February 11; accepted 2010 March 30; published 2010 April 29 ABSTRACT We report the discovery of HAT-P-14b, a fairly massive transiting extrasolar planet orbiting the moderately bright star GSC 3086-00152 (V = 9.98), with a period of P = 4.627669 ± 0.000005 days. The transit is close to +0.007 ± grazing (impact parameter 0.891−0.008) and has a duration of 0.0912 0.0017 days, with a reference epoch of mid-transit of Tc = 2,454,875.28938 ± 0.00047 (BJD).
    [Show full text]