Distillation Theory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Determining Volatile Organic Carbon by Differential Scanning Calorimetry
DETERMINING VOLATILE ORGANIC CARBON BY DIFFERENTIAL SCANNING CALORIMETRY By Roger L. Blaine TA Instrument, Inc. Volatile Organic Carbons (VOCs) are known to have serious environmental effects. Because of these deleterious effects, large scale attempts are being made to measure, reduce and regulate VOC use and emission. The California EPA, for example, requires characterization of the total volatility of pesticides based upon a TGA loss-on-drying test method [1, 2]. In another move, countries of the European market have reached a protocol agreement to reduce and stabilize VOC emissions by the year 2000 to 70% of the 1991 values [3]. And recently the Swiss Federal Government has imposed a tax on the amount of VOC [4]. Such regulatory agreements require qualitative and quantitative tools to assess what is a VOC and how much is present in a given formulation. Chief targets for VOC action include the paints and coatings industries, agricultural pesticides and solvent cleaning processes. VOC’s are defined as those organic materials having a vapor pressure greater than 10 Pa at 20 °C or having corresponding volatility at other operating temperatures associated with industrial processes [3]. Differential scanning calorimetry (DSC) is a useful tool for screening for potential VOC candidates as well as the actual determination of vapor pressure of suspect materials. Both of these measurements are based on the determination of the boiling (or sublimation) temperature; the former under atmospheric conditions, the latter under reduced pressures. Figure 1 725 ° exo 180 C µ size: 10 l 580 prog: 10°C / min atm: N2 Heat Flow Heat Flow 2.25mPa 435 (326 psi) [ ----] Pressure (psi) endo 290 50 100 150 200 250 300 Temperature (°C) TA250 Nielson and co-workers [5] have observed that: • All organic solvents with boiling temperatures below 170 °C are classified as VOCs, and • No organics solvents with boiling temperatures greater than 260 °C are VOCs. -

The Separation of Three Azeotropes by Extractive Distillation by An-I Yeh A
The separation of three azeotropes by extractive distillation by An-I Yeh A thesis submitted in partial fulfillment of the requirement for the degree of Master of Science in Chemical Engineering Montana State University © Copyright by An-I Yeh (1983) Abstract: Several different kinds of extractive distillation agents were investigated to affect the separation of three binary liquid mixtures, isopropyl ether - acetone, methyl acetate - methanol, and isopropyl ether - methyl ethyl ketone. Because of the small size of the extractive distillation column, relative volatilities were assumed constant and the Fenske equation was used to calculate the relative volatilities and the number of minimum theoretical plates. Dimethyl sulfoxide was found to be a good extractive distillation agent. Extractive distillation when employing a proper agent not only negated the azeotropes of the above mixtures, but also improved the efficiency of separation. This process could reverse the relative volatility of isopropyl ether and acetone. This reversion was also found in the system of methyl acetate and methanol when nitrobenzene was the agent. However, normal distillation curves were obtained for the system of isopropyl ether and methyl ethyl ketone undergoing extractive distillation. In the system of methyl acetate and methanol, the relative volatility decreased as the agents' carbon number increased when glycols were used as the agents. In addition, the oxygen number and the locations of hydroxyl groups in the glycols used were believed to affect the values of relative volatility. An appreciable amount of agent must be maintained in the column to affect separation. When dimethyl sulfoxide was an agent for the three systems studied, the relative volatility increased as the addition rate increased. -

Distillation 6
CHAPTER Energy Considerations in Distillation 6 Megan Jobson School of Chemical Engineering and Analytical Science, The University of Manchester, Manchester, UK CHAPTER OUTLINE 6.1 Introduction to energy efficiency ....................................................................... 226 6.1.1 Energy efficiency: technical issues................................................... 227 6.1.1.1 Heating.................................................................................... 227 6.1.1.2 Coolingdabove ambient temperatures...................................... 229 6.1.1.3 Coolingdbelow ambient temperatures ...................................... 230 6.1.1.4 Mechanical or electrical power.................................................. 232 6.1.1.5 Summarydtechnical aspects of energy efficiency ..................... 233 6.1.2 Energy efficiency: process economics............................................... 233 6.1.2.1 Heating.................................................................................... 233 6.1.2.2 Cooling..................................................................................... 235 6.1.2.3 Summarydprocess economics and energy efficiency ............... 237 6.1.3 Energy efficiency: sustainable industrial development........................ 237 6.2 Energy-efficient distillation ............................................................................... 237 6.2.1 Energy-efficient distillation: conceptual design of simple columns...... 238 6.2.1.1 Degrees of freedom in design .................................................. -

A Case Study on Separation of IPA-Water Mixture by Extractive Distillation Using Aspen Plus
International Journal of Advanced Technology and Engineering Exploration, Vol 3(24) ISSN (Print): 2394-5443 ISSN (Online): 2394-7454 Research Article http://dx.doi.org/10.19101/IJATEE.2016.324004 A case study on separation of IPA-water mixture by extractive distillation using aspen plus Sarita Kalla, Sushant Upadhyaya*, Kailash Singh, Rajeev Kumar Dohare and Madhu Agarwal Department of Chemical Engineering, Malaviya National Institute of Technology, Jaipur, India ©2016 ACCENTS Abstract Extractive distillation is one of the popular methods being leveraged to separate isopropyl alcohol (IPA) from water present in waste stream in semi-conductor industries. In this context, the paper aims to carry out simulation study for separation of isopropyl alcohol-water azeotrope mixture using ethylene glycol as entrainer. In particular, temperature, pressure and concentration profile has been studied. Aspen plus® (version 8.8) has been used as simulation tool and optimum number of stages for the simulation turns out to be 42. The results show that top of the column contains IPA of 99.974 mol % purity and bottom product contains water-ethylene glycol mixture. Moreover, sensitivity analysis for different parameters and analysis of residue curve for ternary system have been also performed. Keywords IPA-water, Extractive distillation, Simulation, Entrainer. 1. Introduction 2. Process simulation Isopropyl alcohol is generally used as the cleaning 2.1 Thermodynamic model agent and solvent in chemical industries. Because of Thermodynamic model is used to describe phase its cleaning property it is also known as rubbing equilibria properties of the system. For the design of alcohol. IPA is soluble in water and it forms chemical separation operations the phase equilibrium azeotrope with water at temperature 80.3-80.4 0C. -

Review of Extractive Distillation. Process Design, Operation
Review of Extractive Distillation. Process design, operation optimization and control Vincent Gerbaud, Ivonne Rodríguez-Donis, Laszlo Hegely, Péter Láng, Ferenc Dénes, Xinqiang You To cite this version: Vincent Gerbaud, Ivonne Rodríguez-Donis, Laszlo Hegely, Péter Láng, Ferenc Dénes, et al.. Review of Extractive Distillation. Process design, operation optimization and control. Chemical Engineering Research and Design, Elsevier, 2019, 141, pp.229-271. 10.1016/j.cherd.2018.09.020. hal-02161920 HAL Id: hal-02161920 https://hal.archives-ouvertes.fr/hal-02161920 Submitted on 21 Jun 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Open Archive Toulouse Archive Ouverte OATAO is an open access repository that collects the work of Toulouse researchers and makes it freely available over the web where possible This is an author’s version published in: http://oatao.univ-toulouse.fr/239894 Official URL: https://doi.org/10.1016/j.cherd.2018.09.020 To cite this version: Gerbaud, Vincent and Rodríguez-Donis, Ivonne and Hegely, Laszlo and Láng, Péter and Dénes, Ferenc and You, Xinqiang Review of Extractive Distillation. Process design, operation optimization and control. (2018) Chemical Engineering Research and Design, 141. -

Liquid-Liquid Extraction
OCTOBER 2020 www.processingmagazine.com A BASIC PRIMER ON LIQUID-LIQUID EXTRACTION IMPROVING RELIABILITY IN CHEMICAL PROCESSING WITH PREVENTIVE MAINTENANCE DRIVING PACKAGING SUSTAINABILITY IN THE TIME OF COVID-19 Detecting & Preventing Pressure Gauge AUTOMATIC RECIRCULATION VALVES Failures Schroedahl www.circor.com/schroedahl page 48 LOW-PROFILE, HIGH-CAPACITY SCREENER Kason Corporation www.kason.com page 16 chemical processing A basic primer on liquid-liquid extraction An introduction to LLE and agitated LLE columns | By Don Glatz and Brendan Cross, Koch Modular hemical engineers are often faced with The basics of liquid-liquid extraction the task to design challenging separation While distillation drives the separation of chemicals C processes for product recovery or puri- based upon dif erences in relative volatility, LLE is a fication. This article looks at the basics separation technology that exploits the dif erences in of one powerful and yet overlooked separation tech- the relative solubilities of compounds in two immis- nique: liquid-liquid extraction. h ere are other unit cible liquids. Typically, one liquid is aqueous, and the operations used to separate compounds, such as other liquid is an organic compound. distillation, which is taught extensively in chemical Used in multiple industries including chemical, engineering curriculums. If a separation is feasible by pharmaceutical, petrochemical, biobased chemicals distillation and is economical, there is no reason to and l avor and fragrances, this approach takes careful consider liquid-liquid extraction (LLE). However, dis- process design by experienced chemical engineers and tillation may not be a feasible solution for a number scientists. In many cases, LLE is the best choice as a of reasons, such as: separation technology and well worth searching for a • If it requires a complex process sequence (several quali ed team to assist in its development and design. -

Molecular Corridors and Parameterizations of Volatility in the Chemical Evolution of Organic Aerosols
Atmos. Chem. Phys., 16, 3327–3344, 2016 www.atmos-chem-phys.net/16/3327/2016/ doi:10.5194/acp-16-3327-2016 © Author(s) 2016. CC Attribution 3.0 License. Molecular corridors and parameterizations of volatility in the chemical evolution of organic aerosols Ying Li1,2, Ulrich Pöschl1, and Manabu Shiraiwa1 1Multiphase Chemistry Department, Max Planck Institute for Chemistry, Mainz, Germany 2State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry (LAPC), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China Correspondence to: Manabu Shiraiwa ([email protected]) Received: 23 September 2015 – Published in Atmos. Chem. Phys. Discuss.: 15 October 2015 Revised: 1 March 2016 – Accepted: 3 March 2016 – Published: 14 March 2016 Abstract. The formation and aging of organic aerosols (OA) 1 Introduction proceed through multiple steps of chemical reaction and mass transport in the gas and particle phases, which is chal- lenging for the interpretation of field measurements and lab- Organic aerosols (OA) consist of a myriad of chemical oratory experiments as well as accurate representation of species and account for a substantial mass fraction (20–90 %) OA evolution in atmospheric aerosol models. Based on data of the total submicron particles in the troposphere (Jimenez from over 30 000 compounds, we show that organic com- et al., 2009; Nizkorodov et al., 2011). They influence regional pounds with a wide variety of functional groups fall into and global climate by affecting radiative budget of the at- molecular corridors, characterized by a tight inverse cor- mosphere and serving as nuclei for cloud droplets and ice relation between molar mass and volatility. -

Selection of Thermodynamic Methods
P & I Design Ltd Process Instrumentation Consultancy & Design 2 Reed Street, Gladstone Industrial Estate, Thornaby, TS17 7AF, United Kingdom. Tel. +44 (0) 1642 617444 Fax. +44 (0) 1642 616447 Web Site: www.pidesign.co.uk PROCESS MODELLING SELECTION OF THERMODYNAMIC METHODS by John E. Edwards [email protected] MNL031B 10/08 PAGE 1 OF 38 Process Modelling Selection of Thermodynamic Methods Contents 1.0 Introduction 2.0 Thermodynamic Fundamentals 2.1 Thermodynamic Energies 2.2 Gibbs Phase Rule 2.3 Enthalpy 2.4 Thermodynamics of Real Processes 3.0 System Phases 3.1 Single Phase Gas 3.2 Liquid Phase 3.3 Vapour liquid equilibrium 4.0 Chemical Reactions 4.1 Reaction Chemistry 4.2 Reaction Chemistry Applied 5.0 Summary Appendices I Enthalpy Calculations in CHEMCAD II Thermodynamic Model Synopsis – Vapor Liquid Equilibrium III Thermodynamic Model Selection – Application Tables IV K Model – Henry’s Law Review V Inert Gases and Infinitely Dilute Solutions VI Post Combustion Carbon Capture Thermodynamics VII Thermodynamic Guidance Note VIII Prediction of Physical Properties Figures 1 Ideal Solution Txy Diagram 2 Enthalpy Isobar 3 Thermodynamic Phases 4 van der Waals Equation of State 5 Relative Volatility in VLE Diagram 6 Azeotrope γ Value in VLE Diagram 7 VLE Diagram and Convergence Effects 8 CHEMCAD K and H Values Wizard 9 Thermodynamic Model Decision Tree 10 K Value and Enthalpy Models Selection Basis PAGE 2 OF 38 MNL 031B Issued November 2008, Prepared by J.E.Edwards of P & I Design Ltd, Teesside, UK www.pidesign.co.uk Process Modelling Selection of Thermodynamic Methods References 1. -

Distillation Accessscience from McgrawHill Education
6/19/2017 Distillation AccessScience from McGrawHill Education (http://www.accessscience.com/) Distillation Article by: King, C. Judson University of California, Berkeley, California. Last updated: 2014 DOI: https://doi.org/10.1036/10978542.201100 (https://doi.org/10.1036/10978542.201100) Content Hide Simple distillations Fractional distillation Vaporliquid equilibria Distillation pressure Molecular distillation Extractive and azeotropic distillation Enhancing energy efficiency Computational methods Stage efficiency Links to Primary Literature Additional Readings A method for separating homogeneous mixtures based upon equilibration of liquid and vapor phases. Substances that differ in volatility appear in different proportions in vapor and liquid phases at equilibrium with one another. Thus, vaporizing part of a volatile liquid produces vapor and liquid products that differ in composition. This outcome constitutes a separation among the components in the original liquid. Through appropriate configurations of repeated vaporliquid contactings, the degree of separation among components differing in volatility can be increased manyfold. See also: Phase equilibrium (/content/phaseequilibrium/505500) Distillation is by far the most common method of separation in the petroleum, natural gas, and petrochemical industries. Its many applications in other industries include air fractionation, solvent recovery and recycling, separation of light isotopes such as hydrogen and deuterium, and production of alcoholic beverages, flavors, fatty acids, and food oils. Simple distillations The two most elementary forms of distillation are a continuous equilibrium distillation and a simple batch distillation (Fig. 1). http://www.accessscience.com/content/distillation/201100 1/10 6/19/2017 Distillation AccessScience from McGrawHill Education Fig. 1 Simple distillations. (a) Continuous equilibrium distillation. -

Computer Simulation Applied to Studying Continuous Spirit Distillation and Product Quality Control
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Food Control 22 (2011) 1592e1603 Contents lists available at ScienceDirect Food Control journal homepage: www.elsevier.com/locate/foodcont Computer simulation applied to studying continuous spirit distillation and product quality control Fabio R.M. Batista, Antonio J.A. Meirelles* Laboratory EXTRAE, Department of Food Engineering, Faculty of Food Engineering, University of Campinas e UNICAMP, Campinas, Brazil article info abstract Article history: This work aims to study continuous spirit distillation by computational simulation, presenting some Received 7 June 2010 strategies of process control to regulate the volatile content. The commercial simulator Aspen (Plus and Received in revised form dynamics) was selected. A standard solution containing ethanol, water and 10 minor components rep- 2 March 2011 resented the wine to be distilled. A careful investigation of the vaporeliquid equilibrium was performed Accepted 8 March 2011 for the simulation of two different industrial plants. The simulation procedure was validated against experimental results collected from an industrial plant for bioethanol distillation. The simulations were Keywords: conducted with and without the presence of a degassing system, in order to evaluate the efficiency of Spirits fi Distillation this system in the control of the volatile content. To improve the ef ciency of the degassing system, fl Simulation a control loop based on a feedback controller was developed. The results showed that re ux ratio and Aspen Plus product flow rate have an important influence on the spirit composition. High reflux ratios and spirit Degassing flow rates allow for better control of spirit contamination. -

Distillation Design the Mccabe-Thiele Method Distiller Diagam Introduction
Distillation Design The McCabe-Thiele Method Distiller diagam Introduction • UiUsing r igorous tray-bby-tray callilculations is time consuming, and is often unnecessary. • OikhdfiifbOne quick method of estimation for number of plates and feed stage can be obtained from the graphical McCabe-Thiele Method. • This eliminates the need for tedious calculations, and is also the first step to understanding the Fenske-Underwood- Gilliland method for multi-component distillation • Typi ica lly, the in le t flow to the dis tilla tion co lumn is known, as well as mole percentages to feed plate, because these would be specified by plant conditions. • The desired composition of the bottoms and distillate prodillbifiddhiilldducts will be specified, and the engineer will need to design a distillation column to produce these results. • With the McCabe-Thiele Method, the total number of necessary plates, as well as the feed plate location can biddbe estimated, and some ifiinformation can a lblso be determined about the enthalpic condition of the feed and reflux ratio. • This method assumes that the column is operated under constant pressure, and the constant molal overflow assumption is necessary, which states that the flow rates of liquid and vapor do not change throughout the column. • To understand this method, it is necessary to first elaborate on the subjects of the x-y diagram, and the operating lines used to create the McCabe-Thiele diagram. The x-y diagram • The x-y diagram depi icts vapor-liliqu id equilibrium data, where any point on the curve shows the variations of the amount of liquid that is in equilibrium with vapor at different temperatures. -
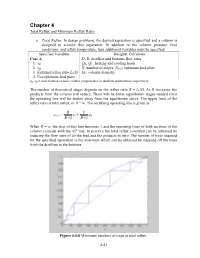
Minimum Reflux Ratio
Chapter 4 Total Reflux and Minimum Reflux Ratio a. Total Reflux . In design problems, the desired separation is specified and a column is designed to achieve this separation. In addition to the column pressure, feed conditions, and reflux temperature, four additional variables must be specified. Specified Variables Designer Calculates Case A D, B: distillate and bottoms flow rates 1. xD QR, QC: heating and cooling loads 2. xB N: number of stages, Nfeed : optimum feed plate 3. External reflux ratio L0/D DC: column diameter 4. Use optimum feed plate xD, xB = mole fraction of more volatile component A in distillate and bottoms, respectively The number of theoretical stages depends on the reflux ratio R = L0/D. As R increases, the products from the column will reduce. There will be fewer equilibrium stages needed since the operating line will be further away from the equilibrium curve. The upper limit of the reflux ratio is total reflux, or R = ∞. The rectifying operating line is given as R 1 yn+1 = xn + xD R +1 R +1 When R = ∞, the slop of this line becomes 1 and the operating lines of both sections of the column coincide with the 45 o line. In practice the total reflux condition can be achieved by reducing the flow rates of all the feed and the products to zero. The number of trays required for the specified separation is the minimum which can be obtained by stepping off the trays from the distillate to the bottoms. Figure 4.4-8 Minimum numbers of trays at total reflux.