1</Sub> Minimization Approach to Sparse Precision Matrix Estimation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cai Guo-Qiang Working on CAI GUO-QIANG BECAME an ARTIST BECAUSE HE DIDN’T WANT an OFFICE JOB
— ARTAND — — VISION — Cai Guo-Qiang working on CAI GUO-QIANG BECAME AN ARTIST BECAUSE HE DIDN’T WANT AN OFFICE JOB. IN 2011 HE EXPLODED 8300 SMOKE SHELLS ‘Falling Back to Earth’ (2013–14) IN DOHA’S GULF DESERT FOR BLACK CEREMONY. HERE CAI GUO-QIANG TALKS ABOUT PLACE, Queensland Art Gallery/Gallery of Modern Art, Brisbane PERFORMANCE AND DODGING PROBLEMS. Photograph Mark Sherwood FALLING BACK TO EARTH: CAI GUO-QIANG NATALIE KING Despite two failed pyrotechnic ‘explosion projects’ for the 1996 and to help dig a new river. After the trench was dug and filled with water, 1999 Asia Pacific Triennials of Contemporary Art (APT), Cai Guo-Qiang everyone went swimming. It was not a foreign idea to me for everyone returned for a more grounded invocation with large-scale installations to take part in a certain activity. If you give people a powerful concept at Queensland Art Gallery/Gallery of Modern Art (QAGOMA), and a goal to strive for, there is a reason to participate. That said, a Brisbane. A gigantic felled eucalyptus tree lies suspended in the gallery, propagandist approach is not the intention of my art because I feel it’s like an environmental relic, while a menagerie of ninety-nine faux life- necessary to have dialogue with the local culture. sized animals are poised to drink at a blue lake. Biblical in scale, this Often I initiate dialogues with local communities. In Australia I Noah’s Ark suggests a harmonious paradise while the number ninety- learnt from Aboriginal elders before creating large-scale gunpowder nine references infinity in Chinese numerology. -

Kūnqǔ in Practice: a Case Study
KŪNQǓ IN PRACTICE: A CASE STUDY A DISSERTATION SUBMITTED TO THE GRADUATE DIVISION OF THE UNIVERSITY OF HAWAI‘I AT MĀNOA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY IN THEATRE OCTOBER 2019 By Ju-Hua Wei Dissertation Committee: Elizabeth A. Wichmann-Walczak, Chairperson Lurana Donnels O’Malley Kirstin A. Pauka Cathryn H. Clayton Shana J. Brown Keywords: kunqu, kunju, opera, performance, text, music, creation, practice, Wei Liangfu © 2019, Ju-Hua Wei ii ACKNOWLEDGEMENTS I wish to express my gratitude to the individuals who helped me in completion of my dissertation and on my journey of exploring the world of theatre and music: Shén Fúqìng 沈福庆 (1933-2013), for being a thoughtful teacher and a father figure. He taught me the spirit of jīngjù and demonstrated the ultimate fine art of jīngjù music and singing. He was an inspiration to all of us who learned from him. And to his spouse, Zhāng Qìnglán 张庆兰, for her motherly love during my jīngjù research in Nánjīng 南京. Sūn Jiàn’ān 孙建安, for being a great mentor to me, bringing me along on all occasions, introducing me to the production team which initiated the project for my dissertation, attending the kūnqǔ performances in which he was involved, meeting his kūnqǔ expert friends, listening to his music lessons, and more; anything which he thought might benefit my understanding of all aspects of kūnqǔ. I am grateful for all his support and his profound knowledge of kūnqǔ music composition. Wichmann-Walczak, Elizabeth, for her years of endeavor producing jīngjù productions in the US. -

Jingjiao Under the Lenses of Chinese Political Theology
religions Article Jingjiao under the Lenses of Chinese Political Theology Chin Ken-pa Department of Philosophy, Fu Jen Catholic University, New Taipei City 24205, Taiwan; [email protected] Received: 28 May 2019; Accepted: 16 September 2019; Published: 26 September 2019 Abstract: Conflict between religion and state politics is a persistent phenomenon in human history. Hence it is not surprising that the propagation of Christianity often faces the challenge of “political theology”. When the Church of the East monk Aluoben reached China in 635 during the reign of Emperor Tang Taizong, he received the favorable invitation of the emperor to translate Christian sacred texts for the collections of Tang Imperial Library. This marks the beginning of Jingjiao (oY) mission in China. In historiographical sense, China has always been a political domineering society where the role of religion is subservient and secondary. A school of scholarship in Jingjiao studies holds that the fall of Jingjiao in China is the obvious result of its over-involvement in local politics. The flaw of such an assumption is the overlooking of the fact that in the Tang context, it is impossible for any religious establishments to avoid getting in touch with the Tang government. In the light of this notion, this article attempts to approach this issue from the perspective of “political theology” and argues that instead of over-involvement, it is rather the clashing of “ideologies” between the Jingjiao establishment and the ever-changing Tang court’s policies towards foreigners and religious bodies that caused the downfall of Jingjiao Christianity in China. This article will posit its argument based on the analysis of the Chinese Jingjiao canonical texts, especially the Xian Stele, and takes this as a point of departure to observe the political dynamics between Jingjiao and Tang court. -

Kathy Siyu Xue, Ph.D., MPH 120 Pine Bark Ln Athens, GA 30605 (706) 353-7609 [email protected]
Kathy Siyu Xue, Ph.D., MPH 120 Pine Bark Ln Athens, GA 30605 (706) 353-7609 [email protected] EDUCATION Doctorate of Philosophy 2012-2017 Interdisciplinary Toxicology Program Athens, GA Department of Environmental Health Sciences University of Georgia Master of Public Health 2014-2017 University of Georgia Athens, GA Bachelor of Science 2008-2012 Cell and Molecular Biology Austin, TX University of Texas – Austin WORK EXPERIENCE 2017- present Postdoctoral Researcher, University of Georgia, Athens, GA. Mentor: Dr. Jia-Sheng Wang Jun. 2016 – Aug. 2016 Internship, United State Department of Agriculture Toxicology and Mycotoxin Research Unit, Athens, GA Site Supervisor: Dr. Kenneth Voss 2012-2017 Research Assistant, University of Georgia, Athens, GA. Advisor: Dr. Jia-Sheng Wang Aug.2013- Dec. 2013 Teaching Assistant, University of Georgia, Athens, GA. Taking roll, organizing student seminars, coordinating speakers Mar. 2012 – May 2012 Undergraduate Research Volunteer, Dr. Mueller Lab University of Texas – Austin, TX 2010 – 2012 Student Volunteer, Athens Regional Medical Center, Athens, GA 2010-2011 Student Research Assistant, University of Georgia – Athens, GA Dr. Jia-sheng Wang Lab Refill pipette tips, organize chemicals, shadowing research scientists. Additional work including culturing and toxicity testing for C elegans, assistance in oxidative damage biomarker analysis. 2004-2007 Student Volunteer, Texas Tech University – Lubbock, TX Dr. Jia-Sheng Wang Lab HONOR AND AWARDS 2017 Induction into Beta Chi Chapter of Delta Omega Honorary Society -

Ideophones in Middle Chinese
KU LEUVEN FACULTY OF ARTS BLIJDE INKOMSTSTRAAT 21 BOX 3301 3000 LEUVEN, BELGIË ! Ideophones in Middle Chinese: A Typological Study of a Tang Dynasty Poetic Corpus Thomas'Van'Hoey' ' Presented(in(fulfilment(of(the(requirements(for(the(degree(of(( Master(of(Arts(in(Linguistics( ( Supervisor:(prof.(dr.(Jean=Christophe(Verstraete((promotor)( ( ( Academic(year(2014=2015 149(431(characters Abstract (English) Ideophones in Middle Chinese: A Typological Study of a Tang Dynasty Poetic Corpus Thomas Van Hoey This M.A. thesis investigates ideophones in Tang dynasty (618-907 AD) Middle Chinese (Sinitic, Sino- Tibetan) from a typological perspective. Ideophones are defined as a set of words that are phonologically and morphologically marked and depict some form of sensory image (Dingemanse 2011b). Middle Chinese has a large body of ideophones, whose domains range from the depiction of sound, movement, visual and other external senses to the depiction of internal senses (cf. Dingemanse 2012a). There is some work on modern variants of Sinitic languages (cf. Mok 2001; Bodomo 2006; de Sousa 2008; de Sousa 2011; Meng 2012; Wu 2014), but so far, there is no encompassing study of ideophones of a stage in the historical development of Sinitic languages. The purpose of this study is to develop a descriptive model for ideophones in Middle Chinese, which is compatible with what we know about them cross-linguistically. The main research question of this study is “what are the phonological, morphological, semantic and syntactic features of ideophones in Middle Chinese?” This question is studied in terms of three parameters, viz. the parameters of form, of meaning and of use. -

English Versions of Chinese Authors' Names in Biomedical Journals
Dialogue English Versions of Chinese Authors’ Names in Biomedical Journals: Observations and Recommendations The English language is widely used inter- In English transliteration, two-syllable Forms of Chinese Authors’ Names nationally for academic purposes. Most of given names sometimes are spelled as two in Biomedical Journals the world’s leading life-science journals are words (Jian Hua), sometimes as one word We recently reviewed forms of Chinese published in English. A growing number (Jianhua), and sometimes hyphenated authors’ names accompanying English- of Chinese biomedical journals publish (Jian-Hua). language articles or abstracts in various abstracts or full papers in this language. Occasionally Chinese surnames are Chinese and Western biomedical journals. We have studied how Chinese authors’ two syllables (for example, Ou-Yang, Mu- We found considerable inconsistency even names are presented in English in bio- Rong, Si-Ma, and Si-Tu). Editors who are within the same journal or issue. The forms medical journals. There is considerable relatively unfamiliar with Chinese names were in the following categories: inconsistency. This inconsistency causes may mistake these compound surnames for • Surname in all capital letters followed by confusion, for example, in distinguishing given names. hyphenated or closed-up given name, for surnames from given names and thus cit- China has 56 ethnic groups. Names example, ing names properly in reference lists. of minority group members can differ KE Zhi-Yong (Chinese Journal of In the current article we begin by pre- considerably from those of Hans, who Contemporary Pediatrics) senting as background some features of constitute most of the Chinese population. GUO Liang-Qian (Chinese Chinese names. -

Huaqiang ZENG Team Leader and Principal Research Scientist
Huaqiang ZENG Team Leader and Principal Research Scientist +65 6824 7115 [email protected] Team Leader and Principal Research Scientist, NanoBio Lab, Singapore, 2019-present Team Leader and Principal Research Scientist, Institute of Bioengineering and Nanotechnology, Singapore, 2014-2019 Assistant Professor, National University of Singapore, 2006-2013 Postdoctoral Research Fellow, The Scripps Research Institute, USA, 2002-2006 Ph.D. in Organic Chemistry, The State University of New York at Buffalo, USA, 2002 B.S. in Chemical Physics, The University of Science and Technology of China, 1996 Publications 1. A. Roy, H. Joshi, R. Ye, J. Shen, F. Chen, A. Aksimentiev and H. Zeng, “Polyhydrazide‐Based Organic Nanotubes as Efficient and Selective Artificial Iodide Channels,” Angewandte Chemie International Edition, 132 (2020) 4836-4843. IF 12.102 2. J. Shen, J. Fan, R. Ye, N. Li, Y. Mu and H. Zeng, “Polypyridine-Based Helical Amide Foldamer Channels for Rapid Transport of Water and Proton with High Ion Rejection,” Angewandte Chemie International Edition, (2020) DOI: 10.1002/anie.202003512. IF 12.257 3. J. Shen, R. Ye, A. Romanies, A. Roy, F. Chen, C. Ren, Z. Liu and H. Zeng, “An Aquafoldmer-Based Aquaporin-Like Synthetic Water Channel,” Journal of the American Chemical Society, 142 (2020) 10050-10058. IF 14.695 4. H. Zeng, A. Roy, H. Joshi, R. Ye, J. Shen, F. Chen and A. Aksimentiev, “Polyhydrazide-Based Organic Nanotubes as Extremely Efficient and Highly Selective Artificial Iodide Channels,” Angew. Chem. Int. Ed., (2020) DOI: 10.1002/anie.201916287 5. H. Zeng, F. Chen, J. Shen, N. Li, A. -

Using Online Applications to Improve Tone Perception Among L2 Learners of Chinese (网络应用对中文二语学习者声调辨识的有效性研究)
Journal of Technology and Chinese Language Teaching Volume 10 Number 1, June 2019 http://www.tclt.us/journal/2019v10n1/xulili.pdf pp. 26-56 Using Online Applications to Improve Tone Perception among L2 Learners of Chinese (网络应用对中文二语学习者声调辨识的有效性研究) Xu, Hongying Li, Yan Li, Yingjie (徐红英) (李艳) (李颖颉) University of University of University of Colorado- Wisconsin-La Crosse Kansas Boulder (威斯康星大学拉克 (堪萨斯大学) (科罗拉多大学博尔得分 罗校区) [email protected] 校) [email protected] [email protected] Abstract: This study investigated the effectiveness of an online application in helping beginning-level Chinese learners improve their perception of the tones in Mandarin Chinese. Two groups—one experimental and one traditional—of beginning Chinese learners from two universities in the Midwest participated in this study. The experimental group (n=20) used the online application to practice tones for four 15-minute sessions in class. The traditional group (n=11) participated in traditional instructor-led practice in class in lieu of the online practice. Both groups completed a pre-test, an immediately administered post-test, and a delayed post-test designed to assess their perception of the tones of monosyllabic and disyllabic words. No statistically significant difference has been found between the two groups in their tone perception performance in the post-test and in the delayed post-test. However, the experimental group showed a positive trend in improving their perception on those tones which posed more difficulty than others. Their experience with this online application and the pronunciation learning strategies of participants in the experimental group were also examined through a survey. Based on the findings, it is proposed that the use of online tone practice is worthwhile in a Chinese language class, but might fit better into the curriculum as external assignments. -
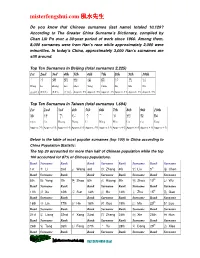
Misterfengshui.Com 風水先生
misterfengshui.com 風水先生 Do you know that Chinese surnames (last name) totaled 10,129? According to The Greater China Surname’s Dictionary, compiled by Chan Lik Pu over a 30-year period of work since 1960. Among them, 8,000 surnames were from Han’s race while approximately 2,000 were minorities. In today’s China, approximately 3,000 Han’s surnames are still around. Top Ten Surnames In Beijing (total surnames 2,225) 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 王 李 張 劉 趙 楊 陳 徐 馬 吳 Wang Li Zhang Liu Zhao Yang Chen Xu Ma Wu (10.6% ) (9.6%) (9.6%) (7.7% ) Approx. 5% Approx. 5% Approx. 4% Approx. 4% Approx. 4% Approx. 3% Top Ten Surnames In Taiwan (total surnames 1,694) 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 陳 林 黃 張 李 王 吳 劉 蔡 楊 Chen Lin Huang Zhang Li Wang Wux. Liu Cai Yang Approx .7% Approx 6 % Approx 6 % Approx 6 % Approx. 5% Approx 5 % Approx 4 % Approx 4 % Approx 4 % Approx 4 % Below is the table of most popular surnames (top 100) in China according to China Population Statistic: The top 20 accounted for more than half of Chinese population while the top 100 accounted for 87% of Chinese populations. Rank Surname Rank Rank Surname Rank Surname Rank Surname 1st 李 Li 2nd 王 Wang 3rd 張 Zhang 4th 劉 Liu 5th 陳 Chen Rank Surname Rank Rank Surname Rank Surname Rank Surname 6th 楊 Yang 7th 趙 Zhao 8th 黃 Huang 9th 周 Zhou 10 th 吳 Wu Rank Surname Rank Rank Surname Rank Surname Rank Surname 11th 徐 Xu 12th 孫 Sun 13th 胡 Hu 14th 朱 Zhu 15 th 高 Gao Rank Surname Rank Rank Surname Rank Surname Rank Surname 16th 林 Lin 17th 何 He 18th 郭 Guo 19th 馬 Ma 20 th 羅 Luo Rank -

Sir David Adjaye and Cai Guo-Qiang to Receive 2020 Isamu Noguchi Award
FOR IMMEDIATE RELEASE [email protected] 718.204.7088 x 206 Sir David Adjaye and Cai Guo-Qiang to Receive 2020 Isamu Noguchi Award Award to be presented in a virtual celebration as part of The Noguchi Museum’s annual benefit on November 16, 2020 Sir David Adjaye OBE. Photo: Chris Schwagga Cai Guo-Qiang. Photo: Lin Yi, courtesy Cai Studio WHAT New York, NY (September 14, 2020) — The Noguchi Museum will present the 2020 Isamu Noguchi Award to architect Sir David Adjaye OBE and artist Cai Guo-Qiang in a virtual celebration on Monday, November 16, 2020, at 8 pm EST. Previously planned for May 19, 2020, the Museum’s annual benefit and Isamu Noguchi Award presentation was postponed due to the pandemic. In its seventh year, the Isamu Noguchi Award is conferred on individuals who share Noguchi’s spirit of innovation, global consciousness, and commitment to Eastern and Western cultural exchange. noguchi.org/award WHO Widely recognized as one of the leading architects of his generation, Ghanaian-British architect Sir David Adjaye OBE has received international acclaim for his impact on the field. Adjaye, who was born in Tanzania to Ghanaian parents in 1966, cites influences ranging from contemporary art, music, and science, to African art forms and the civic life of cities. In 2000, he founded Adjaye Associates, which today has projects spanning the globe. In 2017, he was knighted by Queen Elizabeth II. 1 of 3 Adjaye is widely viewed as an architect with an artist’s sensibility and vision. Also like Noguchi, he is committed to a multidisciplinary practice, with projects ranging from private houses, bespoke furniture collections, product design, exhibitions, and temporary pavilions to major arts centers, civic buildings, and master plans. -

Names of Chinese People in Singapore
101 Lodz Papers in Pragmatics 7.1 (2011): 101-133 DOI: 10.2478/v10016-011-0005-6 Lee Cher Leng Department of Chinese Studies, National University of Singapore ETHNOGRAPHY OF SINGAPORE CHINESE NAMES: RACE, RELIGION, AND REPRESENTATION Abstract Singapore Chinese is part of the Chinese Diaspora.This research shows how Singapore Chinese names reflect the Chinese naming tradition of surnames and generation names, as well as Straits Chinese influence. The names also reflect the beliefs and religion of Singapore Chinese. More significantly, a change of identity and representation is reflected in the names of earlier settlers and Singapore Chinese today. This paper aims to show the general naming traditions of Chinese in Singapore as well as a change in ideology and trends due to globalization. Keywords Singapore, Chinese, names, identity, beliefs, globalization. 1. Introduction When parents choose a name for a child, the name necessarily reflects their thoughts and aspirations with regards to the child. These thoughts and aspirations are shaped by the historical, social, cultural or spiritual setting of the time and place they are living in whether or not they are aware of them. Thus, the study of names is an important window through which one could view how these parents prefer their children to be perceived by society at large, according to the identities, roles, values, hierarchies or expectations constructed within a social space. Goodenough explains this culturally driven context of names and naming practices: Department of Chinese Studies, National University of Singapore The Shaw Foundation Building, Block AS7, Level 5 5 Arts Link, Singapore 117570 e-mail: [email protected] 102 Lee Cher Leng Ethnography of Singapore Chinese Names: Race, Religion, and Representation Different naming and address customs necessarily select different things about the self for communication and consequent emphasis. -

Prof. Wei-Cai Zeng PH. D
Prof. Wei-Cai Zeng PH. D. Antioxidant Polyphenols Team, Department of Food Engineering, Sichuan University Chengdu 610065, P. R. China EDUCATION Sichuan University, Chengdu, P. R. China Doctor Degree 2011 Major: Food Science Sichuan University, Chengdu, P. R. China Master Degree 2008 Major: Food Science Sichuan University, Chengdu, P. R. China Bachelor Degree 2005 Major: Food Science and Technology AWARDS • Academic Award for Distinguished Doctor, Ministry of Education, China 2014 • Outstanding Researcher Award, Sichuan University 2012 RESEARCH EXPERIENCE Department of Food Engineering, Sichuan University, Chengdu, P. R. China Professor, Head of the Teaching and Research Section 2014- LANGUAGES • English • Chinese MEMBERSHIPS • Chinese Institute of Food Science and Technology • China Animal Product Processing Research Institute • Sichuan Nutrition Society RESEARCH WORK More than 80 academic research papers have been published, including 33 SCI (total IF>80) and 2 authorized national invention patents. The main research areas are food chemistry. Some English Publications: [1] Hao-Xiang Gao, Zheng He, Qun Sun, Qiang He, Wei-Cai Zeng*. A functional polysaccharide film forming by pectin, chitosan, and tea polyphenols [J]. Carbohydrate Polymers, 2019, 215: 1-7. [2] Mai-Rui Gao, Qian-Da Xu, Qiang He, Qun Sun, Wei-Cai Zeng*. A theoretical and experimental study: the influence of different standards on the determination of total phenol content in the Folin-Ciocalteu assay [J]. Journal of Food Measurement and Characterization, 2019, 13(2): 1349-1356. [3] ShaoBo Li, Wei-Cai Zeng, Ruolin Li, Louwrens C. Hoffman, Zhifei He, Qun Sunb, Hongjun Li. Rabbit meat production and processing in China [J]. Meat Science, 2018, 145: 320-328.