DOCSLIB.ORG

Systematic Design of Antennas Using the Theory of Characteristic Modes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Systematic Design of Antennas Using the Theory of Characteristic Modes Ph. D. Dissertation SYSTEMATIC DESIGN OF ANTENNAS USING THE THEORY OF CHARACTERISTIC MODES Author: Marta Cabedo Fabrés Advisor: Alejandro Valero Nogueira February 2007 To my parents. To José Manuel. iii Acknowledgements I would like to express my sincere gratitude and appreciation to my advisor Alejandro Valero for his expert guidance, patience, and keen interest throughout the course of this work. He has taught me to do my research in an organized and meticulous way. I am also grateful to Miguel Ferrando not only for his help and valuable suggestions for this thesis, but also for his advice and support in my professional career. I am especially indebted to my faithful colleague Eva Antonino, for her friendship, support and encouragement. Without her help this work would have been a lot harder. I would like to thank José Ignacio Herranz for sharing with me his optimism and intelligence. He is always willing to help anyone. Acknowledgements are also due to Mariano Baquero and Vicent Miquel Rodrigo, and to the fellow companions at GRE laboratory, Bernat, Esperanza, Daniel, David, Carlos, Fulvio, and Felipe, for their support and friendship. My parents and my family stood behind me for which I am thankful for them forever. Finally, to my beloved husband José Manuel go my most loving thanks for his patience, understanding and unlimited encouragement. Marta Cabedo Fabrés Ph. D. Dissertation iv Marta Cabedo Fabrés Ph. D. Dissertation v Abstract The main goal of this thesis is to show how the Theory of Characteristic Modes can be systematically applied to design wire and planar antennas. Through numerous examples, it will be demonstrated that in contrast with other classical design methods, the Theory of Characteristic Modes brings insight into the physical phenomena taking place on an antenna. Examples will be presented in order to demonstrate that an in depth knowledge of the radiating mechanisms of very basic antennas helps to design novel antennas on a clear and rational basis. It will be also explained how the information given by characteristic modes can be used for the selection of the most suitable shape for the radiating element, as well as for the choice of an optimum feeding arrangement to maximize the impedance bandwidth. The Theory of Characteristic Modes was first formulated by Garbacz in 1968, and later refined by Harrington and Mautz in 1971. Traditionally, characteristic modes have been applied to antenna shape synthesis, and control of obstacle scattering by reactive loading. However, at present, the Theory of Characteristic Modes has practically fallen into disuse, in spite of the fact that it leads to modal solutions, which are particularly useful in problems involving analysis, synthesis and optimization of antennas and scatterers. Characteristic modes are real current modes that correspond with the eigenvectors of a particular weighted eigenvalue equation that involves the generalized impedance matrix of the body. Thus, characteristic modes can be computed numerically for conducting bodies of arbitrary shape, and since they form a set of orthogonal functions, they can be used to expand the total current on the surface of the body. However, what makes characteristic modes really attractive for antenna design is the physical insight they bring into the radiating phenomena taking place in the antenna. Associated to each characteristic mode there is an eigenvalue whose magnitude provides information about the resonant frequency and radiating characteristics of modes. Additionally, since characteristic modes are computed in the absence of any kind of excitation, they only depend on the shape and size of the conducting object. Hence, antenna design using characteristic modes can be performed in a controlled way following two steps: - Firstly, the shape and size of the radiating element are optimized on the base of the information provided by eigenvalues. - Next, studying the current distribution of modes an optimum feeding arrangement is chosen so that the desired mode or modes may be excited, in order to obtain a specific radiating behaviour. Marta Cabedo Fabrés Ph. D. Dissertation vi Marta Cabedo Fabrés Ph. D. Dissertation vii Resumen El principal objetivo de esta tesis es demostrar que la Teoría de los Modos Característicos puede ser empleada de forma sistemática para diseñar antenas de hilo y antena planas. La gran ventaja de los modos característicos, frente a otros métodos de diseño, es la clara visión física que proporcionan de los fenómenos que contribuyen a la radiación de la antena. A través de numerosos ejemplos se demostrará como los modos característicos permiten comprender mejor el funcionamiento de una antena, de forma que el diseño de la misma se puede realizar de forma justificada y coherente. También se mostrará como la información proporcionada por los modos característicos puede ser aprovechada para seleccionar la forma más apropiada para el elemento radiante, al igual que para elegir una configuración de alimentación óptima que maximice el ancho de banda de impedancia. La Teoría de los Modos Característicos fue inicialmente formulada por Garbacz en 1968, y posteriormente refinada por Harrington y Mautz en 1971. Tradicionalmente, los modos característicos han sido empleados para sintetizar formas de antena, y para controlar la difracción de objetos mediante carga reactiva. Sin embargo, en la actualidad, la Teoría de los Modos Característicos ha caído prácticamente en el olvido, a pesar de que permite obtener una solución modal para la corriente, que es de gran utilidad a la hora de analizar problemas de análisis, síntesis y optimización de antenas y difractores. La Teoría de los Modos Característicos parte de la definición de un problema de autovalores que involucra la matriz de impedancia generalizada de la estructura, y que tras ser resuelto proporciona un conjunto de modos de corriente reales, que son los denominados modos característicos. Estos modos se corresponden con las resonancias naturales de la estructura y pueden ser obtenidos numéricamente para cuerpos conductores de forma arbitraria. Por otra parte, los modos característicos forman un conjunto de funciones cerrado y ortogonal, por lo que pueden ser empleados para expandir la corriente superficial que fluye por el cuerpo conductor. Sin embargo, lo que hace a los modos característicos especialmente atractivos para el diseño de antenas es la visión física que aportan de los fenómenos de radiación que determinan el comportamiento de la antena. Asociado a cada modo característicos existe un autovalor, cuya magnitud proporciona información sobre la frecuencia de resonancia y las propiedades de radiación de los modos. Además, puesto que los modos característicos se calculan en ausencia de cualquier excitación, únicamente dependen de la forma y del tamaño del cuerpo conductor. Por tanto, el diseño de la antena se puede llevar a cabo de forma controlada en dos pasos: Marta Cabedo Fabrés Ph. D. Dissertation viii - En primer lugar, se optimiza la forma y el tamaño del elemento radiante en base a la información proporcionada por los autovalores. - A continuación, a partir del estudio de la distribución de corriente de los modos se determina una configuración de alimentación óptima que permita excitar el modo o modos deseados, con el fin de obtener un comportamiento radiante determinado. Marta Cabedo Fabrés Ph. D. Dissertation ix Resum El principal objectiu d’aquesta tesi és demostrar que la Teoria dels Modes Característics pot ser emprada de forma sistemàtica per a disenyar antenes de fil i antenes planes. El gran avantatge dels modes característics, enfront d'altres mètodes de disseny, és la clara visió física que proporcionen dels fenòmens que contribuïxen a la radiació de l'antena. Mitjançant nombrosos exemples es demostrarà com els modes característics permeten comprendre millor el funcionament d'una antena, de manera que el disseny de la mateixa es pot realitzar de forma justificada i coherent. També es mostrarà com la informació proporcionada pels modes característics pot ser aprofitada per a seleccionar la forma més apropiada per a l'element radiant, igual que per a triar una configuració d'alimentació òptima que maximitze l'ample de banda d'impedància. La Teoria dels Modes Característics va ser inicialment formulada per Garbacz en 1968, i posteriorment refinada per Harrington i Mautz en 1971. Tradicionalment, els modes característics han sigut emprats per a sintetitzar formes d'antena, i per a controlar la difracció d'objectes per mitjà de càrrega reactiva. No obstant, en l'actualitat, la Teoria dels Modes Característics ha caigut pràcticament en l'oblit, a pesar que permet obtindre una solució modal per al corrent, que és de gran utilitat a l'hora d'analitzar problemes d'anàlisi, síntesi i optimització d'antenes i difractors. La Teoria dels Modes Característics partix de la definició d'un problema d'autovalors que involucra la matriu d'impedància generalitzada de l'estructura, i que després de ser resolt proporciona un conjunt de modes de corrent real, que són els denominats modes característics. Estos modes es corresponen amb les ressonàncies naturals de l'estructura i poden ser obtinguts numèricament per a cossos conductors de forma arbitrària. D'altra banda, els modes característics formen un conjunt de funcions tancat i ortogonal, per la qual cosa poden ser emprats per a expandir el corrent superficial que fluïx pel cos conductor. No obstant, allò que fa als modes característics especialment atractius per al disseny d'antenes és la visió física que aporten dels fenòmens de radiació que determinen el comportament de l'antena. Associat a cada mode característics hi ha un autovalor, la magnitud del qual proporciona informació sobre la freqüència de ressonància i les propietats de radiació dels modes. A més, ja que els modes característics es calculen en absència de qualsevol excitació, únicament depenen de la forma i de la grandària del cos conductor. Per tant, el disseny de l'antena es pot dur a terme de forma controlada en dos passos: Marta Cabedo Fabrés Ph.
Load more

Recommended publications
  • The Role of Anti-Resonance Frequencies from Operational Modal Analysis in finite Element Model Updating
    ARTICLE IN PRESS Mechanical Systems and Signal Processing Mechanical Systems and Signal Processing 21 (2007) 74–97 www.elsevier.com/locate/jnlabr/ymssp The role of anti-resonance frequencies from operational modal analysis in finite element model updating D. Hansona,Ã, T.P. Watersb, D.J. Thompsonb, R.B. Randalla, R.A.J. Forda aUniversity of New South Wales, Sydney, Australia bInstitute of Sound and Vibration Research, Universtiy of Southampton, UK Received 13 September 2005; received in revised form 29 December 2005; accepted 4 January 2006 Available online 15 March 2006 Abstract Finite element model updating traditionally makes use of both resonance and modeshape information. The mode shape information can also be obtained from anti-resonance frequencies, as has been suggested by a number of researchers in recent years. Anti-resonance frequencies have the advantage over mode shapes that they can be much more accurately identified from measured frequency response functions. Moreover, anti-resonance frequencies can, in principle, be estimated from output-only measurements on operating machinery. The motivation behind this paper is to explore whether the availability of anti-resonances from such output-only techniques would add genuinely new information to the model updating process, which is not already available from using only resonance frequencies. This investigation employs two-degree-of-freedom models of a rigid beam supported on two springs. It includes an assessment of the contribution made to the overall anti-resonance sensitivity by the mode shape components, and also considers model updating through Monte Carlo simulations, experimental verification of the simulation results, and application to a practical mechanical system, in this case a petrol generator set.
    [Show full text]
  • MECHANICS Don, Don, 2020- N
    Vestnik of Don State Technical University. 2020. Vol. 20, no. 2, pp. 118–124. ISSN 1992-5980 eISSN 1992-6006 MECHANICS UDC 539.3 https://doi.org/10.23947/1992-5980-2020-20-2-118-124 Transverse vibrations of a circular bimorph with piezoelectric and piezomagnetic layers A. N. Solov'ev, Do Thanh Binh, O. N. Lesnyak Don State Technical University (Rostov-on-Don, Russian Federation) Introduction. Transverse axisymmetric oscillations of a bimorph with two piezo-active layers, piezoelectric and piezomagnetic, are studied. This element can be applied in an energy storage device which is in an alternating magnetic field. The work objective is to study the dependence of resonance and antiresonance frequencies, and electromechanical coupling factor, on the geometric parameters of the element. Materials and Methods. A mathematical model of the piezoelement action is a boundary value problem of linear magneto-electro-elasticity. The element consists of three layers: two piezo-active layers (PZT-4 and CoFe2O4) and a centre dead layer made of steel. The finite element method implemented in the ANSYS package is used as a method for solving a boundary value problem. Results. A finite element model of a piezoelement in the ANSYS package is developed. Problems of determining the natural frequencies of resonance and antiresonance are solved. Graphic dependences of these frequencies and the electromechanical coupling factor on the device geometrics, the thickness and radius of the piezo-active layers, are constructed. Discussion and Conclusions. The results obtained can be used under designing the working element of the energy storage device due to the action of an alternating magnetic field.
    [Show full text]
  • A Review of Electric Impedance Matching Techniques for Piezoelectric Sensors, Actuators and Transducers
    Review A Review of Electric Impedance Matching Techniques for Piezoelectric Sensors, Actuators and Transducers Vivek T. Rathod Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI 48824, USA; [email protected]; Tel.: +1-517-249-5207 Received: 29 December 2018; Accepted: 29 January 2019; Published: 1 February 2019 Abstract: Any electric transmission lines involving the transfer of power or electric signal requires the matching of electric parameters with the driver, source, cable, or the receiver electronics. Proceeding with the design of electric impedance matching circuit for piezoelectric sensors, actuators, and transducers require careful consideration of the frequencies of operation, transmitter or receiver impedance, power supply or driver impedance and the impedance of the receiver electronics. This paper reviews the techniques available for matching the electric impedance of piezoelectric sensors, actuators, and transducers with their accessories like amplifiers, cables, power supply, receiver electronics and power storage. The techniques related to the design of power supply, preamplifier, cable, matching circuits for electric impedance matching with sensors, actuators, and transducers have been presented. The paper begins with the common tools, models, and material properties used for the design of electric impedance matching. Common analytical and numerical methods used to develop electric impedance matching networks have been reviewed. The role and importance of electrical impedance matching on the overall performance of the transducer system have been emphasized throughout. The paper reviews the common methods and new methods reported for electrical impedance matching for specific applications. The paper concludes with special applications and future perspectives considering the recent advancements in materials and electronics.
    [Show full text]
  • Maintenance of Remote Communication Facility (Rcf)
    ORDER rlll,, J MAINTENANCE OF REMOTE commucf~TIoN FACILITY (RCF) EQUIPMENTS OCTOBER 16, 1989 U.S. DEPARTMENT OF TRANSPORTATION FEDERAL AVIATION AbMINISTRATION Distribution: Selected Airway Facilities Field Initiated By: ASM- 156 and Regional Offices, ZAF-600 10/16/89 6580.5 FOREWORD 1. PURPOSE. direction authorized by the Systems Maintenance Service. This handbook provides guidance and prescribes techni- Referenceslocated in the chapters of this handbook entitled cal standardsand tolerances,and proceduresapplicable to the Standardsand Tolerances,Periodic Maintenance, and Main- maintenance and inspection of remote communication tenance Procedures shall indicate to the user whether this facility (RCF) equipment. It also provides information on handbook and/or the equipment instruction books shall be special methodsand techniquesthat will enablemaintenance consulted for a particular standard,key inspection element or personnel to achieve optimum performancefrom the equip- performance parameter, performance check, maintenance ment. This information augmentsinformation available in in- task, or maintenanceprocedure. struction books and other handbooks, and complements b. Order 6032.1A, Modifications to Ground Facilities, Order 6000.15A, General Maintenance Handbook for Air- Systems,and Equipment in the National Airspace System, way Facilities. contains comprehensivepolicy and direction concerning the development, authorization, implementation, and recording 2. DISTRIBUTION. of modifications to facilities, systems,andequipment in com- This directive is distributed to selectedoffices and services missioned status. It supersedesall instructions published in within Washington headquarters,the FAA Technical Center, earlier editions of maintenance technical handbooksand re- the Mike Monroney Aeronautical Center, regional Airway lated directives . Facilities divisions, and Airway Facilities field offices having the following facilities/equipment: AFSS, ARTCC, ATCT, 6. FORMS LISTING. EARTS, FSS, MAPS, RAPCO, TRACO, IFST, RCAG, RCO, RTR, and SSO.
    [Show full text]
  • THE UNIVERSITY, BRISTOL, BS8 Lhr, ENGLAND DEVELOPMENT of ANTIRESONANCE FORCE ISOLATORS for HELICOPTER VIBRATION REDUCTION
    SIXTH EUROPEAN ROTORCRAFT AND POWERED LIFT AIRCRAFT FORUM PAPER NO, 18 DEVELOPMENT OF ANTIRESONANCE FORCE ISOLATORS FOR HELICOPTER VIBRATION REDUCTION D. Braun Messerschmitt-Bolkow-Blohm GmbH Munich, Germany September 16-19, 1980 Bristol, England THE UNIVERSITY, BRISTOL, BS8 lHR, ENGLAND DEVELOPMENT OF ANTIRESONANCE FORCE ISOLATORS FOR HELICOPTER VIBRATION REDUCTION D. Braun Messerschmitt-B6lkow-Blohm GmbH Munich, Germany Abstract One method of reduction of the rotor induced cabin vibrations consists of seperating the helicopter fuselage dynamically from the rotor-transmission unit by use of convenient isolator elements. An example of such a device is one which is essentially formed by the parallel connection of a spring and a passive force generator, and which works according to the well known antiresonance principle. This paper deals with the development of two different types of uni­ axial antiresonance force isolators. They are suitably arranged at several points, in different operating directions, as connecting members between gearbox and fuselage, to obtain multiaxis vibration isolation. One of these isolators is a conventional model; the other one is a novel type distingui­ shed by very low inherent damping, total symmetrical arrangement of all com­ ponents, and simple wear-resistant design. Sufficiently exact theoretical descriptions are developed for both isolator types. The effectiveness of the presented force isolators is tested by use of an uniaxial functional model by which the free-free condition of the flying helicopter
    [Show full text]
  • On Antiresonance in the Forced Response of Mistuned Bladed Disks
    Shock and Vibration 10 (2003) 135–146 135 IOS Press On antiresonance in the forced response of mistuned bladed disks Keith Jones and Charles Cross Propulsion Directorate, Air Force Research Laboratory, 1950 Fifth Street, Wright Patterson AFB, OH 45433-7251, USA Received 14 January 2002 Revised 2 September 2002 Abstract. Mistuning in bladed disks usually increases the forced response of the maximum responding blade leading to shortened component life in turbine engines. This paper investigates mistuning using a transfer function approach where the frequency response functions (FRFs) are described by natural frequencies and antiresonant frequencies. Using this approach, antiresonant frequencies are shown to be a critical factor in determining the maximum blade response. Two insights are gained by formulating antiresonant frequencies as the eigenvalues of reduced system matrices: 1) Mistuning a particular blade has no effect on that blade’s antiresonant frequencies. 2) Engine orders N and N/2, where N is the number of blades on the disk, tend to produce the highest maximum local response. Numerical examples are given using a spring-mass-oscillator model of a bladed disk. Pole-zero loci of mistuned bladed disks show that increased maximum blade response is often due to the damping of antiresonant frequencies. An important conclusion is that antiresonant frequencies can be arranged such that a mistuned bladed disk has a lower maximum blade response than a tuned bladed disk. Nomenclature x Displacement degree of freedom A Mistuning amplification
    [Show full text]
  • The Quartz Crystal Model and Its Frequencies
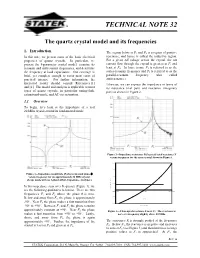
    TECHNICAL NOTE 32 The quartz crystal model and its frequencies 1. Introduction The region between F1 and F2 is a region of positive In this note, we present some of the basic electrical reactance, and hence is called the inductive region. properties of quartz crystals. In particular, we For a given AC voltage across the crystal, the net present the 4-parameter crystal model, examine its current flow through the crystal is greatest at F1 and resonant and antiresonant frequencies, and determine least at F2. In loose terms, F1 is referred to as the the frequency at load capacitance. Our coverage is series-resonant frequency and F2 is referred to as the brief, yet complete enough to cover most cases of parallel-resonant frequency (also called practical interest. For further information, the antiresonance). interested reader should consult References [1] Likewise, we can express the impedance in terms of and [2]. The model and analysis is applicable to most its resistance (real part) and reactance (imaginary types of quartz crystals, in particular tuning-fork, part) as shown in Figure 2. extensional-mode, and AT-cut resonators. 1.1 Overview To begin, let’s look at the impedance of a real 20 MHz crystal around its fundamental mode. Figure 2—Impedance resistance R (log scale) and reactance X versus frequency for the same crystal shown in Figure 1. 4,000 3,000 Figure 1—Impedance magnitude |Z| (log scale) and phase θ versus frequency for an approximately 20 MHz crystal. 2,000 (Scans made with an Agilent 4294A Impedance Analyzer.) s] 1,000 In this impedance scan over frequency (Figure 1), we Reactance X [ohm 0 see the following qualitative behavior.
    [Show full text]
  • Antiresonance in Switched Systems with Only Unstable Modes
    Antiresonance in switched systems with only unstable modes Maurizio Porri∗ Department of Mechanical and Aerospace Engineering and Department of Biomedical Engineering, New York University, Tandon School of Engineering, Brooklyn, New York 11201, USA Russell Jeter and Igor Belykhy Department of Mathematics and Statistics, Georgia State University, P.O. Box 4110, Atlanta, Georgia, 30302-410, USA (Dated: October 10, 2020) Antiresonance is a key property of dynamical systems that leads to the suppression of oscillations at select frequencies. We present the surprising example of a switched system that alternates between unstable modes, but exhibits antiresonance response for a wide range of switching frequencies. Through mathematical analysis, we elucidate the stabilization mechanism and characterize the range of antiresonant frequencies for periodic and stochastic switching. The demonstration of this new physical phenomenon opens the door for a new paradigm in the study and design of switched systems. PACS numbers: 05.45.-a, 46.40.Ff, 02.50.Ey, 45.30.+s Introduction. Switched dynamics are pervasive in the- this question by oering the rst example of a switched oretical physics, neuroscience, and engineering [1]. For system composed of unstable modes that displays a stable example, the temporal patterning of interactions within response in a nite range of switching frequencies. Our active matter systems discontinuously evolves in time system has an unstable average that hinders stability in as their comprising units change their spatial organiza- the fast-switching limit, and the instability of both of the tion [25]. Likewise, synchronization in brain networks modes hampers stability for slow-switching frequencies. emerges from sporadic, on-o synaptic interactions be- Governing equations.
    [Show full text]
  • Piezoelectric Vibration Solutions: Absorbers and Suspensions
    Piezoelectric vibration solutions : Absorbers and Suspensions Alice Aubry, Aroua Fourati, Frédéric Jean, Frédéric Mosca To cite this version: Alice Aubry, Aroua Fourati, Frédéric Jean, Frédéric Mosca. Piezoelectric vibration solutions : Absorbers and Suspensions. e-Forum Acusticum 2020, Dec 2020, Lyon, France. pp.191-194, 10.48465/fa.2020.0555. hal-03235454 HAL Id: hal-03235454 https://hal.archives-ouvertes.fr/hal-03235454 Submitted on 27 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Piezoelectric solutions: Absorbers and Suspensions Alice Aubry1 Aroua Fourati1 Frédéric Jean1 Frédéric Mosca1 1 PYTHEAS Technology, 100 Impasse des Houillières, 13590 Meyreuil, France Correspondence: [email protected] ABSTRACT Sonar systems were the first application and were developed during the first and the second World Wars by Most industrial machines present vibrations. These Paul Langevin for water communication and surveillance vibrations can lead to premature aging, mechanical failure, [1]. Nowadays, piezoelectric materials are used for
    [Show full text]
  • Comments on the Anti-Resonance Method to Measure the Circuit Con-Stants of a Coil Used As a Sensor of an Induction Magnetometer
    CORE Metadata, citation and similar papers at core.ac.uk Comments on the Anti-Resonance Method to Measure the Circuit Con-stants of a Coil Used as a Sensor of an Induction Magnetometer 著者 Ueda Hajime, Watanabe Tomiya 雑誌名 Science reports of the Tohoku University. Ser. 5, Geophysics 巻 22 号 3-4 ページ 129-136 発行年 1975-04 URL http://hdl.handle.net/10097/44723 Sci. Rep. TOhoku Univ., Ser. 5, Geophysics, Vol. 22, Nos. 3-4, pp. 129-435, 1975. Comments on the Anti—Resonance Method to Measure the Circuit Constants of a Coil Used as a Sensor of an Induction Magnetometer Technical Notes HAJIMEUEDA Departmentof Geophysics and Astronomy Universityof BritishColumbia Vancouver,Canada and TOMIYAWATANABE* OnagawaMagnetic Observatory Facultyof Science TOhokuUniversity Sendai, Japan (ReceivedJanuary 10, 1975) Abstract: In this notes, commentsare made on the theory of the antiresonance method which is often employedto measurecircuit constants of sensors of an induc- tion magnetometer. A few remarks on the practical side of this method are also made. It was found that the anti-resonancemethod is rather limited for a measure- ment of self-inductance. An alternative to the anti-resonancemethod is proposed also in this regard. 1. Introduction For a design of an induction magnetometer, it is basic to precisely measure the equivalent circuit constants of the sensor, viz, the d.c. resistance, R, self-inductance, L, and the capacitance, C. It is not difficult to measure the reistance, R. It can be measured, using a voltmeter and a d.c. power source. It is also easy to find a reliable ohmmeter on market.
    [Show full text]
  • Identification of Anti-Resonance Frequency in Buildings Based on Vibration Measurements
    1103 IDENTIFICATION OF ANTI-RESONANCE FREQUENCY IN BUILDINGS BASED ON VIBRATION MEASUREMENTS Nai-Chi LIEN1 And George C YAO2 SUMMARY A method for locating the anti-resonance frequencies (ARF) of existing buildings from modal analysis was developed in this study . The application of ARF to protect nonstructural elements in earthquake environments was proposed and found effective for shear type buildings in other studies. Most of the seismic protection methods for nonstructural elements were designed after the structures were built. It is necessary to know the ARF of building floors for seismic protection design. By using effective modal analysis and mode shape regression, the first few ARF modes in existing buildings can be found based on vibration measurements. A forced vibration test was designed to verify the sensitivity of the proposed method. The results show that a floor’s ARF can be identified only by partial vibration measurements without much error. INTRODUCTION When earthquakes attack a building, each floor vibrates according to its dynamic property and the characteristics of the ground motion. Non-structural elements attached to a floor are therefore base-excited by the floors’ vibration, which can be viewed as a filtered ground motion. The filter, in general, is a multi-DOF system and its properties are described by Frequency Response Functions (FRF). In an FRF curve, the relationship between the responses at a certain DOF when excited at other DOF is established. A typical FRF curve, as shown in Figure 1, has peaks and valleys. The peaks correspond to the natural frequencies, while the valleys correspond to the anti-resonance frequencies [Ewin, 1986].
    [Show full text]
  • Towards a Highly Sensitive Piezoelectric Nano-Mass Detection—A Model-Based Concept Study
    sensors Communication Towards a Highly Sensitive Piezoelectric Nano-Mass Detection—A Model-Based Concept Study Jens Twiefel 1,* , Anatoly Glukhovkoy 2, Sascha de Wall 2, Marc Christopher Wurz 2, Merle Sehlmeyer 3, Moritz Hitzemann 3 and Stefan Zimmermann 3 1 Institute of Dynamics and Vibration Research, Leibniz Universität Hannover, An der Universität 1 Geb. 8142, 30823 Grabsen, Germany 2 Institute of Micro Production Technology, Leibniz Universität Hannover, An der Universität 2, 30823 Grabsen, Germany; [email protected] (A.G.); [email protected] (S.d.W.); [email protected] (M.C.W.) 3 Institute of Electrical Engineering and Measurement Technology, Leibniz Universität Hannover, Appelstr. 9A, 30167 Hannover, Germany; [email protected] (M.S.); [email protected] (M.H.); [email protected] (S.Z.) * Correspondence: [email protected]; Tel.: +49-511-762-4167 Abstract: The detection of exceedingly small masses still presents a large challenge, and even though very high sensitivities have been archived, the fabrication of those setups is still difficult. In this paper, a novel approach for a co-resonant mass detector is theoretically presented, where simple fabrication is addressed in this early concept phase. To simplify the setup, longitudinal and bending vibrations were combined for the first time. The direct integration of an aluminum nitride (AlN) piezoelectric element for simultaneous excitation and sensing further simplified the setup. The feasibility of this concept is shown by a model-based approach, and the underlying parameter Citation: Twiefel, J.; Glukhovkoy, A.; de Wall, S.; Wurz, M.C.; Sehlmeyer, dependencies are presented with an equivalent model.
    [Show full text]