Predicting New Workload Or CPU Performance by Analyzing Public Datasets
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Memory Centric Characterization and Analysis of SPEC CPU2017 Suite
Session 11: Performance Analysis and Simulation ICPE ’19, April 7–11, 2019, Mumbai, India Memory Centric Characterization and Analysis of SPEC CPU2017 Suite Sarabjeet Singh Manu Awasthi [email protected] [email protected] Ashoka University Ashoka University ABSTRACT These benchmarks have become the standard for any researcher or In this paper, we provide a comprehensive, memory-centric charac- commercial entity wishing to benchmark their architecture or for terization of the SPEC CPU2017 benchmark suite, using a number of exploring new designs. mechanisms including dynamic binary instrumentation, measure- The latest offering of SPEC CPU suite, SPEC CPU2017, was re- ments on native hardware using hardware performance counters leased in June 2017 [8]. SPEC CPU2017 retains a number of bench- and operating system based tools. marks from previous iterations but has also added many new ones We present a number of results including working set sizes, mem- to reflect the changing nature of applications. Some recent stud- ory capacity consumption and memory bandwidth utilization of ies [21, 24] have already started characterizing the behavior of various workloads. Our experiments reveal that, on the x86_64 ISA, SPEC CPU2017 applications, looking for potential optimizations to SPEC CPU2017 workloads execute a significant number of mem- system architectures. ory related instructions, with approximately 50% of all dynamic In recent years the memory hierarchy, from the caches, all the instructions requiring memory accesses. We also show that there is way to main memory, has become a first class citizen of computer a large variation in the memory footprint and bandwidth utilization system design. -

Overview of the SPEC Benchmarks
9 Overview of the SPEC Benchmarks Kaivalya M. Dixit IBM Corporation “The reputation of current benchmarketing claims regarding system performance is on par with the promises made by politicians during elections.” Standard Performance Evaluation Corporation (SPEC) was founded in October, 1988, by Apollo, Hewlett-Packard,MIPS Computer Systems and SUN Microsystems in cooperation with E. E. Times. SPEC is a nonprofit consortium of 22 major computer vendors whose common goals are “to provide the industry with a realistic yardstick to measure the performance of advanced computer systems” and to educate consumers about the performance of vendors’ products. SPEC creates, maintains, distributes, and endorses a standardized set of application-oriented programs to be used as benchmarks. 489 490 CHAPTER 9 Overview of the SPEC Benchmarks 9.1 Historical Perspective Traditional benchmarks have failed to characterize the system performance of modern computer systems. Some of those benchmarks measure component-level performance, and some of the measurements are routinely published as system performance. Historically, vendors have characterized the performances of their systems in a variety of confusing metrics. In part, the confusion is due to a lack of credible performance information, agreement, and leadership among competing vendors. Many vendors characterize system performance in millions of instructions per second (MIPS) and millions of floating-point operations per second (MFLOPS). All instructions, however, are not equal. Since CISC machine instructions usually accomplish a lot more than those of RISC machines, comparing the instructions of a CISC machine and a RISC machine is similar to comparing Latin and Greek. 9.1.1 Simple CPU Benchmarks Truth in benchmarking is an oxymoron because vendors use benchmarks for marketing purposes. -

Oracle Corporation: SPARC T7-1
SPEC CINT2006 Result spec Copyright 2006-2015 Standard Performance Evaluation Corporation Oracle Corporation SPECint_rate2006 = 1200 SPARC T7-1 SPECint_rate_base2006 = 1120 CPU2006 license: 6 Test date: Oct-2015 Test sponsor: Oracle Corporation Hardware Availability: Oct-2015 Tested by: Oracle Corporation Software Availability: Oct-2015 Copies 0 300 600 900 1200 1600 2000 2400 2800 3200 3600 4000 4400 4800 5200 5600 6000 6400 6800 7600 1100 400.perlbench 192 224 1040 675 401.bzip2 256 224 666 875 403.gcc 160 224 720 1380 429.mcf 128 224 1160 1190 445.gobmk 256 224 1120 854 456.hmmer 96 224 813 1020 458.sjeng 192 224 988 7550 462.libquantum 416 224 7330 1190 464.h264ref 256 224 1150 956 471.omnetpp 255 224 885 986 473.astar 416 224 862 1180 483.xalancbmk 256 224 1140 SPECint_rate_base2006 = 1120 SPECint_rate2006 = 1200 Hardware Software CPU Name: SPARC M7 Operating System: Oracle Solaris 11.3 CPU Characteristics: Compiler: C/C++/Fortran: Version 12.4 of Oracle Solaris CPU MHz: 4133 Studio, FPU: Integrated 4/15 Patch Set CPU(s) enabled: 32 cores, 1 chip, 32 cores/chip, 8 threads/core Auto Parallel: No CPU(s) orderable: 1 chip File System: zfs Primary Cache: 16 KB I + 16 KB D on chip per core System State: Default Secondary Cache: 2 MB I on chip per chip (256 KB / 4 cores); Base Pointers: 32-bit 4 MB D on chip per chip (256 KB / 2 cores) Peak Pointers: 32-bit L3 Cache: 64 MB I+D on chip per chip (8 MB / 4 cores) Other Software: None Other Cache: None Memory: 512 GB (16 x 32 GB 4Rx4 PC4-2133P-L) Disk Subsystem: 732 GB, 4 x 400 GB SAS SSD -

Poweredge R940 (Intel Xeon Gold 5122, 3.60 Ghz) Specint Rate Base2006 = 1080 CPU2006 License: 55 Test Date: Jun-2017 Test Sponsor: Dell Inc
SPEC CINT2006 Result spec Copyright 2006-2017 Standard Performance Evaluation Corporation Dell Inc. SPECint_rate2006 = 1150 PowerEdge R940 (Intel Xeon Gold 5122, 3.60 GHz) SPECint_rate_base2006 = 1080 CPU2006 license: 55 Test date: Jun-2017 Test sponsor: Dell Inc. Hardware Availability: Jul-2017 Tested by: Dell Inc. Software Availability: Nov-2016 Copies 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000 12000 13000 14000 15000 16000 18000 917 400.perlbench 32 32 762 521 401.bzip2 32 32 487 808 403.gcc 32 32 802 1480 429.mcf 32 624 445.gobmk 32 2010 456.hmmer 32 32 1530 710 458.sjeng 32 32 658 17700 462.libquantum 32 1170 464.h264ref 32 32 1130 554 471.omnetpp 32 32 509 614 473.astar 32 1430 483.xalancbmk 32 SPECint_rate_base2006 = 1080 SPECint_rate2006 = 1150 Hardware Software CPU Name: Intel Xeon Gold 5122 Operating System: SUSE Linux Enterprise Server 12 SP2 CPU Characteristics: Intel Turbo Boost Technology up to 3.70 GHz 4.4.21-69-default CPU MHz: 3600 Compiler: C/C++: Version 17.0.3.191 of Intel C/C++ FPU: Integrated Compiler for Linux CPU(s) enabled: 16 cores, 4 chips, 4 cores/chip, 2 threads/core Auto Parallel: Yes CPU(s) orderable: 2,4 chip File System: xfs Primary Cache: 32 KB I + 32 KB D on chip per core System State: Run level 3 (multi-user) Secondary Cache: 1 MB I+D on chip per core Base Pointers: 32-bit L3 Cache: 16.5 MB I+D on chip per chip Peak Pointers: 32/64-bit Other Cache: None Other Software: Microquill SmartHeap V10.2 Memory: 768 GB (48 x 16 GB 2Rx8 PC4-2666V-R) Disk Subsystem: 1 x 960 GB SATA SSD Other Hardware: None Standard Performance Evaluation Corporation [email protected] Page 1 http://www.spec.org/ SPEC CINT2006 Result spec Copyright 2006-2017 Standard Performance Evaluation Corporation Dell Inc. -

IBM Power Systems Performance Report Apr 13, 2021
IBM Power Performance Report Power7 to Power10 September 8, 2021 Table of Contents 3 Introduction to Performance of IBM UNIX, IBM i, and Linux Operating System Servers 4 Section 1 – SPEC® CPU Benchmark Performance 4 Section 1a – Linux Multi-user SPEC® CPU2017 Performance (Power10) 4 Section 1b – Linux Multi-user SPEC® CPU2017 Performance (Power9) 4 Section 1c – AIX Multi-user SPEC® CPU2006 Performance (Power7, Power7+, Power8) 5 Section 1d – Linux Multi-user SPEC® CPU2006 Performance (Power7, Power7+, Power8) 6 Section 2 – AIX Multi-user Performance (rPerf) 6 Section 2a – AIX Multi-user Performance (Power8, Power9 and Power10) 9 Section 2b – AIX Multi-user Performance (Power9) in Non-default Processor Power Mode Setting 9 Section 2c – AIX Multi-user Performance (Power7 and Power7+) 13 Section 2d – AIX Capacity Upgrade on Demand Relative Performance Guidelines (Power8) 15 Section 2e – AIX Capacity Upgrade on Demand Relative Performance Guidelines (Power7 and Power7+) 20 Section 3 – CPW Benchmark Performance 19 Section 3a – CPW Benchmark Performance (Power8, Power9 and Power10) 22 Section 3b – CPW Benchmark Performance (Power7 and Power7+) 25 Section 4 – SPECjbb®2015 Benchmark Performance 25 Section 4a – SPECjbb®2015 Benchmark Performance (Power9) 25 Section 4b – SPECjbb®2015 Benchmark Performance (Power8) 25 Section 5 – AIX SAP® Standard Application Benchmark Performance 25 Section 5a – SAP® Sales and Distribution (SD) 2-Tier – AIX (Power7 to Power8) 26 Section 5b – SAP® Sales and Distribution (SD) 2-Tier – Linux on Power (Power7 to Power7+) -

QSCORES: Trading Dark Silicon for Scalable Energy Efficiency With
QSCORES: Trading Dark Silicon for Scalable Energy Efficiency with Quasi-Specific Cores Ganesh Venkatesh+, Jack Sampson, Nathan Goulding-Hotta, Sravanthi Kota Venkata+, Michael Bedford Taylor and Steven Swanson http://greendroid.org Department of Computer Science and Engineering University of California, San Diego ABSTRACT General Terms Transistor density continues to increase exponentially, but power Design, Experimentation, Measurement dissipation per transistor is improving only slightly with each gen- eration of Moore’s law. Given the constant chip-level power bud- Keywords gets, this exponentially decreases the percentage of transistors that QSCORE, Conservation Core, Merging, Dark Silicon, Utilization can switch at full frequency with each technology generation. Hence, Wall, Heterogeneous Many-Core, Specialization while the transistor budget continues to increase exponentially, the power budget has become the dominant limiting factor in processor design. In this regime, utilizing transistors to design specialized 1. INTRODUCTION cores that optimize energy-per-computation becomes an effective Although transistor density continues to scale, nearly constant approach to improve system performance. per-transistor power and fixed chip-level power budget place tight To trade transistors for energy efficiency in a scalable manner, we constraints on how much of a chip can be active at full frequency at propose Quasi-specific Cores, or QSCORES, specialized processors one time. Hence, as transistor density increases with each process capable of executing multiple general-purpose computations while generation, so does the fraction of the chip that must be under- providing an order of magnitude more energy efficiency than a clocked or under-utilized because of power concerns [27]. Re- general-purpose processor. The QSCORE design flow is based on searchers have termed these passive expanses of silicon area dark the insight that similar code patterns exist within and across appli- silicon [14, 11, 15, 17, 21]. -

(SLB) Predictor: a Compiler Assisted Branch Prediction for Data Dependent Branches
Store-Load-Branch (SLB) Predictor: A Compiler Assisted Branch Prediction for Data Dependent Branches M. Umar Farooq Khubaib Lizy K. John Department of Electrical and Computer Engineering The University of Texas at Austin [email protected], [email protected], [email protected] Abstract This work is based on the following observation: Hard- to-predict data-dependent branches are commonly associ- Data-dependent branches constitute single biggest ated with program data structures such as arrays, linked source of remaining branch mispredictions. Typically, lists, trees etc., and follow store-load-branch execution se- data-dependent branches are associated with program quence similar to one shown in listing 1. A set of memory data structures, and follow store-load-branch execution se- locations is written while building and updating the data quence. A set of memory locations is written at an earlier structure (line 2, listing 1). During data structure traver- point in a program. Later, these locations are read, and sal, these locations are read, and used for evaluating branch used for evaluating branch condition. Branch outcome de- condition (line 7, listing 1). pends on data values stored in data structure, which, typi- 52 50 53 cally do not have repeatable pattern. Therefore, in addition 35 Gshare to history-based dynamic predictor, we need a different kind 30 YAGS BiMode of predictor for handling such branches. TAGE 25 This paper presents Store-Load-Branch (SLB) predic- 20 tor; a compiler-assisted dynamic branch prediction scheme for data-dependent direct and indirect branches. For ev- 15 ery data-dependent branch, compiler identifies store in- 10 5 structions that modify the data structure associated with Mispredictions per 1K instructions the branch. -

Benchmarking-HOWTO.Pdf
Linux Benchmarking HOWTO Linux Benchmarking HOWTO Table of Contents Linux Benchmarking HOWTO.........................................................................................................................1 by André D. Balsa, [email protected] ..............................................................................................1 1.Introduction ..........................................................................................................................................1 2.Benchmarking procedures and interpretation of results.......................................................................1 3.The Linux Benchmarking Toolkit (LBT).............................................................................................1 4.Example run and results........................................................................................................................2 5.Pitfalls and caveats of benchmarking ..................................................................................................2 6.FAQ .....................................................................................................................................................2 7.Copyright, acknowledgments and miscellaneous.................................................................................2 1.Introduction ..........................................................................................................................................2 1.1 Why is benchmarking so important ? ...............................................................................................3 -

The Benefits of Hardware-Software Co-Design/Convergence for Large- Scale Enterprise Workloads
The Benefits of Hardware-Software Co-Design/Convergence for Large- Scale Enterprise Workloads Michael Palmeter Sr. Director Oracle Systems Engineering Copyright © 2016, Oracle and/or its affiliates. All rights reserved. | Required Benchmark Disclosure Statement Must be in SPARC S7 or M7 Presentations with Benchmark Results •Additional Info: http://blogs.oracle.com/bestperf •Copyright 2017, Oracle &/or its affiliates. All rights reserved. Oracle & Java are registered trademarks of Oracle &/or its affiliates. Other names may be trademarks of their respective owners •SPEC and the benchmark name SPECjEnterprise are registered trademarks of the Standard Performance Evaluation Corporation. Results from www.spec.org as of 10/25/2017. SPARC T7-1, 25,818.85 SPECjEnterprise2010 EjOPS (unsecure); SPARC T7-1, 25,093.06 SPECjEnterprise2010 EjOPS (secure); Oracle Server X5-2, 21,504.30 SPECjEnterprise2010 EjOPS (unsecure); IBM Power S824, 22,543.34 SPECjEnterprise2010 EjOPS (unsecure); IBM x3650 M5, 19,282.14 SPECjEnterprise2010 EjOPS (unsecure). •SPEC and the benchmark name SPECvirt_sc are registered trademarks of the Standard Performance Evaluation Corporation. Results from www.spec.org as of 10/25/2017. SPARC T7-2, SPECvirt_sc2013 3026@168 VMs; HP DL580 Gen9, SPECvirt_sc2013 3020@168 VMs; Lenovo x3850 X6; SPECvirt_sc2013 2655@147 VMs; Huawei FusionServer RH2288H V3, SPECvirt_sc2013 1616@95 VMs; HP ProLiant DL360 Gen9, SPECvirt_sc2013 1614@95 VMs; IBM Power S824, SPECvirt_sc2013 1371@79 VMs. •SPEC and the benchmark names SPECfp and SPECint are registered trademarks of the Standard Performance Evaluation Corporation. Results as of October 25, 2017 from www.spec.org and this report. 1 chip results SPARC T7-1: 1200 SPECint_rate2006, 1120 SPECint_rate_base2006, 832 SPECfp_rate2006, 801 SPECfp_rate_base2006; SPARC T5-1B: 489 SPECint_rate2006, 440 SPECint_rate_base2006, 369 SPECfp_rate2006, 350 SPECfp_rate_base2006; Fujitsu SPARC M10-4S: 546 SPECint_rate2006, 479 SPECint_rate_base2006, 462 SPECfp_rate2006, 418 SPECfp_rate_base2006. -

Proliant DL380 Gen10
SPEC CINT2006 Result spec Copyright 2006-2017 Standard Performance Evaluation Corporation Hewlett Packard Enterprise (Test Sponsor: HPE) SPECint 2006 = Not Run ProLiant DL380 Gen10 (2.50 GHz, Intel Xeon Platinum 8180) SPECint_base2006 = 81.0 CPU2006 license: 3 Test date: Jun-2017 Test sponsor: HPE Hardware Availability: Sep-2017 Tested by: HPE Software Availability: May-2017 0 300 600 900 1300 1700 2100 2500 2900 3300 3700 4100 4500 4900 5300 5700 6100 6500 6900 7300 7700 8100 8500 9300 400.perlbench 47.7 401.bzip229.3 403.gcc 46.6 429.mcf 82.9 445.gobmk34.6 456.hmmer 97.5 458.sjeng38.3 462.libquantum 9250 464.h264ref 70.3 471.omnetpp 51.3 473.astar40.2 483.xalancbmk 85.1 SPECint_base2006 = 81.0 Hardware Software CPU Name: Intel Xeon Platinum 8180 Operating System: Red Hat Enterprise Linux Server release 7.3 CPU Characteristics: Intel Turbo Boost Technology up to 3.80 GHz (Maipo) CPU MHz: 2500 Kernel 3.10.0-514.el7.x86_64 FPU: Integrated Compiler: C/C++: Version 17.0.4.196 of Intel C/C++ CPU(s) enabled: 28 cores, 1 chip, 28 cores/chip Compiler for Linux CPU(s) orderable: 1,2 chip(s) Auto Parallel: Yes Primary Cache: 32 KB I + 32 KB D on chip per core File System: xfs Secondary Cache: 1 MB I+D on chip per core System State: Run level 3 (multi-user) L3 Cache: 38.5 MB I+D on chip per chip Base Pointers: 32/64-bit Other Cache: None Peak Pointers: 32/64-bit Memory: 96 GB (12 x 8 GB 2Rx8 PC4-2666V-R) Other Software: Microquill SmartHeap V10.2 Disk Subsystem: 1 x 450 GB SATA SSD, RAID 0 Other Hardware: None Standard Performance Evaluation -

2.70 Ghz, Intel Xeon Platinum 8168
SPEC CINT2006 Result spec Copyright 2006-2018 Standard Performance Evaluation Corporation Hewlett Packard Enterprise (Test Sponsor: HPE) SPECint _rate2006 = Not Run Synergy 480 Gen10 (2.70 GHz, Intel Xeon Platinum 8168) SPECint_rate_base2006 = 2460 CPU2006 license: 3 Test date: Dec-2017 Test sponsor: HPE Hardware Availability: Oct-2017 Tested by: HPE Software Availability: Sep-2017 Copies 0 2000 4000 6000 8000 11000 14000 17000 20000 23000 26000 29000 32000 35000 38000 41000 46000 1910 400.perlbench 96 1110 401.bzip2 96 1660 403.gcc 96 2970 429.mcf 96 1680 445.gobmk 96 3430 456.hmmer 96 1770 458.sjeng 96 45500 462.libquantum 96 2910 464.h264ref 96 1090 471.omnetpp 96 1270 473.astar 96 2470 483.xalancbmk 96 SPECint_rate_base2006 = 2460 Hardware Software CPU Name: Intel Xeon Platinum 8168 Operating System: SUSE Linux Enterprise Server 12 (x86_64) SP2 CPU Characteristics: Intel Turbo Boost Technology up to 3.70 GHz Kernel 4.4.21-69-default CPU MHz: 2700 Compiler: C/C++: Version 18.0.0.128 of Intel C/C++ FPU: Integrated Compiler for Linux CPU(s) enabled: 48 cores, 2 chips, 24 cores/chip, 2 threads/core Auto Parallel: No CPU(s) orderable: 1, 2 chip(s) File System: xfs Primary Cache: 32 KB I + 32 KB D on chip per core System State: Run level 3 (multi-user) Secondary Cache: 1 MB I+D on chip per core Base Pointers: 32-bit L3 Cache: 33 MB I+D on chip per chip Peak Pointers: Not Applicable Other Cache: None Other Software: Microquill SmartHeap V10.2 Memory: 384 GB (24 x 16 GB 2Rx8 PC4-2666V-R) Disk Subsystem: 1 x 480 GB SATA SSD, RAID 0 Other -
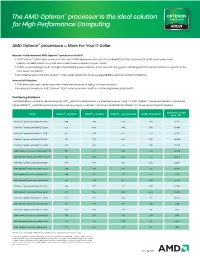
The AMD Opteron™ Processor Is the Ideal Solution for High Performance Computing
The AMD Opteron™ processor is the ideal solution for High Performance Computing AMD Opteron™ processors = More For Your IT Dollar Reasons to Recommend AMD Opteron™ processors for HPC: • AMD Opteron™ 6200 Series processors offer up to 34% lower processor price/theoretical GFLOP than Intel Xeon E5-2600 Series processors. Making it an ideal solution for public sector and university research opportunities.1 • AMD has been helping to build the highest performing supercomputers in the world for many years, including 24 of the 100 most powerful systems in the most recent Top 500 list.2 • Consistency across the AMD Opteron™ 6000 series processors for easy upgradeability and backwards compatibility How to Sell/Position: • AMD dedicated cores deliver consistent thread performance for highly scalable workloads. • 4 memory channels per AMD Opteron™ 6200 Series processor results in outstanding memory bandwidth. Positioning Guidance The table below is sorted by descending SPECint®_rate2006 performance. For example, a server using 2 x AMD Opteron™ processors Model 6274 provides higher SPECint®_rate2006 performance than a server using 2 x Intel Xeon™ processor Model E5-2640 AND has a lower total processor 1kU price. ® 3 ® ® Total Processor 1kU Model SPECint _ rate2006 SPECfp _ rate2006 SPECint _ rate_base2006 GFLOPs (Theoretical) Price - 2P* Intel Xeon™ processor Model E5-2690 705 510 671 371 $4,114 Intel Xeon™ processor Model E5-2680 666 494 640 346 $3,446 Intel Xeon™ processor Model E5-2670 647 486 622 333 $3,104 Intel Xeon™ processor Model E5-2665