Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Systematic Review and Meta-Analysis of X-Ray Detective
Wang et al. BMC Musculoskeletal Disorders (2019) 20:78 https://doi.org/10.1186/s12891-019-2461-z RESEARCHARTICLE Open Access The systematic review and meta-analysis of X-ray detective rate of Kashin-Beck disease from 1992 to 2016 Xi Wang1,2†, Yujie Ning1†, Amin Liu1, Xin Qi1, Meidan Liu1, Pan Zhang1 and Xiong Guo1* Abstract Background: Kashin-Beck disease (KBD) is a serious human endemic chronic osteochondral disease. However, quantitative syntheses of X-ray detective rate studies for KBD are rare. We performed an initial systematic review and meta-analysis to assess the X-ray detective rate of KBD in China. Methods: For this systematic review and meta-analysis, we searched five databases (PubMed, Web of Science, Chinese National Knowledge Infrastructure (CNKI), WanFang Data and the China Science and Technology Journal Database (VIP))using a comprehensive search strategy to identify studies of KBD X-ray detective rate in China that were published from database inception to January 13, 2018. The X-ray detective rate of KBD was determined via an analysis of published studies using a random effect meta-analysis with the proportions approach. Subgroup analysis and meta- regression were used to explore heterogeneity, and study quality was assessed using the risk of bias tool. Results: A total of 53 studies involving 14,039 samples with X-ray detective rate in 163,340 observations in total were included in this meta-analysis. These studies were geographically diverse (3 endemic areas). The pooled overall X-ray detective rate for KBD was 11% (95%CI,8–15%;Z = 13.14; p < 0.001). -

Environmental Impact Assessment Report of Shaanxi Small Towns
E4461 V1 REV EIA Report of Shaanxi Zhongsheng Assessment Certificate Category: Grade A SZSHPS-2013-075 Assessment Certificate No.:3607 Public Disclosure Authorized Environmental Impact Assessment Report of Shaanxi Small Towns Infrastructure Project with World Bank Loan Public Disclosure Authorized (Draft for review) Public Disclosure Authorized Entrusted by: Foreign Loan Supporting Project Management Office of Shaanxi Province Assessed by: Shaanxi Zhongsheng Environmental Technologies Development Co., Ltd. March 2014 Public Disclosure Authorized Content 0 Foreword ................................................................................................................................................. 1 0.1 Project Background ................................................................................................................. 1 0.2 Assessment Category .............................................................................................................. 2 0.4 Project Feature ....................................................................................................................... 3 0.5 Major Environmental Problems Concerned in Environmental Assessment ......................... 4 0.6 Major Conclusion in Report .................................................................................................... 4 0.7 Acknowledgement .................................................................................................................. 4 1 General Provisions ................................................................................................................................. -

Is It the Appropriate Time to Stop Applying Selenium Enriched Salt in Kashin-Beck Disease Areas in China?
Nutrients 2015, 7, 6195-6212; doi:10.3390/nu7085276 OPEN ACCESS nutrients ISSN 2072-6643 www.mdpi.com/journal/nutrients Article Is It the Appropriate Time to Stop Applying Selenium Enriched Salt in Kashin-Beck Disease Areas in China? Yujie Ning :, Xi Wang :, Sen Wang, Feng Zhang, Lianhe Zhang, Yanxia Lei and Xiong Guo * School of Public Health, Health Science Center, Xi’an Jiaotong University, Key Laboratory of Trace Elements and Endemic Diseases, National Health and Family Planning Commission, Xi’an, Shaanxi 710061, China; E-Mails: [email protected] (Y.N.); [email protected] (X.W.); [email protected] (S.W.); [email protected] (F.Z.); [email protected] (L.Z.); [email protected] (Y.L.) : These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +86-029-82655091; Fax: +86-029-82655032. Received: 5 June 2015 / Accepted: 20 July 2015 / Published: 28 July 2015 Abstract: We aimed to identify significant factors of selenium (Se) nutrition of children in Kashin-Beck disease (KBD) endemic areas and non-KBD area in Shaanxi Province for providing evidence of whether it is the time to stop applying Se-enriched salt in KBD areas. A cross-sectional study contained 368 stratified randomly selected children aged 4–14 years was conducted with 24-h retrospective questionnaire based on a pre-investigation. Food and hair samples were collected and had Se contents determined with hydride generation atomic fluorescence spectrometry. Average hair Se content of 349.0 ˘ 60.2 ng/g in KBD-endemic counties was significantly lower than 374.1 ˘ 47.0 ng/g in non-KBD counties. -
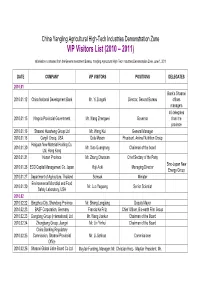
VIP Visitors List (2010 – 2011)
China Yangling Agricultural High-Tech Industries Demonstration Zone VIP Visitors List (2010 – 2011) Information is obtained from the General Investment Bureau, Yangling Agricultural High-Tech Industries Demonstration Zone, June 1, 2011 DATE COMPANY VIP VISITORS POSITIONS DELEGATES 2010.01 Bank's Shaanxi 2010.01.12 China National Development Bank Mr. Yi Zongshi Director, Second Bureau offices managers 40 delegates 2010.01.15 Ningxia Provincial Government Mr. Wang Zhengwei Governor from the province 2010.01.16 Shaanxi Huasheng Group Ltd Mr. Wang Kui General Manager 2010.01.18 Cargill Group, USA Dula Muson President, Animal Nutrition Group Haiguan New Material Holding Co. 2010.01.20 Mr. Xiao Guangrong Chairman of the board Ltd, Hong Kong 2010.01.21 Hunan Province Mr. Zhang Chunxian Chief Sectary of the Party Sino-Japan New 2010.01.26 ECO Capital Management Co. Japan Koji Aoki Managing Director Energy Group 2010.01.27 Department of Agriculture, Thailand Somsak Minister Environmental Microbial and Food 2010.01.30 Mr. Luo Yaguang Senior Scientist Safety Laboratory, USA 2010.02 2010.02.22 Bingzhou City, Shandong Province Mr. Shang Longjiang Deputy Mayor 2010.02.23 BASF Corporation, Germany Francis Ka Fritz Chief Officer, Bio-earth Film Group 2010.02.23 Dongfang Group (International) Ltd Mr. Wang Jiankun Chairman of the Board 2010.02.24 Zhengbang Group, Jiangxi Mr. Lin Yinhui Chairman of the Board China Banking Regulatory 2010.02.25 Commission, Shaanxi Provincial Mr. Li Jianhua Commissioner Office 2010.02.26 Shaanxi Global Jiahe Board Co Ltd Mayfair Funding, Manager: Mr. Christian Herz,Mayfair President: Mr. Rainer Kutzner (Germany), PBH Ltd President: Mr. -

Effects of Formulated Fertilizer, Irrigation and Varieties on Wheat Yield in Shaanxi China
Available online www.jocpr.com Journal of Chemical and Pharmaceutical Research, 2014, 6(7):1124-1129 ISSN : 0975-7384 Research Article CODEN(USA) : JCPRC5 Effects of formulated fertilizer, irrigation and varieties on wheat yield in Shaanxi China Xiaoying Wang1, Yanan Tong1,2*, Pengcheng Gao1, Fen Liu1, Yimin Gao1, Zuoping Zhao1 and Yan Pang1 1College of Resources and Environment, Northwest A&F University, Yangling, Shaanxi, China 2Key Laboratory of Plant Nutrition and Agricultural Environment in Northwest, Ministry of Agriculture, Yangling, Shaanxi, China _____________________________________________________________________________________________ ABSTRACT In order to study the effects of formulated fertilization, irrigation and different varieties on crop yields and farmer’s income, this research used household survey data and demonstration test data of formulated fertilization, which was collected from the project of soil testing and formulated fertilization in Shaanxi province from 2007 to 2011. For analysis, there were a total of 53 counties in the sample. The results show that in Weibei, Guanzhong and Qin-Ba regions, compared with conventional fertilization, formulated fertilization decreased nitrogen (N) fertilizer rates by 31.92%, 12.59% and 10.13% respectively, decreased phosphate (P2O5) fertilizer rates by 20.44%, 2.10% and 26.19% respectively, increased potassium (K2O) fertilizer rates by 105.98%, 193.99% and 382.58% respectively. The yields of wheat improved 330 kg ha-1, 403 kg ha-1 and 738 kg ha-1, the yield increase rates were 7.73%, 6.26% and 19.71%, the average profits increased about 906 yuan ha-1, 689 yuan ha-1 and 1423 yuan ha-1 respectively in the three regions. In addition, the average yields were higher up to 19.07%, 14.96% and 17.76% respectively when irrigation had been used than without, and it was not the most productive varieties that were the most grown in the three regions. -

Minimum Wage Standards in China August 11, 2020
Minimum Wage Standards in China August 11, 2020 Contents Heilongjiang ................................................................................................................................................. 3 Jilin ............................................................................................................................................................... 3 Liaoning ........................................................................................................................................................ 4 Inner Mongolia Autonomous Region ........................................................................................................... 7 Beijing......................................................................................................................................................... 10 Hebei ........................................................................................................................................................... 11 Henan .......................................................................................................................................................... 13 Shandong .................................................................................................................................................... 14 Shanxi ......................................................................................................................................................... 16 Shaanxi ...................................................................................................................................................... -

Shanxi WLAN Hotspots 1/23
Shanxi WLAN hotspots NO. SSID Location_Name Location_Type Location_Address City Province 1 ChinaNet Xi'an Beilin Qu friendship distance tea lounge bar entertainment bars Friendship Road No. 260 on the 1st Deputy Xi'An shaanxi 2 ChinaNet Xi'an Aidi Food Management Co., Ltd. entertainment bars Friendship Road 127, creativity Xi'An shaanxi 3 ChinaNet Xi'an Lianhu District Run-Xuan Teahouse entertainment bars Friendship Road 127, 53, deputy Xi'An shaanxi 4 ChinaNet Yanta District in Xi'an Ziwei Wang waterfall poor artists entertainment bars E-249, all the way Xi'An shaanxi Xi'an high-tech zones love Qindao Art of Living Museum 5 ChinaNet entertainment bars E-foot Street North, 103 East Street, I love Qindao cafe Xi'An shaanxi coffee bad language 6 ChinaNet Yanta District in Xi'an Ming Shi-language music coffee tea entertainment bars Han Guang Ming-shi, 100 South Lok coffee language tea Xi'An shaanxi 7 ChinaNet Xi'an Lianhu District Duoji Cafe entertainment bars Labor South on the 17th to pay on the 22nd on the 23rd Xi'An shaanxi 8 ChinaNet Xian Ou goods Food Co., Ltd. entertainment bars Road work on the 17th to pay on the 12th Xi'An shaanxi 9 ChinaNet Henrik Business Hotel hotels Auspicious Road Xi'An shaanxi 10 ChinaNet Xian Ming Jue Dining Entertainment Co., Ltd. entertainment bars High road on the 23rd Xi'An shaanxi 11 ChinaNet Tang Yan Tang Ruins Park Plaza Road entertainment bars Tang Yan Road Xi'An shaanxi 12 ChinaNet HSBC coffee entertainment bars Technology Road Xi'An shaanxi 13 ChinaNet Xi'an high-tech love Investment Group Co., Ltd. -

Study of Road Landscape Design at Portal Space of Small Towns in Guanzhong
Send Orders for Reprints to [email protected] 92 The Open Construction and Building Technology Journal, 2015, 9, 92-98 Open Access Study of Road Landscape Design at Portal Space of Small Towns in Guanzhong# Quanhua Hou* and Wenhui Wang School of Architecture, Chang' an University, Xi'an 710061, China Abstract: To further study the effects of public service facilities on the land use intensity at regulatory planning level and enhance the scientific determination of land use intensity, this paper expounds the influence mechanism and factors of the public service facilities on land use intensity in regulatory planning, and conducts quantitative evaluation of the influence factors through theoretical analysis, mathematical analysis and analytic hierarchy process etc. The results show that the in- fluence mechanism of public service facilities on the land use intensity goes throughout all three levels of regulatory plan- ning. Different characteristics of public service facilities on each level determine their different influence factors and take effect on the land use intensity index of the corresponding level, thus affecting the determination of the block floor area ratio. Based on this, this paper proposes a method to determine the land use intensity in regulatory planning under the re- striction of public service facilities and completes the test in practice, which may provide a reference for determining the land use intensity in regulatory planning. Keywords: Impact assessment, land use intensity, public service facilities, regulatory -

Sponsored by the Society for Asian Art
Arts of Asia Lecture Series Spring 2019 The Architecture of Asia: From Baghdad to Beijing, Kabul to Kyoto and Tehran to Tokyo Sponsored by The Society for Asian Art East Asian Architecture in the 5th-10th Centuries Nancy S. Steinhardt, University of Pennsylvania February 8, 2019 MAJOR DYNASTIES AND CAPITALS OF CHINA Three Kingdoms Wei (220-264), capital at Ye, Hebei Shu (-Han) (221-263), capital at Chengdu Wu (222-280), capital at Jianye (Nanjing) Wei-Jin (220-317) only in North Jin dynasty (265-420) Western Jin (281-316) CHINA IS UNIFIED Eastern Jin (317-420) Six Dynasties (220-589) Western Jin, Eastern Jin, Liu-Song, Southern Qi, Liang, Chen Capital at Jiankang (Nanjing) beginning in Eastern Jin Sixteen States (304-439) only in the North Northern Dynasties (386-534) Northern Wei (386-534), capitals at Shengle (398-, Pingcheng (Datong) (-492), and Luoyang (493-534) Eastern Wei (534-550), capital at Ye Western Wei (535-557), capital at Chang’an Northern Qi (550-577), capital at Ye and auxiliary capital at Taiyuan Northern Zhou (557-581), capital at Chang'an Southern Dynasties (420-589), all capitals in Jiankang (Nanjing) Liu-Song (420-479) Southern Qi (479-502) Liang (502-557) Chen (557-589) Sui Dynasty (581/89-618), capitals in Chang’an and Luoyang Tang Dynasty (618-907), capitals in Chang’an and Luoyang PERIODS OF KOREAN HISTORY Koguryo/Goguryeo (37 BCE – CE 668), capitals in P’yongyang and Jian Paekche/Baekje (18 BCE – CE 660), capital in Puyo/Buyeo Silla (57 BCE – CE 668), capital in Kyongju/Gyeongju Northern and Southern Dynasties -

World Bank Document
Procurement Plan I. General Public Disclosure Authorized 1. Bank’s approval Date of the procurement Plan [Original: December16, 2016: 1stRevision: June 28, 2017, 2nd Revision: August 18, 2017, 3rd Revision: August 14, 2018, 4th Revision: August 23, 2018 for Mizhi, 5th Revision: August 30 for Yanchang;6th Revision: September 5, 2018 for Heyang, Longxian and Baishui; 7th Revision: December 4, 2018 for Yichuan; 8th Revision: April 4, 2019; 9th Revision: March 16, 2020; 10th Revision: May 18, 2020] 2. Date of General Procurement Notice: Jan 24, 2017 3. Period covered by this procurement plan: 2016-2022 II. Goods and Works and non-consulting services. Public Disclosure Authorized 1. Prior Review Threshold: Procurement Decisions subject to Prior Review by the Bank as stated in Appendix 1 to the Guidelines for Procurement: Procurement Method Prior Review Threshold Comments US$ 1. ICB and LIB (Goods) Above US$ 10million All 2. NCB (Goods) Above US$ 2million All 3. ICB (Works) Above US$ 40 million All 4. NCB (Works) Above US$ 10 million All 5. (Non-Consultant Services) Above US$ 2million All [Add other methods if necessary] Public Disclosure Authorized 2. Prequalification. Bidders for _Not applicable_ shall be prequalified in accordance with the provisions of paragraphs 2.9 and 2.10 of the Guidelines. 3. Proposed Procedures for CDD Components (as per paragraph. 3.17 of the Guidelines: [Yes, in procurement manual] 4. Reference to (if any) Project Operational/Procurement Manual: Yes 5. Any Other Special Procurement Arrangements: no 6. Summary of the Procurement Packages planned during the first 18 months after project effectiveness (including those that are subject to retroactive financing and advanced procurement) Public Disclosure Authorized [List the Packages which require Bank’s prior review first and then the other packages] 1 2 3 4 5 6 7 Ref. -

Social Assessment Report (SA)
SFG2263 REV World Bank Loan Project Public Disclosure Authorized Shaanxi Poor Rural Areas Community Development Project (P153541) Public Disclosure Authorized Social Assessment Report (SA) Public Disclosure Authorized Undertaken by Shaanxi Provincial Foreign-funded Poverty Alleviation Project Management Center Compiled by Shaanxi Provincial Academy of Social Sciences May 2016 Public Disclosure Authorized Main Participants Person in charge of the Report: Wang Jiankang, Researcher and President of Shaanxi Provincial Academy of Social Sciences Authors: Luo Cheng, Researcher at Shaanxi Provincial Academy of Social Sciences Zhang Chunhua, Associate Researcher at Shaanxi Provincial Academy of Social Sciences Lai Zuolian, Associate Researcher at Shaanxi Provincial Academy of Social Sciences Li Bing, Associate Researcher at Shaanxi Provincial Academy of Social Sciences Yang Lan, Assistant Researcher at Shaanxi Provincial Academy of Social Sciences Feng Yuwen, Assistant Researcher at Shaanxi Provincial Academy of Social Sciences Wang Xiaojuan, Assistant Researcher at Shaanxi Provincial Academy of Social Sciences Ding Jieqing, Graduate student at Chang’an University Bao Yudan, Graduate student at Chang’an University Lu Shaobo, Graduate student at Chang’an University Data Analysts: Cheng Yuxi, Graduate student at Northwest University Zhang Maotuan, Graduate student at Xi’an Wenli College Min Dong Graduate student at Xi’an Wenli College Technology Consultant: Fang Haiyun, Associate Researcher at Shaanxi Provincial Academy of Social Sciences Expert -

Performance Evaluation and Comparison of Bivariate Statistical-Based Artificial Intelligence Algorithms for Spatial Prediction of Landslides
International Journal of Geo-Information Article Performance Evaluation and Comparison of Bivariate Statistical-Based Artificial Intelligence Algorithms for Spatial Prediction of Landslides Wei Chen 1,2,3,*, Zenghui Sun 1,2, Xia Zhao 3, Xinxiang Lei 3 , Ataollah Shirzadi 4 and Himan Shahabi 5,6 1 Key Laboratory of Degraded and Unused Land Consolidation Engineering, the Ministry of Natural Resources, Xi’an 710075, China; [email protected] 2 Shaanxi Provincial Land Engineering Construction Group Co. Ltd., Xi’an 710075, China 3 College of Geology & Environment, Xi’an University of Science and Technology, Xi’an 710054, China; [email protected] (X.Z.); [email protected] (X.L.) 4 Department of Rangeland and Watershed Management, Faculty of Natural Resources, University of Kurdistan, Sanandaj 66177-15175, Iran; [email protected] 5 Department of Geomorphology, Faculty of Natural Resources, University of Kurdistan, Sanandaj 66177-15175, Iran; [email protected] 6 Board Member of Department of Zrebar Lake Environmental Research, Kurdistan Studies Institute, University of Kurdistan, Sanandaj 66177-15175, Iran * Correspondence: [email protected] Received: 4 August 2020; Accepted: 22 November 2020; Published: 24 November 2020 Abstract: The purpose of this study is to compare nine models, composed of certainty factors (CFs), weights of evidence (WoE), evidential belief function (EBF) and two machine learning models, namely random forest (RF) and support vector machine (SVM). In the first step, fifteen landslide conditioning factors were selected to prepare thematic maps, including slope aspect, slope angle, elevation, stream power index (SPI), sediment transport index (STI), topographic wetness index (TWI), plan curvature, profile curvature, land use, normalized difference vegetation index (NDVI), soil, lithology, rainfall, distance to rivers and distance to roads.