Age of Computers Historiebok
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

NORSK DATA AS SINTRAN Iii Reference Manual
SINTRAN Il Reference Manual NORSK DATA AS SINTRAN IiI Reference Manual ND-60.128.03 NOTICE The information in this document is subject to change without notice. Norsk Data A.S assumes no responsibility for any errors that may appear in this document. Norsk Data A.S assumes no responsibility for-the use or reliability of its software on equipment that is not furnished or supported by Norsk Data A.S. The information described in this document is protected by copyright. It may not be photocopied, reproduced or translated without the prior consent of Norsk Data A.S. Copyright © 1983 by Norsk Data A.S This manual is in loose leaf form for ease of updating. Old pages may be removed and new pages easily inserted if the manual is revised. The loose leaf form also allows you to place the manual in a ring binder (A) for greater protection and convenience of use. Ring binders with 4 rings corre- sponding to the holes in the manual may be ordered in two widths, 30 mm and 40 mm. Use the order form below. The manual may also be placed in a plastic cover (B). This cover is more suitable for manuals of less than 100 pages than for large manuals. Plastic covers may also be ordered below. M= | ~ . IB== B 'S NORSK DATA AS NORSK DATA AS Bil=i & e lll\ ® A Ring Binder B Plastic Cover Please send your order to the local ND office or {in Norway) to: Documentation Department Norsk Data A.S P.0O. Box 4, Lindeberg gérd Oslo 10 ORDER FORM | would like to order Ring Binders, 30 mm, at nkr 20,- per binder Ring Binders, 40 mm, at nkr 25,- per binder Plastic Covers at nkr 10,- per cover NAME .. -

The Founding, Fantastic Growth, and Fast Decline of Norsk Data AS Tor Steine
The Founding, Fantastic Growth, and Fast Decline of Norsk Data AS Tor Steine To cite this version: Tor Steine. The Founding, Fantastic Growth, and Fast Decline of Norsk Data AS. 3rd History of Nordic Computing (HiNC), Oct 2010, Stockholm, Sweden. pp.249-257, 10.1007/978-3-642-23315- 9_28. hal-01564615 HAL Id: hal-01564615 https://hal.inria.fr/hal-01564615 Submitted on 19 Jul 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution| 4.0 International License The Founding, Fantastic Growth, and Fast Decline of Norsk Data AS Tor Olav Steine Formerly of Norsk Data AS [email protected] Abstract. Norsk Data was a remarkable company that in just twenty years went from a glimmer in the eyes of some computer enthusiasts to become number two in share value at the Oslo Stock Exchange. Within a few years thereafter, it collapsed, for no obvious reason. How was this tremendous success possible and why did the company collapse? Keywords: Collapse, computer, F16, industry, minicomputer, Norsk Data, Nord, simulator, success, Supermini 1 The Beginning 1.1 FFI A combination of circumstances led to the founding of Norsk Data1 in June 1967. -

Institutt for Teknisk Kybernetikk Femti År
Institutt for teknisk kybernetikk femti år Trondheim 2004 Utgitt av Institutt for teknisk kybernetikk til jubileumsfesten 10. 9. 2004 Redaksjon: Arne Asphjell Anne Kristine Børresen Forsiden: Den gamle og den nye tid: Instituttets grunnlegger Jens G. Balchen har vært en viktig drivkraft for instituttet i et halvt århundre. Kristin Ytterstad Pettersen repre- senterer den nye tid i den tidligere mannsbastionen. Foto: Rune Petter Ness. Heimdal Trykkeri Innhold Forord .................................................................................................................................................................. 3 1949-1960 Pionertid ............................................................................................................................................ 5 Fredstid, nybyggingstid ................................................................................................................................ 5 Jens G. Balchens barndom, ungdom og studietid......................................................................................... 8 Reguleringsmiljøet etableres ...................................................................................................................... 11 Diana .................................................................................................................................................... 11 Stadig på flyttefot ................................................................................................................................. 12 Reguleringsteknikk -

ND-60.151.02A SINTRAN III Utilities Manual February 1985
| ® | EO0CDRBERV0R DS \ 00200V HDRINCH D L R e g o SINTRAN [ Utilities Manual ND-60.151.02 Rev. A NOTICE The information in this document is subject to change without notice. Norsk Data A.S assumes no responsibility for any errors that may appear in this document. Norsk Data A.S assumes no responsibility for the use or reliability of its software on equipment that is not furnished or supported by Norsk Data A.S. The information described in this document is protected by copyright. It may not be photocopied, reproduced or translated without the prior consent of Norsk Data A.S. Copyright @ 1984 by Norsk Data A.S - PRINTING RECORD Printing Notes 11/81 Version 01 05/82 Revision A The following pages are revised or new: vi, vii, viii, 1—1, 3—=21. Sections 6 and 7. 12/82 Revision B The following pages are revised: vii. Section 5. 06/84 Version 02 02/85 Revision A The following sections are new: Sections 3 and 4. SINTRAN Il Utilities Manual Publ.No. ND--60.151.02A - =2 Norsk Data A.S . M Graphic Center P.0.Box 25, Bogerud t:l"orsk" Data 0621 Oslo 6, Norway iv Manuals can be updated in two ways, new versions and revisions. New versions consist of a8 complete new manual which replaces the old manual. New versions incorporate all revisions since the previous version. Revisions consist of one or more single pages to be merged into the manual by the user, each revised page being listed on the new printing record sent out with the revision. -

Norsk Data AS, the Fenomenon (Brief) Content
Norsk Data AS, The Fenomenon (brief) Tor Olav Steine, with the help of former colleaguesi . Abstract. Norsk Data was a remarkable company that went in just 20 years from a glimmer in the eyes of some computer enthusiasts to become number 2 in stock value at Oslo Stock Exchange. Then within a few years it collapsed, without obvious reason. How was this tremendous success possible and why did it collapse? NOTE: This history brief of the Norsk Data Company is based upon a Springer Verlag publication resulting from the HINC3 Conference in Stockholm 2010. It is ONLY for personal use, and not allowed for distribution or publishing. Content 1 The beginning ................................................................................................................................................. 2 2. The demanding customers .............................................................................................................................. 4 3 The years of fast growth ................................................................................................................................. 7 4. Crisis and downfall ......................................................................................................................................... 9 6. About the Author .......................................................................................................................................... 11 7. References ................................................................................................................................................... -

1 Interview of Rolf Skår Done by Email Over Many Days in September
Interview of Rolf Skår Done by email over many days in September 2012 A much shortened version of this interview was published in the IEEE Annals of the History of Computing, January-March 2013, pp. 72-77. The full interview, as approved by the interviewee, is being made available for the use of future historians. David Walden: Please tell me a bit about your youth [location, family, school before college, hobbies, sports, etc.] Rolf Skår: I was born at Skår, Karmøy in the Western coastal part of Norway. My father was a fisherman in the winter and a small farmer for the rest of the year. He spent 14 years as a construction worker in Canada before getting married to my mother. When I reached the age of 12, he bought his first car and a year later a tractor. He gave up the small farm when I left for NTH, and he returned to the work he did in Canada, mainly working with rock excavation. I come from a very large family with 71 first cousins, most of the male cousins either became fisherman or ship captains. My youth was dominated by “child labor”, working with my father on the small farm, and driving the tractor and doing work for the nearby neighbors. I started making my own money at the age of 14,doing work for other farmers nearby, and I have been financially independent of my parents since then, earning my spending money while at home and paying all expenses for attending university. There was little time for sports and hobbies. -
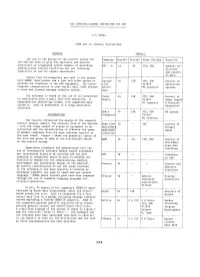
THE COMPUTER CONTROL SYSTEM for the SPS J.T. Hyman
THE COMPUTER CONTROL SYSTEM FOR THE SPS J.T. Hyman CERN Lab II, Geneva, Switzerland Summary Table 1 The aim in the design of the control system for Computer Core(k) Drum(k) Other Periphs. Function the SPS has been to give the operators and machine physicists an integrated system capable of providing GP1 - 6 16 64 TTY, VDU sophisticated control facilities but yet retaining General Ac-qisition simplicity of use for normal operations. and control in BA's Twenty four minicomputers are used in the system with CAMAC input/output and a fast multiplex system to Extrac 24 128 TTY, VDU Control of provide the interface to the SPS equipment. The inter tion PT-R/P Extraction computer communication is over serial data links through North/ MT cassette systems a store and forward message transfer system. West The software is based on the use of an interpreter Power 24 128 TTY, VDU Control of in conjunction with a small real-time executive. A Supply PT-R/P Power Supply comprehensive addressing scheme, with segmented data MT cassette & Function tables is used in preference to a large monolithic Generators structure. Radio 24 128 TTY, VDU RF system Introduction Frequency PT-R/P MT cassette Two factors influenced the design of the computer control system, namely, the physical size of the machine Beam Line 16 - TTY Control of - with the large number of pieces of equipment to be North/West Primary controlled and the determination to liberate the power BA80/WRB2 Beams of modern computers from the past software barrier at Injection the user level. -

The Language List - Version 2.4, January 23, 1995
The Language List - Version 2.4, January 23, 1995 Collected information on about 2350 computer languages, past and present. Available online as: http://cui_www.unige.ch/langlist ftp://wuarchive.wustl.edu/doc/misc/lang-list.txt Maintained by: Bill Kinnersley Computer Science Department University of Kansas Lawrence, KS 66045 [email protected] Started Mar 7, 1991 by Tom Rombouts <[email protected]> This document is intended to become one of the longest lists of computer programming languages ever assembled (or compiled). Its purpose is not to be a definitive scholarly work, but rather to collect and provide the best information that we can in a timely fashion. Its accuracy and completeness depends on the readers of Usenet, so if you know about something that should be added, please help us out. Hundreds of netters have already contributed to this effort. We hope that this list will continue to evolve as a useful resource available to everyone on the net with an interest in programming languages. "YOU LEFT OUT LANGUAGE ___!" If you have information about a language that is not on this list, please e-mail the relevant details to the current maintainer, as shown above. If you can cite a published reference to the language, that will help in determining authenticity. What Languages Should Be Included The "Published" Rule - A language should be "published" to be included in this list. There is no precise criterion here, but for example a language devised solely for the compiler course you're taking doesn't count. Even a language that is the topic of a PhD thesis might not necessarily be included. -

ND-60.134.02 SINTRAN III Communication Guide November
SINTRAN 111 Communication Guide ND-60.134.02 NOTICE The information in this document is subject to change without notice. Norsk Data A.S assumes no responsibility for any errors that may appear in this document. Norsk Data A.S assumes no responsibility for the use or reliability of its software on equipment that is not furnished or supported by Norsk Data A.S. The information described in this document is protected by copyright. It may not be photocopied, reproduced or translated without the prior consent of Norsk Data A.S. Copyright © 1981 by Norsk Data A.S. This manual is in loose leaf form for ease of updauing. Old pages may be removed and new pages easily inserted if the manual is revised. The loose teaf form aiso allows you to place the manual in a ring binder (A) for greater protection and convenience of use. Ring binders with 4 rings corre- sponding to the holes in the manual may be ordered in two widths, 30 mm and 40 mm. Use the order form below. The manual may also be placed in a plastic cover {B). This cover is more suitable for manuals of less than 100 pages than for large manuals. Plastic covers may also be ordered below. \ P =D | . 7 N NCRSK DATA AS NQRSK DATA AS ~ B 322, IS B I, B = 8 B 8 ag g 8 Tk anes n‘ g A Ring Binder B Plastic Cover Please send your order to the local ND office or (in Norway) to: Documentation Department Norsk Data A.S P.0. -

System Software of the Cern Proton Synchrotron Control System
CERN 84-16 Proton Synchrotron Division 20 December 1984 ORGANISATION EUROPÉENNE POUR LA RECHERCHE NUCLÉAIRE CERN EUROPEAN ORGANIZATION FOR NUCLEAR RESEARCH SYSTEM SOFTWARE OF THE CERN PROTON SYNCHROTRON CONTROL SYSTEM B.E. Carpenter, R. Cailliau, G. Cuisinier and W. Remmer GENEVA 1984 © Copyright CERN, Genève, 1984 Propriété littéraire et scientifique réservée pour Literary and scientific copyrights reserved in all tous les pays du monde. Ce document ne peut countries of the world. This report, or any part of être reproduit ou traduit en tout ou en partie sans it, may not be reprinted or translated without l'autorisation écrite du Directeur général du written permission of the copyright holder, the CERN, titulaire du droit d'auteur. Dans les cas Director-General of CERN. However, permission appropriés, et s'il s'agit d'utiliser le document à will be freely granted for appropriate non des fins non commerciales, cette autorisation commercial use. sera volontiers accordée. If any patentable invention or registrable design Le CERN ne revendique pas la propriété des is described in the report, CERN makes no claim inventions brevetables et dessins ou modèles to property rights in it but offers it for the free use susceptibles de dépôt qui pourraient être décrits of research institutions, manufacturers and dans le présent document; ceux-ci peuvent être others. CERN, however, may oppose any attempt librement utilisés par les instituts de recherche, by a user to claim any proprietary or patent rights les industriels et autres intéressés. Cependant, le in such inventions or designs as may be des CERN se réserve le droit de s'opposer à toute cribed in the present document. -

My Corner of the Time-Sharing Innovation World
qM qMqM Previous Page | Contents |Zoom in | Zoom out | Front Cover | Search Issue | Next Page qMqM Qmags THE WORLD’S NEWSSTAND® My Corner of the Time-Sharing Innovation World Bo Lewendal Editor: David Walden As with many people, the path of my career in comput- was to be used for, but I later learned that it was a pro- ing had unexpected changes of direction, in my case totype to be used for part of the development of a relating to the time I entered computing and my completely new time-sharing system (more about this national background. I was fortunate to have a small later). role in spreading the then new technology of computer Although I was hired as an electronics technician, time-sharing systems. the leaders of the project also let me play with the time- My parents were from Sweden and I was born there. sharing system, which I used from a Teletype terminal. In 1949, when I was one year old, our family moved to Over time, I drifted into programming and my title was California, where my father studied for three years for a changed to “coder.” In that role, one of the projects I master’s degree at the University of California, Berkeley. worked on was coding for a PhD student working on Then we returned to Sweden, living in Stockholm for recognizing letters printed by hand on a Rand tablet three years. connected to a PDP-5 with an Evans & Sutherland vec- However, my parents had loved California, and tor display. The resulting software also provided the when I was seven years old, we moved to New York equivalent of a mouse in addition to text entry. -

The Founding, Fantastic Growth, and Fast Decline of Norsk Data AS
The Founding, Fantastic Growth, and Fast Decline of Norsk Data AS Tor Olav Steine Formerly of Norsk Data AS [email protected] Abstract. Norsk Data was a remarkable company that in just twenty years went from a glimmer in the eyes of some computer enthusiasts to become number two in share value at the Oslo Stock Exchange. Within a few years thereafter, it collapsed, for no obvious reason. How was this tremendous success possible and why did the company collapse? Keywords: Collapse, computer, F16, industry, minicomputer, Norsk Data, Nord, simulator, success, Supermini. 1 The Beginning 1.1 FFI A combination of circumstances led to the founding of Norsk Data1 in June 1967. Several brilliant researchers came together at the Norwegian Defense Research Institute (FFI)2 in Kjeller outside Oslo, Norway. Under institute director Finn Lied, division director of telecommunications Karl Holberg initiated a digital group and appointed Yngvar Lundh as its project leader. Lars Monrad-Krohn was appointed leader of the digital lab. Yngvar Lundh had experience as a researcher at MIT (Cambridge, MA) during a stay in 1959, Monrad-Krohn followed with a similar appointment in 1962–64, while Per Bjørge, another brilliant computer developer, did his own MIT tour during 1966. These researchers were impressed with the fast development of computer technology at MIT [1, 2] and soon FFI was itself active in the field, building two military systems, SAM and SAM2. Due to the fact that SAM2 was being built with the new Dual-In-Line (DIP) Integrated Circuit technology, it also had civil potential. In time, the idea of launching a spin-off company for the civilian market was born.