DOCSLIB.ORG

Low Flow of Streams in the Susquehanna River Basin of New York

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Low Flow of Streams in the Susquehanna River Basin of New York Low Flow of Streams in the Susquehanna River Basin of New York Scientific Investigations Report 2010–5063 U.S. Department of the Interior U.S. Geological Survey Cover. Cuthrie Run, 3 miles north of Big Flats, Chemung County, New York, within an upland valley that drains 5.3 square miles. Photograph by Matthew B. Jennings, U.S. Geological Survey, June 29, 2007, when streamflow in this region was moderately low (exceeded about 80 percent of the time). Low Flow of Streams in the Susquehanna River Basin of New York By Allan D. Randall Scientific Investigations Report 2010–5063 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior KEN SALAZAR, Secretary U.S. Geological Survey Marcia K. McNutt, Director U.S. Geological Survey, Reston, Virginia: 2010 For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment, visit http://www.usgs.gov or call 1-888-ASK-USGS For an overview of USGS information products, including maps, imagery, and publications, visit http://www.usgs.gov/pubprod To order this and other USGS information products, visit http://store.usgs.gov Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. Suggested citation: Randall, A.D., 2010, Low flow of streams in the Susquehanna River basin of New York: U.S. Geological Survey Scientific Investigations Report 2010–5063, 57 p., at http://pubs.usgs.gov/sir/2010/5063. iii Contents Abstract ...........................................................................................................................................................1 Introduction.....................................................................................................................................................1 Watershed Properties and Processes that Control Spatial Variation in Low Flow of Streams ........3 Amount of Water Available for Runoff .............................................................................................3 Annual Precipitation and Runoff ...............................................................................................3 Seasonal Precipitation and Runoff ...........................................................................................5 Extent and Properties of Surficial Sand and Gravel .......................................................................8 Modeling Properties of Surficial Sand and Gravel that Affect Groundwater Discharge to Streams .................................................................................................10 Analytical Model ..............................................................................................................10 Numerical Model ..............................................................................................................11 Model Configuration and Operation .....................................................................14 Model Evaluation .....................................................................................................15 Evapotranspiration from Wetlands ..................................................................................................18 Underflow beneath Sites of Streamflow Measurement ..............................................................19 Less Important Factors that Affect Low Flows ..............................................................................22 Watershed Area .........................................................................................................................22 Extent and Properties of Till .....................................................................................................22 Extent and Properties of Bedrock Units .................................................................................22 Watershed Relief and Slope ....................................................................................................23 Degree of Stream Regulation and Watershed Urbanization ..............................................24 Regression Analysis ....................................................................................................................................24 Data Set ...............................................................................................................................................24 Low-Flow Statistics ...................................................................................................................24 Watershed Properties ...............................................................................................................28 Format of Regression Equations .....................................................................................................32 Standard-Value Equations to Estimate 7-Day, 10-Year Low Flows ...................................33 Effect of Sand-and-Gravel Area and Wetland Area ...................................................33 Effect of Amount of Water Available .............................................................................33 Other Variables and Data Manipulations Tested .........................................................35 Per-Square-Mile Equations to Estimate 7-Day, 10-Year Low Flows ..................................38 Comparison of Per-Square-Mile Equations with Standard-Value Equations .........38 Evaluation of the Data Set and Equations ....................................................................38 Effect of Underflow ..........................................................................................................42 Logarithmic Equations to Estimate 7-Day, 10-Year Low Flows ..........................................42 A Critique of the Rationale for Logarithmic Transformation ......................................42 Comparison of Logarithmic Equations with Standard-Value Equations ..................43 Equations to Estimate 7-Day, 2-Year Low Flow and 90-Percent Flow Duration ..............44 Suggested Methods for Estimating Low-Flow Characteristics at Ungaged Sites ............................46 Watersheds Larger Than 30 Square Miles .....................................................................................47 Watersheds Smaller Than 30 Square Miles ...................................................................................47 Summary........................................................................................................................................................48 Acknowledgments .......................................................................................................................................49 References Cited .........................................................................................................................................49 iv Figures 1. Map showing location of the Susquehanna River basin and physiographic regions in New York and adjacent States ...............................................................................................2 2. Diagram showing principal environmental factors that control the low flow of streams in the glaciated northeastern United States .............................................................4 3. Maps showing spatial variation in A, mean annual precipitation and B, mean annual runoff in the Susquehanna River basin of New York, 1951–80 .................................6 4. Map showing ratios of mean August–October runoff to mean annual runoff for the period April 1937 to March 1963 in the Susquehanna River basin and adjacent areas ...9 5. Diagram showing idealized aquifer represented by analytical equations of Rorabaugh (1963) ........................................................................................................................11 6. Graphs showing effect of A, valley width and B, aquifer transmissivity on groundwater discharge to a stream during a period of low flow, as calculated from equations of Rorabaugh (1963) .................................................................................................12 7. Diagram showing dimensions and properties of a two-dimensional groundwater-flow model that represents an idealized vertical section across an upland hillside and the adjacent valley ...................................................................................13 8. Graph showing simulated groundwater discharge, to a stream and as evapotranspiration, from an idealized upland hillside and valley fill after 4 months without recharge, as a function of hydraulic conductivity of the valley fill ......................16 9. Graph showing simulated groundwater discharge to a stream from an idealized valley fill after 4 months without recharge, as a function of valley half-width ................18 10. Map showing locations of streamflow-measurement stations in the Susquehanna River basin of New York .............................................................................................................20 11. Graph showing correlation of 7Q10 calculated from streamflow measurements with 7Q10 estimated using equation 3 .....................................................................................34 12. Graph showing distribution of residuals from equation 5 ....................................................36
Load more

Recommended publications
  • NON-TIDAL BENTHIC MONITORING DATABASE: Version 3.5
    NON-TIDAL BENTHIC MONITORING DATABASE: Version 3.5 DATABASE DESIGN DOCUMENTATION AND DATA DICTIONARY 1 June 2013 Prepared for: United States Environmental Protection Agency Chesapeake Bay Program 410 Severn Avenue Annapolis, Maryland 21403 Prepared By: Interstate Commission on the Potomac River Basin 51 Monroe Street, PE-08 Rockville, Maryland 20850 Prepared for United States Environmental Protection Agency Chesapeake Bay Program 410 Severn Avenue Annapolis, MD 21403 By Jacqueline Johnson Interstate Commission on the Potomac River Basin To receive additional copies of the report please call or write: The Interstate Commission on the Potomac River Basin 51 Monroe Street, PE-08 Rockville, Maryland 20850 301-984-1908 Funds to support the document The Non-Tidal Benthic Monitoring Database: Version 3.0; Database Design Documentation And Data Dictionary was supported by the US Environmental Protection Agency Grant CB- CBxxxxxxxxxx-x Disclaimer The opinion expressed are those of the authors and should not be construed as representing the U.S. Government, the US Environmental Protection Agency, the several states or the signatories or Commissioners to the Interstate Commission on the Potomac River Basin: Maryland, Pennsylvania, Virginia, West Virginia or the District of Columbia. ii The Non-Tidal Benthic Monitoring Database: Version 3.5 TABLE OF CONTENTS BACKGROUND ................................................................................................................................................. 3 INTRODUCTION ..............................................................................................................................................
    [Show full text]
  • Town of Otsego Comprehensive Plan Appendices
    Town of Otsego Comprehensive Plan Appendices Draft (V6) March 2007 Town of Otsego Comprehensive Plan – Draft March 2007 Table of Contents Appendix A Consultants Recommendations to Implement Plan A1 Appendix B 2006 Update: Public Input B1 Appendix C 2006 Update: Profile and Inventory of Town Resources C1 Appendix D Zoning Build-out Analysis D1 Appendix E Strengths, Weaknesses, Opportunities and Threats Analysis E1 Appendix F 1987 Master Plan F1 Appendix G Ancillary Maps G1 See separate document for Comprehensive Plan: Section 1 Introduction Section 2 Summary of Current Conditions and Issues Section 3 Vision Statement Section 4 Goals Section 5 Strategies to Implement Goals Section 6 Mapped Resources Appendix A Consultants Recommendations to Implement Plan APPENDIX A-1 Town of Otsego Comprehensive Plan – Draft March 2007 Appendix A. Consultants Recommendations to Implement Plan This section includes strategies, actions, policy changes, programs and planning recommendations presented by the consultants (included in the plan as reference materials) that could be undertaken by the Town of Otsego to meet the goals as established in this Plan. They are organized by type of action. Recommended Strategies Regulatory and Project Review Initiatives 1. Utilize the Final GEIS on the Capacities of the Cooperstown Region in decision making in the Town of Otsego. This document analyzes and identifies potential environmental impacts to geology, aquifers, wellhead protection areas, surface water, Otsego Lake and Watershed, ambient light conditions, historic resources, visual resources, wildlife, agriculture, on-site wastewater treatment, transportation, emergency services, demographics, economic conditions, affordable housing, and tourism. This document will offer the Planning Board and other Town agencies, background information, analysis, and mitigation to be used to minimize environmental impacts of future development.
    [Show full text]
  • A Characterization of the Riparian Corridor of the Oaks Creek Blueway Trail with Emphasis on Otsego Land Trust Properties
    A characterization of the riparian corridor of the Oaks Creek Blueway Trail with emphasis on Otsego Land Trust properties Nicole Pedisich1 and Donna Vogler2 INTRODUCTION The Otsego Land Trust Blueway is a series of Land Trust owned and protected parcels that provide fishing, hiking, paddling, bird watching, and educational opportunities from Canadarago Lake to the Susquehanna River including Brookwood Point on Otsego Lake. (Otsego Land Trust 2014). The trail consists of Fetterly Forest, Deowongo Island, Oaks Creek Preserve, Crave, Parslow Road, Greenough Road, and Compton Bridge. For this project, an assessment of the riparian vegetation communities of Oaks Creek was conducted along a section of the Blueway Trail starting in Schuyler Lake and ending in Cattown. More in-depth characterizations of plant communities were done at Oaks Creek Preserve, the Crave property, and Parslow Road Conservation Area. Oaks Creek is a stream located in Otsego County, NY. It flows from Canadarago Lake southeast into the Susquehanna River, a distance of approximately 13.8 miles. (Hingula 2004). A majority of the stretch of stream assessed is state-regulated freshwater wetlands (Figure 1, NYSDEC). Oaks Creek Preserve is a 28-acre parcel located along its namesake between Schuyler Lake and Oaksville. Downstream are Crave, a parcel recently acquired by the Otsego Land Trust and Parslow Road Conservation Area, an 86-acre parcel located on the northern edge of Oaksville running a half-mile along Oaks Creek (Figure 2). 3 1 BFS Intern, summer 2015. Current affiliation: SUNY College at Oneonta. Funding for this project was provided by the Otsego Land Trust. 2 Professor.
    [Show full text]
  • Susquehanna Riyer Drainage Basin
    'M, General Hydrographic Water-Supply and Irrigation Paper No. 109 Series -j Investigations, 13 .N, Water Power, 9 DEPARTMENT OF THE INTERIOR UNITED STATES GEOLOGICAL SURVEY CHARLES D. WALCOTT, DIRECTOR HYDROGRAPHY OF THE SUSQUEHANNA RIYER DRAINAGE BASIN BY JOHN C. HOYT AND ROBERT H. ANDERSON WASHINGTON GOVERNMENT PRINTING OFFICE 1 9 0 5 CONTENTS. Page. Letter of transmittaL_.__.______.____.__..__.___._______.._.__..__..__... 7 Introduction......---..-.-..-.--.-.-----............_-........--._.----.- 9 Acknowledgments -..___.______.._.___.________________.____.___--_----.. 9 Description of drainage area......--..--..--.....-_....-....-....-....--.- 10 General features- -----_.____._.__..__._.___._..__-____.__-__---------- 10 Susquehanna River below West Branch ___...______-_--__.------_.--. 19 Susquehanna River above West Branch .............................. 21 West Branch ....................................................... 23 Navigation .--..........._-..........-....................-...---..-....- 24 Measurements of flow..................-.....-..-.---......-.-..---...... 25 Susquehanna River at Binghamton, N. Y_-..---...-.-...----.....-..- 25 Ghenango River at Binghamton, N. Y................................ 34 Susquehanna River at Wilkesbarre, Pa......_............-...----_--. 43 Susquehanna River at Danville, Pa..........._..................._... 56 West Branch at Williamsport, Pa .._.................--...--....- _ - - 67 West Branch at Allenwood, Pa.....-........-...-.._.---.---.-..-.-.. 84 Juniata River at Newport, Pa...-----......--....-...-....--..-..---.-
    [Show full text]
  • Otsego County Water Quality Coordinating Committee Annual Report 2010 & 2011
    Otsego County Water Quality Coordinating Committee Annual Report 2010 & 2011 Prepared by: Otsego County Water Quality Coordinating Committee 967 County Highway 33 Cooperstown, NY 13326 6/18/2012 Table of Contents INTRODUCTION OF WATER QUALITY COORDINATING COMMITTEE 2 COORDINATING COMMITTEE MEMBERS 2 COMMITTEE MISSION, PURPOSE AND PRIMARY FUNCTIONS 3 2010 ACCOMPLISHMENTS 5 2011 ACCOMPLISHMENTS 7 ATTACHMENTS: #1 Water Quality Coordinating Committee By Laws #2 2011 Otsego County Nonpoint Source Water Quality Strategy #3 Susquehanna Headwaters Nutrient Report #4 Otsego County Soil & Water Conservation District 2011 Report #5 Otsego County Conservation Association 2011 Report #6 Goodyear Lake Association 2011 Report #7 Otsego Lake Watershed Supervisory Committee 2011 Report #8 SUNY Oneonta Biological Field Station 2011 Staff Activity Report #9 Village of Richfield 2011 Water Quality Report 1 INTRODUCTION OTSEGO COUNTY WATER QUALITY COORDINATING COMMITTEE Non-point pollution (NPS) by definition is any form of pollution not being discharged from a distinguished point or source. Sources of NPS, being so diffuse and variable, will often require multi-agency involvement to remediate the existing water pollution problems. Understanding that the responsibility and interest in water quality issues are represented by a wide range of parties, a committee was formed and is known as the Otsego County Water Quality Coordinating Committee (the Committee) and functions as a subcommittee of the Otsego County Soil and Water Conservation District. The Committee is responsible for the preparation of the Otsego County Non-point Source Water Quality Strategy. The Strategy attempts to ensure that the individual efforts of local, county, state, and federal agencies regarding water quality programs and educational outreach events are coordinated for maximum effectiveness.
    [Show full text]
  • Public Fishing Rights Maps: Otego Creek
    Public Fishing Rights Maps Otego Creek Fish Species Present About Public Fishing Rights Brown Trout Public Fishing Rights (PFR’s) are permanent easements purchased by the NYSDEC from will- ing landowners, giving anglers the right to fish and walk along the bank (usually a 33’ strip on Brook Trout one or both banks of the stream). This right is for the purpose of fishing only and no other purpose. Treat the land with respect to insure the continua- tion of this right and privilege. Fishing privileges may be available on some other private lands with Description of Fishery permission of the land owner. Courtesy toward the land-owner and respect for their property will Otego Creek flows for 29 miles before entering the insure their continued use. Susquehanna River west of Oneonta. The lower 10 miles supports a low quality warmwater fish- These generalized location maps are intended to ery for walleye, smallmouth bass, and rock bass. aid anglers in finding PFR segments and are not From Laurens upstream to Hartwick, the wild trout survey quality. Width of displayed PFR may be population in this 14.6 mile reach is supplemented wider than reality to make it more visible on the with the stocking of approximately 2,900 yearling maps. Please look for this PFR sign to ensure that and 125 two year old brown trout annually. Brown you are in the right location and have legal access trout abundance is higher in the lower reach and to the stream bank. brook trout in the upper reach. Many of the tribu- taries to Otego Creek are dominated by wild brook trout.
    [Show full text]
  • Upper Susquehanna Subbasin Survey: a Water Quality and Biological Assessment, June – September 2007
    Upper Susquehanna Subbasin Survey: A Water Quality and Biological Assessment, June – September 2007 The Susquehanna River Basin Commission (SRBC) conducted a water quality and biological survey of the Upper Susquehanna Subbasin from June to September 2007. This survey is part of SRBC’s Subbasin Survey Program, which is funded in part by the United States Environmental Protection Agency (USEPA). The Subbasin Survey Program consists of two- year assessments in each of the six major subbasins (Figure 1) on a rotating schedule. This report details the Year-1 survey, which consists of point-in-time water chemistry, macroinvertebrate, and habitat data collection and assessments of the major tributaries and areas of interest throughout the Upper Susquehanna Subbasin. The Year-2 survey will be conducted in the Tioughnioga River over a one-year time period beginning in summer 2008. The Year-2 survey is part of a larger monitoring effort associated with an environmental restoration effort at Whitney Point Lake. Previous SRBC surveys of the Upper Susquehanna Subbasin were conducted in 1998 (Stoe, 1999) and 1984 (McMorran, 1985). Subbasin survey information is used by SRBC staff and others to: • evaluate the chemical, biological, and habitat conditions of streams in the basin; • identify major sources of pollution and lengths of streams impacted; • identify high quality sections of streams that need to be protected; • maintain a database that can be used to document changes in stream quality over time; • review projects affecting water quality in the basin; and • identify areas for more intensive study. Description of the Upper Susquehanna Subbasin The Upper Susquehanna Subbasin is an interstate subbasin that drains approximately 4,950 square miles of southcentral New York and a small portion of northeastern Pennsylvania.
    [Show full text]
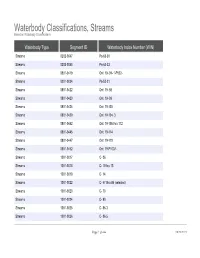
  • Waterbody Classifications, Streams Based on Waterbody Classifications
    Waterbody Classifications, Streams Based on Waterbody Classifications Waterbody Type Segment ID Waterbody Index Number (WIN) Streams 0202-0047 Pa-63-30 Streams 0202-0048 Pa-63-33 Streams 0801-0419 Ont 19- 94- 1-P922- Streams 0201-0034 Pa-53-21 Streams 0801-0422 Ont 19- 98 Streams 0801-0423 Ont 19- 99 Streams 0801-0424 Ont 19-103 Streams 0801-0429 Ont 19-104- 3 Streams 0801-0442 Ont 19-105 thru 112 Streams 0801-0445 Ont 19-114 Streams 0801-0447 Ont 19-119 Streams 0801-0452 Ont 19-P1007- Streams 1001-0017 C- 86 Streams 1001-0018 C- 5 thru 13 Streams 1001-0019 C- 14 Streams 1001-0022 C- 57 thru 95 (selected) Streams 1001-0023 C- 73 Streams 1001-0024 C- 80 Streams 1001-0025 C- 86-3 Streams 1001-0026 C- 86-5 Page 1 of 464 09/28/2021 Waterbody Classifications, Streams Based on Waterbody Classifications Name Description Clear Creek and tribs entire stream and tribs Mud Creek and tribs entire stream and tribs Tribs to Long Lake total length of all tribs to lake Little Valley Creek, Upper, and tribs stream and tribs, above Elkdale Kents Creek and tribs entire stream and tribs Crystal Creek, Upper, and tribs stream and tribs, above Forestport Alder Creek and tribs entire stream and tribs Bear Creek and tribs entire stream and tribs Minor Tribs to Kayuta Lake total length of select tribs to the lake Little Black Creek, Upper, and tribs stream and tribs, above Wheelertown Twin Lakes Stream and tribs entire stream and tribs Tribs to North Lake total length of all tribs to lake Mill Brook and minor tribs entire stream and selected tribs Riley Brook
    [Show full text]
  • Section 4: County Profile
    SECTION 4: COUNTY PROFILE SECTION 4: COUNTY PROFILE Broome County profile information is presented in the plan and analyzed to develop an understanding of a study area, including the economic, structural, and population assets at risk and the particular concerns that may be present related to hazards analyzed later in this plan (e.g., low lying areas prone to flooding or a high percentage of vulnerable persons in an area). This profile provides general information for Broome County (physical setting, population and demographics, general building stock, and land use and population trends) and critical facilities located within the County. GENERAL INFORMATION Broome County is a rural community located within the south-central part or “Southern Tier” of New York State. The Southern Tier is a geographical term that refers to the counties of New York State that lie west of the Catskill Mountains, along the northern border of Pennsylvania. Broome County lies directly west of Delaware County, 137 miles southwest of Albany and approximately 177 miles northwest of New York City. Broome County occupies approximately 715 square miles and has a population of approximately 199,031 (U.S. Census, 2011). Broome County is one of the 62 counties in New York State and is comprised of one city, sixteen towns, seven villages and many hamlets. The City of Binghamton is the County seat and is located at the confluence of the Susquehanna and Chenango Rivers. The City of Binghamton is part of the “Triple Cities,” which also includes the Villages of Endicott and Johnson City. With two Interstates and a major state route intersecting in the City of Binghamton, the area is the crossroads of the Southern Tier.
    [Show full text]
  • Brook Trout Outcome Management Strategy
    Brook Trout Outcome Management Strategy Introduction Brook Trout symbolize healthy waters because they rely on clean, cold stream habitat and are sensitive to rising stream temperatures, thereby serving as an aquatic version of a “canary in a coal mine”. Brook Trout are also highly prized by recreational anglers and have been designated as the state fish in many eastern states. They are an essential part of the headwater stream ecosystem, an important part of the upper watershed’s natural heritage and a valuable recreational resource. Land trusts in West Virginia, New York and Virginia have found that the possibility of restoring Brook Trout to local streams can act as a motivator for private landowners to take conservation actions, whether it is installing a fence that will exclude livestock from a waterway or putting their land under a conservation easement. The decline of Brook Trout serves as a warning about the health of local waterways and the lands draining to them. More than a century of declining Brook Trout populations has led to lost economic revenue and recreational fishing opportunities in the Bay’s headwaters. Chesapeake Bay Management Strategy: Brook Trout March 16, 2015 - DRAFT I. Goal, Outcome and Baseline This management strategy identifies approaches for achieving the following goal and outcome: Vital Habitats Goal: Restore, enhance and protect a network of land and water habitats to support fish and wildlife, and to afford other public benefits, including water quality, recreational uses and scenic value across the watershed. Brook Trout Outcome: Restore and sustain naturally reproducing Brook Trout populations in Chesapeake Bay headwater streams, with an eight percent increase in occupied habitat by 2025.
    [Show full text]
  • Selected Streamflow Statistics for Streamgage Locations in and Near Pennsylvania
    Prepared in cooperation with the Pennsylvania Department of Environmental Protection Selected Streamflow Statistics for Streamgage Locations in and near Pennsylvania Open-File Report 2011–1070 U.S. Department of the Interior U.S. Geological Survey Cover. Tunkhannock Creek and Highway 6 overpass downstream from U.S. Geological Survey streamgage 01534000 Tunkhannock Creek near Tunkhannock, PA. (Photo by Andrew Reif, USGS) Selected Streamflow Statistics for Streamgage Locations in and near Pennsylvania By Marla H. Stuckey and Mark A. Roland Prepared in cooperation with the Pennsylvania Department of Environmental Protection Open-File Report 2011–1070 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior KEN SALAZAR, Secretary U.S. Geological Survey Marcia K. McNutt, Director U.S. Geological Survey, Reston, Virginia: 2011 For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment, visit http://www.usgs.gov or call 1–888–ASK–USGS. For an overview of USGS information products, including maps, imagery, and publications, visit http://www.usgs.gov/pubprod To order this and other USGS information products, visit http://store.usgs.gov Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. Suggested citation: Stuckey, M.H., and Roland, M.A., 2011, Selected streamflow statistics for streamgage locations in and near Pennsyl- vania: U.S.
    [Show full text]
  • Index of Surface-Water Records
    ~EOLOGICAL SURVEY CIRCULAR 138 July 1951 INDEX OF SURFACE-WATER RECORDS PART I.-NORTH ATLANTIC SLOPE BASINS TO SEPTEMBER 30, 1950 Prepared by Boston District UNITED STATES DEPARTMENT OF THE INTERIOR Oscar L. Chapman, Secretary GEOLOGICAL SURVEY W. E. Wrather, Director Washington, 'J. C. Free on application to the Geological Survey, Washington 26, D. C. INDEX OF SURFACE-WATER RECORDS PART 1.-NORTH ATLANTIC SLOPE BASINS TO SEPTEMBER 30, 1950 EXPLANATION The index lists the stream-flow and reservoir stations in the North Atlantic Slope Basins for which records have been or are to be published for periods prior to Sept. 30, 1950. The stations are listed in downstream order. Tributary streams are indicated by indention. Station names are given in their most recently published forms. Parentheses around part of a station name indicate that the inclosed word or words were used in an earlier published name of the station or in a name under which records were published by some agency other than the Geological Survey. The drainage areas, in square miles, are the latest figures pu~lished or otherwise available at this time. Drainage areas that were obviously inconsistent with other drainage areas on the same stream have been omitted. Under "period of record" breaks of less than a 12-month period are not shown. A dash not followed immediately by a closing date shows that the station was in operation on September 30, 1950. The years given are calendar years. Periods·of records published by agencies other than the Geological Survey are listed in parentheses only when they contain more detailed information or are for periods not reported in publications of the Geological Survey.
    [Show full text]