Redefining the Decathlon Scoring Tables
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Athletics (Track & Field) 2015 General Rules
ATHLETICS (TRACK & FIELD) 2015 GENERAL RULES The Official Special Olympics Sports Rules shall govern all Special Olympics athletics competitions. As an international sports program, Special Olympics has created these rules based upon Internationale Amateur Athletic Federation (IAAF) and National Governing Body (NGB) rules for athletics. IAAF or National Governing Body rules shall be employed except when they are in conflict with the Official Special Olympics Sports Rules. For more information, visit www.iaaf.org. DEVELOPMENTAL EVENTS 1. Assisted Run (regional level only, non-advancing) 2. 50m Run* 3. 25m Walk* 4. Standing Long Jump* 5. Softball Throw* (Athletes throwing over 15m should compete in the shot put or mini jav; athletes who have thrown more than 20m in a SOWI competition will be ineligible to participate in softball throw following that season.) 6. 25m Non-Motorized Wheelchair* 7. 30m Non-Motorized Wheelchair Slalom* 8. 30 and 50m Motor Wheelchair Slalom* 9. 25m Motor Wheelchair Obstacle Course* 10. 4x25m Non-Motorized Wheelchair Shuttle Relay* *These events with an asterisk are considered developmental events and provide meaningful competition for athletes with lower ability levels and are not meant to be paired with other events (except field events) when entering athletes in competition. OFFICIAL EVENTS OFFERED 1. 100, 200, 400, 800, 1500, 3000m Run 8. 4x100m Relay 2. 100, 200, 400*, 800*, 1500m* Walk 9. 4x200 m Relay 3. High Jump – no longer offered as an event 10. 4x400m Relay 4. Long Jump 11. Pentathalon – no longer offered as an event 5. Shot Put 12. 100, 200m Non-Motorized Wheelchair 6. Mini Jav (formerly known as Turbo Jav) 13. -

Miami's Olympians
Year-by-Year Results MEN’S MAC RESULTS RECORDS BY SEASON** Year CC IT&F OT&F Coach Year CC IT&F OT&F Coach 1947-48 1st - 1st George Rider 1984-85 1st - 4th Chuck Zody 1948-49 2nd - 1st George Rider 1985-86 1st - 3rd Chuck Zody 1949-50 1st - 1st George Rider 1986-87 2nd - 3rd Chuck Zody 1950-51 1st - 1st George Rider 1987-88 5th - 4th Chuck Zody 1951-52 1st - 1st George Rider 1988-89 5th - 3rd Chuck Zody 1952-53 1st - 1st George Rider 1989-90 8th - 6th Chuck Zody 1953-54 1st - 1st George Rider 1990-91 3rd - 3rd Chuck Zody 1954-55 1st - 1st George Rider 1991-92 7th - 3rd Chuck Zody 1955-56 1st - 1st George Rider 1992-93 4th - 1st Chuck Zody 1956-57 1st - 1st George Rider 1993-94 2nd - 2nd Chuck Zody 1957-58 3rd - 3rd George Rider 1994-95 t-5th - 8th Warren Mandrell 1958-59 2nd - 4th George Rider 1995-96 6th 8th 5th Warren Mandrell 1959-60 2nd - 2nd George Rider 1996-97 2nd - 6th Warren Mandrell 1960-61 2nd - 2nd George Rider 1997-98 1st - 5th Warren Mandrell 1961-62 2nd - 2nd Bob Epskamp 1998-99 1st - 5th Warren Mandrell 1962-63 4th - 3rd Bob Epskamp 1999-00 2nd - 10th Warren Mandrell 1963-64 3rd - 2nd Bob Epskamp 2000-01 t-2nd - 7th Warren Mandrell 1964-65 3rd - 3rd Bob Epskamp 2001-02 2nd - 11th Warren Mandrell 1965-66 1st - 2nd Stan Imhulse 2002-03 3rd - 6th Warren Mandrell 1966-67 2nd - 1st Stan Imhulse 1967-68 1st - 3rd Stan Imhulse 2003-04 3rd - 4th Warren Mandrell 1968-69 2nd - 4th Stan Imhulse 2004-05 2nd - 4th Warren Mandrell 1969-70 3rd - 3rd Stan Imhulse 2005-06 2nd - 5th Warren Mandrell 1970-71 4th - 3rd Chuck Zody 2006-07 4th -

Lesson Plans Introduction the Following Section Provides Twenty-Seven Ready-To-Implement Lesson Plans for Teachers
Lesson Plans Introduction The following section provides twenty-seven ready-to-implement lesson plans for teachers. The section is divided into four smaller sub-sections. • Early Stage 1 (5 year olds) • Stage 1 (6/7 year olds) • Stage 2 (8/9 year olds) • Stage 3 (10 years and LAANSWabove) ASAP Level 3 Each sub-section contains lesson plans suitable for children in these age groups. The lesson plans assume classes of up to thirty students and a time limit of 30-45 minutes, however a teacher can adapt the ideas to suit their particular circumstances. Each lesson plan generally follows the same format, being: Aim; Equipment; Warm Up; Skill Development; Games. In relevant places, topics such as safety aspects and various hints that will help the teacher organise and conduct a successful lesson are included. The lesson plans at times assume prior learning, ie. that the children have participated in the skill development activities contained in preceding lessons designed for the earlier levels. The activities featured in the lesson plans are based on fun, skill development, maximum group participation and a sound, logical progression. The lesson plans form the foundation of a class athletics unit. 3 29 Early Stage 1 Lesson Plans • Running - Lesson 1 - Lesson 2 • Jumping - Lesson 1 - LessonLAANSW 2 ASAP Level 3 • Throwing - Lesson 1 - Lesson 2 30 Early Stage 1 Running Lesson Plan Lesson 1 Introduction to basic running technique Introduction to relays Ground markers x 30 Relay batons x 5 Warm Up 1. Group Game: "Signals" LAANSW ASAP Level 3 Set up a playing area with ground markers. -

Mtrack 1-13.Indd
NCAA STANDARDS/QUICKMEET THE BRUINS FACTS ‘09 TRACK/FIELD 2009 NCAA INDOOR CHAMPIONSHIP 2009 NCAA WEST REGION TABLE OF CONTENTS QUALIFYING STANDARDS QUALIFYING STANDARDS GENERAL INFORMATION .................................1 EVENT AUTOMATIC PROVISIONAL EVENT QUALIFYING MARK Qualifying Standards.................................................................... 1 55m 6.14 6.25 100m 10.55 Quick Facts .......................................................................................1 60m 6.63 6.74 200m 21.35 Schedule ........................................................................Back Cover 55m Hurdles 7.17 7.38 400m 47.20 Support Staff .................................................................................10 60m Hurdles 7.70 7.91 800m 1:50.40 Media Information ......................................................................11 200m 20.83 21.23 1500m 3:47.80 Facility Information .....................................................................12 400m 46.15 47.25 Mile# 4:06.00 800m 1:48.00 1:50.50 3000m Steeplechase# 9:07.00 Mile 3:59.50 4:04.00 5000m# 14:12.00 THE 2009 SEASON ......................................... 2 Roster ................................................................................................. 2 3000m 7:54.50 8:05.00 110m Hurdles 14.30 Pronunciation Guide .................................................................... 2 5000m 13:47.00 14:10.00 400m Hurdles 52.51 Season Outlook ..............................................................................3 1600m Relay 3:06.50 -

2021 Track & Field Record Book
2021 TRACK & FIELD RECORD BOOK 1 Mondo broke his own world record with a clearance of 6.18 meters in Glasgow, Scotland, on February 15, 2020. 2020 World Athletics Male Athlete of the Year Baton Rouge, La. – Mondo Duplantis was named Renaud Lavilennie’s previous world record of 6.14 Greg, were given the Coaching Achievement Award. the winner of the 2020 World Athletics Male Athlete of meters that was set in 2014. Helena and Greg serve as Mondo’s coaches and the Year award on December 5, 2020. The virtual cer- It was only a week later and he re-upped his world training advisors; Greg still serves as a volunteer emony announced a plethora of awards in what was a record by a centimeter with a clearance of 6.18 meters assistant coach with the LSU track and field program. celebration of the sport of track and field. on February 15 at the Muller Indoor Grand Prix in Mondo also was part of an award that was won by Mondo won the award over Joshua Cheptegei Glasgow. The indoor season saw him compete five Renaud Lavillenie – the COVID Inspiration award. In the (Uganda), Ryan Crouser (USA), Johannes Vetter times and at each event he cleared six meters or early stages of COVID-19 lockdowns, Lavillenie came (Germany), and Karsten Warholm (Norway). Duplantis, higher. up with the concept of the ‘Ultimate Garden Clash’. It who is 21 years old, becomes the youngest winner of Following a three and a half month hiatus due was event that three pole vaulters – Lavillenie, Mondo, this award. -

Athletics Sport Rules
ATHLETICS SPORT RULES Athletics Sport Rules 1 VERSION: June 2018 © Special Olympics, Inc., 2018 All rights reserved ATHLETICS SPORT RULES TABLE OF CONTENTS 1. GOVERNING RULES ................................................................................................................................. 5 2. OFFICIAL EVENTS.................................................................................................................................... 5 Track Events ................................................................................................................................... 5 25 Meters ........................................................................................................................... 5 50 Meters ........................................................................................................................... 5 100 Meters ......................................................................................................................... 5 200 Meters ......................................................................................................................... 5 400 Meters ......................................................................................................................... 5 800 Meters ......................................................................................................................... 5 1500 Meters ....................................................................................................................... 5 3000 Meters -

Biological Determinants of Track and Field Throwing Performance
Journal of Functional Morphology and Kinesiology Review Biological Determinants of Track and Field Throwing Performance Nikolaos Zaras 1,*, Angeliki-Nikoletta Stasinaki 2 and Gerasimos Terzis 2 1 Human Performance Laboratory, Department of Life and Health Sciences, University of Nicosia, Nicosia 1700, Cyprus 2 Sports Performance Laboratory, School of Physical Education and Sport Science, University of Athens, 17237 Athens, Greece; [email protected] (A.-N.S.); [email protected] (G.T.) * Correspondence: [email protected]; Tel.: +357-22842318; Fax: +357-22842399 Abstract: Track and field throwing performance is determined by a number of biomechanical and biological factors which are affected by long-term training. Although much of the research has focused on the role of biomechanical factors on track and field throwing performance, only a small body of scientific literature has focused on the connection of biological factors with competitive track and field throwing performance. The aim of this review was to accumulate and present the current literature connecting the performance in track and field throwing events with specific biological factors, including the anthropometric characteristics, the body composition, the neural activation, the fiber type composition and the muscle architecture characteristics. While there is little published information to develop statistical results, the results from the current review suggest that major biological determinants of track and field throwing performance are the size of lean body mass, the neural activation of the protagonist muscles during the throw and the percentage of type II muscle fiber cross-sectional area. Long-term training may enhance these biological factors and possibly Citation: Zaras, N.; Stasinaki, A.-N.; lead to a higher track and field throwing performance. -

OSAA Boys Track & Field Championships
OSAA Boys Track & Field Championships 4A Individual State Champions Through 2006 100-METER DASH 1992 Seth Wetzel, Jesuit ............................................ 1:53.20 1978 Byron Howell, Central Catholic................................. 10.5 1993 Jon Ryan, Crook County ..................................... 1:52.44 300-METER INTERMEDIATE HURDLES 1979 Byron Howell, Central Catholic............................... 10.67 1994 Jon Ryan, Crook County ..................................... 1:54.93 1978 Rourke Lowe, Aloha .............................................. 38.01 1980 Byron Howell, Central Catholic............................... 10.64 1995 Bryan Berryhill, Crater ....................................... 1:53.95 1979 Ken Scott, Aloha .................................................. 36.10 1981 Kevin Vixie, South Eugene .................................... 10.89 1996 Bryan Berryhill, Crater ....................................... 1:56.03 1980 Jerry Abdie, Sunset ................................................ 37.7 1982 Kevin Vixie, South Eugene .................................... 10.64 1997 Rob Vermillion, Glencoe ..................................... 1:55.49 1981 Romund Howard, Madison ....................................... 37.3 1983 John Frazier, Jefferson ........................................ 10.80w 1998 Tim Meador, South Medford ............................... 1:55.21 1982 John Elston, Lebanon ............................................ 39.02 1984 Gus Envela, McKay............................................. 10.55w 1999 -
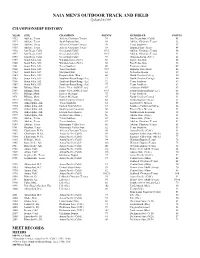
NAIA MEN's OUTDOOR TRACK and FIELD Updated 6/1/09
NAIA MEN'S OUTDOOR TRACK AND FIELD Updated 6/1/09 CHAMPIONSHIP HISTORY YEAR SITE CHAMPION POINTS RUNNER-UP POINTS 1952 Abilene, Texas Abilene Christian (Texas) 74 San Diego State (Calif.) 45 1953 Abilene, Texas South Dakota State 48 Abilene Christian (Texas) 42 1954 Abilene, Texas Abilene Christian (Texas) 39 Texas Southern 33 1955 Abilene, Texas Abilene Christian (Texas) 68 Emporia State (Kan.) 44 1956 San Diego, Calif. Occidental (Calif.) 89.5 Abilene Christian (Texas) 56 1957 San Diego, Calif. Occidental (Calif.) 148.5 Abilene Christian (Texas) 34 1958 San Diego, Calif. Occidental (Calif.) 93 Winston-Salem (N.C.) 62 1959 Sioux Falls, S.D. Winston-Salem (N.C.) 56 East Texas State 55 1960 Sioux Falls, S.D. Winston-Salem (N.C.) 58 East Texas State 45 1961 Sioux Falls, S.D. Texas Southern 49 Tennessee State 47 1962 Sioux Falls, S.D. Texas Southern 72.5 Emporia State (Kan.) 46 1963 Sioux Falls, S.D. Maryland State 82 Nebraska-Omaha 33 1964 Sioux Falls, S.D. Emporia State (Kan.) 60 North Carolina College 50 1965 Sioux Falls, S.D. Southern-Baton Rouge (La.) 77 North Carolina College 40 1966 Sioux Falls, S.D. Southern-Baton Rouge (La.) 92 Texas Southern 69 1967 Sioux Falls, S.D. Southern-Baton Rouge (La.) 77 Texas Southern 63 1968 Billings, Mont. Prairie View A&M (Texas) 47 Arkansas AM&N 45 1969 Billings, Mont. Prairie View A&M (Texas) 69.5 Southern-Baton Rouge (La.) 68 1970 Billings, Mont. Eastern Michigan 75 Texas Southern 50 1971 Billings, Mont. Eastern Michigan 65 North Carolina Central 43 1972 Billings, Mont. -

Hypo Vorarlberg Geschichte Hypomeeting Bis 2019
45 Jahre Leichtathletik-Geschichte Hypomeeting Götzis / Vorarlberg 1974 In diesem Jahr hat sich die LG Montfort entschieden, sich für die Durchführung der Österrei- chischen Mehrkampfmeisterschaften zu bewerben. Die im Juli 1973 durchgeführten Mehr- kampfmeisterschaften brachten neben dem großartigen österreichischen Rekord von Sepp Zeilbauer mit genau 8000 Punkten eine beachtliche Zuschauerresonanz. Die einen Monat später in Innsbruck ausgetragene Vorrunde im Mehrkampf-Europacup (Sepp Zeilbauer begeisterte wiederum mit neuem Rekord) brachte Armin Hug, Konrad Lerch, Elmar Oberhauser und Werner Ströhle auf den Gedanken, anstelle des nicht mehr durchgeführten traditionellen Mehrkampfmeetings in Schielleiten eine entsprechende internationale Veran- staltung im Mösle-Stadion abzuwickeln. Die vielen internationalen Kontakte von ÖLV-Mehr- kamptrainer Konrad Lerch zu seinen Trainerkollegen und AthletInnen sollte dabei die Basis für attraktive Startfelder bilden. 1975 Trotz widrigster Wetterverhältnisse (Regen und Kälte) gab es eine Jahresweltbestleistung von Burglinde Pollak/DDR im 5-Kampf und einen tschechischen Sieg im 10-Kampf durch Petr Kratky. Große Begeisterung der Athleten und Mannschaftsführer über die Organisation und die herzliche Atmosphäre, sowie ein kräfti- ger finanzieller Abgang kennzeichneten das erste Meeting. 1976 Die Volksbank konnte als Sponsor gewonnen werden, Subven- tionszusagen von Bund, Land und Marktgemeinde Götzis, sowie vom ASVÖ veranlassten die Initiatoren des Meetings Luis Fessler, Armin Hug, Konrad Lerch, Elmar Oberhauser und Werner Ströhle zu einem neuerlichen Versuch. Im Zehnkampf siegte mit Jahresweltbestleistung und neuem deutschem Rekord von 8.381 Punkten (8.302 Punktetabelle 1985) Guido Kratschmer vor dem mit 8.310 Punkten (8.219) österreichi- schen Rekord erzielenden Sepp Zeilbauer. Im Fünfkampf feier- te Diane Jones/Kanada einen sehr knappen Sieg (6 Punkte) vor Burglinde Pollak. -

Men's Track & Field Naia Nat'l Competitors
MEN'S TRACK & FIELD NAIA NAT'L COMPETITORS ATHLETE EVENT YEAR ERIC ADE Outdoor 3000 M Steeplechase 2000 MICHAEL ANKROM Outdoor Triple Jump 1987 JIM ARNETT Indoor Shot Put 1995, 1996, 1997, 1998 Indoor Weight Throw 1996, 1997, 1998 Outdoor Discus 1995, 1996, 1997, 1998 Outdoor Shot Put 1995, 1996, 1997, 1998 KAM BAILEY Outdoor 200 Meters 2009 LUCAS BEACH Indoor Shot Put 2006, 2007, 2008, 2009 Outdoor Hammer 2009 Outdoor Shot Put 2006, 2007, 2008, 2009 PAUL BOWERS Outdoor 110 M Hurdles 1989 AARON CHASTAIN Outdoor Hammer 1991 Outdoor Shot Put 1990, 1991 ELIJAH CHESTERMAN Outdoor 4x800 M Relay 2019 Indoor 4x800 M Relay 2020 Indoor Distance Medley Relay 2020 DANIEL DEBONI Outdoor 100 Meters 2014 Outdoor 200 Meters 2014 PEYTON DEPRIEST Indoor Distance Medley Relay 2020 LUKE DIEHL Outdoor 3000 M Steeplechase 2008, 2009, 2010 Outdoor 4x800 M Relay 2007 BEAU DOWDEN Outdoor 5000 M Walk 1998 JONATHAN DOYLE Indoor 55 M Hurdles 2002, 2004 Outdoor 110 M Hurdles 2004 Outdoor 400 M Hurdles 2003, 2004 KAI FODAY Outdoor Javelin 2016 ADRIEN GENTIE Indoor Mile 2019 Outdoor 4x800 M Relay 2019 Indoor 4x800 M Relay 2020 Indoor Distance Medley Relay 2020 BROOKS GERKE Indoor Heptathlon 2015, 2017 Outdoor Pole Vault 2018 MATTHIAS HALLER Indoor 800 Meters 2009 Outdoor 800 Meters 2009 RICK HAMMER Indoor 3000 Meters 2002 CODY HANNIE Indoor 800 Meters 2006 Indoor 1000 Meters 2004, 2007 Indoor 3000 Meters 2005 Outdoor 4x800 M Relay 2007 AARON HENDRYX Indoor 4x800 M Relay 2020 JOSEPH HERBER Indoor 3000 Meters 2009 Indoor 5000 Meters 2011, 2012 Outdoor 10,000 Meters -

12 Years and Under Track and Field Championships Records
Current at December 2016 12 YEARS AND UNDER TRACK AND FIELD CHAMPIONSHIPS RECORDS DECEMBER 2016 BOYS 100m 10 years David Kim NSW 1998 12.63 11 years Robert Boateng NSW 1998 11.97 12 years Bright Appiah NSW 2008 11.62 200m 10 years Hafiz Gami NSW 2006 26.43 11 years Alex Jalloh NSW 2006 24.43 12 years Bright Appiah NSW 2008 23.55 800m 10 years Andrew O’Neill NSW 1993 2: 15.62 11 years Benjamin Ganko QLD 2012 2:10.66 12 years Zane Palmer QLD 1997 2:05.61 High Jump 10 years A Graham NSW 1995 1.59m 11 years S Hingston-Curtis QLD 1990 1.70m 12 years Joseph Suaalii NSW 2015 1.78m Long Jump 10 years Michael Orchard VIC 1986 5.21m 11 years Paul Di Bella QLD 1988 5.54m 12 years W Smart QLD 1998 5.92m Shot Put 10 years Latham Takau QLD 2005 14.43m (2kg) 11 years Scott Travena QLD 2010 16.71m (2kg) 12 years Latham Takau QLD 2007 16.50m (3kg) Discus 10 years Mitchell Cooper QLD 2005 43.28m 11 years Jamal Idris NSW 2001 42.93m 12 years Lukas Ripley QLD 2014 58.31m Multi Event (100m, Long Jump, Shot Put, 800m) 10 Years Keny Arcangeli QLD 2006 1266 Points 11 Years Ezraa Coulston QLD 2012 1423 Points 12 Years Sam Hegarty QLD 2004 1540 Points Medley Relay (200m, 200m, 100m, 300m) 10 Years New South Wales 2016 1:53.32 11 Years Victoria 2013 1:49.93 12 Years Victoria 2013 1:45.19 4 x 100m Relay 10 years Queensland 1987 52.10 11 years New South Wales 2006 49.93 12 years Queensland 200 8 46.19 12 YEARS AND UNDER TRACK AND FIELD CHAMPIONSHIPS RECORDS DECEMBER 2016 GIRLS 100m 10 years Charlotte Van Veenendaal NSW 1998 13.02 11 years Hayley Malt VIC 1998 12.50