Roots of Complex Numbers

Total Page：16

File Type：pdf, Size：1020Kb

Lecture 5: Roots of Complex Numbers Dan Sloughter Furman University Mathematics 39 March 14, 2004 5.1 Roots Suppose z0 is a complex number and, for some positive integer n, z is an nth n iθ iθ0 root of z0; that is, z = z0. Now if z = re and z0 = r0e , then we must have n r = r0 and nθ = θ0 + 2kπ for some integer k. Hence we must have √ n r = r0, √ n where r0 denotes the unique positive nth root of the real number r, and θ 2kπ θ = 0 + n n for some integer k. Hence the numbers √ θ 2kπ z = n r exp i 0 + , for k = 0, ±1, ±2,..., 0 n n are all nth roots of z0, with √ θ 2kπ z = n r exp i 0 + , for k = 0, 1, 2, . , n − 1, 0 n n 1 1 n being the n distinct nth roots of z0. We let z0 denote this set of nth roots of√ z0. Note that these roots are equally spaced around the circle of radius n r0. If θ0 = Arg z0, we call √ θ n i 0 z = r0e n , the principal root of z0. 5.2 Roots of unity Example 5.1. Since 1 = 1ei(0+2kπ) for k = 0, ±1, ±2,..., for any positive integer n, i 2kπ z = e n is an nth root of 1 for any integer k, which we call an nth root of unity. If we let i 2π ωn = e n , then, for any integer k, 2kπ k i n ωn = e Hence the distinct nth roots of unity are 2 n−1 1, ωn, ωn, . , ωn . For example, when n = 2, iπ ω2 = e = −1, and the roots of unity are simply 1 and −1. When n = 3, i 2π w3 = e 3 , and the distinct third roots of unity are i 2π i 4π 1, e 3 , e 3 ; that is √ √ 1 3 1 3 1, − + i, − − i. 2 2 2 2 2 1 0.5 -1 -0.5 0.5 1 -0.5 -1 Figure 5.1: The third roots of unity form an equilateral triangle When n = 4, i 2π i π ω4 = e 4 = e 2 = i, and the distinct roots fourth roots of unity are 1, i, −1, −i. Note that the nth roots of unity are equally spaced around the unit circle. For example, the third roots of unity form an equilateral triangle in the unit circle, as shown in Figure 5.1. More generally, if c is any particular nth root of z0, then the distinct nth roots of z0 are 2 n−1 c, cωn, cωn, . , cωn . Example 5.2. To ﬁnd the cube roots of −27i, we ﬁrst note that π −27i = 27 exp i − + 2kπ , for k = 0, ±1, ±2,.... 2 3 3 2 1 -3 -2 -1 1 2 3 -1 -2 -3 Figure 5.2: The cube roots of −27i form an equilateral triangle Hence the principal cube root of −27i is √ −i π π π 3 3 3 c = 3e 6 = 3 cos − i sin = − i. 0 6 6 2 2 The remaining cube roots are i π π π c = 3e 2 = 3 cos + i sin = 3i, 1 2 2 and √ i 7π 7π 7π 3 3 3 c = 3e 6 = 3 cos + i sin = − − i, 2 6 6 2 2 2 which are simply c0ω3 and c0ω3, where i 2π ω3 = e 3 . 4.

Copy Link

Recommended publications

A Quartically Convergent Square Root Algorithm: an Exercise in Forensic Paleo-Mathematics
A Quartically Convergent Square Root Algorithm: An Exercise in Forensic Paleo-Mathematics David H Bailey, Lawrence Berkeley National Lab, USA DHB’s website: http://crd.lbl.gov/~dhbailey! Collaborator: Jonathan M. Borwein, University of Newcastle, Australia 1 A quartically convergent algorithm for Pi: Jon and Peter Borwein’s first “big” result In 1985, Jonathan and Peter Borwein published a “quartically convergent” algorithm for π. “Quartically convergent” means that each iteration approximately quadruples the number of correct digits (provided all iterations are performed with full precision): Set a0 = 6 - sqrt[2], and y0 = sqrt[2] - 1. Then iterate: 1 (1 y4)1/4 y = − − k k+1 1+(1 y4)1/4 − k a = a (1 + y )4 22k+3y (1 + y + y2 ) k+1 k k+1 − k+1 k+1 k+1 Then ak, converge quartically to 1/π. This algorithm, together with the Salamin-Brent scheme, has been employed in numerous computations of π. Both this and the Salamin-Brent scheme are based on the arithmetic-geometric mean and some ideas due to Gauss, but evidently he (nor anyone else until 1976) ever saw the connection to computation. Perhaps no one in the pre-computer age was accustomed to an “iterative” algorithm? Ref: J. M. Borwein and P. B. Borwein, Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity}, John Wiley, New York, 1987. 2 A quartically convergent algorithm for square roots I have found a quartically convergent algorithm for square roots in a little-known manuscript: · To compute the square root of q, let x0 be the initial approximation.
[Show full text]
Solving Cubic Polynomials
Solving Cubic Polynomials 1.1 The general solution to the quadratic equation There are four steps to ﬁnding the zeroes of a quadratic polynomial. 1. First divide by the leading term, making the polynomial monic. a 2. Then, given x2 + a x + a , substitute x = y − 1 to obtain an equation without the linear term. 1 0 2 (This is the \depressed" equation.) 3. Solve then for y as a square root. (Remember to use both signs of the square root.) a 4. Once this is done, recover x using the fact that x = y − 1 . 2 For example, let's solve 2x2 + 7x − 15 = 0: First, we divide both sides by 2 to create an equation with leading term equal to one: 7 15 x2 + x − = 0: 2 2 a 7 Then replace x by x = y − 1 = y − to obtain: 2 4 169 y2 = 16 Solve for y: 13 13 y = or − 4 4 Then, solving back for x, we have 3 x = or − 5: 2 This method is equivalent to \completing the square" and is the steps taken in developing the much- memorized quadratic formula. For example, if the original equation is our \high school quadratic" ax2 + bx + c = 0 then the ﬁrst step creates the equation b c x2 + x + = 0: a a b We then write x = y − and obtain, after simplifying, 2a b2 − 4ac y2 − = 0 4a2 so that p b2 − 4ac y = ± 2a and so p b b2 − 4ac x = − ± : 2a 2a 1 The solutions to this quadratic depend heavily on the value of b2 − 4ac.
[Show full text]
Algebraic Number Theory
Algebraic Number Theory William B. Hart Warwick Mathematics Institute Abstract. We give a short introduction to algebraic number theory. Algebraic number theory is the study of extension fields Q(α1; α2; : : : ; αn) of the rational numbers, known as algebraic number fields (sometimes number fields for short), in which each of the adjoined complex numbers αi is algebraic, i.e. the root of a polynomial with rational coefficients. Throughout this set of notes we use the notation Z[α1; α2; : : : ; αn] to denote the ring generated by the values αi. It is the smallest ring containing the integers Z and each of the αi. It can be described as the ring of all polynomial expressions in the αi with integer coefficients, i.e. the ring of all expressions built up from elements of Z and the complex numbers αi by finitely many applications of the arithmetic operations of addition and multiplication. The notation Q(α1; α2; : : : ; αn) denotes the field of all quotients of elements of Z[α1; α2; : : : ; αn] with nonzero denominator, i.e. the field of rational functions in the αi, with rational coefficients. It is the smallest field containing the rational numbers Q and all of the αi. It can be thought of as the field of all expressions built up from elements of Z and the numbers αi by finitely many applications of the arithmetic operations of addition, multiplication and division (excepting of course, divide by zero). 1 Algebraic numbers and integers A number α 2 C is called algebraic if it is the root of a monic polynomial n n−1 n−2 f(x) = x + an−1x + an−2x + ::: + a1x + a0 = 0 with rational coefficients ai.
[Show full text]
Chapter 5 Complex Numbers
Chapter 5 Complex numbers Why be one-dimensional when you can be two-dimensional? ? 3 2 1 0 1 2 3 − − − ? We begin by returning to the familiar number line, where I have placed the question marks there appear to be no numbers. I shall rectify this by defining the complex numbers which give us a number plane rather than just a number line. Complex numbers play a fundamental rôlein mathematics. In this chapter, I shall use them to show how e and π are connected and how certain primes can be factorized. They are also fundamental to physics where they are used in quantum mechanics. 5.1 Complex number arithmetic In the set of real numbers we can add, subtract, multiply and divide, but we cannot always extract square roots. For example, the real number 1 has 125 126 CHAPTER 5. COMPLEX NUMBERS the two real square roots 1 and 1, whereas the real number 1 has no real square roots, the reason being that− the square of any real non-zero− number is always positive. In this section, we shall repair this lack of square roots and, as we shall learn, we shall in fact have achieved much more than this. Com- plex numbers were first studied in the 1500’s but were only fully accepted and used in the 1800’s. Warning! If r is a positive real number then √r is usually interpreted to mean the positive square root. If I want to emphasize that both square roots need to be considered I shall write √r.
[Show full text]
The Nth Root of a Number Page 1
Lecture Notes The nth Root of a Number page 1 Caution! Currently, square roots are dened differently in different textbooks. In conversations about mathematics, approach the concept with caution and rst make sure that everyone in the conversation uses the same denition of square roots. Denition: Let A be a non-negative number. Then the square root of A (notation: pA) is the non-negative number that, if squared, the result is A. If A is negative, then pA is undened. For example, consider p25. The square-root of 25 is a number, that, when we square, the result is 25. There are two such numbers, 5 and 5. The square root is dened to be the non-negative such number, and so p25 is 5. On the other hand, p 25 is undened, because there is no real number whose square, is negative. Example 1. Evaluate each of the given numerical expressions. a) p49 b) p49 c) p 49 d) p 49 Solution: a) p49 = 7 c) p 49 = unde ned b) p49 = 1 p49 = 1 7 = 7 d) p 49 = 1 p 49 = unde ned Square roots, when stretched over entire expressions, also function as grouping symbols. Example 2. Evaluate each of the following expressions. a) p25 p16 b) p25 16 c) p144 + 25 d) p144 + p25 Solution: a) p25 p16 = 5 4 = 1 c) p144 + 25 = p169 = 13 b) p25 16 = p9 = 3 d) p144 + p25 = 12 + 5 = 17 . Denition: Let A be any real number. Then the third root of A (notation: p3 A) is the number that, if raised to the third power, the result is A.
[Show full text]
Math Symbol Tables
APPENDIX A I Math symbol tables A.I Hebrew letters Type: Print: Type: Print: \aleph ~ \beth :J \daleth l \gimel J All symbols but \aleph need the amssymb package. 346 Appendix A A.2 Greek characters Type: Print: Type: Print: Type: Print: \alpha a \beta f3 \gamma 'Y \digamma F \delta b \epsilon E \varepsilon E \zeta ( \eta 'f/ \theta () \vartheta {) \iota ~ \kappa ,.. \varkappa x \lambda ,\ \mu /-l \nu v \xi ~ \pi 7r \varpi tv \rho p \varrho (} \sigma (J \varsigma <; \tau T \upsilon v \phi ¢ \varphi 'P \chi X \psi 'ljJ \omega w \digamma and \ varkappa require the amssymb package. Type: Print: Type: Print: \Gamma r \varGamma r \Delta L\ \varDelta L.\ \Theta e \varTheta e \Lambda A \varLambda A \Xi ~ \varXi ~ \Pi II \varPi II \Sigma 2: \varSigma E \Upsilon T \varUpsilon Y \Phi <I> \varPhi t[> \Psi III \varPsi 1ft \Omega n \varOmega D All symbols whose name begins with var need the amsmath package. Math symbol tables 347 A.3 Y1EX binary relations Type: Print: Type: Print: \in E \ni \leq < \geq >'" \11 « \gg \prec \succ \preceq \succeq \sim \cong \simeq \approx \equiv \doteq \subset c \supset \subseteq c \supseteq \sqsubseteq c \sqsupseteq \smile \frown \perp 1- \models F \mid I \parallel II \vdash f- \dashv -1 \propto <X \asymp \bowtie [Xl \sqsubset \sqsupset \Join The latter three symbols need the latexsym package. 348 Appendix A A.4 AMS binary relations Type: Print: Type: Print: \leqs1ant :::::; \geqs1ant ): \eqs1ant1ess :< \eqs1antgtr :::> \lesssim < \gtrsim > '" '" < > \lessapprox ~ \gtrapprox \approxeq ~ \lessdot <:: \gtrdot Y \111 «< \ggg »> \lessgtr S \gtr1ess Z < >- \lesseqgtr > \gtreq1ess < > < \gtreqq1ess \lesseqqgtr > < ~ \doteqdot --;- \eqcirc = .2..
[Show full text]
Number Theory and Graph Theory Chapter 3 Arithmetic Functions And
1 Number Theory and Graph Theory Chapter 3 Arithmetic functions and roots of unity By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: [email protected] 2 Module-4: nth roots of unity Objectives • Properties of nth roots of unity and primitive nth roots of unity. • Properties of Cyclotomic polynomials. Deﬁnition 1. Let n 2 N. Then, a complex number z is called 1. an nth root of unity if it satisﬁes the equation xn = 1, i.e., zn = 1. 2. a primitive nth root of unity if n is the smallest positive integer for which zn = 1. That is, zn = 1 but zk 6= 1 for any k;1 ≤ k ≤ n − 1. 2pi zn = exp( n ) is a primitive n-th root of unity. k • Note that zn , for 0 ≤ k ≤ n − 1, are the n distinct n-th roots of unity. • The nth roots of unity are located on the unit circle of the complex plane, and in that plane they form the vertices of an n-sided regular polygon with one vertex at (1;0) and centered at the origin. The following points are collected from the article Cyclotomy and cyclotomic polynomials by B.Sury, Resonance, 1999. 1. Cyclotomy - literally circle-cutting - was a puzzle begun more than 2000 years ago by the Greek geometers. In their pastime, they used two implements - a ruler to draw straight lines and a compass to draw circles. 2. The problem of cyclotomy was to divide the circumference of a circle into n equal parts using only these two implements.
[Show full text]
Monic Polynomials in $ Z [X] $ with Roots in the Unit Disc
MONIC POLYNOMIALS IN Z[x] WITH ROOTS IN THE UNIT DISC Pantelis A. Damianou A Theorem of Kronecker This note is motivated by an old result of Kronecker on monic polynomials with integer coefficients having all their roots in the unit disc. We call such polynomials Kronecker polynomials for short. Let k(n) denote the number of Kronecker polynomials of degree n. We describe a canonical form for such polynomials and use it to determine the sequence k(n), for small values of n. The first step is to show that the number of Kronecker polynomials of degree n is finite. This fact is included in the following theorem due to Kronecker [6]. See also [5] for a more accessible proof. The theorem actually gives more: the non-zero roots of such polynomials are on the boundary of the unit disc. We use this fact later on to show that these polynomials are essentially products of cyclotomic polynomials. Theorem 1 Let λ =06 be a root of a monic polynomial f(z) with integer coefficients. If all the roots of f(z) are in the unit disc {z ∈ C ||z| ≤ 1}, then |λ| =1. Proof Let n = degf. The set of all monic polynomials of degree n with integer coefficients having all their roots in the unit disc is finite. To see this, we write n n n 1 n 2 z + an 1z − + an 2z − + ··· + a0 = (z − zj) , − − j Y=1 where aj ∈ Z and zj are the roots of the polynomial. Using the fact that |zj| ≤ 1 we have: n |an 1| = |z1 + z2 + ··· + zn| ≤ n = − 1 n |an 2| = | zjzk| ≤ − j,k 2! .
[Show full text]
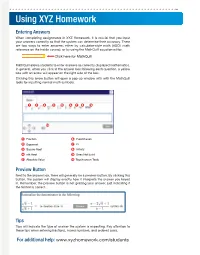
Using XYZ Homework
Using XYZ Homework Entering Answers When completing assignments in XYZ Homework, it is crucial that you input your answers correctly so that the system can determine their accuracy. There are two ways to enter answers, either by calculator-style math (ASCII math reference on the inside covers), or by using the MathQuill equation editor. Click here for MathQuill MathQuill allows students to enter answers as correctly displayed mathematics. In general, when you click in the answer box following each question, a yellow box with an arrow will appear on the right side of the box. Clicking this arrow button will open a pop-up window with with the MathQuill tools for inputting normal math symbols. 1 2 3 4 5 6 7 8 9 10 1 Fraction 6 Parentheses 2 Exponent 7 Pi 3 Square Root 8 Inﬁnity 4 nth Root 9 Does Not Exist 5 Absolute Value 10 Touchscreen Tools Preview Button Next to the answer box, there will generally be a preview button. By clicking this button, the system will display exactly how it interprets the answer you keyed in. Remember, the preview button is not grading your answer, just indicating if the format is correct. Tips Tips will indicate the type of answer the system is expecting. Pay attention to these tips when entering fractions, mixed numbers, and ordered pairs. For additional help: www.xyzhomework.com/students ASCII Math (Calculator Style) Entry Some question types require a mathematical expression or equation in the answer box. Because XYZ Homework follows order of operations, the use of proper grouping symbols is necessary.
[Show full text]
A Historical Survey of Methods of Solving Cubic Equations Minna Burgess Connor
University of Richmond UR Scholarship Repository Master's Theses Student Research 7-1-1956 A historical survey of methods of solving cubic equations Minna Burgess Connor Follow this and additional works at: http://scholarship.richmond.edu/masters-theses Recommended Citation Connor, Minna Burgess, "A historical survey of methods of solving cubic equations" (1956). Master's Theses. Paper 114. This Thesis is brought to you for free and open access by the Student Research at UR Scholarship Repository. It has been accepted for inclusion in Master's Theses by an authorized administrator of UR Scholarship Repository. For more information, please contact [email protected]. A HISTORICAL SURVEY OF METHODS OF SOLVING CUBIC E<~UATIONS A Thesis Presented' to the Faculty or the Department of Mathematics University of Richmond In Partial Fulfillment ot the Requirements tor the Degree Master of Science by Minna Burgess Connor August 1956 LIBRARY UNIVERStTY OF RICHMOND VIRGlNIA 23173 - . TABLE Olf CONTENTS CHAPTER PAGE OUTLINE OF HISTORY INTRODUCTION' I. THE BABYLONIANS l) II. THE GREEKS 16 III. THE HINDUS 32 IV. THE CHINESE, lAPANESE AND 31 ARABS v. THE RENAISSANCE 47 VI. THE SEVEW.l'EEl'iTH AND S6 EIGHTEENTH CENTURIES VII. THE NINETEENTH AND 70 TWENTIETH C:BNTURIES VIII• CONCLUSION, BIBLIOGRAPHY 76 AND NOTES OUTLINE OF HISTORY OF SOLUTIONS I. The Babylonians (1800 B. c.) Solutions by use ot. :tables II. The Greeks·. cs·oo ·B.c,. - )00 A~D.) Hippocrates of Chios (~440) Hippias ot Elis (•420) (the quadratrix) Archytas (~400) _ .M~naeobmus J ""375) ,{,conic section~) Archimedes (-240) {conioisections) Nicomedea (-180) (the conchoid) Diophantus ot Alexander (75) (right-angled tr~angle) Pappus (300) · III.
[Show full text]
Finite Fields: Further Properties
Chapter 4 Finite fields: further properties 8 Roots of unity in finite fields In this section, we will generalize the concept of roots of unity (well-known for complex numbers) to the finite field setting, by considering the splitting field of the polynomial xn − 1. This has links with irreducible polynomials, and provides an effective way of obtaining primitive elements and hence representing finite fields. Definition 8.1 Let n ∈ N. The splitting field of xn − 1 over a field K is called the nth cyclotomic field over K and denoted by K(n). The roots of xn − 1 in K(n) are called the nth roots of unity over K and the set of all these roots is denoted by E(n). The following result, concerning the properties of E(n), holds for an arbitrary (not just a finite!) field K. Theorem 8.2 Let n ∈ N and K a field of characteristic p (where p may take the value 0 in this theorem). Then (i) If p ∤ n, then E(n) is a cyclic group of order n with respect to multiplication in K(n). (ii) If p | n, write n = mpe with positive integers m and e and p ∤ m. Then K(n) = K(m), E(n) = E(m) and the roots of xn − 1 are the m elements of E(m), each occurring with multiplicity pe. Proof. (i) The n = 1 case is trivial. For n ≥ 2, observe that xn − 1 and its derivative nxn−1 have no common roots; thus xn −1 cannot have multiple roots and hence E(n) has n elements.
[Show full text]
The Evolution of Equation-Solving: Linear, Quadratic, and Cubic
California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2006 The evolution of equation-solving: Linear, quadratic, and cubic Annabelle Louise Porter Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Porter, Annabelle Louise, "The evolution of equation-solving: Linear, quadratic, and cubic" (2006). Theses Digitization Project. 3069. https://scholarworks.lib.csusb.edu/etd-project/3069 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. THE EVOLUTION OF EQUATION-SOLVING LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degre Master of Arts in Teaching: Mathematics by Annabelle Louise Porter June 2006 THE EVOLUTION OF EQUATION-SOLVING: LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino by Annabelle Louise Porter June 2006 Approved by: Shawnee McMurran, Committee Chair Date Laura Wallace, Committee Member , (Committee Member Peter Williams, Chair Davida Fischman Department of Mathematics MAT Coordinator Department of Mathematics ABSTRACT Algebra and algebraic thinking have been cornerstones of problem solving in many different cultures over time. Since ancient times, algebra has been used and developed in cultures around the world, and has undergone quite a bit of transformation. This paper is intended as a professional developmental tool to help secondary algebra teachers understand the concepts underlying the algorithms we use, how these algorithms developed, and why they work.
[Show full text]