How to Use Origami to Solve Problems in Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mathematics of Origami
Mathematics of Origami Angela Kohlhaas Loras College February 17, 2012 Introduction Origami ori + kami, “folding paper” Tools: one uncut square of paper, mountain and valley folds Goal: create art with elegance, balance, detail Outline History Applications Foldability Design History of Origami 105 A.D.: Invention of paper in China Paper-folding begins shortly after in China, Korea, Japan 800s: Japanese develop basic models for ceremonial folding 1200s: Origami globalized throughout Japan 1682: Earliest book to describe origami 1797: How to fold 1,000 cranes published 1954: Yoshizawa’s book formalizes a notational system 1940s-1960s: Origami popularized in the U.S. and throughout the world History of Origami Mathematics 1893: Geometric exercises in paper folding by Row 1936: Origami first analyzed according to axioms by Beloch 1989-present: Huzita-Hatori axioms Flat-folding theorems: Maekawa, Kawasaki, Justin, Hull TreeMaker designed by Lang Origami sekkei – “technical origami” Rigid origami Applications from the large to very small Miura-Ori Japanese solar sail “Eyeglass” space telescope Lawrence Livermore National Laboratory Science of the small Heart stents Titanium hydride printing DNA origami Protein-folding Two broad categories Foldability (discrete, computational complexity) Given a pattern of creases, when does the folded model lie flat? Design (geometry, optimization) How much detail can added to an origami model, and how efficiently can this be done? Flat-Foldability of Crease Patterns 훗 Three criteria for 훗: Continuity, Piecewise isometry, Noncrossing 2-Colorable Under the mapping 훗, some faces are flipped while others are only translated and rotated. Maekawa-Justin Theorem At any interior vertex, the number of mountain and valley folds differ by two. -
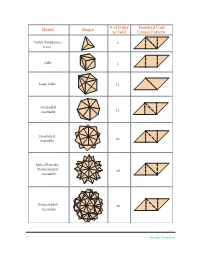
Sonobe Assembly Guide for a Few Polyhedra
Model Shape # of Units Finished Unit to Fold Crease Pattern Toshie Takahama’s 3 Jewel Cube 6 Large Cube 12 Octahedral Assembly 12 Icosahedral Assembly 30 Spiked Pentakis Dodecahedral 60 Assembly Dodecahedral 90 Assembly 2 Sonobe Variations Sonobe Assembly Basics Sonobe assemblies are essentially “pyramidized” constructing a polyhedron, the key thing to re- polyhedra, each pyramid consisting of three So- member is that the diagonal ab of each Sonobe nobe units. The figure below shows a generic So- unit will lie along an edge of the polyhedron. nobe unit and how to form one pyramid. When a Pocket Tab Forming one Tab pyramid Pocket b A generic Sonobe unit representation Sonobe Assembly Guide for a Few Polyhedra 1. Toshie’s Jewel: Crease three finished units as tabs and pockets. This assembly is also sometimes explained in the table on page 2. Form a pyramid known as a Crane Egg. as above. Then turn the assembly upside down 2. Cube Assembly: Crease six finished units as and make another pyramid with the three loose explained in the table on page 2. Each face will be made up of 3 the center square of one unit and the tabs of two other units. 4 Do Steps 1 and 2 to form one face. Do Steps 3 and 4 to form one corner or vertex. Continue 1 2 interlocking in this manner to arrive at the finished cube. Sonobe Variations 3 3. Large Cube Assembly: Crease 12 finished units as explained on page 2. 5 6 3 The 12-unit large cube is the only assembly that does not involve pyramidizing. -

Folding a Paper Strip to Minimize Thickness✩
Folding a Paper Strip to Minimize Thickness✩ Erik D. Demainea, David Eppsteinb, Adam Hesterbergc, Hiro Itod, Anna Lubiwe, Ryuhei Ueharaf, Yushi Unog aComputer Science and Artificial Intelligence Lab, Massachusetts Institute of Technology, Cambridge, USA bComputer Science Department, University of California, Irvine, USA cDepartment of Mathematics, Massachusetts Institute of Technology, USA dSchool of Informatics and Engineering, University of Electro-Communications, Tokyo, Japan eDavid R. Cheriton School of Computer Science, University of Waterloo, Ontario, Canada fSchool of Information Science, Japan Advanced Institute of Science and Technology, Ishikawa, Japan gGraduate School of Science, Osaka Prefecture University, Osaka, Japan Abstract In this paper, we study how to fold a specified origami crease pattern in order to minimize the impact of paper thickness. Specifically, origami designs are often expressed by a mountain-valley pattern (plane graph of creases with relative fold orientations), but in general this specification is consistent with exponentially many possible folded states. We analyze the complexity of finding the best consistent folded state according to two metrics: minimizing the total number of layers in the folded state (so that a “flat folding” is indeed close to flat), and minimizing the total amount of paper required to execute the folding (where “thicker” creases consume more paper). We prove both problems strongly NP- complete even for 1D folding. On the other hand, we prove both problems fixed-parameter tractable in 1D with respect to the number of layers. Keywords: linkage, NP-complete, optimization problem, rigid origami. 1. Introduction Most results in computational origami design assume an idealized, zero- thickness piece of paper. This approach has been highly successful, revolution- izing artistic origami over the past few decades. -

A Survey of Folding and Unfolding in Computational Geometry
Combinatorial and Computational Geometry MSRI Publications Volume 52, 2005 A Survey of Folding and Unfolding in Computational Geometry ERIK D. DEMAINE AND JOSEPH O’ROURKE Abstract. We survey results in a recent branch of computational geome- try: folding and unfolding of linkages, paper, and polyhedra. Contents 1. Introduction 168 2. Linkages 168 2.1. Definitions and fundamental questions 168 2.2. Fundamental questions in 2D 171 2.3. Fundamental questions in 3D 175 2.4. Fundamental questions in 4D and higher dimensions 181 2.5. Protein folding 181 3. Paper 183 3.1. Categorization 184 3.2. Origami design 185 3.3. Origami foldability 189 3.4. Flattening polyhedra 191 4. Polyhedra 193 4.1. Unfolding polyhedra 193 4.2. Folding polygons into convex polyhedra 196 4.3. Folding nets into nonconvex polyhedra 199 4.4. Continuously folding polyhedra 200 5. Conclusion and Higher Dimensions 201 Acknowledgements 202 References 202 Demaine was supported by NSF CAREER award CCF-0347776. O’Rourke was supported by NSF Distinguished Teaching Scholars award DUE-0123154. 167 168 ERIKD.DEMAINEANDJOSEPHO’ROURKE 1. Introduction Folding and unfolding problems have been implicit since Albrecht D¨urer [1525], but have not been studied extensively in the mathematical literature until re- cently. Over the past few years, there has been a surge of interest in these problems in discrete and computational geometry. This paper gives a brief sur- vey of most of the work in this area. Related, shorter surveys are [Connelly and Demaine 2004; Demaine 2001; Demaine and Demaine 2002; O’Rourke 2000]. We are currently preparing a monograph on the topic [Demaine and O’Rourke ≥ 2005]. -

Generating Folding Sequences from Crease Patterns of Flat-Foldable Origami
Generating Folding Sequences from Crease Patterns of Flat-Foldable Origami Hugo A. Akitaya∗ Jun Mitaniy Yoshihiro Kanamoriy Yukio Fukuiy University of Tsukuba University of Tsukuba / JST ERATO University of Tsukuba University of Tsukuba (b) (a) Figure 1: (a) Example of a step sequence graph containing several possible ways of simplifying the input crease pattern. (b) Results obtained using the path highlighted in orange from Figure 1(a). to fold the paper into the origami design, since crease patterns show only where each crease must be made and not folding instructions. In fact, folding an origami model by its crease pattern may be a difficult task even for people experienced in origami [Lang 2012]. According to Lang, a linear sequence of small steps, such as usually (a) (b) portrayed in traditional diagrams, might not even exist and all the folds would have to be executed simultaneously. Figure 2: (a) Crease pattern and (b) folded form of the “Penguin”. We introduce a system capable of identifying if a folding sequence Design by Hideo Komatsu. Images redrawn by authors. exists using a predetermined set of folds by modeling the origami steps as graph rewriting steps. It also creates origami diagrams semi-automatically from the input of a crease pattern of a flat 1 Problem and Motivation origami. Our system provides the automatic addition of traditional symbols used in origami diagrams and 3D animations in order to The most common form to convey origami is through origami di- help people who are inexperienced in folding crease patterns as agrams, which are step-by-step sequences as shown in Figure 1b. -
![Arxiv:2105.14305V1 [Cs.CG] 29 May 2021](https://docslib.b-cdn.net/cover/2277/arxiv-2105-14305v1-cs-cg-29-may-2021-1052277.webp)
Arxiv:2105.14305V1 [Cs.CG] 29 May 2021
Efficient Folding Algorithms for Regular Polyhedra ∗ Tonan Kamata1 Akira Kadoguchi2 Takashi Horiyama3 Ryuhei Uehara1 1 School of Information Science, Japan Advanced Institute of Science and Technology (JAIST), Ishikawa, Japan fkamata,[email protected] 2 Intelligent Vision & Image Systems (IVIS), Tokyo, Japan [email protected] 3 Faculty of Information Science and Technology, Hokkaido University, Hokkaido, Japan [email protected] Abstract We investigate the folding problem that asks if a polygon P can be folded to a polyhedron Q for given P and Q. Recently, an efficient algorithm for this problem has been developed when Q is a box. We extend this idea to regular polyhedra, also known as Platonic solids. The basic idea of our algorithms is common, which is called stamping. However, the computational complexities of them are different depending on their geometric properties. We developed four algorithms for the problem as follows. (1) An algorithm for a regular tetrahedron, which can be extended to a tetramonohedron. (2) An algorithm for a regular hexahedron (or a cube), which is much efficient than the previously known one. (3) An algorithm for a general deltahedron, which contains the cases that Q is a regular octahedron or a regular icosahedron. (4) An algorithm for a regular dodecahedron. Combining these algorithms, we can conclude that the folding problem can be solved pseudo-polynomial time when Q is a regular polyhedron and other related solid. Keywords: Computational origami folding problem pseudo-polynomial time algorithm regular poly- hedron (Platonic solids) stamping 1 Introduction In 1525, the German painter Albrecht D¨urerpublished his masterwork on geometry [5], whose title translates as \On Teaching Measurement with a Compass and Straightedge for lines, planes, and whole bodies." In the book, he presented each polyhedron by drawing a net, which is an unfolding of the surface of the polyhedron to a planar layout without overlapping by cutting along its edges. -

GEOMETRIC FOLDING ALGORITHMS I
P1: FYX/FYX P2: FYX 0521857570pre CUNY758/Demaine 0 521 81095 7 February 25, 2007 7:5 GEOMETRIC FOLDING ALGORITHMS Folding and unfolding problems have been implicit since Albrecht Dürer in the early 1500s but have only recently been studied in the mathemat- ical literature. Over the past decade, there has been a surge of interest in these problems, with applications ranging from robotics to protein folding. With an emphasis on algorithmic or computational aspects, this comprehensive treatment of the geometry of folding and unfolding presents hundreds of results and more than 60 unsolved “open prob- lems” to spur further research. The authors cover one-dimensional (1D) objects (linkages), 2D objects (paper), and 3D objects (polyhedra). Among the results in Part I is that there is a planar linkage that can trace out any algebraic curve, even “sign your name.” Part II features the “fold-and-cut” algorithm, establishing that any straight-line drawing on paper can be folded so that the com- plete drawing can be cut out with one straight scissors cut. In Part III, readers will see that the “Latin cross” unfolding of a cube can be refolded to 23 different convex polyhedra. Aimed primarily at advanced undergraduate and graduate students in mathematics or computer science, this lavishly illustrated book will fascinate a broad audience, from high school students to researchers. Erik D. Demaine is the Esther and Harold E. Edgerton Professor of Elec- trical Engineering and Computer Science at the Massachusetts Institute of Technology, where he joined the faculty in 2001. He is the recipient of several awards, including a MacArthur Fellowship, a Sloan Fellowship, the Harold E. -

Universal Folding Pathways of Polyhedron Nets
Universal folding pathways of polyhedron nets Paul M. Dodda, Pablo F. Damascenob, and Sharon C. Glotzera,b,c,d,1 aChemical Engineering Department, University of Michigan, Ann Arbor, MI 48109; bApplied Physics Program, University of Michigan, Ann Arbor, MI 48109; cDepartment of Materials Science and Engineering, University of Michigan, Ann Arbor, MI 48109; and dBiointerfaces Institute, University of Michigan, Ann Arbor, MI 48109 Contributed by Sharon C. Glotzer, June 6, 2018 (sent for review January 17, 2018; reviewed by Nuno Araujo and Andrew L. Ferguson) Low-dimensional objects such as molecular strands, ladders, and navigate, thermodynamically, from a denatured (unfolded) state sheets have intrinsic features that affect their propensity to fold to a natured (folded) one. Even after many decades of study, into 3D objects. Understanding this relationship remains a chal- however, a universal relationship between molecular sequence lenge for de novo design of functional structures. Using molecular and folded state—which could provide crucial insight into the dynamics simulations, we investigate the refolding of the 24 causes and potential treatments of many diseases—remains out possible 2D unfoldings (“nets”) of the three simplest Platonic of reach (11–13). shapes and demonstrate that attributes of a net’s topology— In this work, we study the thermodynamic foldability of 2D net compactness and leaves on the cutting graph—correlate nets for all five Platonic solids. Despite being the simplest and with thermodynamic folding propensity. To -

Industrial Product Design by Using Two-Dimensional Material in the Context of Origamic Structure and Integrity
Industrial Product Design by Using Two-Dimensional Material in the Context of Origamic Structure and Integrity By Nergiz YİĞİT A Dissertation Submitted to the Graduate School in Partial Fulfillment of the Requirements for the Degree of MASTER OF INDUSTRIAL DESIGN Department: Industrial Design Major: Industrial Design İzmir Institute of Technology İzmir, Turkey July, 2004 We approve the thesis of Nergiz YİĞİT Date of Signature .................................................. 28.07.2004 Assist. Prof. Yavuz SEÇKİN Supervisor Department of Industrial Design .................................................. 28.07.2004 Assist.Prof. Dr. Önder ERKARSLAN Department of Industrial Design .................................................. 28.07.2004 Assist. Prof. Dr. A. Can ÖZCAN İzmir University of Economics, Department of Industrial Design .................................................. 28.07.2004 Assist. Prof. Yavuz SEÇKİN Head of Department ACKNOWLEDGEMENTS I would like to thank my advisor Assist. Prof. Yavuz Seçkin for his continual advice, supervision and understanding in the research and writing of this thesis. I would also like to thank Assist. Prof. Dr. A. Can Özcan, and Assist.Prof. Dr. Önder Erkarslan for their advices and supports throughout my master’s studies. I am grateful to my friends Aslı Çetin and Deniz Deniz for their invaluable friendships, and I would like to thank to Yankı Göktepe for his being. I would also like to thank my family for their patience, encouragement, care, and endless support during my whole life. ABSTRACT Throughout the history of industrial product design, there have always been attempts to shape everyday objects from a single piece of semi-finished industrial materials such as plywood, sheet metal, plastic sheet and paper-based sheet. One of the ways to form these two-dimensional materials into three-dimensional products is bending following cutting. -

Planning to Fold Multiple Objects from a Single Self-Folding Sheet
Planning to Fold Multiple Objects from a Single Self-Folding Sheet Byoungkwon An∗ Nadia Benbernou∗ Erik D. Demaine∗ Daniela Rus∗ Abstract This paper considers planning and control algorithms that enable a programmable sheet to realize different shapes by autonomous folding. Prior work on self-reconfiguring machines has considered modular systems in which independent units coordinate with their neighbors to realize a desired shape. A key limitation in these prior systems is the typically many operations to make and break connections with neighbors, which lead to brittle performance. We seek to mitigate these difficulties through the unique concept of self-folding origami with a universal fixed set of hinges. This approach exploits a single sheet composed of interconnected triangular sections. The sheet is able to fold into a set of predetermined shapes using embedded actuation. We describe the planning algorithms underlying these self-folding sheets, forming a new family of reconfigurable robots that fold themselves into origami by actuating edges to fold by desired angles at desired times. Given a flat sheet, the set of hinges, and a desired folded state for the sheet, the algorithms (1) plan a continuous folding motion into the desired state, (2) discretize this motion into a practicable sequence of phases, (3) overlay these patterns and factor the steps into a minimum set of groups, and (4) automatically plan the location of actuators and threads on the sheet for implementing the shape-formation control. 1 Introduction Over the past two decades we have seen great progress toward creating self-assembling, self-reconfiguring, self-replicating, and self-organizing machines [YSS+06]. -

Origamizing Polyhedral Surfaces Tomohiro Tachi
1 Origamizing Polyhedral Surfaces Tomohiro Tachi Abstract—This paper presents the first practical method for “origamizing” or obtaining the folding pattern that folds a single sheet of material into a given polyhedral surface without any cut. The basic idea is to tuck fold a planar paper to form a three-dimensional shape. The main contribution is to solve the inverse problem; the input is an arbitrary polyhedral surface and the output is the folding pattern. Our approach is to convert this problem into a problem of laying out the polygons of the surface on a planar paper by introducing the concept of tucking molecules. We investigate the equality and inequality conditions required for constructing a valid crease pattern. We propose an algorithm based on two-step mapping and edge splitting to solve these conditions. The two-step mapping precalculates linear equalities and separates them from other conditions. This allows an interactive manipulation of the crease pattern in the system implementation. We present the first system for designing three-dimensional origami, enabling a user can interactively design complex spatial origami models that have not been realizable thus far. Index Terms—Origami, origami design, developable surface, folding, computer-aided design. ✦ 1 INTRODUCTION proposed to obtain nearly developable patches represented as RIGAMI is an art of folding a single piece of paper triangle meshes, either by segmenting the surface through O into a variety of shapes without cutting or stretching the fitting of the patches to cones, as proposed by Julius it. Creating an origami with desired properties, particularly a [4], or by minimizing the Gauss area, as studied by Wang desired shape, is known as origami design. -

Practical Applications of Rigid Thick Origami in Kinetic Architecture
PRACTICAL APPLICATIONS OF RIGID THICK ORIGAMI IN KINETIC ARCHITECTURE A DARCH PROJECT SUBMITTED TO THE GRADUATE DIVISION OF THE UNIVERSITY OF HAWAI‘I AT MĀNOA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTORATE OF ARCHITECTURE DECEMBER 2015 By Scott Macri Dissertation Committee: David Rockwood, Chairperson David Masunaga Scott Miller Keywords: Kinetic Architecture, Origami, Rigid Thick Acknowledgments I would like to gratefully acknowledge and give a huge thanks to all those who have supported me. To the faculty and staff of the School of Architecture at UH Manoa, who taught me so much, and guided me through the D.Arch program. To Kris Palagi, who helped me start this long dissertation journey. To David Rockwood, who had quickly learned this material and helped me finish and produced a completed document. To my committee members, David Masunaga, and Scott Miller, who have stayed with me from the beginning and also looked after this document with a sharp eye and critical scrutiny. To my wife, Tanya Macri, and my parents, Paul and Donna Macri, who supported me throughout this dissertation and the D.Arch program. Especially to my father, who introduced me to origami over two decades ago, without which, not only would this dissertation not have been possible, but I would also be with my lifelong hobby and passion. And finally, to Paul Sheffield, my continual mentor in not only the study and business of architecture, but also mentored me in life, work, my Christian faith, and who taught me, most importantly, that when life gets stressful, find a reason to laugh about it.