DOCSLIB.ORG

A Study of the Reactions, Beryllium-9(Helium-3,Neutron

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Study of the Reactions, Beryllium-9(Helium-3,Neutron Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1962 A Study of the Reactions, Beryllium-9(helium-3,neutron)carbon-11, Lithium-7(helium-3,neutron)boron-9 and Carbon-13(helium-3,neutron)oxygen-15 by Time- Of-Flight Techniques. Jerome Lewis Duggan Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Duggan, Jerome Lewis, "A Study of the Reactions, Beryllium-9(helium-3,neutron)carbon-11, Lithium-7(helium-3,neutron)boron-9 and Carbon-13(helium-3,neutron)oxygen-15 by Time-Of-Flight Techniques." (1962). LSU Historical Dissertations and Theses. 718. https://digitalcommons.lsu.edu/gradschool_disstheses/718 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. This dissertation has been 62—3644 microfilmed exactly as received DUGGAN, Jerome Lewis, 1933- A STUDY OF THE REACTIONS, Be9(He3,n)Cn , Li7(He3,n)B9 AND C13(He3,n)Ol5 , BY TIME-OF- FUGHT TECHNIQUES. Louisiana State University, Ph.D., 1962 Physics, nuclear University Microfilms, Inc., Ann Arbor, Michigan A STUDY OF THE REACTIONS, Be9(He3 ,n)C1;L, L i7(He3,n)B AND C13(He3 ,n )0 15, BY TIME-OF-FLIGHT TECHNIQUES A D issertation Submitted to the Graduate Faculty of the Louisiana State University and A gricultural and Mechanical College in partial fulfillm ent of the requirements for the degree of Doctor of Philosophy i n The Department of Physics by Jerome Lewis Duggan B. A., North Texas State College, 1955 M. A., North Texas State College, 1956 January, 1962 ACKNOWLEDGMENT The author wishes to express his appreciation and gratitude to his research advisors, Dr. P. D. M iller and Dr. W. M. Good of the Oak Ridge National Laboratory and Dr. V. E. Parker of Louisiana State University, for their assistance and encouragement during the course of this work. In addition he wishes to thank Dr. R. F. Gabbard of the University of Kentucky, Dr. J. H. Neiler, Dr. G. R. Satchler, Mr. R. P. Cumby and Mr. M. C. Taylor of the Oak Ridge National Laboratory for their assistance in this project. Also, appreciation is due Mrs. B. A. Denning for typing the manuscript of this thesis. Finally, he would like to recognize the financial support of the Graduate Fellowship Program of the Oak Ridge Institute of Nuclear Studies and the Physics Division of the Oak Ridge National Laboratory. TABLE OF CONTENTS PAGE ACKNOWLEDGMENT................................................................................................................. i i LIST OF TABLES................................................................................................................. v LIST OF FIGURES ............................................................................................................ v i ABSTRACT................................................................................................................................ x l CHAPTERS I. INTRODUCTION......................................................................................................... 1 The Importance of He R eactions ................................................. 1 Reaction M echanisms ............................................................................... 3 The Levels in $ } , an d C ^ ...................................................... 9 I I . EXPERIMENTAL APPARATUS AND PROCEDURE.............................................. 15 Spectrometer Resolving Power ........................................................... 15 Sources of Energy Spread ............................. 18 Elapsed Time M easurement ..................................................................... 21 Refinements for (He ,n) R eactions ............................................ 23 Electronics .................................................................................................. 33 I I I . PRESENTATION OF DATA.................................................................................... 44 Plastic Scintillator Efficiency ................................................. 44 Pulse S pectra ............................................................................................. 48 The Be^(He^Jn)C11 R eaction ................................................................ 51 The C13(He3,n)015 Reaction ................................................................ 53 The Li^(He3,n)B^ R eactio n ........................ 65 CHAPTERS - ■ PAGE Measured Q V alu es ................................................................................... 72 Discussion of Errors ............................................................................... j6 IV . CALCULATIONS AND RESULTS.......................................................................... 80 Plane Wave C alculations ............................. 80 Distorted Wave C alcu latio n s .............................................................. 90 Discussion of Theoretical Calculations and Results . 95 BIBLIOGRAPHY..................................................................................................................... I l 6 APPENDIX..................................................................................................................................... 121 V LIST OF TABLES TABLE PAGE I. Measured Q, V alues ............................................................................................... 77 II. Spin and Parity Assignments ...................................................................... 96 III. Optical Model Param eters ........................................................................... 97 LIST OF FIGURES FIGURE PAGE 1. Reciprocal Velocities for Neutron Groups from Be'^(He3 ,n )C '^ ‘ ...................................................................................................20 2. Block Diagram of Post Acceleration Pulsing S ystem ......................... 25 3. Average Target Current vs Reciprocal Pulser V oltage............................. 26 M easured 7 -Ray Duration vs Pulser V oltage ..............................................27 5 . Electronics Used to Study Time Resolution P a r a m e t e r s ...................................................................................................................... 3° 6 . Time Converter ...................................................................................... 3k 7 . Block Diagram for Time-of-Flight Spectrum............................................. 35 8 . Time-of-Flight Spectrum for Neutrons from C1 3 (He3 ,n ) 0 15 at 0 ^ = 0°, E ^ ~ 2 Mev and Flight Path 3 m...........................* ................................................................37 9. Time Spectrum for In7(He 3 ,n )B ? a t ER 3 = 2 .3 5 Mev, 0=0° and Flight P a th 6 m. j f ............................................................................................................ 38 10. Time Spectrum for Be^(He3,n)C'*"*' a t Eg e 3 = 2 .5 Mev, 0 = 0° and Flight Path 6 m..................................................................................39 11. Block Diagram for Pulse Spectrum ................................................................l)-0 12. Pulse Height Spectrum for 9*83 Mev Neutrons from Be^(He3,n )C '1''*' ^1 13. Block Diagram for Pulse Spectrum with Memory S p litte r ........................................................................................................k2 v i i FIGURE PAGE 14. Calculated Efficiency of ^ x 3 in. Plastic Scintillator ........................................................................................................ 47 1 5 . Theoretical Pulse Spectra of 10-Mev Neutrons for 4 x 3 in. Plastic S cin tillato r .................................................. 5 ° 1 6 . Absolute Efficiency of 3 x 4-in. Plastic Scintillator with Bias Level at 1.1 Mev ........................................... 52 1 7 . Angular Distribution for Ground State Neutrons from Be^(He'^,n)C 11 a t ERe3 = 2 .1 Mev .................................................. 5^ 18s. Angular D istribution of 1st Excited State Neutrons from Be (He ,n)C at EHe3 = 2 .1 Mev ........................................................................................................ 55 1 9 . Angular Distribution for 2nd Excited State Neutrons from Be^(He^,n)C‘^ ‘ at EHe3 = 2 .1 Mev ........................................................................................ 56 20. Angular Distribution of 3rd Excited state Neutrons from Be^He^nJC 11 a t EHe3 = 2 .1 Mev ........................................................................................................ 57 21. Angular Distribution of 4th Excited State Neutrons from Be^(He^,n)C^ at ERe3 = 2 .1 Mev ......................................................................................................... ~ 58 22. Excitation Function for Be^(He^,n)C'^‘, Ground State Neutrons ............................................................................... 59 2 3 . Excitation Function for Be^(He^,n)C^, 1st Excited State ......................................................................................... 60 FIGURE 9 3 11 2b. Excitation Function for Be (He ,n)C , 2nd Excited State .................................. ............................ 2 5 . Excitation Function of the 3rd Excited S tate
Load more

Recommended publications
  • An Alternate Graphical Representation of Periodic Table of Chemical Elements Mohd Abubakr1, Microsoft India (R&D) Pvt
    An Alternate Graphical Representation of Periodic table of Chemical Elements Mohd Abubakr1, Microsoft India (R&D) Pvt. Ltd, Hyderabad, India. [email protected] Abstract Periodic table of chemical elements symbolizes an elegant graphical representation of symmetry at atomic level and provides an overview on arrangement of electrons. It started merely as tabular representation of chemical elements, later got strengthened with quantum mechanical description of atomic structure and recent studies have revealed that periodic table can be formulated using SO(4,2) SU(2) group. IUPAC, the governing body in Chemistry, doesn‟t approve any periodic table as a standard periodic table. The only specific recommendation provided by IUPAC is that the periodic table should follow the 1 to 18 group numbering. In this technical paper, we describe a new graphical representation of periodic table, referred as „Circular form of Periodic table‟. The advantages of circular form of periodic table over other representations are discussed along with a brief discussion on history of periodic tables. 1. Introduction The profoundness of inherent symmetry in nature can be seen at different depths of atomic scales. Periodic table symbolizes one such elegant symmetry existing within the atomic structure of chemical elements. This so called „symmetry‟ within the atomic structures has been widely studied from different prospects and over the last hundreds years more than 700 different graphical representations of Periodic tables have emerged [1]. Each graphical representation of chemical elements attempted to portray certain symmetries in form of columns, rows, spirals, dimensions etc. Out of all the graphical representations, the rectangular form of periodic table (also referred as Long form of periodic table or Modern periodic table) has gained wide acceptance.
    [Show full text]
  • The Development of the Periodic Table and Its Consequences Citation: J
    Firenze University Press www.fupress.com/substantia The Development of the Periodic Table and its Consequences Citation: J. Emsley (2019) The Devel- opment of the Periodic Table and its Consequences. Substantia 3(2) Suppl. 5: 15-27. doi: 10.13128/Substantia-297 John Emsley Copyright: © 2019 J. Emsley. This is Alameda Lodge, 23a Alameda Road, Ampthill, MK45 2LA, UK an open access, peer-reviewed article E-mail: [email protected] published by Firenze University Press (http://www.fupress.com/substantia) and distributed under the terms of the Abstract. Chemistry is fortunate among the sciences in having an icon that is instant- Creative Commons Attribution License, ly recognisable around the world: the periodic table. The United Nations has deemed which permits unrestricted use, distri- 2019 to be the International Year of the Periodic Table, in commemoration of the 150th bution, and reproduction in any medi- anniversary of the first paper in which it appeared. That had been written by a Russian um, provided the original author and chemist, Dmitri Mendeleev, and was published in May 1869. Since then, there have source are credited. been many versions of the table, but one format has come to be the most widely used Data Availability Statement: All rel- and is to be seen everywhere. The route to this preferred form of the table makes an evant data are within the paper and its interesting story. Supporting Information files. Keywords. Periodic table, Mendeleev, Newlands, Deming, Seaborg. Competing Interests: The Author(s) declare(s) no conflict of interest. INTRODUCTION There are hundreds of periodic tables but the one that is widely repro- duced has the approval of the International Union of Pure and Applied Chemistry (IUPAC) and is shown in Fig.1.
    [Show full text]
  • Helium Adsorption on Lithium Substrates
    JLowTempPhys DOI 10.1007/s10909-007-9516-5 Helium Adsorption on Lithium Substrates E. Van Cleve · P. Taborek · J.E. Rutledge Received: 25 July 2007 / Accepted: 13 September 2007 © Springer Science+Business Media 2007 Abstract We have developed a cryogenic pulsed laser deposition (PLD) system to deposit lithium films onto a quartz crystal microbalance (QCM) at 4 K. Adsorption isotherms of 4He on lithium were measured in the temperature range between 1.42 K and 2.5 K. The isotherms are qualitatively different from isotherms on strong sub- strates such as gold and weak substrates such as cesium. There is no evidence of the formation of solid-like layers of helium, and the helium coverage is approximately linear in the pressure over a wide range. By measuring the low coverage slope of the isotherms, the binding energy of helium to lithium was found to be approxi- mately −13.6 K. For lithium substrates less than approximately 100 layers thick, the chemical potential at which the superfluid transition was observed was surprisingly sensitive to the details of lithium deposition. Keywords Helium films · Pulsed laser deposition · Superfluidity · Alkali metal 1 Introduction When helium is adsorbed onto a strong heterogenous substrate such as gold, the first 2 or 3 statistical layers are solid-like. The nature of these layers is not yet clear, but the layers are amorphous and do not participate significantly in superflow at high coverages. Superfluidity on strong substrates requires a minimum critical coverage to saturate the solid-like layers, and the superfluid phase which forms at higher cover- ages flows over these layers and does not interact directly with the strong, short range This work was supported by NSF grant DMR 0509685.
    [Show full text]
  • Of the Periodic Table
    of the Periodic Table teacher notes Give your students a visual introduction to the families of the periodic table! This product includes eight mini- posters, one for each of the element families on the main group of the periodic table: Alkali Metals, Alkaline Earth Metals, Boron/Aluminum Group (Icosagens), Carbon Group (Crystallogens), Nitrogen Group (Pnictogens), Oxygen Group (Chalcogens), Halogens, and Noble Gases. The mini-posters give overview information about the family as well as a visual of where on the periodic table the family is located and a diagram of an atom of that family highlighting the number of valence electrons. Also included is the student packet, which is broken into the eight families and asks for specific information that students will find on the mini-posters. The students are also directed to color each family with a specific color on the blank graphic organizer at the end of their packet and they go to the fantastic interactive table at www.periodictable.com to learn even more about the elements in each family. Furthermore, there is a section for students to conduct their own research on the element of hydrogen, which does not belong to a family. When I use this activity, I print two of each mini-poster in color (pages 8 through 15 of this file), laminate them, and lay them on a big table. I have students work in partners to read about each family, one at a time, and complete that section of the student packet (pages 16 through 21 of this file). When they finish, they bring the mini-poster back to the table for another group to use.
    [Show full text]
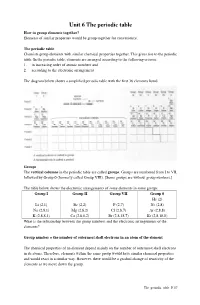
  • Unit 6 the Periodic Table How to Group Elements Together? Elements of Similar Properties Would Be Group Together for Convenience
    Unit 6 The periodic table How to group elements together? Elements of similar properties would be group together for convenience. The periodic table Chemists group elements with similar chemical properties together. This gives rise to the periodic table. In the periodic table, elements are arranged according to the following criteria: 1. in increasing order of atomic numbers and 2. according to the electronic arrangement The diagram below shows a simplified periodic table with the first 36 elements listed. Groups The vertical columns in the periodic table are called groups . Groups are numbered from I to VII, followed by Group 0 (formerly called Group VIII). [Some groups are without group numbers.] The table below shows the electronic arrangements of some elements in some groups. Group I Group II Group VII Group 0 He (2) Li (2,1) Be (2,2) F (2,7) Ne (2,8) Na (2,8,1) Mg (2,8,2) Cl (2,8,7) Ar (2,8,8) K (2,8,8,1) Ca (2,8,8,2) Br (2,8,18,7) Kr (2,8,18,8) What is the relationship between the group numbers and the electronic arrangements of the elements? Group number = the number of outermost shell electrons in an atom of the element The chemical properties of an element depend mainly on the number of outermost shell electrons in its atoms. Therefore, elements within the same group would have similar chemical properties and would react in a similar way. However, there would be a gradual change of reactivity of the elements as we move down the group.
    [Show full text]
  • Periodic Table 1 Periodic Table
    Periodic table 1 Periodic table This article is about the table used in chemistry. For other uses, see Periodic table (disambiguation). The periodic table is a tabular arrangement of the chemical elements, organized on the basis of their atomic numbers (numbers of protons in the nucleus), electron configurations , and recurring chemical properties. Elements are presented in order of increasing atomic number, which is typically listed with the chemical symbol in each box. The standard form of the table consists of a grid of elements laid out in 18 columns and 7 Standard 18-column form of the periodic table. For the color legend, see section Layout, rows, with a double row of elements under the larger table. below that. The table can also be deconstructed into four rectangular blocks: the s-block to the left, the p-block to the right, the d-block in the middle, and the f-block below that. The rows of the table are called periods; the columns are called groups, with some of these having names such as halogens or noble gases. Since, by definition, a periodic table incorporates recurring trends, any such table can be used to derive relationships between the properties of the elements and predict the properties of new, yet to be discovered or synthesized, elements. As a result, a periodic table—whether in the standard form or some other variant—provides a useful framework for analyzing chemical behavior, and such tables are widely used in chemistry and other sciences. Although precursors exist, Dmitri Mendeleev is generally credited with the publication, in 1869, of the first widely recognized periodic table.
    [Show full text]
  • The Noble Gases
    INTERCHAPTER K The Noble Gases When an electric discharge is passed through a noble gas, light is emitted as electronically excited noble-gas atoms decay to lower energy levels. The tubes contain helium, neon, argon, krypton, and xenon. University Science Books, ©2011. All rights reserved. www.uscibooks.com Title General Chemistry - 4th ed Author McQuarrie/Gallogy Artist George Kelvin Figure # fig. K2 (965) Date 09/02/09 Check if revision Approved K. THE NOBLE GASES K1 2 0 Nitrogen and He Air P Mg(ClO ) NaOH 4 4 2 noble gases 4.002602 1s2 O removal H O removal CO removal 10 0 2 2 2 Ne Figure K.1 A schematic illustration of the removal of O2(g), H2O(g), and CO2(g) from air. First the oxygen is removed by allowing the air to pass over phosphorus, P (s) + 5 O (g) → P O (s). 20.1797 4 2 4 10 2s22p6 The residual air is passed through anhydrous magnesium perchlorate to remove the water vapor, Mg(ClO ) (s) + 6 H O(g) → Mg(ClO ) ∙6 H O(s), and then through sodium hydroxide to remove 18 0 4 2 2 4 2 2 the carbon dioxide, NaOH(s) + CO2(g) → NaHCO3(s). The gas that remains is primarily nitrogen Ar with about 1% noble gases. 39.948 3s23p6 36 0 The Group 18 elements—helium, K-1. The Noble Gases Were Kr neon, argon, krypton, xenon, and Not Discovered until 1893 83.798 radon—are called the noble gases 2 6 4s 4p and are noteworthy for their rela- In 1893, the English physicist Lord Rayleigh noticed 54 0 tive lack of chemical reactivity.
    [Show full text]
  • Vapour-Liquid Equilibria of the Neon-Helium System, Cryogenics, 7, 177 (1967) Easitrain – European Advanced Superconductivity Innovation and Training
    Fluid properties modeling Jakub Tkaczuk 1,*, Eric Lemmon 2, Ian Bell 2, Francois Millet 1, Nicolas Luchier 1 1 Université Grenoble Alpes, CEA IRIG-dSBT, F-38000 Grenoble, France 2 National Institute of Standards and Technology, Boulder, Colorado 80305, United States * [email protected] Abstract Phase envelope Based upon the conceptual design reports for the FCC cryogenic With the available data points, a shape of the vapor-liquid equilibrium system, the need for more accurate thermodynamic property models of and the occurrence of liquid-liquid equilibrium can be defined (most mixtures was identified. Both academic institutes and world-wide probably no LLE for helium-neon). industries have identified the lack of reliable equation of state for mixtures used at very low temperatures. Detailed cryogenic architecture modeling and design cannot be assessed without valid fluid properties. Therefore, the latter is the focus of this work. Initially driven by the FCC study, the modeling was extended to other fluids beneficial for scientific and industrial application beyond the FCC needs. The properties are modeled for the mixtures of some noble gases with the use of multi-fluid Helmholtz-energy-explicit models: helium-neon, neon-argon, and helium-argon. The on-going studies are performed at CEA-Grenoble, France and at the National Institute of Standards and Technology, U.S. Helmholtz energy equation of state The Helmholtz free energy 훼(훿, 휏) is a thermodynamic potential, which measures useful work obtainable from a closed system. Defining the equation of state (EoS) as a Helmholtz energy-explicit function can be particularly advantageous. Fig. 2.
    [Show full text]
  • Mass Spectrometric Measurement of Helium Isotopes and Tritium in Water Samples
    Mass spectrometric measurement of helium isotopes and tritium in water samples Andrea Ludin1, Ralf Weppernig1, Gerhard Bönisch1, and Peter Schlosser1,2 1Lamont-Doherty Earth Observatory of Columbia University Route 9W Palisades, NY 10964 2Department of Earth and Environmental Sciences Columbia University New York, NY 10027 downloaded from: http://www.ldeo.columbia.edu/~etg/ms_ms/Ludin_et_al_MS_Paper.html 1 ABSTRACT The design, setup and routine performance of systems for mass spectrometric measurement of helium isotopes and tritium of water samples by the 3He ingrowth method are described using two systems operated in the noble gas laboratory of the Lamont-Doherty Earth Observatory as examples. The systems are built around commercially available mass spectrometers and are equipped with specially designed sample inlet and purification systems including a series of cryogenically cooled traps for removal of water and permanent gases, as well as for separation of helium from neon. Neon isotopes are measured simultaneously to the helium isotope measurements in quadrupole mass spectrometers. The systems are fully automated for high sample throughput and high precision. Typical precisions for measurement of tritium, δ 3He, and the 4He and neon concentrations are ± 1 to ± 2 %, ± 0.15 to ± 0.2 %, and ± 0.2 to ± 0.3 %, respectively. These values are determined by several factors including the linearity of the mass spectrometers and the individual blank and memory components. 2 1. ABSTRACT......................................................................................................................
    [Show full text]
  • Evolution of Helium and Argon at a Volcanic Geothermal Reservoir
    PROCEEDINGS, Twenty-Eighth Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, California, January 27-29, 2003 SGP-TR-173 EVOLUTION OF HELIUM AND ARGON AT A VOLCANIC GEOTHERMAL RESERVOIR Mario-César Suárez Arriaga (1) , Fernando Samaniego V. (2) and Enrique Tello H. (3) (1) Faculty of Sciences - Michoacan University (UMSNH) e-mail: [email protected] (2) Faculty of Engineering - National University of Mexico (UNAM) e-mail: [email protected] (3) Comision Federal de Electricidad - (CFE) e-mail: [email protected] Morelia, Mich., 58090, Mexico (He 5.4 ppm, Ne 18 ppm, Ar 0.93% in air at sea ABSTRACT level). 36Ar, Kr and Ne are not produced from rocks but act as atmospheric tracers. Natural rich sources of Vapor phase at volcanic reservoirs has a 3He exist only in the mantle below the Earth’s crust heterogeneous composition, showing very often a indicating magmatic sources. 40Ar, He, 222Rn and wide range of non-condensible gases (NCG) 136Xe are continuously created from radioactive concentration. For example, the chemistry of fluids in decay of U, Th and 40K existent in the Earth’s deep the Los Azufres, Mexico geothermal field originated rocks (Ellis & Mahon, 1977). The presence of two of from volcanic processes and is controlled by those gases, Helium and Argon, has been detected temperatures at depth, mineral solubility, pH values and routinely measured during the last 20 years in the and mineral equilibrium. The NCG concentration at Los Azufres geothermal reservoir; although there are this field ranges between 1% and 9% of total gas also Ne, Kr and Xe (Prasolov et al., 1999; Barragán weight in the steam phase, and it typically contains et al., 2000), these gases are not measured nor CO2 , H2S, NH3 , CH4 , O2 , H2 , N2, He and Ar.
    [Show full text]
  • Facts About Helium by Stephanie Pappas, Live Science Contributor | January 26, 2015 11:50Pm ET
    Facts About Helium By Stephanie Pappas, Live Science Contributor | January 26, 2015 11:50pm ET First discovered in the corona surrounding the sun and later found in gases leaking from Mount Vesuvius, helium is the second-most abundant element in the universe. The second element on the Periodic Table of Elements is inert, colorless and odorless — but far from boring. Helium shows up in semiconductors, birthday balloons and the Large Hadron Collider. Because of its extremely low density, helium floats in air. The low density is also responsible for the weird "squeaky voice" effect when helium is inhaled. The less dense the gas surrounding the vocal cords, the faster they vibrate, sending the voice's pitch skyward. (Practice this party trick in moderation, though: Helium replaces oxygen in the lungs and can kill you if you inhale enough.) Read on for more about this lighter-than-air gas, its amazing discovery story and all of its myriad uses today. Just the facts According to the Jefferson National Linear Accelerator Laboratory, the properties of helium are: Atomic number (number of protons in the nucleus): 2 Atomic symbol (on the Periodic Table of Elements): He Atomic weight (average mass of the atom): 4.002602 Density: 0.0001785 grams per cubic centimeter Phase at Room temperature: Gas Melting point: minus 458.0 degrees Fahrenheit (minus 272.2 degrees Celsius) Boiling point: minus 452.07 F (minus 268.93 C) Number of isotopes (atoms of the same element with a different number of neutrons): 8; 2 stable Most common isotopes: He-4 (99.999866 percent natural abundance) and He-3 (0.000134 percent natural abundance) Solar discovery On Aug.
    [Show full text]
  • The Elements.Pdf
    A Periodic Table of the Elements at Los Alamos National Laboratory Los Alamos National Laboratory's Chemistry Division Presents Periodic Table of the Elements A Resource for Elementary, Middle School, and High School Students Click an element for more information: Group** Period 1 18 IA VIIIA 1A 8A 1 2 13 14 15 16 17 2 1 H IIA IIIA IVA VA VIAVIIA He 1.008 2A 3A 4A 5A 6A 7A 4.003 3 4 5 6 7 8 9 10 2 Li Be B C N O F Ne 6.941 9.012 10.81 12.01 14.01 16.00 19.00 20.18 11 12 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 3 Na Mg IIIB IVB VB VIB VIIB ------- VIII IB IIB Al Si P S Cl Ar 22.99 24.31 3B 4B 5B 6B 7B ------- 1B 2B 26.98 28.09 30.97 32.07 35.45 39.95 ------- 8 ------- 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 4 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 39.10 40.08 44.96 47.88 50.94 52.00 54.94 55.85 58.47 58.69 63.55 65.39 69.72 72.59 74.92 78.96 79.90 83.80 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5 Rb Sr Y Zr NbMo Tc Ru Rh PdAgCd In Sn Sb Te I Xe 85.47 87.62 88.91 91.22 92.91 95.94 (98) 101.1 102.9 106.4 107.9 112.4 114.8 118.7 121.8 127.6 126.9 131.3 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 6 Cs Ba La* Hf Ta W Re Os Ir Pt AuHg Tl Pb Bi Po At Rn 132.9 137.3 138.9 178.5 180.9 183.9 186.2 190.2 190.2 195.1 197.0 200.5 204.4 207.2 209.0 (210) (210) (222) 87 88 89 104 105 106 107 108 109 110 111 112 114 116 118 7 Fr Ra Ac~RfDb Sg Bh Hs Mt --- --- --- --- --- --- (223) (226) (227) (257) (260) (263) (262) (265) (266) () () () () () () http://pearl1.lanl.gov/periodic/ (1 of 3) [5/17/2001 4:06:20 PM] A Periodic Table of the Elements at Los Alamos National Laboratory 58 59 60 61 62 63 64 65 66 67 68 69 70 71 Lanthanide Series* Ce Pr NdPmSm Eu Gd TbDyHo Er TmYbLu 140.1 140.9 144.2 (147) 150.4 152.0 157.3 158.9 162.5 164.9 167.3 168.9 173.0 175.0 90 91 92 93 94 95 96 97 98 99 100 101 102 103 Actinide Series~ Th Pa U Np Pu AmCmBk Cf Es FmMdNo Lr 232.0 (231) (238) (237) (242) (243) (247) (247) (249) (254) (253) (256) (254) (257) ** Groups are noted by 3 notation conventions.
    [Show full text]