2014 09 Bernays 2 Presentation.Key
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester. -

Pure Mathematics
Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture. -

The Development of Mathematical Logic from Russell to Tarski: 1900–1935
The Development of Mathematical Logic from Russell to Tarski: 1900–1935 Paolo Mancosu Richard Zach Calixto Badesa The Development of Mathematical Logic from Russell to Tarski: 1900–1935 Paolo Mancosu (University of California, Berkeley) Richard Zach (University of Calgary) Calixto Badesa (Universitat de Barcelona) Final Draft—May 2004 To appear in: Leila Haaparanta, ed., The Development of Modern Logic. New York and Oxford: Oxford University Press, 2004 Contents Contents i Introduction 1 1 Itinerary I: Metatheoretical Properties of Axiomatic Systems 3 1.1 Introduction . 3 1.2 Peano’s school on the logical structure of theories . 4 1.3 Hilbert on axiomatization . 8 1.4 Completeness and categoricity in the work of Veblen and Huntington . 10 1.5 Truth in a structure . 12 2 Itinerary II: Bertrand Russell’s Mathematical Logic 15 2.1 From the Paris congress to the Principles of Mathematics 1900–1903 . 15 2.2 Russell and Poincar´e on predicativity . 19 2.3 On Denoting . 21 2.4 Russell’s ramified type theory . 22 2.5 The logic of Principia ......................... 25 2.6 Further developments . 26 3 Itinerary III: Zermelo’s Axiomatization of Set Theory and Re- lated Foundational Issues 29 3.1 The debate on the axiom of choice . 29 3.2 Zermelo’s axiomatization of set theory . 32 3.3 The discussion on the notion of “definit” . 35 3.4 Metatheoretical studies of Zermelo’s axiomatization . 38 4 Itinerary IV: The Theory of Relatives and Lowenheim’s¨ Theorem 41 4.1 Theory of relatives and model theory . 41 4.2 The logic of relatives . -
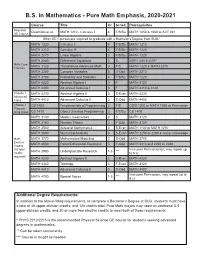
B.S. in Mathematics - Pure Math Emphasis, 2020-2021
B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr. -

Equivalents to the Axiom of Choice and Their Uses A
EQUIVALENTS TO THE AXIOM OF CHOICE AND THEIR USES A Thesis Presented to The Faculty of the Department of Mathematics California State University, Los Angeles In Partial Fulfillment of the Requirements for the Degree Master of Science in Mathematics By James Szufu Yang c 2015 James Szufu Yang ALL RIGHTS RESERVED ii The thesis of James Szufu Yang is approved. Mike Krebs, Ph.D. Kristin Webster, Ph.D. Michael Hoffman, Ph.D., Committee Chair Grant Fraser, Ph.D., Department Chair California State University, Los Angeles June 2015 iii ABSTRACT Equivalents to the Axiom of Choice and Their Uses By James Szufu Yang In set theory, the Axiom of Choice (AC) was formulated in 1904 by Ernst Zermelo. It is an addition to the older Zermelo-Fraenkel (ZF) set theory. We call it Zermelo-Fraenkel set theory with the Axiom of Choice and abbreviate it as ZFC. This paper starts with an introduction to the foundations of ZFC set the- ory, which includes the Zermelo-Fraenkel axioms, partially ordered sets (posets), the Cartesian product, the Axiom of Choice, and their related proofs. It then intro- duces several equivalent forms of the Axiom of Choice and proves that they are all equivalent. In the end, equivalents to the Axiom of Choice are used to prove a few fundamental theorems in set theory, linear analysis, and abstract algebra. This paper is concluded by a brief review of the work in it, followed by a few points of interest for further study in mathematics and/or set theory. iv ACKNOWLEDGMENTS Between the two department requirements to complete a master's degree in mathematics − the comprehensive exams and a thesis, I really wanted to experience doing a research and writing a serious academic paper. -

Forcing in Proof Theory∗
Forcing in proof theory¤ Jeremy Avigad November 3, 2004 Abstract Paul Cohen's method of forcing, together with Saul Kripke's related semantics for modal and intuitionistic logic, has had profound e®ects on a number of branches of mathematical logic, from set theory and model theory to constructive and categorical logic. Here, I argue that forcing also has a place in traditional Hilbert-style proof theory, where the goal is to formalize portions of ordinary mathematics in restricted axiomatic theories, and study those theories in constructive or syntactic terms. I will discuss the aspects of forcing that are useful in this respect, and some sample applications. The latter include ways of obtaining conservation re- sults for classical and intuitionistic theories, interpreting classical theories in constructive ones, and constructivizing model-theoretic arguments. 1 Introduction In 1963, Paul Cohen introduced the method of forcing to prove the indepen- dence of both the axiom of choice and the continuum hypothesis from Zermelo- Fraenkel set theory. It was not long before Saul Kripke noted a connection be- tween forcing and his semantics for modal and intuitionistic logic, which had, in turn, appeared in a series of papers between 1959 and 1965. By 1965, Scott and Solovay had rephrased Cohen's forcing construction in terms of Boolean-valued models, foreshadowing deeper algebraic connections between forcing, Kripke se- mantics, and Grothendieck's notion of a topos of sheaves. In particular, Lawvere and Tierney were soon able to recast Cohen's original independence proofs as sheaf constructions.1 It is safe to say that these developments have had a profound impact on most branches of mathematical logic. -

Introduction: the 1930S Revolution
PROPERTY OF MIT PRESS: FOR PROOFREADING AND INDEXING PURPOSES ONLY Introduction: The 1930s Revolution The theory of computability was launched in the 1930s by a group of young math- ematicians and logicians who proposed new, exact, characterizations of the idea of algorithmic computability. The most prominent of these young iconoclasts were Kurt Gödel, Alonzo Church, and Alan Turing. Others also contributed to the new field, most notably Jacques Herbrand, Emil Post, Stephen Kleene, and J. Barkley Rosser. This seminal research not only established the theoretical basis for computability: these key thinkers revolutionized and reshaped the mathematical world—a revolu- tion that culminated in the Information Age. Their motive, however, was not to pioneer the discipline that we now know as theoretical computer science, although with hindsight this is indeed what they did. Nor was their motive to design electronic digital computers, although Turing did go on to do so (in fact producing the first complete paper design that the world had seen for an electronic stored-program universal computer). Their work was rather the continuation of decades of intensive investigation into that most abstract of subjects, the foundations of mathematics—investigations carried out by such great thinkers as Leopold Kronecker, Richard Dedekind, Gottlob Frege, Bertrand Russell, David Hilbert, L. E. J. Brouwer, Paul Bernays, and John von Neumann. The concept of an algorithm, or an effective or computable procedure, was central during these decades of foundational study, although for a long time no attempt was made to characterize the intuitive concept formally. This changed when Hilbert’s foundation- alist program, and especially the issue of decidability, made it imperative to provide an exact characterization of the idea of a computable function—or algorithmically calculable function, or effectively calculable function, or decidable predicate. -

Gödel on Finitism, Constructivity and Hilbert's Program
Lieber Herr Bernays!, Lieber Herr Gödel! Gödel on finitism, constructivity and Hilbert’s program Solomon Feferman 1. Gödel, Bernays, and Hilbert. The correspondence between Paul Bernays and Kurt Gödel is one of the most extensive in the two volumes of Gödel’s collected works devoted to his letters of (primarily) scientific, philosophical and historical interest. It ranges from 1930 to 1975 and deals with a rich body of logical and philosophical issues, including the incompleteness theorems, finitism, constructivity, set theory, the philosophy of mathematics, and post- Kantian philosophy, and contains Gödel’s thoughts on many topics that are not expressed elsewhere. In addition, it testifies to their life-long warm personal relationship. I have given a detailed synopsis of the Bernays Gödel correspondence, with explanatory background, in my introductory note to it in Vol. IV of Gödel’s Collected Works, pp. 41- 79.1 My purpose here is to focus on only one group of interrelated topics from these exchanges, namely the light that ittogether with assorted published and unpublished articles and lectures by Gödelthrows on his perennial preoccupations with the limits of finitism, its relations to constructivity, and the significance of his incompleteness theorems for Hilbert’s program.2 In that connection, this piece has an important subtext, namely the shadow of Hilbert that loomed over Gödel from the beginning to the end of his career. 1 The five volumes of Gödel’s Collected Works (1986-2003) are referred to below, respectively, as CW I, II, III, IV and V. CW I consists of the publications 1929-1936, CW II of the publications 1938-1974, CW III of unpublished essays and letters, CW IV of correspondence A-G, and CW V of correspondence H-Z. -

Axiomatic Foundations of Mathematics Ryan Melton Dr
Axiomatic Foundations of Mathematics Ryan Melton Dr. Clint Richardson, Faculty Advisor Stephen F. Austin State University As Bertrand Russell once said, Gödel's Method Pure mathematics is the subject in which we Consider the expression First, Gödel assigned a unique natural number to do not know what we are talking about, or each of the logical symbols and numbers. 2 + 3 = 5 whether what we are saying is true. Russell’s statement begs from us one major This expression is mathematical; it belongs to the field For example: if the symbol '0' corresponds to we call arithmetic and is composed of basic arithmetic question: the natural number 1, '+' to 2, and '=' to 3, then symbols. '0 = 0' '0 + 0 = 0' What is Mathematics founded on? On the other hand, the sentence and '2 + 3 = 5' is an arithmetical formula. 1 3 1 1 2 1 3 1 so each expression corresponds to a sequence. Axioms and Axiom Systems is metamathematical; it is constructed outside of mathematics and labels the expression above as a Then, for this new sequence x1x2x3…xn of formula in arithmetic. An axiom is a belief taken without proof, and positive integers, we associate a Gödel number thus an axiom system is a set of beliefs as follows: x1 x2 x3 xn taken without proof. enc( x1x2x3...xn ) = 2 3 5 ... pn Since Principia Mathematica was such a bold where the encoding is the product of n factors, Consistent? Complete? leap in the right direction--although proving each of which is found by raising the j-th prime nothing about consistency--several attempts at to the xj power. -

Hunting the Story of Moses Schönfinkel
Where Did Combinators Come From? Hunting the Story of Moses Schönfinkel Stephen Wolfram* Combinators were a key idea in the development of mathematical logic and the emergence of the concept of universal computation. They were introduced on December 7, 1920, by Moses Schönfinkel. This is an exploration of the personal story and intellectual context of Moses Schönfinkel, including extensive new research based on primary sources. December 7, 1920 On Tuesday, December 7, 1920, the Göttingen Mathematics Society held its regular weekly meeting—at which a 32-year-old local mathematician named Moses Schönfinkel with no known previous mathematical publications gave a talk entitled “Elemente der Logik” (“Elements of Logic”). This piece is included in S. Wolfram (2021), Combinators: A Centennial View, Wolfram Media. (wolframmedia.com/products/combinators-a-centennial-view.html) and accompanies arXiv:2103.12811 and arXiv:2102.09658. Originally published December 7, 2020 *Email: [email protected] 2 | Stephen Wolfram A hundred years later what was presented in that talk still seems in many ways alien and futuristic—and for most people almost irreducibly abstract. But we now realize that that talk gave the first complete formalism for what is probably the single most important idea of this past century: the idea of universal computation. Sixteen years later would come Turing machines (and lambda calculus). But in 1920 Moses Schönfinkel presented what he called “building blocks of logic”—or what we now call “combinators”—and then proceeded to show that by appropriately combining them one could effectively define any function, or, in modern terms, that they could be used to do universal computation. -

MATH S121 a Foundation in Pure Mathematics (Free Courseware) © the Open University of Hong Kong
MATH S121 A Foundation In Pure Mathematics (Free Courseware) © The Open University of Hong Kong This work is licensed under a Creative Commons-ShareAlike 4.0 International License Contents Chapter 1 Counting and Basic Probability ..................................................................1 1.1 About this module..............................................................................................................1 1.2 Introduction ........................................................................................................................2 1.3 Counting .............................................................................................................................2 1.3.1 Number of outcomes of an event .........................................................................2 1.3.2 Addition Principle ....................................................................................................3 1.3.3 Multiplication Principle ...........................................................................................4 1.3.4 Permutations and combinations...........................................................................6 1.3.4.1 Permutation..................................................................................................7 1.3.4.2 Activity 1 .......................................................................................................8 1.3.4.2.1 Activity 1 feedback ............................................................................8 1.3.4.3 Combinations ...............................................................................................8 -

The Foundations of Mathematics, in Accordance with the General Method of Frege, Whitehead, and Bussell
$88 F. P. KAMSEY [NOV. 12, THK FOUNDATIONS OF MATHEMATICS By F. P. KAMSEY. [Received 23 August, 1925.—Read 12 November, 1925.] Preface. THE object of this paper is to give a satisfactory account of the Foundations of Mathematics, in accordance with the general method of Frege, Whitehead, and Bussell. Following these authorities, I hold that mathematics is part of logic, and so belong to what may be called the logical school as opposed to the formalist and intuitionist schools. I have therefore taken Principia Mathematica as a basis for discussion and amendment, and believe myself to have discovered how, by using the work of Mr. Ludwig Wittgenstein, it can be rendered free from the serious objections which have caused its rejection by the majority of German authorities.who have deserted altogether its line of approach. Contents. I. Introduction. II. Principia Matliematica. III. Predicative Functions. IV. Functions in Extension. V. The Axioms. I. Introduction. In this chapter we shall be concerned with the general nature of pure mathematics*, and how it is distinguished from other sciences. • In future by "mathematics " will always be meant " pure mathematics." 1925.] THE FOUNDATIONS OF MATHEMATICS. 889 Here there are really two distinct categories of things of which an account must be given, the ideas or concepts of mathematics, and the propositions of mathematics. This distinction is neither artificial nor unnecessary, for the great majority of writers on the subject have con- centrated their attention on the explanation of one or other of these categories, and erroneously supposed that a satisfactory explanation of the other would immediately follow.