Physical Model of Asteroid 1620 Geographos from Radar and Optical Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Minor Planet Bulletin
THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 36, NUMBER 3, A.D. 2009 JULY-SEPTEMBER 77. PHOTOMETRIC MEASUREMENTS OF 343 OSTARA Our data can be obtained from http://www.uwec.edu/physics/ AND OTHER ASTEROIDS AT HOBBS OBSERVATORY asteroid/. Lyle Ford, George Stecher, Kayla Lorenzen, and Cole Cook Acknowledgements Department of Physics and Astronomy University of Wisconsin-Eau Claire We thank the Theodore Dunham Fund for Astrophysics, the Eau Claire, WI 54702-4004 National Science Foundation (award number 0519006), the [email protected] University of Wisconsin-Eau Claire Office of Research and Sponsored Programs, and the University of Wisconsin-Eau Claire (Received: 2009 Feb 11) Blugold Fellow and McNair programs for financial support. References We observed 343 Ostara on 2008 October 4 and obtained R and V standard magnitudes. The period was Binzel, R.P. (1987). “A Photoelectric Survey of 130 Asteroids”, found to be significantly greater than the previously Icarus 72, 135-208. reported value of 6.42 hours. Measurements of 2660 Wasserman and (17010) 1999 CQ72 made on 2008 Stecher, G.J., Ford, L.A., and Elbert, J.D. (1999). “Equipping a March 25 are also reported. 0.6 Meter Alt-Azimuth Telescope for Photometry”, IAPPP Comm, 76, 68-74. We made R band and V band photometric measurements of 343 Warner, B.D. (2006). A Practical Guide to Lightcurve Photometry Ostara on 2008 October 4 using the 0.6 m “Air Force” Telescope and Analysis. Springer, New York, NY. located at Hobbs Observatory (MPC code 750) near Fall Creek, Wisconsin. -

1620 Geographos and 433 Eros: Shaped by Planetary Tides?
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server 1620 Geographos and 433 Eros: Shaped by Planetary Tides? W. F. Bottke, Jr. Center for Radiophysics and Space Research, Cornell University, Ithaca, NY 14853-6801 D. C. Richardson Department of Astronomy, University of Washington, Box 351580, Seattle, WA 98195 P. Michel Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy and S. G. Love Jet Propulsion Laboratory, California Institute of Technology, M/S 306-438, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 Received 23 September 1998; accepted 10 December 1998 –2– ABSTRACT Until recently, most asteroids were thought to be solid bodies whose shapes were determined largely by collisions with other asteroids (Davis et al., 1989). It now seems that many asteroids are little more than rubble piles, held together by self-gravity (Burns 1998); this means that their shapes may be strongly distorted by tides during close encounters with planets. Here we report on numerical simulations of encounters between a ellipsoid-shaped rubble-pile asteroid and the Earth. After an encounter, many of the simulated asteroids develop the same rotation rate and distinctive shape (i.e., highly elongated with a single convex side, tapered ends, and small protuberances swept back against the rotation direction) as 1620 Geographos. Since our numerical studies show that these events occur with some frequency, we suggest that Geographos may be a tidally distorted object. In addition, our work shows that 433 Eros, which will be visited by the NEAR spacecraft in 1999, is much like Geographos, which suggests that it too may have been molded by tides in the past. -

Radar Observations of Asteroid 1620 Geographos
ICARUS 121, 46±66 (1996) ARTICLE NO. 0071 Radar Observations of Asteroid 1620 Geographos STEVEN J. OSTRO,RAYMOND F. JURGENS, AND KEITH D. ROSEMA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California 91109±8099 E-mail: [email protected] R. SCOTT HUDSON School of Electrical Engineering and Computer Science, Washington State University, Pullman, Washington 99164±2752 AND JON D. GIORGINI,RON WINKLER,DONALD K. YEOMANS,DENNIS CHOATE,RANDY ROSE,MARTIN A. SLADE, S. DENISE HOWARD,DANIEL J. SCHEERES, AND DAVID L. MITCHELL Jet Propulsion Laboratory, Pasadena, California 91109±8099 Received July 31, 1995; revised October 30, 1995 1. INTRODUCTION Goldstone radar observations of Geographos from August 28 through September 2, 1994 yield over 400 delay-Doppler images whose linear spatial resolutions range from p75 to Asteroid 1620 Geographos was discovered in 1951 by p151 m, and 138 pairs of dual-polarization (OC, SC) spectra A. G. Wilson and R. Minkowski and was observed over with one-dimensional resolution of 103 m. Each data type an eight-month interval in 1969 by Dunlap (1974) for ``light provides thorough rotational coverage. The images contain variation, colors, and polarization.'' From his analysis, an intrinsic north/south ambiguity, but the equatorial view which included experiments with laboratory models (Dun- allows accurate determination of the shape of the radar- lap 1972), he estimated the asteroid's spin vector and geo- facing part of the asteroid's pole-on silhouette at any rotation metric albedo, and noted that ``the best ®tting model (a phase. Sums of co-registered images that cover nearly a full cylinder with hemispherical ends) had a length to width rotation have de®ned the extremely elongated shape of that ratio of 2.7, which results in Geographos being 1.50 6 0.15 silhouette (S. -

Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre -

The Minor Planet Bulletin
THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 35, NUMBER 3, A.D. 2008 JULY-SEPTEMBER 95. ASTEROID LIGHTCURVE ANALYSIS AT SCT/ST-9E, or 0.35m SCT/STL-1001E. Depending on the THE PALMER DIVIDE OBSERVATORY: binning used, the scale for the images ranged from 1.2-2.5 DECEMBER 2007 – MARCH 2008 arcseconds/pixel. Exposure times were 90–240 s. Most observations were made with no filter. On occasion, e.g., when a Brian D. Warner nearly full moon was present, an R filter was used to decrease the Palmer Divide Observatory/Space Science Institute sky background noise. Guiding was used in almost all cases. 17995 Bakers Farm Rd., Colorado Springs, CO 80908 [email protected] All images were measured using MPO Canopus, which employs differential aperture photometry to determine the values used for (Received: 6 March) analysis. Period analysis was also done using MPO Canopus, which incorporates the Fourier analysis algorithm developed by Harris (1989). Lightcurves for 17 asteroids were obtained at the Palmer Divide Observatory from December 2007 to early The results are summarized in the table below, as are individual March 2008: 793 Arizona, 1092 Lilium, 2093 plots. The data and curves are presented without comment except Genichesk, 3086 Kalbaugh, 4859 Fraknoi, 5806 when warranted. Column 3 gives the full range of dates of Archieroy, 6296 Cleveland, 6310 Jankonke, 6384 observations; column 4 gives the number of data points used in the Kervin, (7283) 1989 TX15, 7560 Spudis, (7579) 1990 analysis. Column 5 gives the range of phase angles. -

Appendix 1 1311 Discoverers in Alphabetical Order
Appendix 1 1311 Discoverers in Alphabetical Order Abe, H. 28 (8) 1993-1999 Bernstein, G. 1 1998 Abe, M. 1 (1) 1994 Bettelheim, E. 1 (1) 2000 Abraham, M. 3 (3) 1999 Bickel, W. 443 1995-2010 Aikman, G. C. L. 4 1994-1998 Biggs, J. 1 2001 Akiyama, M. 16 (10) 1989-1999 Bigourdan, G. 1 1894 Albitskij, V. A. 10 1923-1925 Billings, G. W. 6 1999 Aldering, G. 4 1982 Binzel, R. P. 3 1987-1990 Alikoski, H. 13 1938-1953 Birkle, K. 8 (8) 1989-1993 Allen, E. J. 1 2004 Birtwhistle, P. 56 2003-2009 Allen, L. 2 2004 Blasco, M. 5 (1) 1996-2000 Alu, J. 24 (13) 1987-1993 Block, A. 1 2000 Amburgey, L. L. 2 1997-2000 Boattini, A. 237 (224) 1977-2006 Andrews, A. D. 1 1965 Boehnhardt, H. 1 (1) 1993 Antal, M. 17 1971-1988 Boeker, A. 1 (1) 2002 Antolini, P. 4 (3) 1994-1996 Boeuf, M. 12 1998-2000 Antonini, P. 35 1997-1999 Boffin, H. M. J. 10 (2) 1999-2001 Aoki, M. 2 1996-1997 Bohrmann, A. 9 1936-1938 Apitzsch, R. 43 2004-2009 Boles, T. 1 2002 Arai, M. 45 (45) 1988-1991 Bonomi, R. 1 (1) 1995 Araki, H. 2 (2) 1994 Borgman, D. 1 (1) 2004 Arend, S. 51 1929-1961 B¨orngen, F. 535 (231) 1961-1995 Armstrong, C. 1 (1) 1997 Borrelly, A. 19 1866-1894 Armstrong, M. 2 (1) 1997-1998 Bourban, G. 1 (1) 2005 Asami, A. 7 1997-1999 Bourgeois, P. 1 1929 Asher, D. -
![Arxiv:2108.13954V1 [Hep-Ph] 31 Aug 2021](https://docslib.b-cdn.net/cover/1443/arxiv-2108-13954v1-hep-ph-31-aug-2021-2901443.webp)
Arxiv:2108.13954V1 [Hep-Ph] 31 Aug 2021
Is backreaction in cosmology a relativistic effect? On the need for an extension of Newton’s theory to non-Euclidean topologies Quentin Vigneron1,2 1 Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University, Grudziadzka 5, 87-100 Toru´n, Poland 2 Univ Lyon, Ens de Lyon, Univ Lyon1, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, F–69007, Lyon, France E-mail: [email protected], [email protected] 22 September 2021 Abstract. Cosmological backreaction corresponds to the effect of inhomogeneities of structure on the global expansion of the Universe. The main question surrounding this phenomenon is whether or not it could explain the recent acceleration of the scale factor, also known as Dark Energy. One of the most important result on this subject is the Buchert-Ehlers theorem (Buchert & Ehlers, 1997) stating that backreaction is exactly zero when calculated using Newton’s theory of gravitation, which may not be the case in general relativity. It is generally said that this result implies that backreaction is a purely relativistic effect. We will show that this is not necessarily the case, in the sense that this implication does not apply to a universe which is still well described by Newton’s theory on small scales but has a non-Euclidean topology. The theorem should therefore be generalised to account for such a scenario. In a heuristic calculation where we define a theory which is locally Newtonian but defined on a non-Euclidean topology, we show that backreaction is non-zero, meaning that it arXiv:2109.10336v1 [gr-qc] 21 Sep 2021 might be non-relativistic and might depend on the topology of our Universe. -

1620 Geographos and 433 Eros: Shaped by Planetary Tides?
1620 Geographos and 433 Eros: Shaped by Planetary Tides? W. F. Bottke, Jr. Center for Radiophysics and Space Research, Cornell University, Ithaca, NY 14853-6801 D. C. Richardson Department of Astronomy, University of Washington, Box 351580, Seattle, WA 98195 P. Michel Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy and S. G. Love Jet Propulsion Laboratory, California Institute of Technology, M/S 306-438, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 Received 23 September 1998; accepted 10 December 1998 arXiv:astro-ph/9812235v1 11 Dec 1998 –2– ABSTRACT Until recently, most asteroids were thought to be solid bodies whose shapes were determined largely by collisions with other asteroids (Davis et al., 1989). It now seems that many asteroids are little more than rubble piles, held together by self-gravity (Burns 1998); this means that their shapes may be strongly distorted by tides during close encounters with planets. Here we report on numerical simulations of encounters between a ellipsoid-shaped rubble-pile asteroid and the Earth. After an encounter, many of the simulated asteroids develop the same rotation rate and distinctive shape (i.e., highly elongated with a single convex side, tapered ends, and small protuberances swept back against the rotation direction) as 1620 Geographos. Since our numerical studies show that these events occur with some frequency, we suggest that Geographos may be a tidally distorted object. In addition, our work shows that 433 Eros, which will be visited by the NEAR spacecraft in 1999, is much like Geographos, which suggests that it too may have been molded by tides in the past. -

Appendix 1 897 Discoverers in Alphabetical Order
Appendix 1 897 Discoverers in Alphabetical Order Abe, H. 22 (7) 1993-1999 Bohrmann, A. 9 1936-1938 Abraham, M. 3 (3) 1999 Bonomi, R. 1 (1) 1995 Aikman, G. C. L. 3 1994-1997 B¨orngen, F. 437 (161) 1961-1995 Akiyama, M. 14 (10) 1989-1999 Borrelly, A. 19 1866-1894 Albitskij, V. A. 10 1923-1925 Bourgeois, P. 1 1929 Aldering, G. 3 1982 Bowell, E. 563 (6) 1977-1994 Alikoski, H. 13 1938-1953 Boyer, L. 40 1930-1952 Alu, J. 20 (11) 1987-1993 Brady, J. L. 1 1952 Amburgey, L. L. 1 1997 Brady, N. 1 2000 Andrews, A. D. 1 1965 Brady, S. 1 1999 Antal, M. 17 1971-1988 Brandeker, A. 1 2000 Antonini, P. 25 (1) 1996-1999 Brcic, V. 2 (2) 1995 Aoki, M. 1 1996 Broughton, J. 179 1997-2002 Arai, M. 43 (43) 1988-1991 Brown, J. A. 1 (1) 1990 Arend, S. 51 1929-1961 Brown, M. E. 1 (1) 2002 Armstrong, C. 1 (1) 1997 Broˇzek, L. 23 1979-1982 Armstrong, M. 2 (1) 1997-1998 Bruton, J. 1 1997 Asami, A. 5 1997-1999 Bruton, W. D. 2 (2) 1999-2000 Asher, D. J. 9 1994-1995 Bruwer, J. A. 4 1953-1970 Augustesen, K. 26 (26) 1982-1987 Buchar, E. 1 1925 Buie, M. W. 13 (1) 1997-2001 Baade, W. 10 1920-1949 Buil, C. 4 1997 Babiakov´a, U. 4 (4) 1998-2000 Burleigh, M. R. 1 (1) 1998 Bailey, S. I. 1 1902 Burnasheva, B. A. 13 1969-1971 Balam, D. -
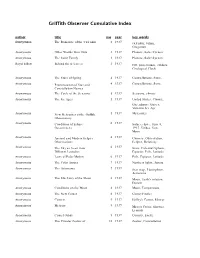
Griffith Observer Cumulative Index
Griffith Observer Cumulative Index author title mo year key words Anonymous The Romance of the Calendar 2 1937 calendar, Julian, Gregorian Anonymous Other Worlds than Ours 3 1937 Planets, Solar System Anonymous The S ola r Fa mily 3 1937 Planets, Solar System Roya l Elliott Behind the Sciences 3 1937 GO, pla ne ta rium, e xhibits , Ge ologica l Clock Anonymous The Stars of Spring 4 1937 Cons te lla tions , S ta rs , Anonymous Pronunciation of Star and 4 1937 Cons te lla tions , S ta rs Constellation Names Anonymous The Cycle of the Seasons 5 1937 Seasons, climate Anonymous The Ice Ages 5 1937 United States, Climate, Greenhouse Gases, Volcano, Ice Age Anonymous New Meteorites at the Griffith 5 1937 Meteorites Observatory Anonymous Conditions of Eclipse 6 1937 Solar eclipse, June 8, Occurrences 1937, Umbra, Sun, Moon Anonymous Ancient and Modern Eclipse 6 1937 Chinese, Observation, Observations Eclips e , Re la tivity Anonymous The Sky as Seen from 6 1937 Stars, Celestial Sphere, Different Latitudes Equator, Pole, Latitude Anonymous Laws of Polar Motion 6 1937 Pole, Equator, Latitude Anonymous The Polar Aurora 7 1937 Northern lights, Aurora Anonymous The Astrorama 7 1937 Star map, Planisphere, Astrorama Anonymous The Life Story of the Moon 8 1937 Moon, Earth's rotation, Darwin Anonymous Conditions on the Moon 8 1937 Moon, Temperature, Anonymous The New Comet 8 1937 Come t Fins le r Anonymous Comets 9 1937 Halley's Comet, Meteor Anonymous Meteors 9 1937 Meteor Crater, Shower, Leonids Anonymous Comet Orbits 9 1937 Comets, Encke Anonymous -

The Astronomer Magazine Index
The Astronomer Magazine Index The numbers in brackets indicate approx lengths in pages (quarto to 1982 Aug, A4 afterwards) 1964 May p1-2 (1.5) Editorial (Function of CA) p2 (0.3) Retrospective meeting after 2 issues : planned date p3 (1.0) Solar Observations . James Muirden , John Larard p4 (0.9) Domes on the Mare Tranquillitatis . Colin Pither p5 (1.1) Graze Occultation of ZC620 on 1964 Feb 20 . Ken Stocker p6-8 (2.1) Artificial Satellite magnitude estimates : Jan-Apr . Russell Eberst p8-9 (1.0) Notes on Double Stars, Nebulae & Clusters . John Larard & James Muirden p9 (0.1) Venus at half phase . P B Withers p9 (0.1) Observations of Echo I, Echo II and Mercury . John Larard p10 (1.0) Note on the first issue 1964 Jun p1-2 (2.0) Editorial (Poor initial response, Magazine name comments) p3-4 (1.2) Jupiter Observations . Alan Heath p4-5 (1.0) Venus Observations . Alan Heath , Colin Pither p5 (0.7) Remarks on some observations of Venus . Colin Pither p5-6 (0.6) Atlas Coeli corrections (5 stars) . George Alcock p6 (0.6) Telescopic Meteors . George Alcock p7 (0.6) Solar Observations . John Larard p7 (0.3) R Pegasi Observations . John Larard p8 (1.0) Notes on Clusters & Double Stars . John Larard p9 (0.1) LQ Herculis bright . George Alcock p10 (0.1) Observations of 2 fireballs . John Larard 1964 Jly p2 (0.6) List of Members, Associates & Affiliations p3-4 (1.1) Editorial (Need for more members) p4 (0.2) Summary of June 19 meeting p4 (0.5) Exploding Fireball of 1963 Sep 12/13 . -

Solar Radiation and Near-Earth Asteroids: Thermophysical Modeling and New Measurements of the Yarkovsky Effect
University of California Los Angeles Solar Radiation and Near-Earth Asteroids: Thermophysical Modeling and New Measurements of the Yarkovsky Effect A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Geophysics and Space Physics by Carolyn Rosemary Nugent 2013 c Copyright by Carolyn Rosemary Nugent 2013 Abstract of the Dissertation Solar Radiation and Near-Earth Asteroids: Thermophysical Modeling and New Measurements of the Yarkovsky Effect by Carolyn Rosemary Nugent Doctor of Philosophy in Geophysics and Space Physics University of California, Los Angeles, 2013 Professor Jean-Luc Margot, Chair This dissertation examines the influence of solar radiation on near-Earth asteroids (NEAs); it investigates thermal properties and examines changes to orbits caused by the process of anisotropic re-radiation of sunlight called the Yarkovsky effect. For the first portion of this dissertation, we used geometric albedos (pV ) and diameters derived from the Wide-Field Infrared Survey Explorer (WISE), as well as geometric albedos and diameters from the literature, to produce more accurate diurnal Yarkovsky drift predic- tions for 540 NEAs out of the current sample of ∼ 8800 known objects. These predictions are intended to assist observers, and should enable future Yarkovsky detections. The second portion of this dissertation introduces a new method for detecting the Yarkovsky drift. We identified and quantified semi-major axis drifts in NEAs by performing orbital fits to optical and radar astrometry of all numbered NEAs. We discuss on a subset of 54 NEAs that exhibit some of the most reliable and strongest drift rates. Our selection criteria include a Yarkovsky sensitivity metric that quantifies the detectability of semi-major axis drift in any given data set, a signal-to-noise metric, and orbital coverage requirements.