Definite Clause Grammars with Parse Trees: Extension for Prolog
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
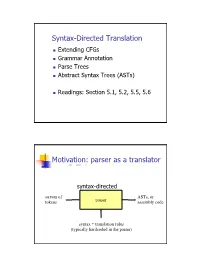
Syntax-Directed Translation, Parse Trees, Abstract Syntax Trees
Syntax-Directed Translation Extending CFGs Grammar Annotation Parse Trees Abstract Syntax Trees (ASTs) Readings: Section 5.1, 5.2, 5.5, 5.6 Motivation: parser as a translator syntax-directed translation stream of ASTs, or tokens parser assembly code syntax + translation rules (typically hardcoded in the parser) 1 Mechanism of syntax-directed translation syntax-directed translation is done by extending the CFG a translation rule is defined for each production given X Æ d A B c the translation of X is defined in terms of translation of nonterminals A, B values of attributes of terminals d, c constants To translate an input string: 1. Build the parse tree. 2. Working bottom-up • Use the translation rules to compute the translation of each nonterminal in the tree Result: the translation of the string is the translation of the parse tree's root nonterminal Why bottom up? a nonterminal's value may depend on the value of the symbols on the right-hand side, so translate a non-terminal node only after children translations are available 2 Example 1: arith expr to its value Syntax-directed translation: the CFG translation rules E Æ E + T E1.trans = E2.trans + T.trans E Æ T E.trans = T.trans T Æ T * F T1.trans = T2.trans * F.trans T Æ F T.trans = F.trans F Æ int F.trans = int.value F Æ ( E ) F.trans = E.trans Example 1 (cont) E (18) Input: 2 * (4 + 5) T (18) T (2) * F (9) F (2) ( E (9) ) int (2) E (4) * T (5) Annotated Parse Tree T (4) F (5) F (4) int (5) int (4) 3 Example 2: Compute type of expr E -> E + E if ((E2.trans == INT) and (E3.trans == INT) then E1.trans = INT else E1.trans = ERROR E -> E and E if ((E2.trans == BOOL) and (E3.trans == BOOL) then E1.trans = BOOL else E1.trans = ERROR E -> E == E if ((E2.trans == E3.trans) and (E2.trans != ERROR)) then E1.trans = BOOL else E1.trans = ERROR E -> true E.trans = BOOL E -> false E.trans = BOOL E -> int E.trans = INT E -> ( E ) E1.trans = E2.trans Example 2 (cont) Input: (2 + 2) == 4 1. -

An Efficient Implementation of the Head-Corner Parser
An Efficient Implementation of the Head-Corner Parser Gertjan van Noord" Rijksuniversiteit Groningen This paper describes an efficient and robust implementation of a bidirectional, head-driven parser for constraint-based grammars. This parser is developed for the OVIS system: a Dutch spoken dialogue system in which information about public transport can be obtained by telephone. After a review of the motivation for head-driven parsing strategies, and head-corner parsing in particular, a nondeterministic version of the head-corner parser is presented. A memorization technique is applied to obtain a fast parser. A goal-weakening technique is introduced, which greatly improves average case efficiency, both in terms of speed and space requirements. I argue in favor of such a memorization strategy with goal-weakening in comparison with ordinary chart parsers because such a strategy can be applied selectively and therefore enormously reduces the space requirements of the parser, while no practical loss in time-efficiency is observed. On the contrary, experiments are described in which head-corner and left-corner parsers imple- mented with selective memorization and goal weakening outperform "standard" chart parsers. The experiments include the grammar of the OV/S system and the Alvey NL Tools grammar. Head-corner parsing is a mix of bottom-up and top-down processing. Certain approaches to robust parsing require purely bottom-up processing. Therefore, it seems that head-corner parsing is unsuitable for such robust parsing techniques. However, it is shown how underspecification (which arises very naturally in a logic programming environment) can be used in the head-corner parser to allow such robust parsing techniques. -

Derivatives of Parsing Expression Grammars
Derivatives of Parsing Expression Grammars Aaron Moss Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, Canada [email protected] This paper introduces a new derivative parsing algorithm for recognition of parsing expression gram- mars. Derivative parsing is shown to have a polynomial worst-case time bound, an improvement on the exponential bound of the recursive descent algorithm. This work also introduces asymptotic analysis based on inputs with a constant bound on both grammar nesting depth and number of back- tracking choices; derivative and recursive descent parsing are shown to run in linear time and constant space on this useful class of inputs, with both the theoretical bounds and the reasonability of the in- put class validated empirically. This common-case constant memory usage of derivative parsing is an improvement on the linear space required by the packrat algorithm. 1 Introduction Parsing expression grammars (PEGs) are a parsing formalism introduced by Ford [6]. Any LR(k) lan- guage can be represented as a PEG [7], but there are some non-context-free languages that may also be represented as PEGs (e.g. anbncn [7]). Unlike context-free grammars (CFGs), PEGs are unambiguous, admitting no more than one parse tree for any grammar and input. PEGs are a formalization of recursive descent parsers allowing limited backtracking and infinite lookahead; a string in the language of a PEG can be recognized in exponential time and linear space using a recursive descent algorithm, or linear time and space using the memoized packrat algorithm [6]. PEGs are formally defined and these algo- rithms outlined in Section 3. -

Modular Logic Grammars
MODULAR LOGIC GRAMMARS Michael C. McCord IBM Thomas J. Watson Research Center P. O. Box 218 Yorktown Heights, NY 10598 ABSTRACT scoping of quantifiers (and more generally focalizers, McCord, 1981) when the building of log- This report describes a logic grammar formalism, ical forms is too closely bonded to syntax. Another Modular Logic Grammars, exhibiting a high degree disadvantage is just a general result of lack of of modularity between syntax and semantics. There modularity: it can be harder to develop and un- is a syntax rule compiler (compiling into Prolog) derstand syntax rules when too much is going on in which takes care of the building of analysis them. structures and the interface to a clearly separated semantic interpretation component dealing with The logic grammars described in McCord (1982, scoping and the construction of logical forms. The 1981) were three-pass systems, where one of the main whole system can work in either a one-pass mode or points of the modularity was a good treatment of a two-pass mode. [n the one-pass mode, logical scoping. The first pass was the syntactic compo- forms are built directly during parsing through nent, written as a definite clause grammar, where interleaved calls to semantics, added automatically syntactic structures were explicitly built up in by the rule compiler. [n the two-pass mode, syn- the arguments of the non-terminals. Word sense tactic analysis trees are built automatically in selection and slot-filling were done in this first the first pass, and then given to the (one-pass) pass, so that the output analysis trees were actu- semantic component. -

Parsing 1. Grammars and Parsing 2. Top-Down and Bottom-Up Parsing 3
Syntax Parsing syntax: from the Greek syntaxis, meaning “setting out together or arrangement.” 1. Grammars and parsing Refers to the way words are arranged together. 2. Top-down and bottom-up parsing Why worry about syntax? 3. Chart parsers • The boy ate the frog. 4. Bottom-up chart parsing • The frog was eaten by the boy. 5. The Earley Algorithm • The frog that the boy ate died. • The boy whom the frog was eaten by died. Slide CS474–1 Slide CS474–2 Grammars and Parsing Need a grammar: a formal specification of the structures allowable in Syntactic Analysis the language. Key ideas: Need a parser: algorithm for assigning syntactic structure to an input • constituency: groups of words may behave as a single unit or phrase sentence. • grammatical relations: refer to the subject, object, indirect Sentence Parse Tree object, etc. Beavis ate the cat. S • subcategorization and dependencies: refer to certain kinds of relations between words and phrases, e.g. want can be followed by an NP VP infinitive, but find and work cannot. NAME V NP All can be modeled by various kinds of grammars that are based on ART N context-free grammars. Beavis ate the cat Slide CS474–3 Slide CS474–4 CFG example CFG’s are also called phrase-structure grammars. CFG’s Equivalent to Backus-Naur Form (BNF). A context free grammar consists of: 1. S → NP VP 5. NAME → Beavis 1. a set of non-terminal symbols N 2. VP → V NP 6. V → ate 2. a set of terminal symbols Σ (disjoint from N) 3. -

Abstract Syntax Trees & Top-Down Parsing
Abstract Syntax Trees & Top-Down Parsing Review of Parsing • Given a language L(G), a parser consumes a sequence of tokens s and produces a parse tree • Issues: – How do we recognize that s ∈ L(G) ? – A parse tree of s describes how s ∈ L(G) – Ambiguity: more than one parse tree (possible interpretation) for some string s – Error: no parse tree for some string s – How do we construct the parse tree? Compiler Design 1 (2011) 2 Abstract Syntax Trees • So far, a parser traces the derivation of a sequence of tokens • The rest of the compiler needs a structural representation of the program • Abstract syntax trees – Like parse trees but ignore some details – Abbreviated as AST Compiler Design 1 (2011) 3 Abstract Syntax Trees (Cont.) • Consider the grammar E → int | ( E ) | E + E • And the string 5 + (2 + 3) • After lexical analysis (a list of tokens) int5 ‘+’ ‘(‘ int2 ‘+’ int3 ‘)’ • During parsing we build a parse tree … Compiler Design 1 (2011) 4 Example of Parse Tree E • Traces the operation of the parser E + E • Captures the nesting structure • But too much info int5 ( E ) – Parentheses – Single-successor nodes + E E int 2 int3 Compiler Design 1 (2011) 5 Example of Abstract Syntax Tree PLUS PLUS 5 2 3 • Also captures the nesting structure • But abstracts from the concrete syntax a more compact and easier to use • An important data structure in a compiler Compiler Design 1 (2011) 6 Semantic Actions • This is what we’ll use to construct ASTs • Each grammar symbol may have attributes – An attribute is a property of a programming language construct -

Compiler Construction
UNIVERSITY OF CAMBRIDGE Compiler Construction An 18-lecture course Alan Mycroft Computer Laboratory, Cambridge University http://www.cl.cam.ac.uk/users/am/ Lent Term 2007 Compiler Construction 1 Lent Term 2007 Course Plan UNIVERSITY OF CAMBRIDGE Part A : intro/background Part B : a simple compiler for a simple language Part C : implementing harder things Compiler Construction 2 Lent Term 2007 A compiler UNIVERSITY OF CAMBRIDGE A compiler is a program which translates the source form of a program into a semantically equivalent target form. • Traditionally this was machine code or relocatable binary form, but nowadays the target form may be a virtual machine (e.g. JVM) or indeed another language such as C. • Can appear a very hard program to write. • How can one even start? • It’s just like juggling too many balls (picking instructions while determining whether this ‘+’ is part of ‘++’ or whether its right operand is just a variable or an expression ...). Compiler Construction 3 Lent Term 2007 How to even start? UNIVERSITY OF CAMBRIDGE “When finding it hard to juggle 4 balls at once, juggle them each in turn instead ...” character -token -parse -intermediate -target stream stream tree code code syn trans cg lex A multi-pass compiler does one ‘simple’ thing at once and passes its output to the next stage. These are pretty standard stages, and indeed language and (e.g. JVM) system design has co-evolved around them. Compiler Construction 4 Lent Term 2007 Compilers can be big and hard to understand UNIVERSITY OF CAMBRIDGE Compilers can be very large. In 2004 the Gnu Compiler Collection (GCC) was noted to “[consist] of about 2.1 million lines of code and has been in development for over 15 years”. -

Advanced Parsing Techniques
Advanced Parsing Techniques Announcements ● Written Set 1 graded. ● Hard copies available for pickup right now. ● Electronic submissions: feedback returned later today. Where We Are Where We Are Parsing so Far ● We've explored five deterministic parsing algorithms: ● LL(1) ● LR(0) ● SLR(1) ● LALR(1) ● LR(1) ● These algorithms all have their limitations. ● Can we parse arbitrary context-free grammars? Why Parse Arbitrary Grammars? ● They're easier to write. ● Can leave operator precedence and associativity out of the grammar. ● No worries about shift/reduce or FIRST/FOLLOW conflicts. ● If ambiguous, can filter out invalid trees at the end. ● Generate candidate parse trees, then eliminate them when not needed. ● Practical concern for some languages. ● We need to have C and C++ compilers! Questions for Today ● How do you go about parsing ambiguous grammars efficiently? ● How do you produce all possible parse trees? ● What else can we do with a general parser? The Earley Parser Motivation: The Limits of LR ● LR parsers use shift and reduce actions to reduce the input to the start symbol. ● LR parsers cannot deterministically handle shift/reduce or reduce/reduce conflicts. ● However, they can nondeterministically handle these conflicts by guessing which option to choose. ● What if we try all options and see if any of them work? The Earley Parser ● Maintain a collection of Earley items, which are LR(0) items annotated with a start position. ● The item A → α·ω @n means we are working on recognizing A → αω, have seen α, and the start position of the item was the nth token. ● Using techniques similar to LR parsing, try to scan across the input creating these items. -

Lecture 3: Recursive Descent Limitations, Precedence Climbing
Lecture 3: Recursive descent limitations, precedence climbing David Hovemeyer September 9, 2020 601.428/628 Compilers and Interpreters Today I Limitations of recursive descent I Precedence climbing I Abstract syntax trees I Supporting parenthesized expressions Before we begin... Assume a context-free struct Node *Parser::parse_A() { grammar has the struct Node *next_tok = lexer_peek(m_lexer); following productions on if (!next_tok) { the nonterminal A: error("Unexpected end of input"); } A → b C A → d E struct Node *a = node_build0(NODE_A); int tag = node_get_tag(next_tok); (A, C, E are if (tag == TOK_b) { nonterminals; b, d are node_add_kid(a, expect(TOK_b)); node_add_kid(a, parse_C()); terminals) } else if (tag == TOK_d) { What is the problem node_add_kid(a, expect(TOK_d)); node_add_kid(a, parse_E()); with the parse function } shown on the right? return a; } Limitations of recursive descent Recall: a better infix expression grammar Grammar (start symbol is A): A → i = A T → T*F A → E T → T/F E → E + T T → F E → E-T F → i E → T F → n Precedence levels: Nonterminal Precedence Meaning Operators Associativity A lowest Assignment = right E Expression + - left T Term * / left F highest Factor No Parsing infix expressions Can we write a recursive descent parser for infix expressions using this grammar? Parsing infix expressions Can we write a recursive descent parser for infix expressions using this grammar? No Left recursion Left-associative operators want to have left-recursive productions, but recursive descent parsers can’t handle left recursion -
Top-Down Parsing & Bottom-Up Parsing I
Top-Down Parsing and Introduction to Bottom-Up Parsing Lecture 7 Instructor: Fredrik Kjolstad Slide design by Prof. Alex Aiken, with modifications 1 Predictive Parsers • Like recursive-descent but parser can “predict” which production to use – By looking at the next few tokens – No backtracking • Predictive parsers accept LL(k) grammars – L means “left-to-right” scan of input – L means “leftmost derivation” – k means “predict based on k tokens of lookahead” – In practice, LL(1) is used 2 LL(1) vs. Recursive Descent • In recursive-descent, – At each step, many choices of production to use – Backtracking used to undo bad choices • In LL(1), – At each step, only one choice of production – That is • When a non-terminal A is leftmost in a derivation • And the next input symbol is t • There is a unique production A ® a to use – Or no production to use (an error state) • LL(1) is a recursive descent variant without backtracking 3 Predictive Parsing and Left Factoring • Recall the grammar E ® T + E | T T ® int | int * T | ( E ) • Hard to predict because – For T two productions start with int – For E it is not clear how to predict • We need to left-factor the grammar 4 Left-Factoring Example • Recall the grammar E ® T + E | T T ® int | int * T | ( E ) • Factor out common prefixes of productions E ® T X X ® + E | e T ® int Y | ( E ) Y ® * T | e 5 LL(1) Parsing Table Example • Left-factored grammar E ® T X X ® + E | e T ® ( E ) | int Y Y ® * T | e • The LL(1) parsing table: next input token int * + ( ) $ E T X T X X + E e e T int Y ( E ) Y * T e e e rhs of production to use 6 leftmost non-terminal E ® T X X ® + E | e T ® ( E ) | int Y Y ® * T | e LL(1) Parsing Table Example • Consider the [E, int] entry – “When current non-terminal is E and next input is int, use production E ® T X” – This can generate an int in the first position int * + ( ) $ E T X T X X + E e e T int Y ( E ) Y * T e e e 7 E ® T X X ® + E | e T ® ( E ) | int Y Y ® * T | e LL(1) Parsing Tables. -

A Definite Clause Version of Categorial Grammar
A DEFINITE CLAUSE VERSION OF CATEGORIAL GRAMMAR Remo Pareschi," Department of Computer and Information Science, University of Pennsylvania, 200 S. 33 rd St., Philadelphia, PA 19104,t and Department of Artificial Intelligence and Centre for Cognitive Science, University of Edinburgh, 2 Buccleuch Place, Edinburgh EH8 9LW, Scotland remo(~linc.cis.upenn.edu ABSTRACT problem by adopting an intuitionistic treatment of implication, which has already been proposed We introduce a first-order version of Catego- elsewhere as an extension of Prolog for implement- rial Grammar, based on the idea of encoding syn- ing hypothetical reasoning and modular logic pro- tactic types as definite clauses. Thus, we drop gramming. all explicit requirements of adjacency between combinable constituents, and we capture word- order constraints simply by allowing subformu- 1 Introduction lae of complex types to share variables ranging over string positions. We are in this way able Classical Categorial Grammar (CG) [1] is an ap- to account for constructiods involving discontin- proach to natural language syntax where all lin- uous constituents. Such constructions axe difficult guistic information is encoded in the lexicon, via to handle in the more traditional version of Cate- the assignment of syntactic types to lexical items. gorial Grammar, which is based on propositional Such syntactic types can be viewed as expressions types and on the requirement of strict string ad- of an implicational calculus of propositions, where jacency between combinable constituents. atomic propositions correspond to atomic types, We show then how, for this formalism, parsing and implicational propositions account for com- can be efficiently implemented as theorem proving. plex types. -

Parse Trees (=Derivation Tree) by Constructing a Derivation
CFG: Parsing •Generative aspect of CFG: By now it should be clear how, from a CFG G, you can derive strings wÎL(G). CFG: Parsing •Analytical aspect: Given a CFG G and strings w, how do you decide if wÎL(G) and –if so– how do you determine the derivation tree or the sequence of production rules Recognition of strings in a that produce w? This is called the problem of parsing. language 1 2 CFG: Parsing CFG: Parsing • Parser A program that determines if a string w Î L(G) Parse trees (=Derivation Tree) by constructing a derivation. Equivalently, A parse tree is a graphical representation it searches the graph of G. of a derivation sequence of a sentential form. – Top-down parsers • Constructs the derivation tree from root to leaves. • Leftmost derivation. Tree nodes represent symbols of the – Bottom-up parsers grammar (nonterminals or terminals) and • Constructs the derivation tree from leaves to tree edges represent derivation steps. root. • Rightmost derivation in reverse. 3 4 CFG: Parsing CFG: Parsing Parse Tree: Example Parse Tree: Example 1 E ® E + E | E * E | ( E ) | - E | id Given the following grammar: Lets examine this derivation: E Þ -E Þ -(E) Þ -(E + E) Þ -(id + id) E ® E + E | E * E | ( E ) | - E | id E E E E E Is the string -(id + id) a sentence in this grammar? - E - E - E - E Yes because there is the following derivation: ( E ) ( E ) ( E ) E Þ -E Þ -(E) Þ -(E + E) Þ -(id + id) E + E E + E This is a top-down derivation because we start building the id id parse tree at the top parse tree 5 6 1 CFG: Parsing CFG: Parsing S ® SS | a | b Parse Tree: Example 2 Rightmost Parse Tree: Example 2 abÎ L( S) derivation S Þ SS Þ Sb Þ ab S S S S S S S S Derivation S S S S Derivation S S S S Trees S S Trees a a b S S b a b S S S Leftmost S derivation S Þ SS Þ aS Þ ab Rightmost Derivation a b S S in Reverse 7 8 CFG: Parsing CFG: Parsing Practical Parsers Example 3 Consider the CFG grammar G • Language/Grammar designed to enable deterministic (directed S ® A and backtrack-free) searches.