Quantifying CFSE Label Decay in Flow Cytometry Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Supplementary Table S4. FGA Co-Expressed Gene List in LUAD
Supplementary Table S4. FGA co-expressed gene list in LUAD tumors Symbol R Locus Description FGG 0.919 4q28 fibrinogen gamma chain FGL1 0.635 8p22 fibrinogen-like 1 SLC7A2 0.536 8p22 solute carrier family 7 (cationic amino acid transporter, y+ system), member 2 DUSP4 0.521 8p12-p11 dual specificity phosphatase 4 HAL 0.51 12q22-q24.1histidine ammonia-lyase PDE4D 0.499 5q12 phosphodiesterase 4D, cAMP-specific FURIN 0.497 15q26.1 furin (paired basic amino acid cleaving enzyme) CPS1 0.49 2q35 carbamoyl-phosphate synthase 1, mitochondrial TESC 0.478 12q24.22 tescalcin INHA 0.465 2q35 inhibin, alpha S100P 0.461 4p16 S100 calcium binding protein P VPS37A 0.447 8p22 vacuolar protein sorting 37 homolog A (S. cerevisiae) SLC16A14 0.447 2q36.3 solute carrier family 16, member 14 PPARGC1A 0.443 4p15.1 peroxisome proliferator-activated receptor gamma, coactivator 1 alpha SIK1 0.435 21q22.3 salt-inducible kinase 1 IRS2 0.434 13q34 insulin receptor substrate 2 RND1 0.433 12q12 Rho family GTPase 1 HGD 0.433 3q13.33 homogentisate 1,2-dioxygenase PTP4A1 0.432 6q12 protein tyrosine phosphatase type IVA, member 1 C8orf4 0.428 8p11.2 chromosome 8 open reading frame 4 DDC 0.427 7p12.2 dopa decarboxylase (aromatic L-amino acid decarboxylase) TACC2 0.427 10q26 transforming, acidic coiled-coil containing protein 2 MUC13 0.422 3q21.2 mucin 13, cell surface associated C5 0.412 9q33-q34 complement component 5 NR4A2 0.412 2q22-q23 nuclear receptor subfamily 4, group A, member 2 EYS 0.411 6q12 eyes shut homolog (Drosophila) GPX2 0.406 14q24.1 glutathione peroxidase -

The Metabolic Serine Hydrolases and Their Functions in Mammalian Physiology and Disease Jonathan Z
REVIEW pubs.acs.org/CR The Metabolic Serine Hydrolases and Their Functions in Mammalian Physiology and Disease Jonathan Z. Long* and Benjamin F. Cravatt* The Skaggs Institute for Chemical Biology and Department of Chemical Physiology, The Scripps Research Institute, 10550 North Torrey Pines Road, La Jolla, California 92037, United States CONTENTS 2.4. Other Phospholipases 6034 1. Introduction 6023 2.4.1. LIPG (Endothelial Lipase) 6034 2. Small-Molecule Hydrolases 6023 2.4.2. PLA1A (Phosphatidylserine-Specific 2.1. Intracellular Neutral Lipases 6023 PLA1) 6035 2.1.1. LIPE (Hormone-Sensitive Lipase) 6024 2.4.3. LIPH and LIPI (Phosphatidic Acid-Specific 2.1.2. PNPLA2 (Adipose Triglyceride Lipase) 6024 PLA1R and β) 6035 2.1.3. MGLL (Monoacylglycerol Lipase) 6025 2.4.4. PLB1 (Phospholipase B) 6035 2.1.4. DAGLA and DAGLB (Diacylglycerol Lipase 2.4.5. DDHD1 and DDHD2 (DDHD Domain R and β) 6026 Containing 1 and 2) 6035 2.1.5. CES3 (Carboxylesterase 3) 6026 2.4.6. ABHD4 (Alpha/Beta Hydrolase Domain 2.1.6. AADACL1 (Arylacetamide Deacetylase-like 1) 6026 Containing 4) 6036 2.1.7. ABHD6 (Alpha/Beta Hydrolase Domain 2.5. Small-Molecule Amidases 6036 Containing 6) 6027 2.5.1. FAAH and FAAH2 (Fatty Acid Amide 2.1.8. ABHD12 (Alpha/Beta Hydrolase Domain Hydrolase and FAAH2) 6036 Containing 12) 6027 2.5.2. AFMID (Arylformamidase) 6037 2.2. Extracellular Neutral Lipases 6027 2.6. Acyl-CoA Hydrolases 6037 2.2.1. PNLIP (Pancreatic Lipase) 6028 2.6.1. FASN (Fatty Acid Synthase) 6037 2.2.2. PNLIPRP1 and PNLIPR2 (Pancreatic 2.6.2. -

Thesis Rests with Its Author
University of Bath PHD An investigation of platelet-activating factor metabolism during normal and pre- eclamptic pregnancies Khan, Nighat Murad Award date: 1993 Awarding institution: University of Bath Link to publication Alternative formats If you require this document in an alternative format, please contact: [email protected] General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal ? Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Download date: 10. Oct. 2021 (i) A r c INVESTIGATION OF A 3sr o R METABOLISM DURING NORMAL AND PRE-ECLAMPTIC PREGNANCIES. Submitted by Nighat Murad Khan for the degree of Ph.D of the University of Bath 1992 Attention is drawn to the fact that copyright of this thesis rests with its author. This copy of the thesis has been supplied on the condition that anyone who consults it is understood to recognise that its copyright rests with its author and that no quotation from the thesis and no information derived from it may be published without written consent of the author. -
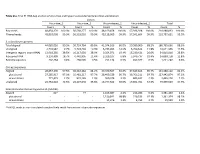
Table S1a. Trial #1 RNA-Seq Analysis of Virus-Free and Hypovirus
Table S1a. Trial #1 RNA-Seq analysis of virus-free and hypovirus-transfected Sclerotinia sclerotiorum Library Virus-free_1 Virus-free_2 Virus-infected_1 Virus-infected_2 Total Count % Count % Count % Count % Count % Raw reads 48,854,170 100.0% 56,568,277 100.0% 48,169,458 100.0% 57,396,928 100.0% 210,988,833 100.0% Filtered reads 48,810,008 99.9% 56,518,010 99.9% 48,118,009 99.9% 57,341,604 99.9% 210,787,631 99.9% S. sclerotiorum genome Total aligned 44,085,026 90.3% 50,724,764 89.8% 41,374,916 86.0% 50,580,960 88.2% 186,765,666 88.6% Unaligned 4,724,982 9.7% 5,793,246 10.3% 6,743,093 14.0% 6,760,644 11.8% 24,021,965 11.5% Intergenic regions (non-rRNA) 13,918,285 28.5% 16,317,039 28.9% 9,354,071 19.4% 15,230,421 26.6% 54,819,816 25.8% Ribosomal RNA 9,150,409 18.7% 6,442,905 11.4% 3,329,107 6.8% 5,976,737 10.4% 24,899,158 11.8% Retrotransposons 202,264 0.4% 268,505 0.5% 251,134 0.5% 499,377 0.9% 1,221,280 0.6% Coding sequences Aligned 28,057,390 57.5% 36,310,362 64.2% 29,370,507 61.0% 37,649,843 65.7% 131,388,102 62.1% plus strand 27,285,917 97.3% 35,481,217 97.7% 28,409,529 96.7% 36,766,211 97.7% 127,942,874 97.3% minus strand 771,473 2.7% 829,145 2.3% 960,978 3.3% 883,632 2.3% 3,445,228 2.7% Unaligned 20,752,618 42.5% 20,207,648 35.8% 18,747,502 39.0% 19,691,761 34.3% 79,399,529 37.9% Sclerotinia sclerotiorum hypovirus 2L (SsHV2L) Aligned 62* - 77 - 1,165,087 2.4% 216,286 0.4% 1,381,450 1.4% plus strand - - - - 1,150,841 98.8% 210,533 97.3% 1,361,374 98.1% minus strand - - - - 14,246 1.2% 5,753 2.7% 19,999 1.9% *SsHV2L reads in non-inoculated samples likely result from errors in barcode sequences. -

(12) United States Patent (10) Patent No.: US 8,561,811 B2 Bluchel Et Al
USOO8561811 B2 (12) United States Patent (10) Patent No.: US 8,561,811 B2 Bluchel et al. (45) Date of Patent: Oct. 22, 2013 (54) SUBSTRATE FOR IMMOBILIZING (56) References Cited FUNCTIONAL SUBSTANCES AND METHOD FOR PREPARING THE SAME U.S. PATENT DOCUMENTS 3,952,053 A 4, 1976 Brown, Jr. et al. (71) Applicants: Christian Gert Bluchel, Singapore 4.415,663 A 1 1/1983 Symon et al. (SG); Yanmei Wang, Singapore (SG) 4,576,928 A 3, 1986 Tani et al. 4.915,839 A 4, 1990 Marinaccio et al. (72) Inventors: Christian Gert Bluchel, Singapore 6,946,527 B2 9, 2005 Lemke et al. (SG); Yanmei Wang, Singapore (SG) FOREIGN PATENT DOCUMENTS (73) Assignee: Temasek Polytechnic, Singapore (SG) CN 101596422 A 12/2009 JP 2253813 A 10, 1990 (*) Notice: Subject to any disclaimer, the term of this JP 2258006 A 10, 1990 patent is extended or adjusted under 35 WO O2O2585 A2 1, 2002 U.S.C. 154(b) by 0 days. OTHER PUBLICATIONS (21) Appl. No.: 13/837,254 Inaternational Search Report for PCT/SG2011/000069 mailing date (22) Filed: Mar 15, 2013 of Apr. 12, 2011. Suen, Shing-Yi, et al. “Comparison of Ligand Density and Protein (65) Prior Publication Data Adsorption on Dye Affinity Membranes Using Difference Spacer Arms'. Separation Science and Technology, 35:1 (2000), pp. 69-87. US 2013/0210111A1 Aug. 15, 2013 Related U.S. Application Data Primary Examiner — Chester Barry (62) Division of application No. 13/580,055, filed as (74) Attorney, Agent, or Firm — Cantor Colburn LLP application No. -

Bioprospecting for Microorganisms and Enzymes with Biorefining Potential
Bioprospecting for Microorganisms and Enzymes with Biorefining Potential by Laura Frances Lyons Supervisors Dr Kerrie Farrar and Dr Justin Pachebat A thesis submitted at the Institute of Biological, Environmental and Rural Sciences (Aberystwyth University), for the degree of Doctor of Philosophy. 2015 1 2 Declaration This work has not previously been accepted in substance for any degree and is not being concurrently submitted in candidature for any degree. Signed ...................................................................... (candidate) Date ........................................................................ STATEMENT 1 This thesis is the result of my own investigations, except where otherwise stated. Where *correction services have been used, the extent and nature of the correction is clearly marked in a footnote(s). Other sources are acknowledged by footnotes giving explicit references. A bibliography is appended. Signed ..................................................................... (candidate) Date ........................................................................ [*this refers to the extent to which the text has been corrected by others] STATEMENT 2 I hereby give consent for my thesis, if accepted, to be available for photocopying and for inter-library loan, and for the title and summary to be made available to outside organisations. Signed ..................................................................... (candidate) Date ........................................................................ Word count -

Protein List
Protein Accession Protein Id Protein Name P11171 41 Protein 4. -

POLSKIE TOWARZYSTWO BIOCHEMICZNE Postępy Biochemii
POLSKIE TOWARZYSTWO BIOCHEMICZNE Postępy Biochemii http://rcin.org.pl WSKAZÓWKI DLA AUTORÓW Kwartalnik „Postępy Biochemii” publikuje artykuły monograficzne omawiające wąskie tematy, oraz artykuły przeglądowe referujące szersze zagadnienia z biochemii i nauk pokrewnych. Artykuły pierwszego typu winny w sposób syntetyczny omawiać wybrany temat na podstawie możliwie pełnego piśmiennictwa z kilku ostatnich lat, a artykuły drugiego typu na podstawie piśmiennictwa z ostatnich dwu lat. Objętość takich artykułów nie powinna przekraczać 25 stron maszynopisu (nie licząc ilustracji i piśmiennictwa). Kwartalnik publikuje także artykuły typu minireviews, do 10 stron maszynopisu, z dziedziny zainteresowań autora, opracowane na podstawie najnow szego piśmiennictwa, wystarczającego dla zilustrowania problemu. Ponadto kwartalnik publikuje krótkie noty, do 5 stron maszynopisu, informujące o nowych, interesujących osiągnięciach biochemii i nauk pokrewnych, oraz noty przybliżające historię badań w zakresie różnych dziedzin biochemii. Przekazanie artykułu do Redakcji jest równoznaczne z oświadczeniem, że nadesłana praca nie była i nie będzie publikowana w innym czasopiśmie, jeżeli zostanie ogłoszona w „Postępach Biochemii”. Autorzy artykułu odpowiadają za prawidłowość i ścisłość podanych informacji. Autorów obowiązuje korekta autorska. Koszty zmian tekstu w korekcie (poza poprawieniem błędów drukarskich) ponoszą autorzy. Artykuły honoruje się według obowiązujących stawek. Autorzy otrzymują bezpłatnie 25 odbitek swego artykułu; zamówienia na dodatkowe odbitki (płatne) należy zgłosić pisemnie odsyłając pracę po korekcie autorskiej. Redakcja prosi autorów o przestrzeganie następujących wskazówek: Forma maszynopisu: maszynopis pracy i wszelkie załączniki należy nadsyłać w dwu egzem plarzach. Maszynopis powinien być napisany jednostronnie, z podwójną interlinią, z marginesem ok. 4 cm po lewej i ok. 1 cm po prawej stronie; nie może zawierać więcej niż 60 znaków w jednym wierszu nie więcej niż 30 wierszy na stronie zgodnie z Normą Polską. -

Developmental Acquisition of the Lyn-CD22-SHP-1 Inhibitory Pathway Promotes B Cell Tolerance
Developmental Acquisition of the Lyn-CD22-SHP-1 Inhibitory Pathway Promotes B Cell Tolerance This information is current as Andrew J. Gross, Julia R. Lyandres, Anil K. Panigrahi, Eline of October 1, 2021. T. Luning Prak and Anthony L. DeFranco J Immunol 2009; 182:5382-5392; ; doi: 10.4049/jimmunol.0803941 http://www.jimmunol.org/content/182/9/5382 Downloaded from Supplementary http://www.jimmunol.org/content/suppl/2009/04/20/182.9.5382.DC1 Material References This article cites 48 articles, 26 of which you can access for free at: http://www.jimmunol.org/ http://www.jimmunol.org/content/182/9/5382.full#ref-list-1 Why The JI? Submit online. • Rapid Reviews! 30 days* from submission to initial decision • No Triage! Every submission reviewed by practicing scientists by guest on October 1, 2021 • Fast Publication! 4 weeks from acceptance to publication *average Subscription Information about subscribing to The Journal of Immunology is online at: http://jimmunol.org/subscription Permissions Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Email Alerts Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts The Journal of Immunology is published twice each month by The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2009 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. The Journal of Immunology Developmental Acquisition of the Lyn-CD22-SHP-1 Inhibitory Pathway Promotes B Cell Tolerance1 Andrew J. Gross,* Julia R. -

Lack of Association Between Rare Mutations of the SIAE Gene and Rheumatoid Arthritis in a Han Chinese Population
Lack of association between rare mutations of the SIAE gene and rheumatoid arthritis in a Han Chinese population D.D. Zhang1,2*, F. He3*, H.T. Liu4*, F. Hao1 and J. Zhu5 1Sichuan Key Laboratory for Disease Gene Study, Sichuan Academy of Medical Sciences and Sichuan Provincial People’s Hospital, Sichuan, China 2Department of Health Management, Sichuan Academy of Medical Sciences and Sichuan Provincial People’s Hospital, Sichuan, China 3School of Life Science and Biotechnology, Mianyang Normal University, Sichuan, China 4Guangya School, Guangdong, China 5Department of Rheumatology and Immunology, Sichuan Academy of Medical Sciences and Sichuan Provincial People’s Hospital, Chengdu, Sichuan, China *These authors contributed equally to the study. Corresponding author: D.D. Zhang E-mail: [email protected] Genet. Mol. Res. 14 (4): 14162-14168 (2015) Received July 16, 2015 Accepted September 29, 2015 Published October 29, 2015 DOI http://dx.doi.org/10.4238/2015.October.29.38 ABSTRACT. The function of rare genotypes encoding defective variants of sialic acid acetylesterase (SIAE) in some autoimmune diseases, including rheumatoid arthritis (RA), is ambiguous. We determined whether mutations in the SIAE gene are responsible for RA in a Han Chinese population. DNA was prepared from the venous leukocytes of 444 RA patients and 647 normal controls. The coding regions and adjacent intron sequences of SIAE were amplified by polymerase chain reaction. The products were Genetics and Molecular Research 14 (4): 14162-14168 (2015) ©FUNPEC-RP www.funpecrp.com.br Mutations of the SIAE gene and rheumatoid arthritis 14163 then subjected to sequencing analysis. The detected variations were further evaluated in the normal controls and available family members by sequencing. -

Boophilus Microplus: Characterization of Enzymes Introduced Into the Host
Aust. J. Bioi. Sci., 1976, 29, 487-97 Boophilus microplus: Characterization of Enzymes Introduced into the Host A. V. Schleger and D. T. Lincoln Division of Animal Production, CSIRO, Long Pocket Laboratories, Private Bag No.3, Indooroopilly, Qld 4068. Abstract A number of enzymes, presumably secreted by larvae of B. microplus under natural feeding conditions, have been investigated in the skin of previously unexposed calves 4 h after infestation at the attachment site. Carboxylic ester hydrolase activity was demonstrated in the dermis, immediately adjacent to the mouthparts, or in the attachment cone, depending on substrate and reaction pH. The carboxylic ester hydrolase acting on naphthol AS-D acetate (2-acetoxy-3-naphthoic-O-toluidide) at pH 7·1 was characteristically found in the dermis and not in the attachment cone. The use of specific inhibitors showed that this enzyme was primarily a B-esterase or carboxylesterase with possibly a small portion of C-esterase or acetylesterase. It is postulated that carboxylic ester hydrolase could contribute to the dilation observed in the subepidermal capillaries adjacent to the attachment sites of unexposed animals, through the formation of plasma kinins. Other enzymes demonstrated in the dermis, adjacent to the mouthparts, were triacylglycerol lipase, as an aggregated deposit, and small amounts of aminopeptidase (microsomal) and monophenol monooxygenase. Aminopeptidase (microsomal) was also demonstrated in the attachment cone or adjacent epidermis, according to the substrate used. No activity was found in the host tissue, in association with the attachment site, for either alkaline or acid phosphatase, acetylcholinesterase or cholinesterase, peroxidase or amine oxidase (flavin-containing), despite the intense histochemical reaction for the latter in the tissues of larvae. -

Carboxylic Ester Hydrolases in Bacteria: Active Site, Structure, Function and Application
crystals Review Carboxylic Ester Hydrolases in Bacteria: Active Site, Structure, Function and Application Changsuk Oh 1 , T. Doohun Kim 2,* and Kyeong Kyu Kim 1,* 1 Department of Molecular Cell Biology, Sungkyunkwan University School of Medicine, Suwon 16419, Korea; [email protected] 2 Department of Chemistry, College of Natural Science, Sookmyung Women’s University, Seoul 04310, Korea * Correspondence: [email protected] (T.D.K.); [email protected] (K.K.K.) Received: 4 October 2019; Accepted: 7 November 2019; Published: 14 November 2019 Abstract: Carboxylic ester hydrolases (CEHs), which catalyze the hydrolysis of carboxylic esters to produce alcohol and acid, are identified in three domains of life. In the Protein Data Bank (PDB), 136 crystal structures of bacterial CEHs (424 PDB codes) from 52 genera and metagenome have been reported. In this review, we categorize these structures based on catalytic machinery, structure and substrate specificity to provide a comprehensive understanding of the bacterial CEHs. CEHs use Ser, Asp or water as a nucleophile to drive diverse catalytic machinery. The α/β/α sandwich architecture is most frequently found in CEHs, but 3-solenoid, β-barrel, up-down bundle, α/β/β/α 4-layer sandwich, 6 or 7 propeller and α/β barrel architectures are also found in these CEHs. Most are substrate-specific to various esters with types of head group and lengths of the acyl chain, but some CEHs exhibit peptidase or lactamase activities. CEHs are widely used in industrial applications, and are the objects of research in structure- or mutation-based protein engineering. Structural studies of CEHs are still necessary for understanding their biological roles, identifying their structure-based functions and structure-based engineering and their potential industrial applications.