A General Framework for Portfolio Theory. Part I: Theory and Various Models
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Capital Asset Pricing Model (Capm)
THE CAPITAL ASSET PRICING MODEL (CAPM) Investment and Valuation of Firms Juan Jose Garcia Machado WS 2012/2013 November 12, 2012 Fanck Leonard Basiliki Loli Blaž Kralj Vasileios Vlachos Contents 1. CAPM............................................................................................................................................... 3 2. Risk and return trade off ............................................................................................................... 4 Risk ................................................................................................................................................... 4 Correlation....................................................................................................................................... 5 Assumptions Underlying the CAPM ............................................................................................. 5 3. Market portfolio .............................................................................................................................. 5 Portfolio Choice in the CAPM World ........................................................................................... 7 4. CAPITAL MARKET LINE ........................................................................................................... 7 Sharpe ratio & Alpha ................................................................................................................... 10 5. SECURITY MARKET LINE ................................................................................................... -

Empirical Study on CAPM Model on China Stock Market
Empirical study on CAPM model on China stock market MASTER THESIS WITHIN: Business administration in finance NUMBER OF CREDITS: 15 ECTS TUTOR: Andreas Stephan PROGRAMME OF STUDY: international financial analysis AUTHOR: Taoyuan Zhou, Huarong Liu JÖNKÖPING 05/2018 Master Thesis in Business Administration Title: Empirical study on CAPM model of China stock market Authors: Taoyuan Zhou and Huarong Liu Tutor: Andreas Stephan Date: 05/2018 Key terms: CAPM model, β coefficient, empirical test Abstract Background: The capital asset pricing model (CAPM) describes the interrelationship between the expected return of risk assets and risk in the equilibrium of investment market and gives the equilibrium price of risky assets (Banz, 1981). CAPM plays a very important role in the process of establishing a portfolio (Bodie, 2009). As Chinese stock market continues to grow and expand, the scope and degree of attention of CAPM models in China will also increase day by day. Therefore, in China, such an emerging market, it is greatly necessary to test the applicability and validity of the CAPM model in the capital market. Purpose: Through the monthly data of 100 stocks from January 1, 2007 to February 1, 2018, the time series and cross-sectional data of the capital asset pricing model on Chinese stock market are tested. The main objectives are: (1) Empirical study of the relationship between risk and return using the data of Chinese stock market in recent years to test whether the CAPM model established in the developed western market is suitable for the Chinese market. (2) Through the empirical analysis of the results to analyse the characteristics and existing problems of Chinese capital market. -

2. Capital Asset Pricing Model
2. Capital Asset pricing Model Dr. Youchang Wu WS 2007 Asset Management Youchang Wu 1 Efficient frontier in the presence of a risk-free asset Asset Management Youchang Wu 2 Capital market line When a risk-free asset exists, i. e., when a capital market is introduced, the efficient frontier is linear. This linear frontier is called capital market line The capital market line touches the efficient frontier of the risky assets only at the tangency portfolio The optimal portfolio of any investor with mean-variance preference can be constructed using the risk-free asset and the tangency portfolio, which contains only risky assets (Two-fund separation ) All investors with a mean-variance preference, independent of their risk attitudes, hold the same portfolio of risky assets. The risk attitude only affects the relative weights of the risk-free asset and the risky portfolio Asset Management Youchang Wu 3 Market price of risk The equation for the capital market line E(rT ) − rf E(rP ) = rf + σ (rp ) σ (rT ) The slope of the capital market line represents the best risk-return tdtrade-off tha t i s ava ilabl e on the mar ke t Without the risk-free asset, the marginal rate of substitution between risk and return will be different across investors After i nt rod uci ng the r is k-free asse t, it will be the same for a ll investors. Almost all investors benefit from introducing the risk-free asset (capital market) Reminiscent of the Fisher Separation Theorem? Asset Management Youchang Wu 4 Remaining questions What would be the tangency portfolio in equilibrium? CML describes the risk-return relation for all efficient portfolios, but what is the equilibrium relation between risk and return for inefficient portfolios or individual assets? What if the risk-free asset does not exist? Asset Management Youchang Wu 5 CAPM If everyb bdody h hldholds the same ri iksky portf fliolio, t hen t he r ikisky port flifolio must be the MARKET portfolio, i.e., the value-weighted portfolio of all securities (demand must equal supply in equilibrium!). -

The Economics of Financial Markets
The Economics of Financial Markets Roy E. Bailey Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo Cambridge University Press The Edinburgh Building, Cambridge ,UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridg e.org /9780521848275 © R. E. Bailey 2005 This book is in copyright. Subject to statutory exception and to the provision of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published in print format 2005 - ---- eBook (EBL) - --- eBook (EBL) - ---- hardback - --- hardback - ---- paperback - --- paperback Cambridge University Press has no responsibility for the persistence or accuracy of s for external or third-party internet websites referred to in this book, and does not guarantee that any content on such websites is, or will remain, accurate or appropriate. The Theory of Economics does not furnish a body of settled conclusions imme- diately applicable to policy. It is a method rather than a doctrine, an apparatus of the mind, a technique of thinking, which helps its possessor to draw correct conclusions. It is not difficult in the sense in which mathematical and scientific techniques are difficult; but the fact that its modes of expression are much less precise than these, renders decidedly difficult the task of conveying it correctly to the minds of learners. J. M. Keynes When you set out for distant Ithaca, -

Markowitz Efficient Frontier and Capital Market Line – Evidence from the Portuguese Stock Market
MARKOWITZ EFFICIENT FRONTIER AND CAPITAL MARKET LINE – EVIDENCE FROM THE PORTUGUESE STOCK MARKET 1 2 The European Journal of Management Teresa Garcia and Daniel Borrego Studies is a publication of ISEG, 1 Universidade de Lisboa. The mission of ISEG – Lisbon School of Economics and EJMS is to significantly influence the domain of management studies by Management, Universidade de Lisboa, and UECE, publishing innovative research articles. Portugal; 2ISEG – Lisbon School of Economics and EJMS aspires to provide a platform for Management, Universidade de Lisboa thought leadership and outreach. Editors-in-Chief: Luís M. de Castro, PhD ISEG - Lisbon School of Economics and Management, Universidade de Lisboa, Abstract Portugal Gurpreet Dhillon, PhD This paper estimates the efficient frontier and the capital Virginia Commonwealth University, USA market line using listed stocks of the Portuguese capital Tiago Cardão-Pito, PhD ISEG - Lisbon School of Economics and market that are part of the PSI20 index, considering two Management, Universidade de Lisboa, different periods - before and after the 2008 financial crisis, Portugal known as the Global Financial Crisis. The results show the Managing Editor: impact of the 2008 financial crisis on the global minimum Mark Crathorne, MA ISEG - Lisbon School of Economics and variance portfolio and on the market portfolio. The sensitivity Management, Universidade de Lisboa, analysis of the results to the inclusion or not of the year 2008 Portugal is also considered1. ISSN: 2183-4172 Volume 22, Issue 1 www.european-jms.com Key words: Markowitz portfolio theory. Mean-variance theory. Efficient Frontier. Capital Market Line. PSI20. 1 The authors would like to acknowledge the financial support received from FCT (Fundação para a Ciência e a Tecnologia), Portugal. -

Appendix 1: Transaction Costs
Appendix 1: transaction costs Commission Commission is charged on purchases and sales of government and corporate securities and of financial futures and options. There are no minimum commissions: rates are negotiable between the client and the broker, with the average size of the transactions and the frequency of trading being taken into consideration. Commission are expressed as a percentage of the value of the transaction and do not currently attract Value Added Tax. Typical commissions on ordinary share purchases and sales are 1 %-l.S% for transactions of below £5,000 in value falling to O.S% for transactions of over £10,000 and 0.2% for institutional-size trades. Typical commissions on gilt purchases and sales are O.S%-1% for transactions of below £5,000 falling to 0.2% for over £20,000 and no commissions are payable for transactions in excess of £1,000,000 in value. Notice that the gilts can be purchased from the National Savings Stock Register via the post office. Transaction costs here are fixed at SOp per £125 in value (with a £1 minimum) for purchases and sales. Typical commissions on futures and options transactions might be 2.S% for purchases worth up to £5,000 with no commission being charged on sales. How ever, for larger value transactions, commissions would be quoted as an amount in pounds per contract, typically £10-£20 for both a purchase and sale, known as a 'round trip', depending on the particular contract. Stamp duty Transfer stamp duty is payable by the purchaser of UK-registered securities (whether or not listed on the Stock Exchange) which require completion of a transfer form. -

Portfolio Theory & Financial Analyses: Exercises
Robert Alan Hill Portfolio Theory & Financial Analyses: Exercises Download free ebooks at bookboon.com 2 Portfolio Theory & Financial Analyses: Exercises © 2010 Robert Alan Hill & Ventus Publishing ApS ISBN 978-87-7681-616-2 Download free ebooks at bookboon.com 3 Portfolio Theory & Financial Analyses: Exercises Contents Contents Part I: An Introduction 7 1. An Overview 7 Introduction 7 Exercise 1.1: The Mean-Variance Paradox 8 Exercise 1.2: The Concept of Investor Utility 10 Summary and Conclusions 10 Selected References (From PTFA) 11 Part II: The Portfolio Decision 13 2. Risk and Portfolio Analysis 13 Introduction 13 Exercise 2.1: A Guide to Further Study 13 Exercise 2.2: The Correlation Coefficient and Risk 14 Exercise 2.3: Correlation and Risk Reduction 16 Summary and Conclusions 18 Selected References 19 3. The Optimum Portfolio 20 Introduction 20 Exercise 3.1: Two-Asset Portfolio Risk Minimisation 21 Exercise 3.2: Two-Asset Portfolio Minimum Variance (I) 24 e Graduate Programme I joined MITAS because for Engineers and Geoscientists I wanted real responsibili Maersk.com/Mitas Month 16 I wwasas a construction supervisor in Please click the advert the North Sea advising and Real work hhelpinge foremen InternationalInternationaal opportunities reeree workworo placements ssolve problems Download free ebooks at bookboon.com 4 Portfolio Theory & Financial Analyses: Exercises Contents Exercise 3.3: Two-Asset Portfolio Minimum Variance (II) 27 Exercise 3.4: The Multi-Asset Portfolio 29 Summary and Conclusions 30 Selected References 30 4. The Market Portfolio 31 Introduction 31 Exercise 4.1: Tobin and Perfect Capital Markets 32 Exercise 4.2: The Market Portfolio and Tobin’s Theorem 34 Summary and Conclusions 39 Selected References 40 Part III: Models of Capital Asset Pricing 41 5. -

Elements of Financial Engineering Course
Baruch-NSD_Summer2019-Lec4-ModernPortfolioTheory http://localhost:8888/nbconvert/html/Google Drive/Lectures/Ba... Elements of Financial Engineering Course Baruch-NSD Summer Camp 2019 Lecture 4: Modern Portfolio Theory and CAPM Tai-Ho Wang (王 太 和) Outline of the lecture Modern portfolio theory and the Markowitz model Capital asset pricing model (CAPM) Arbitrage pricing theory (APT) Fama-French 3-factor model Black-Litterman model Merton's problem Harry Markowitz From the Wikipage (https://en.wikipedia.org/wiki/Harry_Markowitz) in Wikipedia: Markowitz won the Nobel Memorial Prize in Economic Sciences in 1990 while a professor of finance at Baruch College of the City University of New York. In the preceding year, he received the John von Neumann Theory Prize from the Operations Research Society of America (now Institute for Operations Research and the Management Sciences, INFORMS) for his contributions in the theory of three fields: portfolio theory; sparse matrix methods; and simulation language programming (SIMSCRIPT). Extensions From Wikipedia: Since MPT's introduction in 1952, many attempts have been made to improve the model, especially by using more realistic assumptions. Post-modern portfolio theory extends MPT by adopting non-normally distributed, asymmetric, and fat-tailed measures of risk. This helps with some of these problems, but not others. Black-Litterman model optimization is an extension of unconstrained Markowitz optimization that incorporates relative and absolute 'views' on inputs of risk and returns from financial experts. With the advances in Artificial Intelligence, other information such as market sentiment and financial knowledge can be incorporated automatically to the 'views'. 1 of 31 8/13/19, 8:21 PM Baruch-NSD_Summer2019-Lec4-ModernPortfolioTheory http://localhost:8888/nbconvert/html/Google Drive/Lectures/Ba.. -
![[Roy E. Bailey] the Economics of Financial Markets](https://docslib.b-cdn.net/cover/5964/roy-e-bailey-the-economics-of-financial-markets-3445964.webp)
[Roy E. Bailey] the Economics of Financial Markets
The Economics of Financial Markets Roy E. Bailey Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo Cambridge University Press The Edinburgh Building, Cambridge ,UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambrig e.org /9780521848275d © R. E. Bailey 2005 This book is in copyright. Subject to statutory exception and to the provision of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published in print format 2005 - ---- eBook (EBL) - --- eBook (EBL) - ---- hardback - --- hardback - ---- paperback - --- paperback Cambridge University Press has no responsibility for the persistence or accuracy of s for external or third-party internet websites referred to in this book, and does not guarantee that any content on such websites is, or will remain, accurate or appropriate. Contents List of figures page xv Preface xvii 1 Asset markets and asset prices 1 1.1 Capital markets 2 1.2 Asset price determination: an introduction 5 1.3 The role of expectations 9 1.4 Performance risk, margins and short-selling 11 1.5 Arbitrage 15 1.6 The role of time 20 1.7 Asset market efficiency 22 1.8 Summary 23 Appendix 1.1: Averages and indexes of stock prices 24 Appendix 1.2: Real rates of return 28 Appendix 1.3: Continuous compounding and the force of interest 29 References 32 2 Asset market microstructure 33 2.1 Financial markets: functions and -

A General Framework for Portfolio Theory—Part I: Theory and Various Models
risks Article A General Framework for Portfolio Theory—Part I: Theory and Various Models Stanislaus Maier-Paape 1,* and Qiji Jim Zhu 2 1 Institut für Mathematik, RWTH Aachen University, Templergraben 55, 52062 Aachen, Germany 2 Department of Mathematics, Western Michigan University, 1903 West Michigan Avenue, Kalamazoo, MI 49008, USA; [email protected] * Correspondence: [email protected]; Tel.: +49-(0)241-8094925 Received: 30 March 2018; Accepted: 1 May 2018; Published: 8 May 2018 Abstract: Utility and risk are two often competing measurements on the investment success. We show that efficient trade-off between these two measurements for investment portfolios happens, in general, on a convex curve in the two-dimensional space of utility and risk. This is a rather general pattern. The modern portfolio theory of Markowitz (1959) and the capital market pricing model Sharpe (1964), are special cases of our general framework when the risk measure is taken to be the standard deviation and the utility function is the identity mapping. Using our general framework, we also recover and extend the results in Rockafellar et al. (2006), which were already an extension of the capital market pricing model to allow for the use of more general deviation measures. This generalized capital asset pricing model also applies to e.g., when an approximation of the maximum drawdown is considered as a risk measure. Furthermore, the consideration of a general utility function allows for going beyond the “additive” performance measure to a “multiplicative” one of cumulative returns by using the log utility. As a result, the growth optimal portfolio theory Lintner (1965) and the leverage space portfolio theory Vince (2009) can also be understood and enhanced under our general framework. -
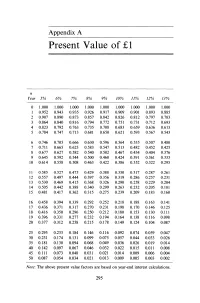
Present Value of £1
Appendix A Present Value of £1 n Year 5% 6% 7% 8% 9% 10% 11% 12% 13% 0 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1 0.952 0.943 0.935 0.926 0.917 0.909 0.901 0.893 0.885 2 0.907 0.890 0.873 0.857 0.842 0.826 0.812 0.797 0.783 3 0.864 0.840 0.816 0.794 0.772 0.751 0.731 0.712 0.693 4 0.823 0.792 0.763 0.735 0.708 0.683 0.659 0.636 0.613 5 0.784 0.747 0.713 0.681 0.650 0.621 0.593 0.567 0.543 6 0.746 0.705 0.666 0.630 0.596 0.564 0.535 0.507 0.480 7 0.711 0.665 0.623 0.583 0.547 0.513 0.482 0.452 0.425 8 0.677 0.627 0.582 0.540 0.502 0.467 0.434 0.404 0.376 9 0.645 0.592 0.544 0.500 0.460 0.424 0.391 0.361 0.333 10 0.614 0.558 0.508 0.463 0.422 0.386 0.352 0.322 0.295 11 0.585 0.527 0.475 0.429 0.388 0.350 0.317 0.287 0.261 12 0.557 0.497 0.444 0.397 0.356 0.319 0.286 0.257 0.231 13 0.530 0.469 0.415 0.368 0.326 0.290 0.258 0.229 0.204 14 0.505 0.442 0.388 0.340 0.299 0.263 0.232 0.205 0.181 15 0.481 0.417 0.362 0.315 0.275 0.239 0.209 0.183 0.160 16 0.458 0.394 0.339 0.292 0.252 0.218 0.188 0.163 0.141 17 0.436 0.371 0.317 0.270 0.231 0.198 0.170 0.146 0.125 18 0.416 0.350 0.296 0.250 0.212 0.180 0.153 0.130 0.111 19 0.396 0.331 0.277 0.232 0.194 0.164 0.138 0.116 0.098 20 0.377 0.312 0.258 0.215 0.178 0.149 0.124 0.104 0.087 25 0.295 0.233 0.184 0.146 0.116 0.092 0.074 0.059 0.047 30 0.231 0.174 0.131 0.099 0.075 0.057 0.044 0.033 0.026 35 0.181 0.130 0.094 0.068 0.049 0.036 0.026 0.019 0.014 40 0.142 0.097 0.067 0.046 0.032 0.022 0.015 0.011 0.008 45 0.111 0.073 0.048 0.031 0.021 0.014 0.009 0.006 0.004 50 0.087 0.054 0.034 0.021 0.013 0.009 0.005 0.003 0.002 Note: The above present value factors are based on year-end interest calculations. -

Capital Asset Pricing Model Homework Problems
Capital Asset Pricing Model Homework Problems Portfolio weights and expected return 1. Consider a portfolio of 300 shares of firm A worth $10/share and 50 shares of firm B worth $40/share. You expect a return of 8% for stock A and a return of 13% for stock B. (a) What is the total value of the portfolio, what are the portfolio weights and what is the expected return? (b) Suppose firm A's share price goes up to $12 and firm B's share price falls to $36. What is the new value of the portfolio? What return did it earn? After the price change, what are the new portfolio weights? 2. Consider a portfolio of 250 shares of firm A worth $30/share and 1500 shares of firm B worth $20/share. You expect a return of 4% for stock A and a return of 9% for stock B. (a) What is the total value of the portfolio, what are the portfolio weights and what is the expected return? (b) Suppose firm A's share price falls to $24 and firm B's share price goes up to $22. What is the new value of the portfolio? What return did it earn? After the price change, what are the new portfolio weights? Portfolio volatility 3. For the following problem please refer to Table 1 (Table 11.3, p. 336 in Corporate Finance by Berk and DeMarzo). (a) What is the covariance between the returns for Alaskan Air and General Mills? (b) What is the volatility of a portfolio with i.