Observations and Modeling of Typhoon Waves in the South China Sea
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Typhoon Hagupit (Ruby), Dec
Typhoon Hagupit (Ruby), Dec. 9, 2014 CDIR No. 6 BLUF – Implications to PACOM No DOD requirements anticipated PACOM Joint Liaison Group re-deploying from Philippines within next 72 hours (PACOM J35) Typhoon Hagupit – Stats & Facts Summary: (The following times in this report are Phil. local time unless otherwise specified) Current Status: Typhoon Hagupit has weakened into a tropical depression as it heads west into the West Philippine Sea towards Vietnam. All public storm warning signals have been lifted. Storm expected to head out of the Philippine Area of Responsibility (PAR) Thursday (11 DEC) early AM. Est. rainfall is 5 – 15 mm per hour (Moderate – heavy) within the 200 km of the storm. (NDRRMC, Bulletin No. 23) Local officials reported nearly 13,000 houses were destroyed and more than 22,300 were partially damaged in Eastern Samar province, where Hagupit first hit as a CAT 3 typhoon on 6 DEC. (Reuters) Deputy Presidential Spokesperson Key Concerns & Trends Abigail Valte said so far, Dolores appears worst hit. (GPH) Domestic air and sea travel has resumed, markets reopened • GPH and the international humanitarian community are and state workers returned to their offices. Some shopping capable of meeting virtually all disaster response requirements. Major malls were open but schools remained closed. actions and activities include: The privately run National Grid Corp said nearly two million Assessments are ongoing to determine the full extent of the homes across central Philippines and southern Luzon remain typhoon’s impact; reports so far indicate the scale and severity without power. (Reuters) Twenty provinces in six regions of the impact of Hagupit was not as great as initially feared. -
Appendix 8: Damages Caused by Natural Disasters
Building Disaster and Climate Resilient Cities in ASEAN Draft Finnal Report APPENDIX 8: DAMAGES CAUSED BY NATURAL DISASTERS A8.1 Flood & Typhoon Table A8.1.1 Record of Flood & Typhoon (Cambodia) Place Date Damage Cambodia Flood Aug 1999 The flash floods, triggered by torrential rains during the first week of August, caused significant damage in the provinces of Sihanoukville, Koh Kong and Kam Pot. As of 10 August, four people were killed, some 8,000 people were left homeless, and 200 meters of railroads were washed away. More than 12,000 hectares of rice paddies were flooded in Kam Pot province alone. Floods Nov 1999 Continued torrential rains during October and early November caused flash floods and affected five southern provinces: Takeo, Kandal, Kampong Speu, Phnom Penh Municipality and Pursat. The report indicates that the floods affected 21,334 families and around 9,900 ha of rice field. IFRC's situation report dated 9 November stated that 3,561 houses are damaged/destroyed. So far, there has been no report of casualties. Flood Aug 2000 The second floods has caused serious damages on provinces in the North, the East and the South, especially in Takeo Province. Three provinces along Mekong River (Stung Treng, Kratie and Kompong Cham) and Municipality of Phnom Penh have declared the state of emergency. 121,000 families have been affected, more than 170 people were killed, and some $10 million in rice crops has been destroyed. Immediate needs include food, shelter, and the repair or replacement of homes, household items, and sanitation facilities as water levels in the Delta continue to fall. -

Member Report (Malaysia)
MEMBER REPORT (MALAYSIA) ESCAP/WMO Typhoon Committee 15th Integrated Workshop Video Conference 1-2 December 2020 Organised by Viet Nam Table of Contents I. Overview of tropical cyclones which have affected/impacted Malaysia in 2020 1. Meteorological Assessment (highlighting forecasting issues/impacts) 2. Hydrological Assessment (highlighting water-related issues/impact) (a) Flash flood in Kajang & Kuala Lumpur in July and September 2020 (b) Enhancement of Hydrological Data Management for DID Malaysia (c) Hydrological Instrumentation Updates for Malaysia (d) Drought Monitoring Updates 3. Socio-Economic Assessment (highlighting socio-economic and DRR issues/impacts) 4. Regional Cooperation Assessment (highlighting regional cooperation successes and challenges) II. Summary of progress in Priorities supporting Key Result Areas 1. Annual Operating Plan (AOP) for Working Group of Meteorology [AOP4: Radar Integrated Nowcasting System (RaINS)] 2. Annual Operating Plan (AOP) for Working Group of Hydrology (AOP2, AOP4, AOP5, AOP6) 3. The Government of Malaysia’s Commitment Towards Supporting the Sendai Framework for Disaster Risk Reduction I. Overview of tropical cyclones which have affected/impacted Malaysia in 2020 1. Meteorological Assessment (highlighting forecasting issues/impacts) During the period of 1 November 2019 to 31 October 2020, 27 tropical cyclones (TCs) formed over the Western Pacific Ocean, the Philippines waters as well as the South China Sea. Eight of the TCs entered the area of responsibility of the Malaysian Meteorological Department (MET Malaysia) as shown in Figure 1. The TCs, which consisted of seven typhoons and a tropical storm that required the issuance of strong winds and rough seas warnings over the marine regions under the responsibility of MET Malaysia, are listed in Table 1. -

TUESDAY 16* Philippines 3,479* 1,167*
TUESDAY TYPHOON KALMAEGI 19 NOV 2019 PHILIPPINES 1230 HRS (UTC +7) FLASH UPDATE #2 Population Exposed (Estimated exposure by the PDC) Map source: Philippines Atmospheric, Geophysical and Astronomical Services Administration (PAGASA) Initial Effects* *Estimations are based on data reported/confirmed by National Disaster 3,479* 1,167* 15* 16* Management Organisations of each AFFECTED DISPLACED FLOODED DAMAGED respective ASEAN Member State PERSONS PERSONS BARANGAYS HOUSES and other verified sources Philippines • Tropical Storm KALMAEGI (locally named RAMON in the Philippines), which strengthened into a Severe Tropical Storm on 18 November 2019, has now further developed into a Typhoon and currently moving slowly west-northwest towards Babuyan Islands, north of Luzon, Philippines as of 10:00 (UTC+7). • According to forecast by the Joint Typhoon Warning Center (JTWC), Typhoon KALMAEGI is moving at about 4 kph, and is expected to weaken over the next 24 hours. Based on the current forecast (the storm's center and path), the Typhoon is within 112 km from northern seaboard of the Philippines, and the center is expected to make landfall in the afternoon or evening today, 19 November 2019, with sustained winds of about 148 kph. • The Philippines Atmospheric, Geophysical and Astronomical Services Administration (PAGASA) stated that moderate with frequent heavy rains will prevail over Batanes, northern portion of Cagayan (including the Babuyan Islands), Apayao and the northern portion of Ilocos Norte provinces. • The Philippines’ National Disaster Risk Reduction Management Council (NDRRMC) reported flood incidents, ranging from 0.5m to 1m of flood water, in 15 barangays/villages in Camarines Sur and Romblon provinces due to persistent heavy rains associated with the typhoon. -

Report on UN ESCAP / WMO Typhoon Committee Members Disaster Management System
Report on UN ESCAP / WMO Typhoon Committee Members Disaster Management System UNITED NATIONS Economic and Social Commission for Asia and the Pacific January 2009 Disaster Management ˆ ` 2009.1.29 4:39 PM ˘ ` 1 ¿ ‚fiˆ •´ lp125 1200DPI 133LPI Report on UN ESCAP/WMO Typhoon Committee Members Disaster Management System By National Institute for Disaster Prevention (NIDP) January 2009, 154 pages Author : Dr. Waonho Yi Dr. Tae Sung Cheong Mr. Kyeonghyeok Jin Ms. Genevieve C. Miller Disaster Management ˆ ` 2009.1.29 4:39 PM ˘ ` 2 ¿ ‚fiˆ •´ lp125 1200DPI 133LPI WMO/TD-No. 1476 World Meteorological Organization, 2009 ISBN 978-89-90564-89-4 93530 The right of publication in print, electronic and any other form and in any language is reserved by WMO. Short extracts from WMO publications may be reproduced without authorization, provided that the complete source is clearly indicated. Editorial correspon- dence and requests to publish, reproduce or translate this publication in part or in whole should be addressed to: Chairperson, Publications Board World Meteorological Organization (WMO) 7 bis, avenue de la Paix Tel.: +41 (0) 22 730 84 03 P.O. Box No. 2300 Fax: +41 (0) 22 730 80 40 CH-1211 Geneva 2, Switzerland E-mail: [email protected] NOTE The designations employed in WMO publications and the presentation of material in this publication do not imply the expression of any opinion whatsoever on the part of the Secretariat of WMO concerning the legal status of any country, territory, city or area, or of its authorities, or concerning the delimitation of its frontiers or boundaries. -

Typhoon Hagupit – Situation Report (20:30 Manila Time)
TYPHOON HAGUPIT NR. 1 7 DECEMBER 2014 Typhoon Hagupit – Situation Report (20:30 Manila Time) GENERAL INFORMATION - Typhoon Hagupit made landfall on Saturday 6 December at 9:15 pm in Dolores, Eastern Samar. After weakening to a Category 2 typhoon, Hagupit then made a second landfall in Cataingan, Masbate on Sunday 7 December. - Typhoon Hagupit has maintained its strength and is now (8:00 pm Manila Time) over the vicinity of Aroroy, Masbate. According to PAGASA’s weather bulletin issued today, 7 December at 18:00, the expected third landfall over Sibuyan Island will be between 02:00 – 04:00 in the morning tomorrow and will be associated with strong winds, storm surge and heavy to torrential rainfall. Hagupit is expected to exit the Philippine Area of Responsibility (PAR) on Thursday morning. - The typhoon is not as powerful as Typhoon Haiyan but Hagupit is moving slowly through the Philippines meaning prolonged rainfall and an increased likelihood of flooding and landslides. Currently the extent of damage is not yet clear. The authorities will send an assessment mission tomorrow to Region VIII where some municipalities in Eastern and Northern Samar are thought to have sustained heavier damage. Signal no. 1 has been issued in Manila, down from Signal no. 2 this morning Forecast Positions: - 24 hour (tomorrow afternoon): 60 km East of Calapan City, Oriental Mindoro or at 160 km South of Science Garden, Quezon City. - 48 hour (Tuesday afternoon): 170 km Southwest of Science Garden, Quezon City. - 72 hour (Wednesday afternoon): 400 km West of Science Garden, Quezon City. TYPHOON HAGUPIT NR. -

Sheared Deep Vortical Convection in Pre‐Depression Hagupit During TCS08 Michael M
GEOPHYSICAL RESEARCH LETTERS, VOL. 37, L06802, doi:10.1029/2009GL042313, 2010 Click Here for Full Article Sheared deep vortical convection in pre‐depression Hagupit during TCS08 Michael M. Bell1,2 and Michael T. Montgomery1,3 Received 28 December 2009; accepted 4 February 2010; published 17 March 2010. [1] Airborne Doppler radar observations from the recent (2008) that occurred during the TCS08 experiment, and Tropical Cyclone Structure 2008 field campaign in the suggested that the pre‐Nuri disturbance was of the easterly western North Pacific reveal the presence of deep, buoyant wave type with the preferred location for storm genesis near and vortical convective features within a vertically‐sheared, the center of the cat’s eye recirculation region that was readily westward‐moving pre‐depression disturbance that later apparent in the frame of reference moving with the wave developed into Typhoon Hagupit. On two consecutive disturbance. This work suggests that this new cyclogenesis days, the observations document tilted, vertically coherent model is applicable in easterly flow regimes and can prove precipitation, vorticity, and updraft structures in response to useful for tropical weather forecasting in the WPAC. It the complex shearing flows impinging on and occurring reaffirms also that easterly waves or other westward propa- within the disturbance near 18 north latitude. The observations gating disturbances are often important ingredients in the and analyses herein suggest that the low‐level circulation of formation process of typhoons [Chang, 1970; Reed and the pre‐depression disturbance was enhanced by the coupling Recker, 1971; Ritchie and Holland, 1999]. Although the of the low‐level vorticity and convergence in these deep Nuri study offers compelling support for the large‐scale convective structures on the meso‐gamma scale, consistent ingredients of this new tropical cyclogenesis model [Dunkerton with recent idealized studies using cloud‐representing et al., 2009], it leaves open important unanswered questions numerical weather prediction models. -

Upper Ocean Response to Typhoon Kalmaegi and Sarika in the South China Sea from Multiple-Satellite Observations and Numerical Simulations
remote sensing Article Upper Ocean Response to Typhoon Kalmaegi and Sarika in the South China Sea from Multiple-Satellite Observations and Numerical Simulations Xinxin Yue 1, Biao Zhang 1,* ID , Guoqiang Liu 1,2, Xiaofeng Li 3 ID , Han Zhang 4 and Yijun He 1 ID 1 School of Marine Sciences, Nanjing University of Information Science and Technology, Nanjing 210044, China; [email protected] (X.Y.); [email protected] (G.L.); [email protected] (Y.H.) 2 Bedford Institute of Oceanography, Fisheries and Oceans, Dartmouth, NS B2Y 4A2, Canada 3 GST at National Oceanic and Atmospheric Administration (NOAA)/NESDIS, College Park, MD 20740-3818, USA; [email protected] 4 State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Hangzhou 310012, China; [email protected] * Correspondence: [email protected] Received: 12 December 2017; Accepted: 22 February 2018; Published: 24 February 2018 Abstract: We investigated ocean surface and subsurface physical responses to Typhoons Kalmaegi and Sarika in the South China Sea, utilizing synergistic multiple-satellite observations, in situ measurements, and numerical simulations. We found significant typhoon-induced sea surface cooling using satellite sea surface temperature (SST) observations and numerical model simulations. This cooling was mainly caused by vertical mixing and upwelling. The maximum amplitudes were 6 ◦C and 4.2 ◦C for Typhoons Kalmaegi and Sarika, respectively. For Typhoon Sarika, Argo temperature profile measurements showed that temperature response beneath the surface showed a three-layer vertical structure (decreasing-increasing-decreasing). Satellite salinity observations showed that the maximum increase of sea surface salinity (SSS) was 2.2 psu on the right side of Typhoon Sarika’s track, and the maximum decrease of SSS was 1.4 psu on the left. -
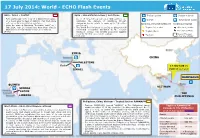
World - ECHO Flash Events
17 July 2014: World - ECHO Flash Events Gaza - Israel – Conflict Syria – Humanitarian access / assistance Tropical cyclone Disease outbreak Legend • Both parties agreed to respect a humanitarian pause • As of 16 July, UN agencies and NGO partners are Conflict Humanitarian access of 5 hours after 9 days of fighting. This must allow organizing the delivery of assistance through Cyclones Track points safe access for humanitarian assistance. designated border points to reach up to 2.9 million WIND_SPEEDTROPICAL CYCLONE INTENSITY TROPICAL CYCLONE • Since the start of Operation “Protective Edge” on 7 more people. July 2014, over 200 Palestinians have been killed in • The World Food Program is putting in place the UN Ï Tropical0.000000 Depression - 17.000000 Observed position Gaza and more than thousand have been injured. monitoring mechanism mandated in the relevant Tropical Storm Forecast position (ECHO) resolution. UNICEF has already positioned supplies Ï 17.000001 - 32.500000 ready for the first cross-border convoys. Area of Forecast Typhoon (ECHO, UN) Track Uncertainty Ï 32.500001 - 69.000000 Ï 69.000001 - 100.000000 SYRIA CHINA PALESTINE Gaza 17 July 6.00 UTC ISRAEL 138km/h sust. winds RAMMASUN GUINEA VIETNAM SIERRA LEONE THE LIBERIA PHILIPPINES Philippines, China, Vietnam – Tropical Cyclone RAMMASUN West Africa – Ebola Virus Disease outbreak • Typhoon RAMMASUN (named “GLENDA” in The Philippines) made Typhoon RAMMASUN landfall overnight 15-16 July (local time) in Albay and Quezon. On 17 Damage in The Philippines • As the number of Ebola cases and deaths in Guinea and, in particular, July, 6.00 UTC, its centre was located over the South China Sea, as of 17 July; source: NDRRMC Sierra Leone and Liberia continues to mount (964 cases and 603 approx. -

Initializing the WRF Model with Tropical Cyclone Real-Time Reports Using the Ensemble
Initializing the WRF Model with Tropical Cyclone Real-Time Reports using the Ensemble Kalman Filter Algorithm Tien Duc Du(1), Thanh Ngo-Duc(2), and Chanh Kieu(3)* (1)National Center for Hydro-Meteorological Forecasting, 8 Phao Dai Lang, Hanoi, Vietnam 1 (2)Department of Space and Aeronautics, University of Science and Technology of Hanoi, Vietnam 2 (3)Department of Earth and Atmospheric Sciences, Indiana University, Bloomington IN 47405, USA Revised: 18 April 2017 Submitted to Pure and Applied Geophysical Science Abbreviated title: Tropical Cyclone Ensemble Forecast Keywords: Tropical cyclones, ensemble Kalman filter, the WRF model, tropical cyclone vital, ensemble forecasting ____________________ *Corresponding author: Chanh Kieu, Atmospheric Program, GY428A Geological Building, Department of Earth and Atmospheric Sciences, Indiana University, Bloomington, IN 47405. Tel: 812-856-5704. Email: [email protected]. 1 1 Abstract 2 This study presents an approach to assimilate tropical cyclone (TC) real-time reports and the 3 University of Wisconsin-Cooperative Institute for Meteorological Satellite Studies (CIMSS) 4 Atmospheric Motion Vectors (AMV) data into the Weather Research and Forecasting (WRF) model 5 for TC forecast applications. Unlike current methods in which TC real-time reports are used to either 6 generate a bogus vortex or spin-up a model initial vortex, the proposed approach ingests the TC real- 7 time reports through blending a dynamically consistent synthetic vortex structure with the CIMSS- 8 AMV data. The blended dataset is then assimilated into the WRF initial condition, using the local 9 ensemble transform Kalman filter (LETKF) algorithm. Retrospective experiments for a number of 10 TC cases in the north Western Pacific basin during 2013-2014 demonstrate that this approach could 11 effectively increase both the TC circulation and enhance the large-scale environment that the TCs are 12 embedded in. -

Origin and Maintenance of the Long-Lasting, Outer Mesoscale Convective System in Typhoon Fengshen (2008)
2838 MONTHLY WEATHER REVIEW VOLUME 142 Origin and Maintenance of the Long-Lasting, Outer Mesoscale Convective System in Typhoon Fengshen (2008) BUO-FU CHEN Department of Atmospheric Sciences, National Taiwan University, Taipei, Taiwan RUSSELL L. ELSBERRY Department of Meteorology, Naval Postgraduate School, Monterey, California CHENG-SHANG LEE Department of Atmospheric Sciences, National Taiwan University, and Taiwan Typhoon and Flood Research Institute, National Applied Research Laboratories, Taipei, Taiwan (Manuscript received 27 January 2014, in final form 21 March 2014) ABSTRACT Outer mesoscale convective systems (OMCSs) are long-lasting, heavy rainfall events separate from the inner-core rainfall that have previously been shown to occur in 22% of western North Pacific tropical cyclones (TCs). Environmental conditions accompanying the development of 62 OMCSs are contrasted with the conditions in TCs that do not include an OMCS. The development, kinematic structure, and maintenance mechanisms of an OMCS that occurred to the southwest of Typhoon Fengshen (2008) are studied with Weather Research and Forecasting Model simulations. Quick Scatterometer (QuikSCAT) observations and the simulations indicate the low-level TC circulation was deflected around the Luzon terrain and caused an elongated, north–south moisture band to be displaced to the west such that the OMCS develops in the outer region of Fengshen rather than spiraling into the center. Strong northeasterly vertical wind shear contributed to frictional convergence in the boundary layer, and then the large moisture flux convergence in this moisture band led to the downstream development of the OMCS when the band interacted with the monsoon flow. As the OMCS developed in the region of low-level monsoon westerlies and midlevel northerlies associated with the outer circulation of Fengshen, the characteristic structure of a rear-fed inflow with a leading stratiform rain area in the cross-line direction (toward the south) was established. -

Hong Kong Observatory, 134A Nathan Road, Kowloon, Hong Kong
78 BAVI AUG : ,- HAISHEN JANGMI SEP AUG 6 KUJIRA MAYSAK SEP SEP HAGUPIT AUG DOLPHIN SEP /1 CHAN-HOM OCT TD.. MEKKHALA AUG TD.. AUG AUG ATSANI Hong Kong HIGOS NOV AUG DOLPHIN() 2012 SEP : 78 HAISHEN() 2010 NURI ,- /1 BAVI() 2008 SEP JUN JANGMI CHAN-HOM() 2014 NANGKA HIGOS(2007) VONGFONG AUG ()2005 OCT OCT AUG MAY HAGUPIT() 2004 + AUG SINLAKU AUG AUG TD.. JUL MEKKHALA VAMCO ()2006 6 NOV MAYSAK() 2009 AUG * + NANGKA() 2016 AUG TD.. KUJIRA() 2013 SAUDEL SINLAKU() 2003 OCT JUL 45 SEP NOUL OCT JUL GONI() 2019 SEP NURI(2002) ;< OCT JUN MOLAVE * OCT LINFA SAUDEL(2017) OCT 45 LINFA() 2015 OCT GONI OCT ;< NOV MOLAVE(2018) ETAU OCT NOV NOUL(2011) ETAU() 2021 SEP NOV VAMCO() 2022 ATSANI() 2020 NOV OCT KROVANH(2023) DEC KROVANH DEC VONGFONG(2001) MAY 二零二零年 熱帶氣旋 TROPICAL CYCLONES IN 2020 2 二零二一年七月出版 Published July 2021 香港天文台編製 香港九龍彌敦道134A Prepared by: Hong Kong Observatory, 134A Nathan Road, Kowloon, Hong Kong © 版權所有。未經香港天文台台長同意,不得翻印本刊物任何部分內容。 © Copyright reserved. No part of this publication may be reproduced without the permission of the Director of the Hong Kong Observatory. 知識產權公告 Intellectual Property Rights Notice All contents contained in this publication, 本刊物的所有內容,包括但不限於所有 including but not limited to all data, maps, 資料、地圖、文本、圖像、圖畫、圖片、 text, graphics, drawings, diagrams, 照片、影像,以及數據或其他資料的匯編 photographs, videos and compilation of data or other materials (the “Materials”) are (下稱「資料」),均受知識產權保護。資 subject to the intellectual property rights 料的知識產權由香港特別行政區政府 which are either owned by the Government of (下稱「政府」)擁有,或經資料的知識產 the Hong Kong Special Administrative Region (the “Government”) or have been licensed to 權擁有人授予政府,為本刊物預期的所 the Government by the intellectual property 有目的而處理該等資料。任何人如欲使 rights’ owner(s) of the Materials to deal with 用資料用作非商業用途,均須遵守《香港 such Materials for all the purposes contemplated in this publication.