An Efficient Mixed-Mode Representation of Sparse Tensors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
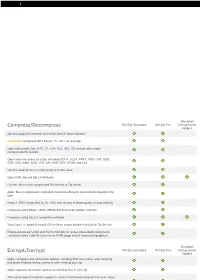
Compress/Decompress Encrypt/Decrypt
Windows Compress/Decompress WinZip Standard WinZip Pro Compressed Folders Zip and unzip files instantly with 64-bit, best-in-class software ENHANCED! Compress MP3 files by 15 - 20 % on average Open and extract Zipx, RAR, 7Z, LHA, BZ2, IMG, ISO and all other major compression file formats Open more files types as a Zip, including DOCX, XLSX, PPTX, XPS, ODT, ODS, ODP, ODG,WMZ, WSZ, YFS, XPI, XAP, CRX, EPUB, and C4Z Use the super picker to unzip locally or to the cloud Open CAB, Zip and Zip 2.0 Methods Convert other major compressed file formats to Zip format Apply 'Best Compression' method to maximize efficiency automatically based on file type Reduce JPEG image files by 20 - 25% with no loss of photo quality or data integrity Compress using BZip2, LZMA, PPMD and Enhanced Deflate methods Compress using Zip 2.0 compatible methods 'Auto Open' a zipped Microsoft Office file by simply double-clicking the Zip file icon Employ advanced 'Unzip and Try' functionality to review interrelated components contained within a Zip file (such as an HTML page and its associated graphics). Windows Encrypt/Decrypt WinZip Standard WinZip Pro Compressed Folders Apply encryption and conversion options, including PDF conversion, watermarking and photo resizing, before, during or after creating your zip Apply separate conversion options to individual files in your zip Take advantage of hardware support in certain Intel-based computers for even faster AES encryption Administrative lockdown of encryption methods and password policies Check 'Encrypt' to password protect your files using banking-level encryption and keep them completely secure Secure sensitive data with strong, FIPS-197 certified AES encryption (128- and 256- bit) Auto-wipe ('shred') temporarily extracted copies of encrypted files using the U.S. -

Winzip 12 Reviewer's Guide
Introducing WinZip® 12 WinZip® is the most trusted way to work with compressed files. No other compression utility is as easy to use or offers the comprehensive and productivity-enhancing approach that has made WinZip the gold standard for file-compression tools. With the new WinZip 12, you can quickly and securely zip and unzip files to conserve storage space, speed up e-mail transmission, and reduce download times. State-of-the-art file compression, strong AES encryption, compatibility with more compression formats, and new intuitive photo compression, make WinZip 12 the complete compression and archiving solution. Building on the favorite features of a worldwide base of several million users, WinZip 12 adds new features for image compression and management, support for new compression methods, improved compression performance, support for additional archive formats, and more. Users can work smarter, faster, and safer with WinZip 12. Who will benefit from WinZip® 12? The simple answer is anyone who uses a PC. Any PC user can benefit from the compression and encryption features in WinZip to protect data, save space, and reduce the time to transfer files on the Internet. There are, however, some PC users to whom WinZip is an even more valuable and essential tool. Digital photo enthusiasts: As the average file size of their digital photos increases, people are looking for ways to preserve storage space on their PCs. They have lots of photos, so they are always seeking better ways to manage them. Sharing their photos is also important, so they strive to simplify the process and reduce the time of e-mailing large numbers of images. -
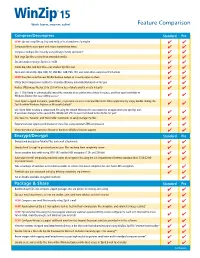
Winzip 15 Matrix 4.Cdr
15 Feature Comparison NEW! Compress/Decompress Standard Pro NEW! Zip and unzip files quickly and easily with a brand new zip engine Compress files to save space and reduce transmission times Compress multiple files instantly using WinZip's handy Zip button* Split large Zip files so they fit on removable media Zip and unzip very large Zip files (>4GB) Create Zip, LHA, and Zipx files—our smallest Zip files ever Open and extract Zip, Zipx, RAR, 7Z, LHA BZ2, CAB, IMG, ISO, and most other compressed file formats NEW! Drag files onto the new WinZip Desktop Gadget to instantly zip/unzip them Utilize 'Best Compression' method to maximize efficiency automatically based on file type Reduce JPEG image files by 20 to 25% with no loss of photo quality or data integrity Use '1-Click Unzip' to automatically extract the contents of an archive into a folder it creates, and then open that folder in Windows Explorer for easy editing access* 'Auto Open' a zipped document, spreadsheet, or presentation in its associated Microsoft Office application by simply double clicking the Zip file within Windows Explorer or Microsoft Outlook* Use 'Open With' to unzip a compressed file using the default Windows file association (or an application you specify), and, if you make changes to the opened file, WinZip will offer to save them back to the Zip file for you* Use 'Save As', 'Rename', and 'New Folder' commands to easily manage Zip files Experience faster zipping performance on most files using optional LZMA compression View international characters in filenames thanks to WinZip's Unicode support Encrypt/Decrypt Standard Pro Encrypt and decrypt confidential files and email attachments Simply check 'Encrypt' to password protect your files and keep them completely secure Secure sensitive data with strong, FIPS-197 certified AES encryption (128- and 256-bit) Auto-wipe ('shred') temporarily extracted copies of encrypted files using the U.S. -

About FOSS for Mac OS X (FREE)
Free and Open Source Software FREE for Mac OS X A selection of some of the best, yet totally free, software that’s available for the Mac, collected together on a single DVD… plus some bonus videos! Audio PrBoom Graphics First Person Shooter based on the Audacity original Doom. We’ve included Blender Simple sound recording and bonus IWADs from Freedoom. Fully integrated 3D graphics editing tool. creation suite allowing modeling, PySol Fan Club Edition animation, rendering, post- iPodDisk Collection of more than 1000 production, realtime interactive 3D Copy music off your iPod in the solitaire card games. There are and game creation and playback finder, just like a regular disk drive. games that use the 52 card with cross-platform compatibility - International Pattern deck, games all in one tidy, package! Games for the 78 card Tarock deck, eight and ten suit Ganjifa games, Seashore Aleph One Hanafuda games, Matrix games, Image editor that aims to serve the Engine for Bungie's free First Mahjongg games, and games for basic image editing needs of most Person Shooter series Marathon. an original hexadecimal-based computer users, but still has Play online, solo play with rich deck. features like gradients, textures and original story, many total Scorched 3D anti-aliasing for both text and conversions and thousands of brush strokes, as well as supporting Simple turn-based artillery game multiple layers and alpha channel maps. Includes Marathon, and also a real-time strategy game Marathon 2 & Marathon Infinity editing. It is based around the in which players can counter each GIMP's technology and uses the Armagetron Advanced others' weapons with other same native file format, but uses Multiplayer game in 3d that creative accessories, shields and Mac OS X native interface. -

Kafl: Hardware-Assisted Feedback Fuzzing for OS Kernels
kAFL: Hardware-Assisted Feedback Fuzzing for OS Kernels Sergej Schumilo1, Cornelius Aschermann1, Robert Gawlik1, Sebastian Schinzel2, Thorsten Holz1 1Ruhr-Universität Bochum, 2Münster University of Applied Sciences Motivation IJG jpeg libjpeg-turbo libpng libtiff mozjpeg PHP Mozilla Firefox Internet Explorer PCRE sqlite OpenSSL LibreOffice poppler freetype GnuTLS GnuPG PuTTY ntpd nginx bash tcpdump JavaScriptCore pdfium ffmpeg libmatroska libarchive ImageMagick BIND QEMU lcms Adobe Flash Oracle BerkeleyDB Android libstagefright iOS ImageIO FLAC audio library libsndfile less lesspipe strings file dpkg rcs systemd-resolved libyaml Info-Zip unzip libtasn1OpenBSD pfctl NetBSD bpf man mandocIDA Pro clamav libxml2glibc clang llvmnasm ctags mutt procmail fontconfig pdksh Qt wavpack OpenSSH redis lua-cmsgpack taglib privoxy perl libxmp radare2 SleuthKit fwknop X.Org exifprobe jhead capnproto Xerces-C metacam djvulibre exiv Linux btrfs Knot DNS curl wpa_supplicant Apple Safari libde265 dnsmasq libbpg lame libwmf uudecode MuPDF imlib2 libraw libbson libsass yara W3C tidy- html5 VLC FreeBSD syscons John the Ripper screen tmux mosh UPX indent openjpeg MMIX OpenMPT rxvt dhcpcd Mozilla NSS Nettle mbed TLS Linux netlink Linux ext4 Linux xfs botan expat Adobe Reader libav libical OpenBSD kernel collectd libidn MatrixSSL jasperMaraDNS w3m Xen OpenH232 irssi cmark OpenCV Malheur gstreamer Tor gdk-pixbuf audiofilezstd lz4 stb cJSON libpcre MySQL gnulib openexr libmad ettercap lrzip freetds Asterisk ytnefraptor mpg123 exempi libgmime pev v8 sed awk make -

Rule Base with Frequent Bit Pattern and Enhanced K-Medoid Algorithm for the Evaluation of Lossless Data Compression
Volume 3, No. 1, Jan-Feb 2012 ISSN No. 0976-5697 International Journal of Advanced Research in Computer Science RESEARCH PAPER Available Online at www.ijarcs.info Rule Base with Frequent Bit Pattern and Enhanced k-Medoid Algorithm for the Evaluation of Lossless Data Compression. Nishad P.M.* Dr. N. Nalayini Ph.D Scholar, Department Of Computer Science Associate professor, Department of computer science NGM NGM College, Pollachi, India College Pollachi, Coimbatore, India [email protected] [email protected] Abstract: This paper presents a study of various lossless compression algorithms; to test the performance and the ability of compression of each algorithm based on ten different parameters. For evaluation the compression ratios of each algorithm on different parameters are processed. To classify the algorithms based on the compression ratio, rule base is constructed to mine with frequent bit pattern to analyze the variations in various compression algorithms. Also, enhanced K- Medoid clustering is used to cluster the various data compression algorithms based on various parameters. The cluster falls dissentingly high to low after the enhancement. The framed rule base consists of 1,048,576 rules, which is used to evaluate the compression algorithm. Two hundred and eleven Compression algorithms are used for this study. The experimental result shows only few algorithm satisfies the range “High” for more number of parameters. Keywords: Lossless compression, parameters, compression ratio, rule mining, frequent bit pattern, K–Medoid, clustering. I. INTRODUCTION the maximum shows the peek compression ratio of algorithms on various parameters, for example 19.43 is the Data compression is a method of encoding rules that minimum compression ratio and the 76.84 is the maximum allows substantial reduction in the total number of bits to compression ratio for the parameter EXE shown in table-1 store or transmit a file. -

Preparing and Submitting Electronic Files for the IEEE 2000 Mobile Ad Hoc Networking and Computing Conference (Mobihoc)
Preparing and Submitting Electronic Files for the IEEE 2000 Mobile Ad Hoc Networking and Computing Conference (MobiHOC) Please read the detailed instructions that follow before you start, taking particular note of preferred fonts, formats, and delivery options. The quality of the finished product is largely dependent upon receiving your help at this stage of the publication process. Producing Your Paper Acceptable Formats Papers can be submitted in either PostScript (PS) or Portable Document Format (PDF) (see Generating PostScript and PDF Files). Using LaTeX Documents converted from the TeX typesetting language into PostScript or PDF files usually contain fixed-resolution bitmap fonts that do not print or display well on a variety of printer and computer screens. Although Adobe Acrobat Distiller will convert a PostScript language file with bitmapped fonts (level 3) into PDF, these fonts display slowly and do not render well on screen in the resulting PDF file. But, if you use Type 1 versions of the fonts you will get a compact file format that delivers the optimal font quality when used with any display screen, zoom mode, or printer resolution. Using Type 1 fonts with DVIPS The default behavior of Rokicki's DVIPS is to embed Type 3 bitmapped fonts. You need access to the Type 1 versions of the fonts you use in your documents in order to embed the font information (see Fonts). Type 1 versions of the Computer Modern fonts are available in the BaKoMa collection and from commercial type vendors. Before distributing files with embedded fonts, consult the license agreement for your font package. -

Insights from Operation Tomodachi Bilateral Coordination Action Team (BCAT) – Sendai
Insights from Operation Tomodachi Bilateral Coordination Action Team (BCAT) – Sendai COL Stephen Browne U.S. Army War College Fellow to Texas A&M University 1 (Source Photos: USARJ and JGSDF NEA Public Affairs) Agenda • Overview of the Great East Japan Earthquake (GEJE) and Tsunami Disaster • Operation Tomodachi Timeline • Joint Task Force–Tohoku and BCAT–Sendai Task Organization • BCAT-S Mission and Bilateral Coordination flow Structure • Key Lessons Learned • Conclusion 2 Overview – Earthquake and Tsunami Earthquake • 11 MAR, 1446 - 9.0 earthquake along Japan coast 230 miles NE of Tokyo • 3,970 roads, Pacific Coast and JR Railways completely disrupted • Sea Ports, Roads, and Rail Closed • Affected coastline lowered up to 1 meter • 2011 - estimated Rebuild Cost: USD $309 Tsunami • Epicenter offshore 65 miles east of Sendai • Tsunami damage fare more severe than earthquake • Wave height varied; up to 115ft • Affected over 420 miles of coastline 3 (Source: (1) USARJ CG Tomodachi Brief; (2) JTF-TH Brief to CODEL Levin/Webb/Inouye, CJCS, and LTG Wiercisnki;) Operational Timeline 01 1700 MAY - JFLCC repositioning complete & posture for future operations / support 26 APR- Begin JFLCC reposition OPs 08 APR- JLTF 10 established in Ishinomaki 07 APR- TOA between III MEF and USARJ; USARJ assumes JFLCC Operations 06 APR- LTF 35 moves to Ishinomaki Tomorrow Business Town 25 MAR- USARJ executes Voluntary Departure 21 MAR - LTF 35 deploys to Sendai Airport 15 MAR – Bilateral Coordination Action Team Stands Up – Sendai 14 MAR - III MEF designated as -

Software Requirements Specification
Software Requirements Specification for PeaZip Requirements for version 2.7.1 Prepared by Liles Athanasios-Alexandros Software Engineering , AUTH 12/19/2009 Software Requirements Specification for PeaZip Page ii Table of Contents Table of Contents.......................................................................................................... ii 1. Introduction.............................................................................................................. 1 1.1 Purpose ........................................................................................................................1 1.2 Document Conventions.................................................................................................1 1.3 Intended Audience and Reading Suggestions...............................................................1 1.4 Project Scope ...............................................................................................................1 1.5 References ...................................................................................................................2 2. Overall Description .................................................................................................. 3 2.1 Product Perspective......................................................................................................3 2.2 Product Features ..........................................................................................................4 2.3 User Classes and Characteristics .................................................................................5 -

Metadefender Core V4.10.1
MetaDefender Core v4.10.1 © 2018 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 13 Key Features of Metadefender Core 14 1. Quick Start with Metadefender Core 15 1.1. Installation 15 Installing Metadefender Core on Ubuntu or Debian computers 15 Installing Metadefender Core on Red Hat Enterprise Linux or CentOS computers 15 Installing Metadefender Core on Windows computers 16 1.2. License Activation 16 1.3. Scan Files with Metadefender Core 17 2. Installing or Upgrading Metadefender Core 18 2.1. Recommended System Requirements 18 System Requirements For Server 18 Browser Requirements for the Metadefender Core Management Console 20 2.2. Installing Metadefender Core 20 Installation 20 Installation notes 21 2.2.1. Installing Metadefender Core using command line 21 2.2.2. Installing Metadefender Core using the Install Wizard 23 2.3. Upgrading MetaDefender Core 23 Upgrading from MetaDefender Core 3.x 23 Upgrading from MetaDefender Core 4.x 23 2.4. Metadefender Core Licensing 24 2.4.1. Activating Metadefender Core Licenses 24 2.4.2. Checking Your Metadefender Core License 30 2.5. Performance and Load Estimation 31 What to know before reading the results: Some factors that affect performance 31 How test results are calculated 32 Test Reports 32 Performance Report - Multi-Scanning On Linux 32 Performance Report - Multi-Scanning On Windows 36 2.6. Special installation options 41 Use RAMDISK for the tempdirectory 41 3. -

Virtualizing the CIC Floppy Disk Project: an Experiment in Preservation Using Emulation Geoffrey Brown Indiana University Department of Computer Science
Virtualizing the CIC Floppy Disk Project: An Experiment in PreservaTion Using Emulation Geoffrey Brown Indiana University Department of Computer Science Issues We are Trying To Solve Documents in FDP (for example) require obsolete applications and operating systems Installing documents to access them requires specialized expertise These problems generalize to SUDOC documents on CD-ROM 3 7.8"3&8)*5&1"1&3 7JSUVBMJ[BUJPO0WFSWJFX *OUSPEVDUJPO 7JSUVBMJ[BUJPOJOB/VUTIFMM "NPOHUIFMFBEJOHCVTJOFTTDIBMMFOHFTDPOGSPOUJOH$*0TBOE 4JNQMZQVU WJSUVBMJ[BUJPOJTBOJEFBXIPTFUJNFIBTDPNF *5NBOBHFSTUPEBZBSFDPTUFGGFDUJWFVUJMJ[BUJPOPG*5JOGSBTUSVD 5IFUFSNWJSUVBMJ[BUJPOCSPBEMZEFTDSJCFTUIFTFQBSBUJPOPGB UVSFSFTQPOTJWFOFTTJOTVQQPSUJOHOFXCVTJOFTTJOJUJBUJWFT SFTPVSDFPSSFRVFTUGPSBTFSWJDFGSPNUIFVOEFSMZJOHQIZTJDBM BOEGMFYJCJMJUZJOBEBQUJOHUPPSHBOJ[BUJPOBMDIBOHFT%SJWJOH EFMJWFSZPGUIBUTFSWJDF8JUIWJSUVBMNFNPSZ GPSFYBNQMF BOBEEJUJPOBMTFOTFPGVSHFODZJTUIFDPOUJOVFEDMJNBUFPG*5 DPNQVUFSTPGUXBSFHBJOTBDDFTTUPNPSFNFNPSZUIBOJT CVEHFUDPOTUSBJOUTBOENPSFTUSJOHFOUSFHVMBUPSZSFRVJSFNFOUT QIZTJDBMMZJOTUBMMFE WJBUIFCBDLHSPVOETXBQQJOHPGEBUBUP 7JSUVBMJ[BUJPOJTBGVOEBNFOUBMUFDIOPMPHJDBMJOOPWBUJPOUIBU EJTLTUPSBHF4JNJMBSMZ WJSUVBMJ[BUJPOUFDIOJRVFTDBOCFBQQMJFE BMMPXTTLJMMFE*5NBOBHFSTUPEFQMPZDSFBUJWFTPMVUJPOTUPTVDI UPPUIFS*5JOGSBTUSVDUVSFMBZFSTJODMVEJOHOFUXPSLT TUPSBHF CVTJOFTTDIBMMFOHFT MBQUPQPSTFSWFSIBSEXBSF PQFSBUJOHTZTUFNTBOEBQQMJDBUJPOT 5IJTCMFOEPGWJSUVBMJ[BUJPOUFDIOPMPHJFTPSWJSUVBMJOGSBTUSVD UVSFQSPWJEFTBMBZFSPGBCTUSBDUJPOCFUXFFODPNQVUJOH TUPSBHFBOEOFUXPSLJOHIBSEXBSF BOEUIFBQQMJDBUJPOTSVOOJOH -

Software & Tools
TUGboat, Volume 19 (1998), No. 1 11 Software & Tools The future of AmiWeb2c Andreas Scherer Dear Amigicians, It is with great pleasure that I announce the avail ability of the latest, last, and final update of “Ami Web2c 2.1”, the Amiga port of the famous Web2c system (version 7.2) of “TEX and friends” (see http: //www.tug.org/web2c.html). This final release will hopefully fix all the bugs reported to me over the past year and it introduces a lot of new stuff not present in earlier versions. Three major resources for “AmiWeb2c” are CTAN:/systems/amiga/amiweb2c/. This is the • reference distribution of AmiWeb2c 2.1 on the “Comprehensive TEX Archive Network”. Aminet:/text/tex/. Identical in contents, but • packed in .lha instead of in .tar.gz format, this distribution is part of the “Aminet”, the world’s largest collection of free software tar geted to a single computer system. http://www.tug.org/texlive.html. A fully • integrated and ready-to-run installation of the Amiga binaries in the general Web2c setup is shipped with edition 3 of the “TEXLiveCD”. As pointed out in the closing remarks of the documentation coming with AmiWeb2c 2.1, I must now abandon the Amiga. Having served the TEX and Amiga community for several years by provid ing ports of, at first, standalone METAFONT and, since 1993, ever more complete TEX systems for the Amiga, the decision to step down as maintainer of AmiWeb2c was not easy to make. However, my professional career does not leave as much time as would be required to keep up with the many inter esting developments in the TEXnical field.