Multi-Task Learning Models for Functional Data and Application to the Prediction of Sports Performances Arthur Leroy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Henri Matisse, Textile Artist by Susanna Marie Kuehl
HENRI MATISSE, TEXTILE ARTIST COSTUMES DESIGNED FOR THE BALLETS RUSSES PRODUCTION OF LE CHANT DU ROSSIGNOL, 1919–1920 Susanna Marie Kuehl Submitted in partial fulfillment of the requirements for the degree Master of Arts in the History of Decorative Arts Masters Program in the History of Decorative Arts The Smithsonian Associates and Corcoran College of Art + Design 2011 ©2011 Susanna Marie Kuehl All Rights Reserved To Marie Muelle and the anonymous fabricators of Le Chant du Rossignol TABLE OF CONTENTS Page Acknowledgements . ii List of Figures . iv Chapter One: Introduction: The Costumes as Matisse’s ‘Best Spokesman . 1 Chapter Two: Where Matisse’s Art Meets Textiles, Dance, Music, and Theater . 15 Chapter Three: Expression through Color, Movement in a Line, and Abstraction as Decoration . 41 Chapter Four: Matisse’s Interpretation of the Orient . 65 Chapter Five: Conclusion: The Textile Continuum . 92 Appendices . 106 Notes . 113 Bibliography . 134 Figures . 142 i ACKNOWLEDGEMENTS As in all scholarly projects, it is the work of not just one person, but the support of many. Just as Matisse created alongside Diaghilev, Stravinsky, Massine, and Muelle, there are numerous players that contributed to this thesis. First and foremost, I want to thank my thesis advisor Dr. Heidi Näsström Evans for her continual commitment to this project and her knowledgeable guidance from its conception to completion. Julia Burke, Textile Conservator at the National Gallery of Art in Washington DC, was instrumental to gaining not only access to the costumes for observation and photography, but her energetic devotion and expertise in the subject of textiles within the realm of fine arts served as an immeasurable inspiration. -

National Chapter to Close Sigma N U House
National chapter to close Sigma Nu house By DAVE PALOMBI AND CAROLYN PETER Brothers required to reapply; fraternity to be reorganized "deteriorating situation over Sigma Nu fraternity has the last five or six years." been closed until at least next blem in the past will be read tional chapter is closing the receive first priority, ac Representatives from fall by their national chapter, mitted, he said. house, the fraternity can't ap cording to David Butler, Sigma Nu's national chapter, reported Stuart Sharkey, vice The procedure will be "ex peal the decision through the •director of Housing and their alumni chapter and president for Student Affairs. tremely selective," Allenby university. Residence Life. university administrators added. met last week to discuss the The house is closing at the The decision to reopen, Currently there are no There should, however, be future of the fraternity. end of this semester so that a · however, "will not be made plans for anyone to occupy enough housing to ac Sigma Nu National and the reorganization process can until Sigma Nu National and the house next semester, comodate everyone wanting a alumni chapter expressed take place, according to Ed the alumni chapter submit a Sharkey said. Housing and room, said Edward Spencer, concern over what was hap ward Allenby, a member of plan," Sharkey said. Residence Life might decide associate director for ad pening in the fraternity, and Sigma Nu's alumni chapter. Sometime next semester to use the house if necessary. ministration of Housing and jointly decided that some ac Sigma Nu National plans to The Sigma Nu house is the Residence Life. -

The Gaming Table, Its Votaries and Victims Volume #2
The Gaming Table, Its Votaries and Victims Volume #2 Andrew Steinmetz ******The Project Gutenberg Etext of Andrew Steinmetz's******** *********The Gaming Table: Its Votaries and Victims*********** Volume #2 #2 in our series by Andrew Steinmetz Copyright laws are changing all over the world, be sure to check the copyright laws for your country before posting these files!! Please take a look at the important information in this header. We encourage you to keep this file on your own disk, keeping an electronic path open for the next readers. Do not remove this. **Welcome To The World of Free Plain Vanilla Electronic Texts** **Etexts Readable By Both Humans and By Computers, Since 1971** *These Etexts Prepared By Hundreds of Volunteers and Donations* Information on contacting Project Gutenberg to get Etexts, and further information is included below. We need your donations. The Gaming Table, Its Votaries and Victims Volume #2 by Andrew Steinmetz May, 1996 [Etext #531] ******The Project Gutenberg Etext of Andrew Steinmetz's******** *********The Gaming Table: Its Votaries and Victims*********** *****This file should be named tgamt210.txt or tgamt210.zip****** Corrected EDITIONS of our etexts get a new NUMBER, tgamt211.txt. VERSIONS based on separate sources get new LETTER, tgamt210a.txt We are now trying to release all our books one month in advance of the official release dates, for time for better editing. Please note: neither this list nor its contents are final till midnight of the last day of the month of any such announcement. The official release date of all Project Gutenberg Etexts is at Midnight, Central Time, of the last day of the stated month. -

\0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3
... \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 x 1 Kampf ... \0-9\1, 2, 3 ... \0-9\1,000,000 ... \0-9\10 Pin ... \0-9\10... Knockout! ... \0-9\100 Meter Dash ... \0-9\100 Mile Race ... \0-9\100,000 Pyramid, The ... \0-9\1000 Miglia Volume I - 1927-1933 ... \0-9\1000 Miler ... \0-9\1000 Miler v2.0 ... \0-9\1000 Miles ... \0-9\10000 Meters ... \0-9\10-Pin Bowling ... \0-9\10th Frame_001 ... \0-9\10th Frame_002 ... \0-9\1-3-5-7 ... \0-9\14-15 Puzzle, The ... \0-9\15 Pietnastka ... \0-9\15 Solitaire ... \0-9\15-Puzzle, The ... \0-9\17 und 04 ... \0-9\17 und 4 ... \0-9\17+4_001 ... \0-9\17+4_002 ... \0-9\17+4_003 ... \0-9\17+4_004 ... \0-9\1789 ... \0-9\18 Uhren ... \0-9\180 ... \0-9\19 Part One - Boot Camp ... \0-9\1942_001 ... \0-9\1942_002 ... \0-9\1942_003 ... \0-9\1943 - One Year After ... \0-9\1943 - The Battle of Midway ... \0-9\1944 ... \0-9\1948 ... \0-9\1985 ... \0-9\1985 - The Day After ... \0-9\1991 World Cup Knockout, The ... \0-9\1994 - Ten Years After ... \0-9\1st Division Manager ... \0-9\2 Worms War ... \0-9\20 Tons ... \0-9\20.000 Meilen unter dem Meer ... \0-9\2001 ... \0-9\2010 ... \0-9\21 ... \0-9\2112 - The Battle for Planet Earth ... \0-9\221B Baker Street ... \0-9\23 Matches .. -

Reminiscences of Captain Gronow
Reminiscences of Captain Gronow Captain Rees Howell Gronow Reminiscences of Captain Gronow Table of Contents Reminiscences of Captain Gronow..........................................................................................................................1 Captain Rees Howell Gronow........................................................................................................................1 A FEW WORDS TO THE READER............................................................................................................3 MY ENTRANCE INTO THE ARMY...........................................................................................................4 DEPARTURE FOR AND ARRIVAL IN SPAIN.........................................................................................4 THE UNIFORM AND BEARING OF THE FRENCH SOLDIER..............................................................5 MAJOR−GENERAL STEWART AND LORD WELLINGTON................................................................5 ST. JEAN DE LUZ........................................................................................................................................6 FOOLHARDINESS.......................................................................................................................................7 DISCIPLINE..................................................................................................................................................8 SIR JOHN WATERS.....................................................................................................................................8 -

Catalog 019 Gambling WEB.Pdf
Public Auction #019 A Selection of Collectible and Unusual Gambling Memorabilia Including Rare Books; Early Playing Cards; Crooked Gambling Devices; Roulette & Gaming Wheels; Loaded Dice; Poker Chips; "Juice" Joints; Decorative Objects and Posters; Trade Stimulators; and More Auction Saturday, May 18th 2013 - 10:00 Am Exhibition May 15 - 17, 10:00 am - 5:00 pm Inquries [email protected] Phone: 773-472-1442 Potter & Potter Auctions, Inc. 3759 N. Ravenswood Ave. -Suite 121- Chicago, IL 60613 William "Canada Bill" Jones (?-1880) was a noted con man, riverboat gambler, and card sharp. He was described by his partner, George Devol as, "without doubt the greatest three-card monte sharp ever to work the boats — perhaps the greatest of them all." When told by Devol that a faro game was crooked, Jones supposedly replied: “Yeah, but it’s the only game in town.” 2 1 3 4 Books aBout GamBlinG, PlayinG Cards, lotteries, odds & ChanCe 1. Ackermann, Rudolf. Pictorial Cards in Thirteen Plates, Each 3. Anthony, Sir (Keresztfalvy, A. Vitez). The High Art of Containing Four Subjects, Partly Designed from the Subjoined Gambling. N.p., ca. 1937. Brown pictorial wraps. Square 12mo. Tale of Beatrice; or, The Fracas. London: R. Ackermann, 1819. Wraps chipped at extremities; good condition. Pp. [1-3], 4-28. Original front wrapper bound in at rear. Tooled 50/150 red morocco, spine banded and stamped in gold. 13 hand- colored plates. 4to. niCe CoPy. Rare. See Jessel 4. 4. Ashton, John. History of Gambling in England. Chicago: 1,000/1,500 Herbert S. Stone & Company, 1899. Red cloth with paper spine label. -
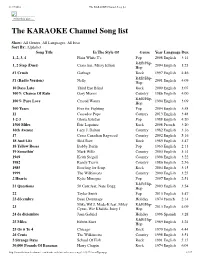
The KARAOKE Channel Song List
11/17/2016 The KARAOKE Channel Song list Print this List ... The KARAOKE Channel Song list Show: All Genres, All Languages, All Eras Sort By: Alphabet Song Title In The Style Of Genre Year Language Dur. 1, 2, 3, 4 Plain White T's Pop 2008 English 3:14 R&B/Hip- 1, 2 Step (Duet) Ciara feat. Missy Elliott 2004 English 3:23 Hop #1 Crush Garbage Rock 1997 English 4:46 R&B/Hip- #1 (Radio Version) Nelly 2001 English 4:09 Hop 10 Days Late Third Eye Blind Rock 2000 English 3:07 100% Chance Of Rain Gary Morris Country 1986 English 4:00 R&B/Hip- 100% Pure Love Crystal Waters 1994 English 3:09 Hop 100 Years Five for Fighting Pop 2004 English 3:58 11 Cassadee Pope Country 2013 English 3:48 1-2-3 Gloria Estefan Pop 1988 English 4:20 1500 Miles Éric Lapointe Rock 2008 French 3:20 16th Avenue Lacy J. Dalton Country 1982 English 3:16 17 Cross Canadian Ragweed Country 2002 English 5:16 18 And Life Skid Row Rock 1989 English 3:47 18 Yellow Roses Bobby Darin Pop 1963 English 2:13 19 Somethin' Mark Wills Country 2003 English 3:14 1969 Keith Stegall Country 1996 English 3:22 1982 Randy Travis Country 1986 English 2:56 1985 Bowling for Soup Rock 2004 English 3:15 1999 The Wilkinsons Country 2000 English 3:25 2 Hearts Kylie Minogue Pop 2007 English 2:51 R&B/Hip- 21 Questions 50 Cent feat. Nate Dogg 2003 English 3:54 Hop 22 Taylor Swift Pop 2013 English 3:47 23 décembre Beau Dommage Holiday 1974 French 2:14 Mike WiLL Made-It feat. -

Klondike Solitaire Kings Lataa Torrent Crack by Fitgirl
Klondike Solitaire Kings Lataa torrent crack by FitGirl Tietoja pelistä Famous Card game also known as Klondike. We kept the game true to the spirit of the classic Solitaire (also known as Klondike or Patience) Klondike Solitaire Kings features a beautiful custom designed card set in high resolution with 300+ levels, playing Patience on your desktop never looked this good! Features: Fun Addicting Games of Solitaire Classic 300+ levels Klondike Solitaire Draw 1 card Klondike Solitaire Draw 3 cards Winning Deals: Increase the challenge Vegas Cumulative: Keep your score rolling over Addicting, unique ways to play Customizable beautiful themes Daily challenges with different levels Clean and user-friendly menus Big and easy to see cards Auto-collect cards on completion Feature to UNDO moves Feature to use hints Standard or Vegas scoring How to Play Klondike Solitaire Klondike Solitaire is the most widely known solitaire game, popularised originally by being part of Windows 3.0 when it was released in 1990. Originally it was included to help teach people how to use a mouse correctly, but surely became one of the most popular little games to fill up a few minutes around the globe. It's quite relaxing and offers a good chance of winning with some basic playing techniques. Setting Up Klondike Solitaire Klondike Solitaire is played with a standard deck of 52 cards with all jokers removed. As you can see from the picture below, you must deal 7 columns of cards with the card at the bottom shown face up. The first column is one card (face up), the second is two cards with one card face up and the number of cards in each column increases by one until the final column is made of seven cards with the final card face up as with the other columns. -

Le Rouge Et Le Noir Devant La Critique
dans la solitude ; ingénue, rêveuse, distinguée par l’âme sans le savoir, ne jugeant pas son mari et adorant ses enfants, madame de Rênal Le Rouge et le Noir est d’abord choquée de l’idée qu’un petit prêtre sale et sournois va venir régenter ses devant la critique enfants et s’entreposer entre eux et leur 1 mère ; elle lutte un peu contre la vanité de son (1830-1894 ) mari, puis finit par se faire une raison. Heureusement le petit Julien, fils du vieux Par Xavier Bourdenet montagnard Sorel, et sur lequel le choix de et José-Luis Diaz M. de Rênal est tombé, n’est pas tout-à-fait ce que s’était représenté l’imagination de la jeune mère. Âgé de dix-huit à dix-neuf ans, faible en apparence, avec des traits irréguliers mais délicats, un nez aquilin, un œil vif et par 1830 : « Littérature », Le Globe, n° 247, moment farouche, pâle et pensif, le petit 27 octobre 1830. Julien, toujours grondé, souvent battu par son Le libraire Levavasseur doit publier ce père et par ses frères, n’a trouvé jusque-là livre sous peu de jours ; nous en parcourons d’asile et d’amitié que chez deux personnes, les feuilles avec tout l’attrait qu’inspire un d’abord un ancien chirurgien-major retiré qui ouvrage nouveau de M. de Stendal [sic] et lui a conté ses campagnes d’Italie, lui a appris notre curiosité est vivement amusée à chaque des bribes d’histoire, de latin et de chirurgie, page, comme dans tout ce que l’auteur a écrit l’a bercé du grand nom de Napoléon, et lui a de plus spirituel et de plus raffiné sur le cœur. -

Please Read the Note on P. 1163 Before Reading This Poem
MR SLUDGE, 'THE MEDIUM' 821 ;:1 Please read the note on p. 1163 before reading this poem. Mr Sludge, 'The Medium' Now, don't, sir! Don't expose me! Just this once! This was the firstand only time, I'll swear, - Look at me, - see, I kneel, - the only time, I swear, I ever cheated, -yes, by the soul !· Of Her who hears -(your sainted mother, sir!) All, except this last accident, was truth - This little kind of slip! - and even this, It was your own wine, sir, the good champagne, (I took it for Catawba, you're so kind) 10 Which put the follyin my head! 'Get up?' You still inflicton me that terrible face? You show no mercy? - Not forHer dear sake, The sainted spirit's, whose soft breath even now ....r�. ;if;.. -':,.,,P.·· .i:,-) :. ... ,•, �� -�: MR SLUDGE, 'THE MEDIUM' 822 DRAMA TIS PERSONAE 823 A rap or tip! What bit of paper's here? Blows on my cheek - (don't you feel something, sir?) ;i,·~ Suppose we take a pencil, let her write, You'll tell? ·'t r Make the least sign, she urges on her child Go tell, then! Who the devil cares , 50 Forgiveness? There now! Eh? Oh I 'Twas your foot, What such a rowdy chooses to ... r) And not a natural creak, sir? Aie-aie-aie! Please, sir! your thumbs are through my windpipe, sir I Answer, then! Ch-chi Ii Once, twice, thrice ... see, I'm waiting to say 'thrice!' l All to no use? No sort of hope for me? Well, sir, I hope you've done it now! 1'1 It's all to post to Greeley's newspaper? Oh Lord! I little thought, sir, yesterday, 20 When your departed mother spoke those words ;\: What? Ifl told you all about -

C:\Users\Gary\Documents
Gary & Myrna Lehrer’s Quarterly Illustrated Vintage Pen Catalog [email protected] Issue #85 - December 2017 See the Catalog in full color on the web site. For about a week you’ll need a password for access (be sure to also see what’s remaining from previous Catalogs). WEBSITE PASSWORD FOR CATALOG #85: (www.gopens.com): SANTA Catalog #85 Features: Featured: MIB items for your collection or for presents A Pelikan T111 Toledo and a Waterman 20 Two double-nibbed pens; a Colorado and a Zerollol Limited Editions, especially Montblanc Over 30 Manufacturers Over 275 Items Contact Information: Tel: (203) 389-5295 email: [email protected] Fax: (419) 730-1479 Call until 8:30 PM Eastern Time; Fax or email anytime We check our email often Subscription Expired: A (4) on your mailing label means your subscription has expired. “Internet Only” renewal is $10. “Hard Copy” Renewal is $25 US and $35 Foreign (see website for details). Received a sample copy? Don’t forget to subscribe ! Please see inside front page for abbreviations and other important information! Gary & Myrna Lehrer 16 Mulberry Road Woodbridge, CT 06525-1717 December 2017 - CATALOG #85 Here’s Some Other Important Information : GIFT CERTIFICATES : Available in any denomination. No extra cost! No expiration! CONSIGNMENT - PEN PURCHASES : We usually accept a small number of consignments. Ask about consignment rates (we reserve the right to turn down consignments), or see the website for details. We are also always looking to purchase one pen or entire collections. ABBREVIATIONS : Mint - No sign of use Fine - Used, parts show wear Near Mint - Slightest signs of use Good - Well used, imprints may be almost Excellent - Imprints good, writes well, looks great gone, plating wear Fine+ - One of the following: some brassing, Fair - A parts pen some darkening, or some wear ---------------------------------------------------------------------------------------------------------------------------------------- LF - Lever Filler HR - Hard Rubber PF - Plunger Filler (ie. -

Intendd for Both
A DOCUMENT RESUME ED 040 874 SE 008 968 AUTHOR Schaaf, WilliamL. TITLE A Bibli6graphy of RecreationalMathematics, Volume INSTITUTION National Council 2. of Teachers ofMathematics, Inc., Washington, D.C. PUB DATE 70 NOTE 20ap. AVAILABLE FROM National Council of Teachers ofMathematics:, 1201 16th St., N.W., Washington, D.C.20036 ($4.00) EDRS PRICE EDRS Price ME-$1.00 HC Not DESCRIPTORS Available fromEDRS. *Annotated Bibliographies,*Literature Guides, Literature Reviews,*Mathematical Enrichment, *Mathematics Education,Reference Books ABSTRACT This book isa partially annotated books, articles bibliography of and periodicalsconcerned with puzzles, tricks, mathematicalgames, amusements, andparadoxes. Volume2 follows original monographwhich has an gone through threeeditions. Thepresent volume not onlybrings theliterature up to material which date but alsoincludes was omitted in Volume1. The book is the professionaland amateur intendd forboth mathematician. Thisguide canserve as a place to lookfor sourcematerials and will engaged in research. be helpful tostudents Many non-technicalreferences the laymaninterested in are included for mathematicsas a hobby. Oneuseful improvementover Volume 1 is that the number ofsubheadings has more than doubled. (FL) been 113, DEPARTMENT 01 KWH.EDUCATION & WELFARE OffICE 01 EDUCATION N- IN'S DOCUMENT HAS BEEN REPRODUCED EXACILY AS RECEIVEDFROM THE CO PERSON OR ORGANIZATION ORIGINATING IT POINTS Of VIEW OR OPINIONS STATED DO NOT NECESSARILY CD REPRESENT OFFICIAL OFFICE OfEDUCATION INt POSITION OR POLICY. C, C) W A BIBLIOGRAPHY OF recreational mathematics volume 2 Vicature- ligifitt.t. confiling of RECREATIONS F DIVERS KIND S7 VIZ. Numerical, 1Afironomical,I f Antomatical, GeometricallHorometrical, Mechanical,i1Cryptographical, i and Statical, Magnetical, [Htlorical. Publifhed to RecreateIngenious Spirits;andto induce them to make fartherlcruciny into tilde( and the like) Suut.tm2.